Routing Services in Smart Cities: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Eleni Boumpa
,
Vasileios Tsoukas
,
Vasileios Chioktour
,
Maria Kalafati
,
Georgios Spathoulas
,
Athanasios Kakarountas
,
Panagiotis Trivellas
,
Panagiotis Reklitis
,
George Malindretos

The vehicle routing problem (VRP) is a complex optimization problem, in which there exists a set of clients at various locations, each one with a shipment need, and a fleet of vehicles, departing from the central depot that shall optimally satisfy the needs of the clients. The aim of a typical VRP is to find out the optimal route to minimize the total costs. Furthermore, various factors affecting route planning, such as vehicle capacity, fuel consumption, traffic congestion, etc., have to be considered to accomplish the minimization of the total route costs.

  • vehicle routing problem
  • urban routing
  • smart cities

1. The Vehicle Routing Problem

The client’s need for the delivery process to be accomplished in a restricted time frame has led to the definition of the Vehicle Routing Problem with Time Windows (VRPTW), in which the clients should be served by the vehicles, in a certain time window of a day [1].
The vehicle’s fuel emissions are a significant concern in many research fields, including VRP. Thus, the Fuel Consumption Vehicle Routing Problem (FCVRP) focuses on the minimization of the overall vehicle consumption and emission in the planning of a route [2]. The green VRP variant is focused on including both the minimum distance and the CO2 emission in route planning [3].
Another factor that can decrease the overall costs of logistic companies, and therefore the costs of the delivery process is the design of the supply chain network in a better way. This process consists of a better establishment of the depots’ locations and a better firmness of serving clients from the depots leading to the Location Routing Problem (LRP) [4]. Furthermore, a similar problem with the LRP is the Inventory Routing Problem (IRP), which emphasizes the minimization of distribution costs without affecting the client’s stock [5]. Lastly, the combination of LRP and IRP led to the implementation of Combined Location Routing and Inventory Problem (CLRIP) which minimize the overall costs by assigning the depots’ locations, arranging vehicles route planning, and defining the inventory policy based on the client’s needs [6].
However, in the reality, optimal route planning is not comprised of only one objective/factor but of combinations of those. Thus, the research community focused on the Multiobjective Routing Problems, which consider partial objectives/factors to generate the optimal route. An expansion of Capacitated Vehicle Routing Problem (CVRP) is Multiobjective Capacitated Vehicle Routing Problem (MOCVRP), in which two or three objectives are usually considered, such as distance, transportation time, or the number of the fleet of vehicles, to find the optimal route [7]. The Green Capacitated Vehicle Routing Problem (GCVRP) is classified in the same subcategory. The GCVRP focuses on green transportation by including the reduction of hazardous particles such as greenhouse gases, CO2, etc., and fuel consumption in a route [8][9]. The Multiobjective Vehicle Routing Problem with Time Windows (MOVRPTW) is a dilatation of VRPTW which takes into account the various aspects of the multiobjective problem of time window delivery [10]. Furthermore, the multiobjective extension of LRP is the Multiobjective Location Routing Problem (MOLRP) that considers at least transportation costs, lateness, and the number of vehicles combined with maximization of clients’ service quality [11][12].

2. Existing Routing Services

The scholars in [13] considered the employment of GAs to the basic VRP, in which customers are served from a single point. Vehicles are subject to a weight limit and, in some cases, to a distance limit, while only one vehicle is allowed to supply each customer.
Berger and Barkaoui propose a hybrid GA solving the VRPTW [14]. The proposed algorithm involves the simultaneous evolution of two solutions’ populations that face separate objectives with a relaxed time constraint. The first population evolves the solutions, to minimize the total travel distance, while the second population aims to minimize the transgression of the time constraint.
A novel hybrid GA for vehicle routing is proposed in [15]. The proposed solution finds the optimal path for the VRP, while simultaneously considering the vehicles’ heterogeneity, dual routes, and multiple depots.
In [16] a hybrid approach that combines a GA with the Dijkstra algorithm to solve a dynamic multi-objective problem is proposed. The proposed algorithm finds the solution simultaneously for three objective functions: route length, travel time, and ease of driving. In order to apply a GA to a traffic system, the scholars use Dijkstra’s algorithm to calculate the initial population of high-quality paths. On the initial population, the proposed approach applies a GA algorithm to generate the subsequent routes’ generations.
Moreover, a new approach of the ant colony algorithm to solve the VRP is presented in [17]. The main feature of this method is the hybridization of the solution construction mechanism of the ant colony algorithm, and the combination with a scatter search.
In [18] the proposed ant colony algorithm is used for the time windows-dependent routing problem (TDVRPTW). In this problem, a fleet of vehicles has to deliver goods to a set of customers, where the customers’ time interval constraints should be respected and the travel time between two points depends on the departure time.
In the SOUL project, information and communication technology are applied to the local food supply chain, such as the e-grocery supply chain [19]. The project’s architecture is made up of a central unit, a traffic handler service, a data broker layer, various hosted services, and third-party services, enabling technologies, sensors and other external data sources, and mobile devices. The aim of the proposed work is to enhance the efficiency and effectiveness of e-grocery activity in urban areas by incorporating a decision support system and a mobile application.

Identifying Key Points of the Existing Routing Services

Table 1 presents a coherent summary of whether each solution takes into account each one of the identified main features. The black dots in Table 1 indicate whether a feature applies to the service. These features are the following:
Table 1. Routing Services Features Comparison Table.
Project Time Window Green Routing Vehicle Capacity Fleet Management Transportation Costs Traffic Handler Travel Time/Distance
Baker & Ayechew [13] ∘ ∘ • ∘ ∘ ∘ •
Berger & Barkaoui [14] • ∘ ∘ ∘ • ∘ •
Montemanni et al. [20] ∘ ∘ • • • ∘ ∘
Wang et al. [21] • ∘ ∘ ∘ ∘ • •
Jeon et al. [15] ∘ ∘ • • ∘ ∘ •
Kanoh & Kenta [16] ∘ ∘ ∘ ∘ ∘ • •
Ho et al. [22] ∘ ∘ • • ∘ ∘ •
Falsini et al. [23] • • • • ∘ • •
Zhang & Tang [17] ∘ ∘ • ∘ • ∘ •
Tatomir et al. [24] ∘ ∘ ∘ ∘ ∘ • •
Yao et al. [25] ∘ ∘ ∘ ∘ • ∘ •
Cheeneebash & Nadal [26] • ∘ • • • ∘ •
Yu & Zhong [27] • ∘ • ∘ ∘ ∘ •
Balsiciro et al. [18] • ∘ • • ∘ • ∘
Jia et al. [28] ∘ ∘ • ∘ • ∘ •
Billhardt et al. [29] ∘ ∘ ∘ • • ∘ •
Anagnostopoulos et al. [30] ∘ • ∘ • • • •
Abousleiman & Rawashdeh [31] ∘ • ∘ ∘ ∘ ∘ •
Tadei et al.[19] • • ∘ • • • •
Natale et al. [32] ∘ • ∘ • • • ∘
Rivera et al. [33] ∘ ∘ • ∘ ∘ ∘ •
Hendawi et al. [34] ∘ ∘ ∘ ∘ ∘ • •
Qiu et al. [35] ∘ ∘ • • • ∘ ∘
Adnan & Abdulmuhsin [36] ∘ ∘ ∘ ∘ • ∘ •
Rout et al. [37] ∘ • ∘ ∘ ∘ • •
Akbarpour et al. [38] ∘ ∘ • • • ∘ •
Nagarajan et al. [39] ∘ ∘ ∘ ∘ • ∘ •
  • Time window: The requirement for delivery to happen under specific timing restrictions
  • Fleet management: The management of a number of vehicles and the optimization of the utilization of those.
  • Transportation cost: The combined economic cost of a route that consists of fuel cost, vehicle maintenance cost, and human labour cost.
  • Traffic handler: Taking into account traffic conditions for optimizing the route planning.
  • Travel time/distance: Minimising the route time and distance.
  • Green routing: Minimising the exhaust emissions.
  • Vehicle capacity: Take into consideration the capacity of a vehicle or fleet of vehicles for optimizing route planning.
Moreover, Table 1 shows the integration of the features in studied research routing approaches. The basic approach that is common throughout almost all cases is travel time/distance optimization. The main objective of VRP is identifying the fastest/shortest routes. It has to be noted though that there are cases where the proposed systems ignore this parameter and focus on other objectives, such as transportation costs [13][14][15][16][17][19][21][22][23][24][25][26][27][28][29][30][31][33][34][36][37][38][39].
The second most evident feature is transportation costs. In a simplistic approach, this metric can be assessed as directly connected to the travel distance. The actual transportation cost depends heavily on travel distance but is also related to other parameters such as the altitude variance along a route, the fuel type of the vehicle or the maintenance plan for the fleet. According to the problem set-up, it may be required to take into account one of the two aforementioned features or both. A route planning solution has to combine both and allow the user to set his preferences [14][17][19][20][25][26][28][29][30][32][35][36][38][39].
An interesting case is the integration of the fleet management feature. More than half of the proposed solutions do not take into account fleet management and are restricted to solving the problem of route planning either with a single vehicle or under a simplistic approach that the iteration of optimal route planning with a single vehicle for a pool of orders and a number of vehicles can efficiently solve the problem.
Another important feature that seems not to receive significant attention is the time window feature. When the routes refer to products that impose specific timing restrictions, either for preserving their quality or because the delivery time is critical for the application. Only seven of the discussed services take the timing window into account and this for sure presents a limitation in the current state of the art. 

3. Routing Services Incorporating Machine Learning Techniques

Machine Learning (ML) is the most popular technology used in addition to conventional algorithms, to improve the performance of the aforementioned algorithms. 

The objective of work [40] is to solve the CVRP using ML-based techniques. The scholars proposed the “Learn to Improve” (L2I), a learning-based solution for CVRP that excels Operation Research (OR) algorithms in terms of solving speed. Specifically, the scholars demonstrated a learning-based algorithm for the CVRP, proposing a framework capable of splitting heuristic operators into two different groups to accelerate the operation and concentrate Reinforcement Learning (RL) on those identified as improvement operators. Lastly, they presented an ensemble technique in which RL rules are taught simultaneously, yielding improved outcomes at the same computational cost.

Work [41] provides a solution to the Energy Minimizing Vehicle Routing Challenge (EMVRP), a problem that focuses on locating routes of vehicles that consume the lowest amount of energy when servicing a collection of cities or clients. The scholars offer an implementation of a genetic algorithm that is augmented by ML approaches to tweak its parameters in a subsequent phase. The strategy under discussion is the application of k-means clustering, which demonstrated that the identification of distinct data clusters has a substantial influence on enhancing the effectiveness of the utilized genetic algorithm.

In order to solve one of the most common problems encountered in the field of transportation and supply chain delivery, the CVRP, a research team used a recursive approach of the k-means clustering algorithm along with the Dijkstra shortest path algorithm [42]. The proposed solution divides into parts the CVRP to find the optimal route. Firstly, it takes into account the capacity of the fleet of vehicles to optimize the total route’s capacity; then the k-means algorithm, considering the travel time, distance travel, and vehicles’ capacity, is implemented; in the next step, the optimal capacity of vehicles is ensured; while in the last step, the Dijkstra’s algorithm finds the shortest route for the fleet of vehicles.

4. An Efficient Solution Regarding the VRP

On the basis of the aforementioned discoveries, it initiated the design of a framework capable of delivering an efficient solution for the VRP and its variants, including the CVRP and the GVRP. The proposed system considers all the stages of the logistics workflow, from the initial order placement through the delivery of the goods to the client. Initially, the set of delivery points is processed, and batches of close geographical locations of the delivery addresses are created dynamically by utilizing ML models. Subsequently, an ensemble scheme of various genetic algorithms is used to identify the optimal route for each one of those batches. Regarding the optimal route, the vehicles start from the same starting point, make exactly one stop at each client, and finally, return to the starting point. The aforementioned procedure considers the overall COx emissions, and the total distance travelled.

4.1. Experimental Results Regarding the Initial Stage of System’s Development

Regarding the initial stage of development, the first observations made were related to the percentage of routes that were successfully handled by the system, as well as the percentage of routes deemed more efficient in terms of distance travelled when compared to actual data.
Initial simulations showed that the proposed ensemble scheme was able to handle successfully (identify a route that complies with the VRP restrictions) the 74% of the routes, as displayed in Figure 1.
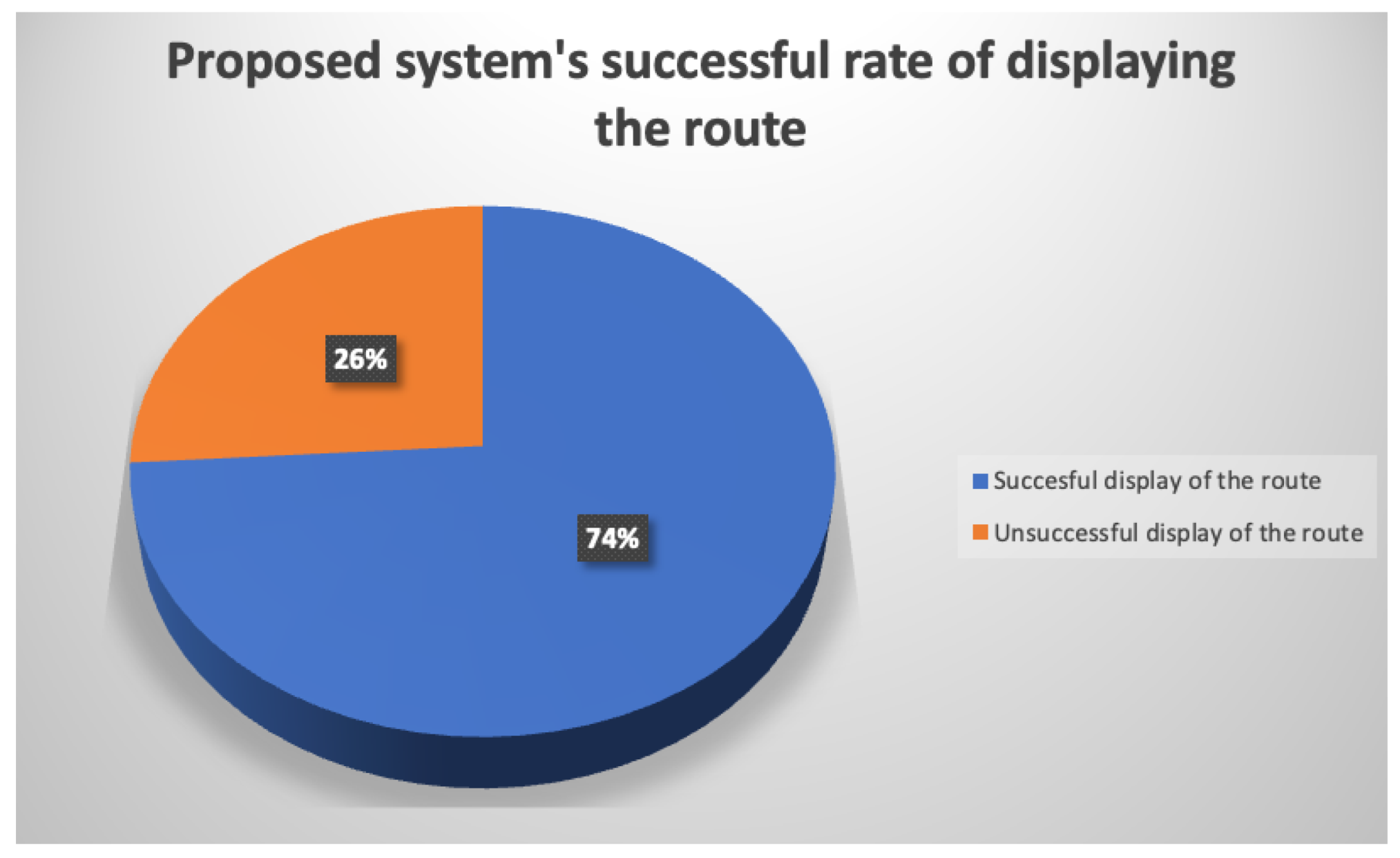
/media/item_content/202301/63d8cafd9cfb0analytics-02-00001-g002.png
Figure 1. Successful rate in regard to the display of the route from the proposed system.
Out of the routes that were successfully handled, 86% were deemed to be a better route recommendation in terms of total distance travelled, whereas only 14% of the displayed routes were unable to locate a more efficient solution. Figure 2 shows the percentage of the routes which achieved a more efficient route.
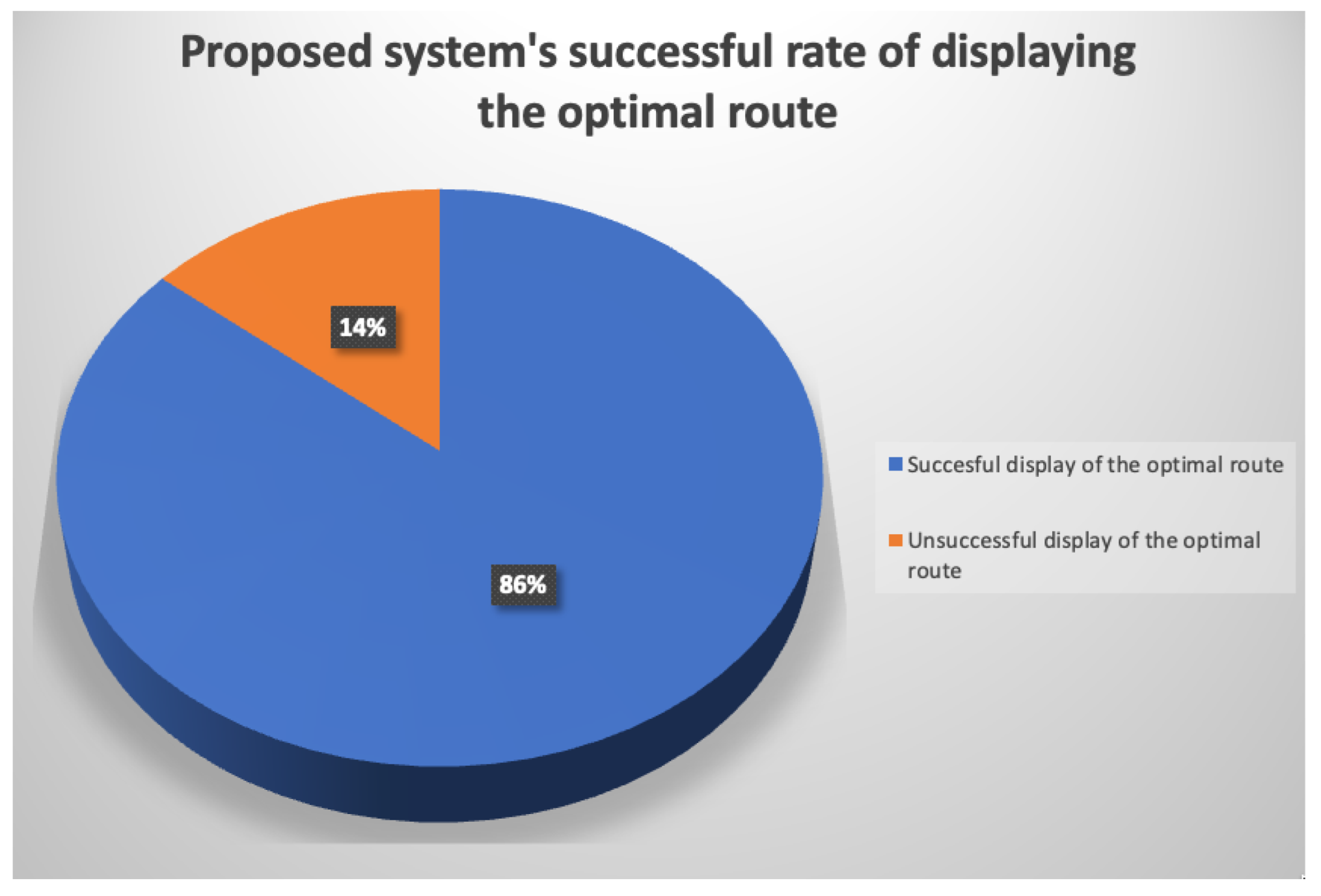
/media/item_content/202301/63d8cb13ecd13analytics-02-00001-g003.png
Figure 2. Successful rate in regard to the display of the optimal route from the proposed system.

4.2. Evaluation of the Routes Displayed by the System

For each starting point, a number of routes are included in the real-world data. Figure 3 depicts the minimum (orange) and maximum (blue) distance deviation values for the whole set of routes from each starting point for the proposed system. In comparison to the real conditions of Starting Point 5, a variance of 8517 meters emerges in this set of routes.
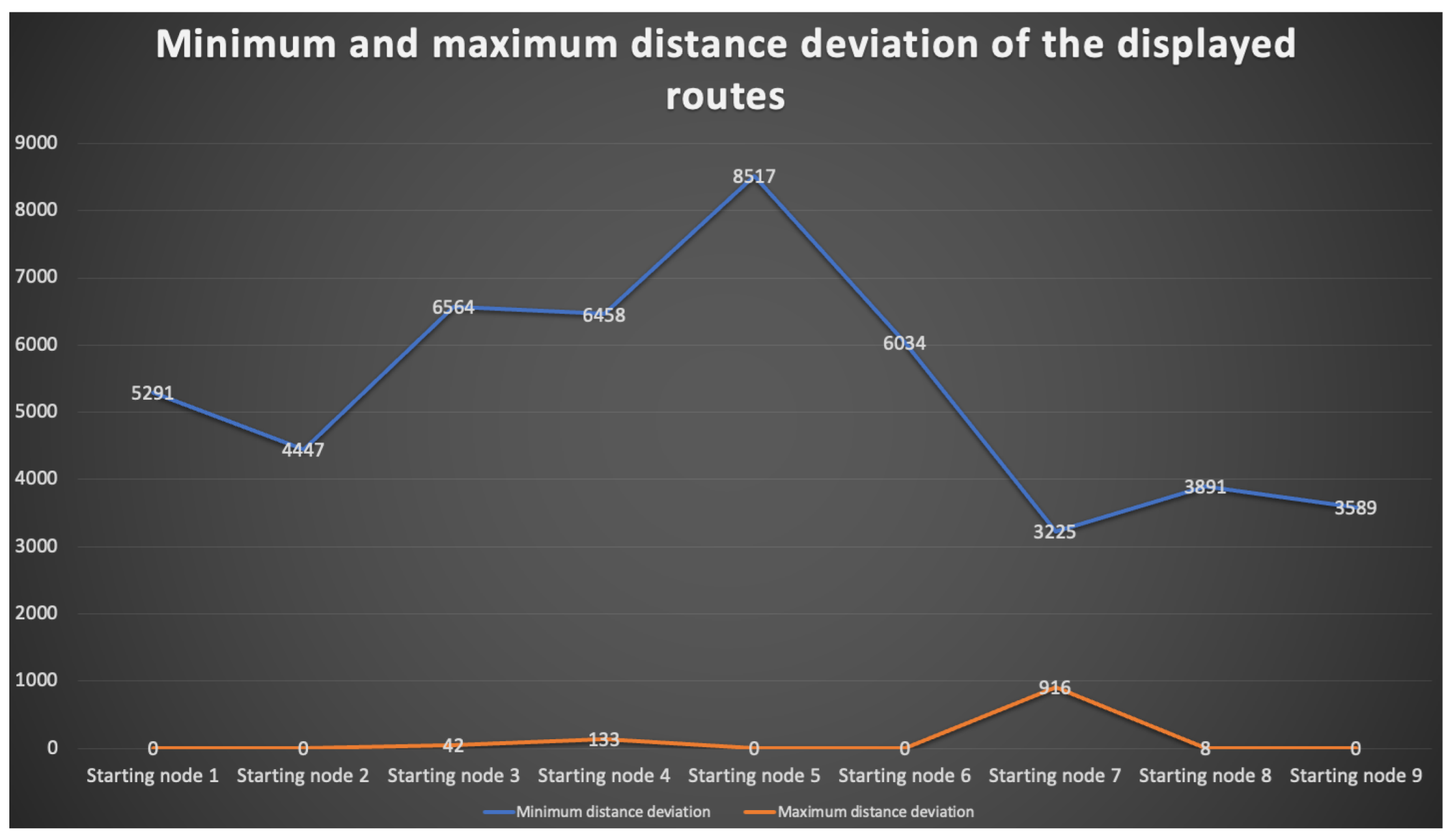
/media/item_content/202301/63d8cb363bb70analytics-02-00001-g004.png
Figure 3. Minimum and maximum time deviation of the displayed routes.
Similarly, in regard to the total time, Figure 4 depicts, with respect to the total time travelled, the minimum (orange) and maximum (blue) time deviations in the set of all routes from each beginning point, based on the proposed system, versus the actual conditions of a route. On a number of instances, the system requires a longer period of time to deliver orders than actual data.
/media/item_content/202301/63d8cb4894617analytics-02-00001-g005.png
Figure 4. Minimum and maximum distance deviation of the displayed routes.

This entry is adapted from the peer-reviewed paper 10.3390/analytics2010001

References

  1. El-Sherbeny, N.A. Vehicle routing with time windows: An overview of exact, heuristic and metaheuristic methods. J. King Saud-Univ.-Sci. 2010, 22, 123–131.
  2. Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431.
  3. Tiwari, A.; Chang, P.C. A block recombination approach to solve green vehicle routing problem. Int. J. Prod. Econ. 2015, 164, 379–387.
  4. Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17.
  5. Campbell, A.; Clarke, L.; Kleywegt, A.; Savelsbergh, M. The inventory routing problem. In Fleet Management and Logistics; Springer: Boston, MA, USA, 1998; pp. 95–113.
  6. Liu, S.C.; Lin, C.C. A heuristic method for the combined location routing and inventory problem. Int. J. Adv. Manuf. Technol. 2005, 26, 372–381.
  7. Murata, T.; Itai, R. Local search in two-fold EMO algorithm to enhance solution similarity for multi-objective vehicle routing problems. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Matsushima, Japan, 5–8 March 2007.
  8. Adiba, E.E.; Aahmed, E.A.; Youssef, B. The green capacitated vehicle routing problem: Optimizing of emissions of greenhouse gas. In Proceedings of the 2014 International Conference on Logistics Operations Management, Rabat, Morocco, 5–7 June 2014.
  9. Zhang, J.; Zhao, Y.; Xue, W.; Li, J. Vehicle routing problem with fuel consumption and carbon emission. Int. J. Prod. Econ. 2015, 170, 234–242.
  10. Min, H. A multiobjective vehicle routing problem with soft time windows: The case of a public library distribution system. Socio-Econ. Plan. Sci. 1991, 25, 179–188.
  11. Liu, H.; Wang, W.; Zhang, Q. Multi-objective location-routing problem of reverse logistics based on GRA with entropy weight. Grey Syst. Theory Appl. 2012, 2, 249–258.
  12. Lin, C.K.Y.; Kwok, R.C.W. Multi-objective metaheuristics for a location-routing problem with multiple use of vehicles on real data and simulated data. Eur. J. Oper. Res. 2006, 175, 1833–1849.
  13. Baker, B.M.; Ayechew, M. A genetic algorithm for the vehicle routing problem. Comput. Oper. Res. 2003, 30, 787–800.
  14. Berger, J.; Barkaoui, M. A parallel hybrid genetic algorithm for the vehicle routing problem with time windows. Comput. Oper. Res. 2004, 31, 2037–2053.
  15. Jeon, G.; Leep, H.R.; Shim, J.Y. A vehicle routing problem solved by using a hybrid genetic algorithm. Comput. Ind. Eng. 2007, 53, 680–692.
  16. Kanoh, H.; Hara, K. Hybrid genetic algorithm for dynamic multi-objective route planning with predicted traffic in a real-world road network. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, GA, USA, 12–16 July 2008.
  17. Zhang, X.; Tang, L. A new hybrid ant colony optimization algorithm for the vehicle routing problem. Pattern Recognit. Lett. 2009, 30, 848–855.
  18. Balseiro, S.R.; Loiseau, I.; Ramonet, J. An ant colony algorithm hybridized with insertion heuristics for the time dependent vehicle routing problem with time windows. Comput. Oper. Res. 2011, 38, 954–966.
  19. Tadei, R.; Fadda, E.; Gobbato, L.; Perboli, G.; Rosano, M. An ICT-based reference model for e-grocery in smart cities. In Proceedings of the International Conference on Smart Cities, Málaga, Spain, 15–17 June 2016.
  20. Montemanni, R.; Gambardella, L.M.; Rizzoli, A.E.; Donati, A.V. Ant colony system for a dynamic vehicle routing problem. J. Comb. Optim. 2005, 10, 327–343.
  21. Wang, J.Q.; Tong, X.N.; Li, Z.M. An improved evolutionary algorithm for dynamic vehicle routing problem with time windows. In Proceedings of the International Conference on Computational Science, Beijing China, 27–30 May 2007.
  22. Ho, W.; Ho, G.T.; Ji, P.; Lau, H.C. A hybrid genetic algorithm for the multi-depot vehicle routing problem. Eng. Appl. Artif. Intell. 2008, 21, 548–557.
  23. Falsini, D.; Fumarola, A.; Schiraldi, M.M. Sustainable trasportation systems: Dynamic routing optimization for a last-mile distribution fleet. In Proceedings of the Conference on Sustainable Development: The Role of Industrial Engineering, DIMEG Università di Bari, 2009.
  24. Tatomir, B.; Rothkrantz, L.J.; Suson, A.C. Travel time prediction for dynamic routing using ant based control. In Proceedings of the 2009 Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009.
  25. Yao, J.; Lin, C.; Xie, X.; Wang, A.J.; Hung, C.C. Path planning for virtual human motion using improved A* star algorithm. In Proceedings of the 2010 Seventh International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 12–14 April 2010.
  26. Cheeneebash, J.; Nadal, C. Using Tabu Search Heuristics in Solving the Vehicle Routing Problem with Time Windows: Application to a Mauritian Firm. Univ. Maurit. Res. J. 2010, 16, 448–471.
  27. Yu, B.; Yang, Z.Z. An ant colony optimization model: The period vehicle routing problem with time windows. Transp. Res. Part Logist. Transp. Rev. 2011, 47, 166–181.
  28. Jia, H.; Li, Y.; Dong, B.; Ya, H. An improved tabu search approach to vehicle routing problem. Procedia-Soc. Behav. Sci. 2013, 96, 1208–1217.
  29. Billhardt, H.; Fernández, A.; Lemus, L.; Lujak, M.; Osman, N.; Ossowski, S.; Sierra, C. Dynamic coordination in fleet management systems: Toward smart cyber fleets. IEEE Intell. Syst. 2014, 29, 70–76.
  30. Anagnostopoulos, T.; Kolomvatsos, K.; Anagnostopoulos, C.; Zaslavsky, A.; Hadjiefthymiades, S. Assessing dynamic models for high priority waste collection in smart cities. J. Syst. Softw. 2015, 110, 178–192.
  31. Abousleiman, R.; Rawashdeh, O. A Bellman-Ford approach to energy efficient routing of electric vehicles. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015.
  32. Natale, E.; Tufo, M.; Salvi, A. A fleet management service for smart cities: The S 2-move project. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016.
  33. Rivera, J.C.; Afsar, H.M.; Prins, C. Mathematical formulations and exact algorithm for the multitrip cumulative capacitated single-vehicle routing problem. Eur. J. Oper. Res. 2016, 249, 93–104.
  34. Hendawi, A.M.; Rustum, A.; Ahmadain, A.A.; Hazel, D.; Teredesai, A.; Oliver, D.; Ali, M.; Stankovic, J.A. Smart Personalized Routing for Smart Cities. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 1295–1306.
  35. Qiu, M.; Fu, Z.; Eglese, R.; Tang, Q. A Tabu Search algorithm for the vehicle routing problem with discrete split deliveries and pickups. Comput. Oper. Res. 2018, 100, 102–116.
  36. Adnan, S.; Abdulmuhsin, W. The multi-point delivery problem: Shortest Path Algorithm for Real Roads Network using Dijkstra. J. Phys. Conf. Ser. 2020, 1530, 012040.
  37. Rout, R.R.; Vemireddy, S.; Raul, S.K.; Somayajulu, D.V. Fuzzy logic-based emergency vehicle routing: An IoT system development for smart city applications. Comput. Electr. Eng. 2020, 88, 106839.
  38. Akbarpour, N.; Salehi-Amiri, A.; Hajiaghaei-Keshteli, M.; Oliva, D. An innovative waste management system in a smart city under stochastic optimization using vehicle routing problem. Soft Comput. 2021, 25, 6707–6727.
  39. Nagarajan, S.M.; Deverajan, G.G.; Chatterjee, P.; Alnumay, W.; Muthukumaran, V. Integration of IoT based routing process for food supply chain management in sustainable smart cities. Sustain. Cities Soc. 2022, 76, 103448.
  40. Lu, H.; Zhang, X.; Yang, S. A learning-based iterative method for solving vehicle routing problems. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019.
  41. Cooray, P.L.; Rupasinghe, T.D. Machine learning-based parameter tuned genetic algorithm for energy minimizing vehicle routing problem. J. Ind. Eng. 2017, 2017, 3019523.
  42. Moussa, H. Using recursive KMeans and Dijkstra algorithm to solve CVRP. arXiv 2021, arXiv:2102.00567.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback