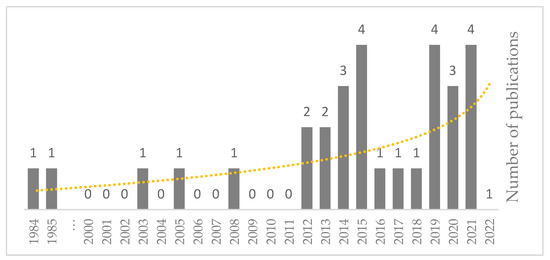
A year-wise analysis informs the reader about the progress research, and highlights the researchers’ interest in the subject. Figure 1 illustrates the number of published studies since 1984. There were some initiatives in 1984 and 1985, followed by three studies in 2003, 2005, and 2008. The main studies began in 2012, with the highest in 2015, 2019, and 2021 by four studies. Interestingly, as of September 2022, no studies have been registered. One reason for this low interest could be the huge uncertainties associated with mathematical modeling. Moreover, as mentioned earlier, the current mathematical models are not covering all reactions, and because this analysis is mainly based on mathematical models, it is challenging to interpret the results.

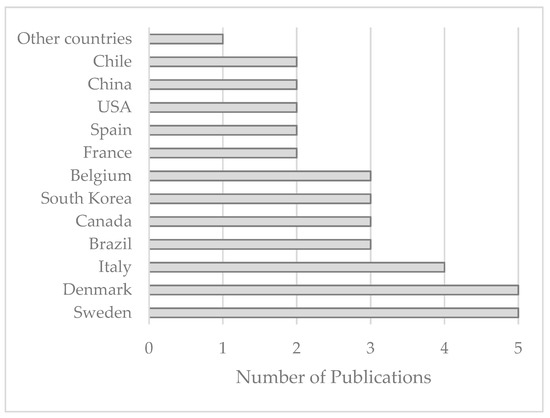
Analysis of the selected publications revealed that 23 countries contributed to this topic (1984–2022). As seen in Figure 2, the highest contribution belongs to Sweden and Denmark, with five studies (4 joint publications), followed by Italy, with four studies. Brazil, Canada, South Korea, and Belgium contributed to three publications. France, Spain, the USA, China, and Chile had two publications each. Eleven countries were involved in only one publication each, categorized under “Other Countries.” Norway, Romania, Australia, Russia, Finland, Iran, Lebanon, Saudi Arabia, the UK, France, South Africa, and Cuba belong to this category.

As discussed earlier, this entry considered all types of publications, excluding reports and gray literature. There are three types in the selected documents. Articles have the highest rank of 84%, conference papers have the second-highest rank of 13%, with four studies [39,40,41,42], and one thesis [43] makes up only 3%. Book chapters and, most importantly, reviews were not addressed in the 30 selected studies, which emphasizes the importance and lack of review studies on this topic.

In order to implement a model predictive control system for AD systems, Li et al. [61] developed linearized ADM1 (LADM) as a model predictive control for anaerobic digestion systems. Model input data from the lab-scale AD system was used for the sensitivity test. SA resulted that k_dis, k_{hyd_ch}, k_{m_ac}, K_{S_ac}, and Y_ac were the most influential parameters. Based on an anaerobic digestion model, Silva and De Bortoli [63] calculated the first-order sensitivity coefficients for a system of stiff nonlinear differential equations. As part of this approach, the auxiliary equations were used to calculate the sensitivity coefficients solved separately from the model equations, using the same numerical approximations and time steps used to calculate the model solution using the 4th-order Rosenbrock method [70]. Based on the results, they could determine the importance of each reaction for each species involved in the model. Fatolahi et al. [44] calibrated ADM1 incorporated into Matlab/Simulink to simulate a mesophilic lab-scale reactor fed with the organic fraction of municipal solid waste. A sensitivity index based on Shannon entropy was used to determine five parameters as indicators: biogas flow, methane flow, pH, effluent COD, and ammonia concentration. Shannon entropy [71] refers to a measure of the uncertainty regarding the occurrence of a given event, given partial information about the system. According to the results, all other indicators’ parameters could be covered by the parameters of the biogas flow indicator with an entropy greater than 0.2 dB. In addition, genetic algorithms were used to estimate 13 critical kinetic parameters, including the maximum specific uptake rate of sugar, propionate, acetate, etc. Based on a techno-economic approach, Fuess and Ziait [57] identified the key factors affecting the economic performance of sugarcane biorefineries’ AD of vinasses.

Macleod et al. [59] determined the models’ quantitative sensitivities using factorial design. A factorial design allows the effects of a factor to be assessed at several levels of the other factors, enabling valid conclusions to be drawn over a wide range of variables [72]. The retention time had the greatest impact on total solids removal and volatile solids removal, and biogas was greatly influenced by loading rate and temperature. There was a high degree of precision in the regression model fitted to the experimental data, indicating that small reactors were as sensitive to changes in loading, retention time, and temperature as full-scale digesters. Benbelkacem et al. [47] performed a sensitivity analysis on ADM1 to investigate how biogas production was affected by K_La and K_mX. Atallah et al. [51] conducted an LSA on ADM1 based on the two sets of digester data to optimize parameters based on five performance indicators: methane generation, pH, acetate, total COD, and ammonia. It was concluded that at one end of the simulated range, some parameters are highly sensitive. However, on the other end, they are less sensitive. In order to simulate the operation of continuous digesters fed at different HRTs, Souza et al. [52] evaluated the feasibility of using biochemical methane potential (BMP) tests data to calibrate ADM1. Based on data from BMP tests, a sensitivity analysis was conducted to determine the most sensitive ADM1 parameters to be calibrated. The “fminsearch” function from MATLAB® (Mathworks, Natick, MA, USA) was used for calibrating the differences between experimental and simulated values. As a result, asymmetric characteristics were observed for k_dis, k_hydch, k_hydpr, and k_hydli when the parameters were varied at low levels. At low ranges, kmac also showed a high degree of sensitivity. In order to establish the basis for the appropriate application of the ADM1, Jeong et al. [53] developed a model for the serum bottle test that allows for a comparison of stoichiometric and kinetic parameters with the components. The results showed that the product yield on the substrate had a high sensitivity to model components, with methane concentration being the most sensitive. Although Monod’s maximum specific uptake rate was strongly associated with biomass concentration, individual values could not be determined.

Pinto et al. [56] identified the most sensitive parameters affecting the economic viability of investments for generating electrical energy through anaerobic bio-digestion of vinasses. Several strategically selected variables were subjected to a univariate sensitivity analysis. In the sensitivity analysis, the NPV for the vinasse daily flow, the electricity sale price in the RCE, the contracted amount in the FCE, and the power limit of the installed plant were examined. The profitability of the process was also evaluated using a sensitivity analysis. Biogas reuse is governed primarily by investment costs for AD power plants and product prices (electricity or biomethane). In order to design an optimal control strategy for the bioprocess, Iancu and Petre [42] performed a system sensitivity analysis to determine how command and parameter changes affect the evolution of the system states and outputs.

Although the most commonly used sensitivity analysis method for adapted ADM1 models is the local sensitivity method, it has some drawbacks [26,73,74]. LSA does not consider interaction effects between parameters. Moreover, small variations and fluctuations make the analysis challenging [6].

Chen et al. [46] concocted a parametric sensitivity analysis on the ADM1 model using AQUASIM 2.0 (Reichert, 1994) to simulate biogas production from Hydrilla verticillata and select the most sensitive parameters for estimation using the absolute–relative sensitivity function. The results indicated that biogas production is greatly influenced by the disintegration constant (k_dis), the protein hydrolysis constant (k_{hyd_pr}), the maximum specific substrate uptake rate (k_{m_aa}, k_{m_ac}, k_{m_h2}), and the half-saturation constants (K_{s_aa}, K_{s_ac}). The model equations were optimized by fitting the batch experiment data to the model equations. They could predict the experimental results of daily biogas production and composition using their ADM1 model after parameter estimation. According to them, batch experiments alone are not sufficient to determine the actual biogas potential of HV under actual process conditions; continuous anaerobic digestion reactions will also be necessary. Furthermore, a future plan for their study was grouped into three steps: (1) developing an anaerobic digester with continuous flow, such as an up-flow anaerobic sludge blanket (UASB) or a continuously stirred tank reactor (CSTR); (2) analyzing the stability of the anaerobic reactor by applying the modified ADM1 model to simulations of continuous AD processes in CSTR or UASB reactors; and (3) experimentally verifying the predictive effects of the modified ADM1 model by conducting continuous AD experiments in the CSTR or UASB reactor.

In another study, Havlik et al. [65] applied a parametric sensitivity method to a mathematical model of anaerobic digestion in order to determine how individual model parameters affected selected output variables. According to the relative parametric sensitivity value, yield coefficients and rate constants were the most influential parameters in the process. As a result of the parametric sensitivity analysis of the anaerobic digestion model, it was concluded that the stoichiometric coefficients and rate constants should be evaluated with the highest priority during the construction of the model. In contrast, other coefficients, such as saturation and inhibition constants, had relatively little influence, and their order-of-magnitude estimates were sufficient for construction.

Barrera et al. [48] modeled the anaerobic digestion of cane-molasses vinasses. They extended ADM1 with sulfate reduction for high-strength and sulfate-content wastewater. Four parameters of the original ADM1 (k_m,pro, k_m,ac, k_m,h2, and Y_h2) and all sulfate reduction parameters (S_pro, S_ac, pH, Q_gas, S_gas,ch4, S_gas,co2, S_so4, S_h2s, and S_gas,h2s) were calibrated based on a local relative sensitivity analysis. It was found that the mentioned process variables were accurately predicted during model validation, despite some deviations between the model predictions and the experimental values. Thirty-six days of dynamic data were used to calibrate the model. Using an iterative approach [75], the most sensitive parameters were calibrated by fitting the model to the experimental results for the mentioned process variables. Their model showed high-to-medium accuracy (10–30%), with a mean absolute relative error ranging between 1 and 26%. As the sulfate loading rate increased, the model was able to predict the failure of methanogenesis and sulfidogenesis.

Lee et al. [50] conducted the anaerobic model for co-substrate degradation by a temperature-phased anaerobic digestion process based on ADM1 in order to validate the performance of ADM1. Moreover, dynamic sensitivity analyses of kinetic parameters were carried out. In order to analyze the dynamic sensitivity of the continuous experimental model, the average of absolute differences between simulation results with parameters previously determined by Batstone et al. [8] and parameters with a relative change of the target parameter was used as the sensitivity index. For sensitivity analysis, the kinetic parameters were taken into account. However, stoichiometric parameters were negligible due to their small variation. According to the sensitivity analysis, the maximum specific uptake rate and half saturation value were highly sensitive to model components. For propionate users and acetate utilizers, key parameters, including the maximum uptake rate and half saturation constant, were estimated using iterative methods, which optimized the parameters based on experimental results. For acetate utilizers, the maximum uptake rate was estimated using iterative methods.

Twelve of the thirty selected studies utilized GSA as the sensitivity analysis method. Based on a definitive screening design and multiple linear regression analysis, Boutoute et al. [1] demonstrated the reliability of a GSA methodology. The method was applied to a simplified model of anaerobic digestion. According to the sensitivity analysis, the slow hydrolysis constant and the upper pH inhibition limit of the hydrolytic biomass were crucial for accurate prediction of the biogas production rate, and biogas methane percentage varied slightly with kinetic parameters. Furthermore, the mass transfer coefficient significantly impacted the pH due to CO₂ desorption. Trucchia and Frunzo [6] conducted a GSA and uncertainty quantification (UQ) for a modified version of the ADM-based model. A large number of parameters were analyzed to perform GSA, which led to a first preliminary screening analysis using the Morris method. Based on the two defined quantities of interest (QoI), a surrogate model for ADM1 was developed. For the quantitative GSA, the output results from the surrogate model have been analyzed with Sobol indices. They resulted that for the whole set of QoI which was adopted, the role of parameters particle radius (r₀) and surface-based kinetic constant (K_sbk) were crucial.

A computational approach was demonstrated by Fortela et al. [45] in order to explore the importance of biochemical mechanism parameters in AD models with variations in the concentrations of feedstock. Their methodology incorporated GSA, functional principal component analysis (FPCA), and rank-clustering techniques. With GSA-FPCA integration, the time-varying nature of GSA (Morris’ indices) was removed, while rank-clustering provided a statistically based method to group parameter sensitivities based on variations in the feedstock. Based on the first principal component scores, the ranked Morris sensitivity indices revealed the stoichiometric parameters most likely to influence kinetic responses, as well as those that were the least sensitive. Pastor-Poquet et al. [60] evaluated the effect of high NH₃ levels on the high-solids anaerobic digestion of organic fractions of municipal solid waste through calibration and cross-validation of a high-solids anaerobic digestion model for homogenized reactors. Based on the experimental data available, the GSA was designed to identify the most influential parameter that should be calibrated. The identifiability of 35 biochemical parameters and 32 initial process conditions were assessed using batch experiments at different solid-to-substrate ratios.

Parameter optimization was carried out using variance-based global sensitivity analysis and approximate Bayesian computation. Xu [43] developed a method for calibrating parameters that could be incorporated into ADM1 built for industrial-scale digesters. A partial least squares (PLS) method was proposed, which consisted of four steps: a series of Monte Carlo simulations; GSA as a multivariate regression technique called PLS Regression, which was applied to the results in the previous step; parameter calibration; and validation. According to the author, the parameter calibration method proposed in this thesis significantly improved the model’s overall accuracy, and comparing the PLS method with other methods, such as Group and Brute Force methods, showed promising results. A systematic framework for the construction and validation of high-accuracy meta-models for the efficient scenario-based GSA of complex wastewater treatment plant models was presented by Al et al. [54]. Four engineering scenarios were investigated in order to assess the efficiency and robustness of three meta-modeling approaches, namely polynomial chaos expansion [76], Gaussian process regression [77], and artificial neural networks [78,79]. The proposed framework showed significant computational gains compared to the Monte Carlo-based approaches. An investigation into the influence of influent fractionation, kinetics, stoichiometry, and mass transfer parameter uncertainties on biogas production in wastewater treatment plants was conducted by Solon et al. [49]. Using BSM2, the amounts of CH₄, H₂, and CO₂ generated in a plant were quantified. In order to identify the set of parameters that have the greatest influence on the biogas production uncertainty, a comprehensive global sensitivity analysis was conducted based on standardized regression coefficients (SRC) and Morris’ screening’s (MS’s) elementary effects. GSA was repeated in the anaerobic digester for different solids retention times (SRTs) and temperature regimes. It resulted that unless the anaerobic digester operates at low SRT and mesophilic conditions, both SRC and MS are good sensitivity measures. The influent fractionation was the most influential parameter for predicting the emissions of CH₄ and CO₂ at high SRT.

Using one-dimensional secondary settling tanks (1-D SST) models with first-order and second-order mathematical structures, Ramin et al. [55] examined the sensitivity of wastewater treatment plant model performance. Based on the input uncertainties associated with the biokinetic parameters in ASM1, the fractionation parameter in the primary clarifier, and the settling parameters in the SST model, a GSA was performed on BSM2. In particular, for the biogas production and treated water quality in the plant model, the settling parameters were found to have the most influence on uncertainty as the biokinetic parameters. A study was conducted by Ramin et al. [39] to examine the impact of two operational strategies for reducing excess activated sludge waste on the simulation performance. They conducted GSA on BSM2 using linear regression (SRC method) with Monte Carlo simulations and Morris screening.