where α, β, and γ denote constants related to the unit cell size (L) in x, y and z, respectively; c is the offset parameter, which equals zero for a single unit cell of the TPMS.

The TPMS-based lattices can be constructed using two methods based on the minimal surfaces. The solid-based TPMS lattice, also known as the skeleton-based TPMS structure (Figure 2a), can be created with the first approach that is achieved by considering the volume bound by the minimal surface. The sheet-based TPMS lattice (Figure 2b) is the second one that is generated by offsetting the minimal surface along its normal direction. With mathematical realized, the TPMS-based structures have smooth curvature, which can eliminate the stress concentrations commonly found in other structures.

Figure 2 Examples of solid- and sheet-based TPMS lattices.

2. TPMS-Related Investigations

2.1. Mechanical Performances

The performances of the TPMS-based structure have been examined with other conventional structures. The majority of studies in various fields have investigated mechanical performances. Speirs et al. ^[8] reported that due to no nodal points in the TPMS structures, they outperformed the octahedron unit in terms of fatigue resistance. Khan et al. ^[9] demonstrated that in comparison to conventional lattice-frame materials, the sheet-IWP structures gave superior viscoelastic behavior under uniaxial loading. Wang et al. ^[10] presented that when compared to cubic and octet-strut-based designs, the sheet-Gyroid structure obtained the best stability and presented the widest variety of mechanical properties. Teng et al. ^[11] reported that in terms of stiffness, yield stress, and toughness, the sheet-Gyroid structure performed better than the BCC and truss lattices, as shown in Figure 3. Overall, TPMS-based lattices outperform strut-based structures in terms of mechanical performance. As a result, the TPMS-based structures, particularly those based on sheet-based ones, can be used in a variety of disciplines that demand high mechanical strength.

Figure 3 Normalized mechanical properties of the Gyroid, BCC, Truss and Primitive lattices with respect to the wall thickness, adapted from Teng et al. ^[11]

2.2. Mass Transfer

The TPMS structures are suitable for mass transfer applications because they have continuously curved walls and non-tortuous pores. Ali et al. ^[12] reported that the sheet-Gyroid structure provided comparable fluid permeability but higher wall shear stress than the lattice-based models. Montazerian et al. ^[13] showed that the solid-IWP structure was more permeable than different lattice-based models in the longitudinal fluid flow direction, as presented in Figure 4. Also, in a wide range of porosity, the TPMS-based scaffolds showed larger normalized permeability values than the fiber-based models ^[14]. Although the permeability increased with the porosity, the tortuosity of the fiber-based structure dramatically decreased ^[15], which had a detrimental effect on fluid mixing and heat transfer.

Figure 4 Normalized longitudinal permeability versus porosity for different lattices, adapted from Montazerian et al. ^[13]

2.3. Thermal Conductivity

The thermal conductivity of different TPMS-based structures has been tested by many designers. According to the experimental investigations by Wang et al. ^[16], compared to the commercial stochastic foams with the same porosity, the sheet-FRD structures achieved 103% higher thermal conductivity. It has been also observed by Ni et al. ^[17] that the normalized thermal conductivity values of the fiber-based porous media considerably varied with the fiber direction; hence, the sheet-based TPMS structures can also provide better thermal conductivity than the fiber-based models. The connection of the curved wall in the TPMS-based structure was the main factor in excellent thermal conductivity.

Also, it has been reported that the TPMS topologies have a significant impact on effective thermal conductivity. Qureshi et al. ^[18] presented that the sheet-Primitive structure exhibited the highest value, followed by IWP and Gyroid structures, while the Kevin model caused the lowest. Smith et al. ^[19] concluded that the thermal conductivity of the TPMS-based lattices was inversely proportional to the surface area-to-volume ratio. Overall, the thermal conductivity for most sheet-TPMS structures is significantly higher than stochastic metal foams and lattice-frame materials, as shown in Figure 5.

Figure 5 Normalized thermal conductivity for different lattices, adapted from Kaur and Singh ^[2]. Octet ^[20], Rhombi-Octet ^[21], Solid-Gyroid ^[22], Solid-Primitive ^[22], Sheet-CLP ^[22], Sheet-Neovius ^[22], Sheet-Fischer Koch S ^[22], Stochastic metal foam (Al) ^[23], Stochastic metal foam (FeCrAl) ^[24].

2.4. Forced Convective Heat Transfer

The TPMS-equipped heat sinks have a more complex geometry than typical pin-shaped heat sinks, causing the fluid to change trajectory as it passes the heated section ^[25][26]. The large surface area, smooth curved wall, and complicated topology of the TPMS-based structures are preferable for high-performance heat sinks. Moreover, the complexity level of the TPMS-based heat sinks can be controlled to enhance thermal performance since they are mathematically realized.

The globally averaged Nusselt number of the TPMS-based structures and different cooling geometries are plotted in Figure 6 to compare the heat transfer performance. It is evident that in comparison to the other cooling geometries, the TPMS-based structures exhibit higher globally averaged Nusselt numbers, particularly for the solid-Diamond structure. At the Reynolds number (Re) of 8000, the value for the solid-Diamond structure is much higher than the micro-lattice structure. The sheet-Gyroid structure causes the lowest values among the TPMS-based lattices. The solid-Diamond and solid-Gyroid lattices, on average, perform 1.27 and 1.23 times better than the sheet-Gyroid structure. However, it has been observed that the sheet-Gyroid structure shows higher values than the solid-Gyroid structure at Re > 6800 due to the strong fluid mixing.

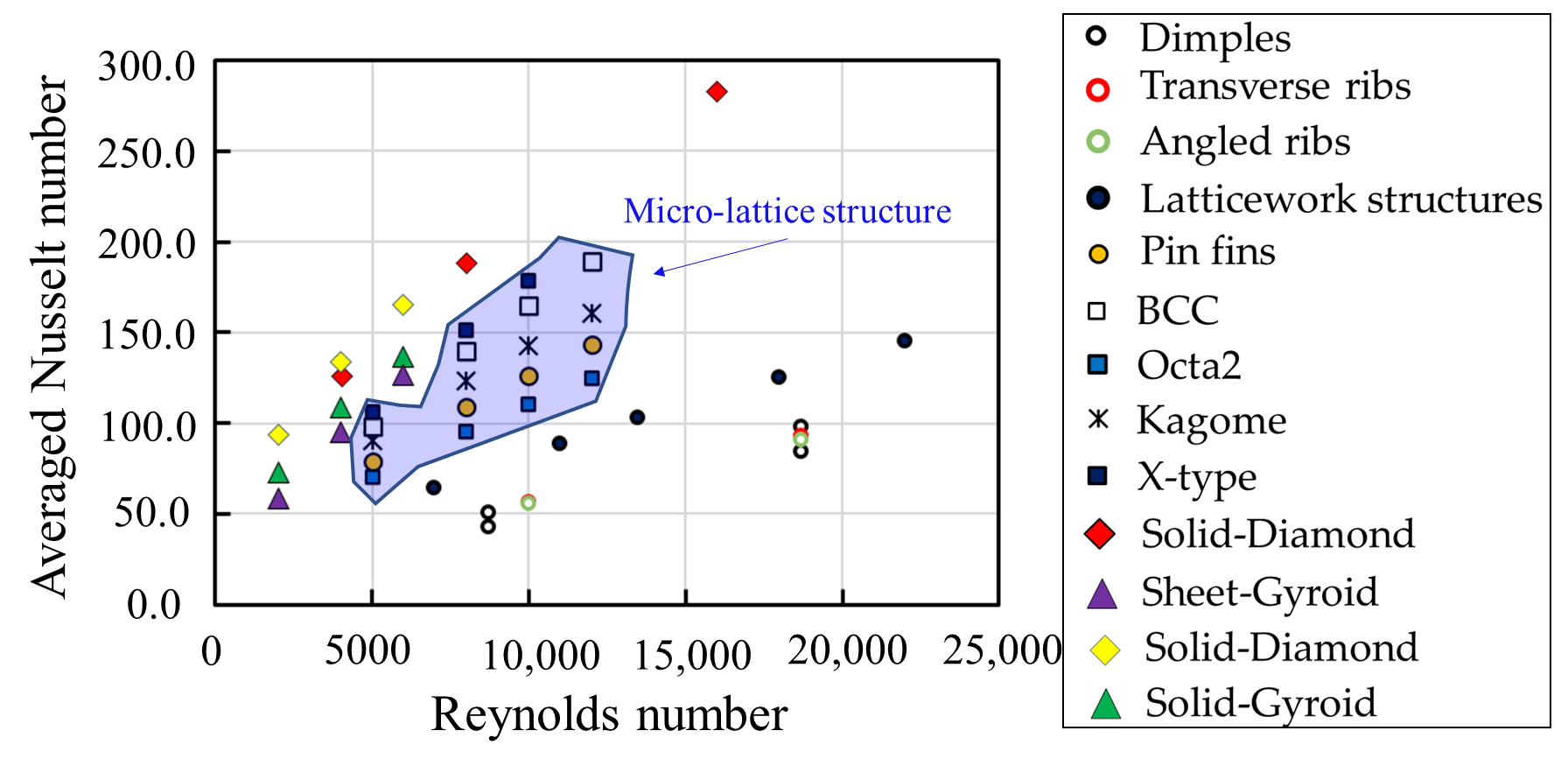
Figure 6 Comparisons of globally averaged Nusselt number. Dimples ^[27], Transverse ribs ^[28], Angled ribs ^[28], Latticework structures ^[29], Pin fins ^[21], BCC ^[21], Octa lattices ^[21], Kagome lattices ^[21], X-type lattices ^[21], Solid-Diamond structures ^[30][31], Sheet-Gyroid structures ^[31], Solid-Diamond structures ^[31], Solid-Gyroid structures ^[31].

The globally averaged Nusselt number ratio plotted against friction factor ratios for different geometries is shown in Figure 7 to compare the relative thermal performance. The results show with friction factor ratios between 55.0 and 75.0, the solid-Diamond structure achieves the highest Nusselt number ratio, up to 8.0-10.0. In comparison to the solid-Diamond structure, the solid Gyroid structure exhibits lower Nusselt number ratios with comparable friction factor ratios. Compared to micro-lattice structures, the sheet-Gyroid structure produces higher Nusselt number ratios and greater friction factor ratios. The ribs and dimples produce minor friction factor ratios between 1.2 and 3.0 while providing the lowest Nusselt number ratios, which range from 1.5 to 2.0.

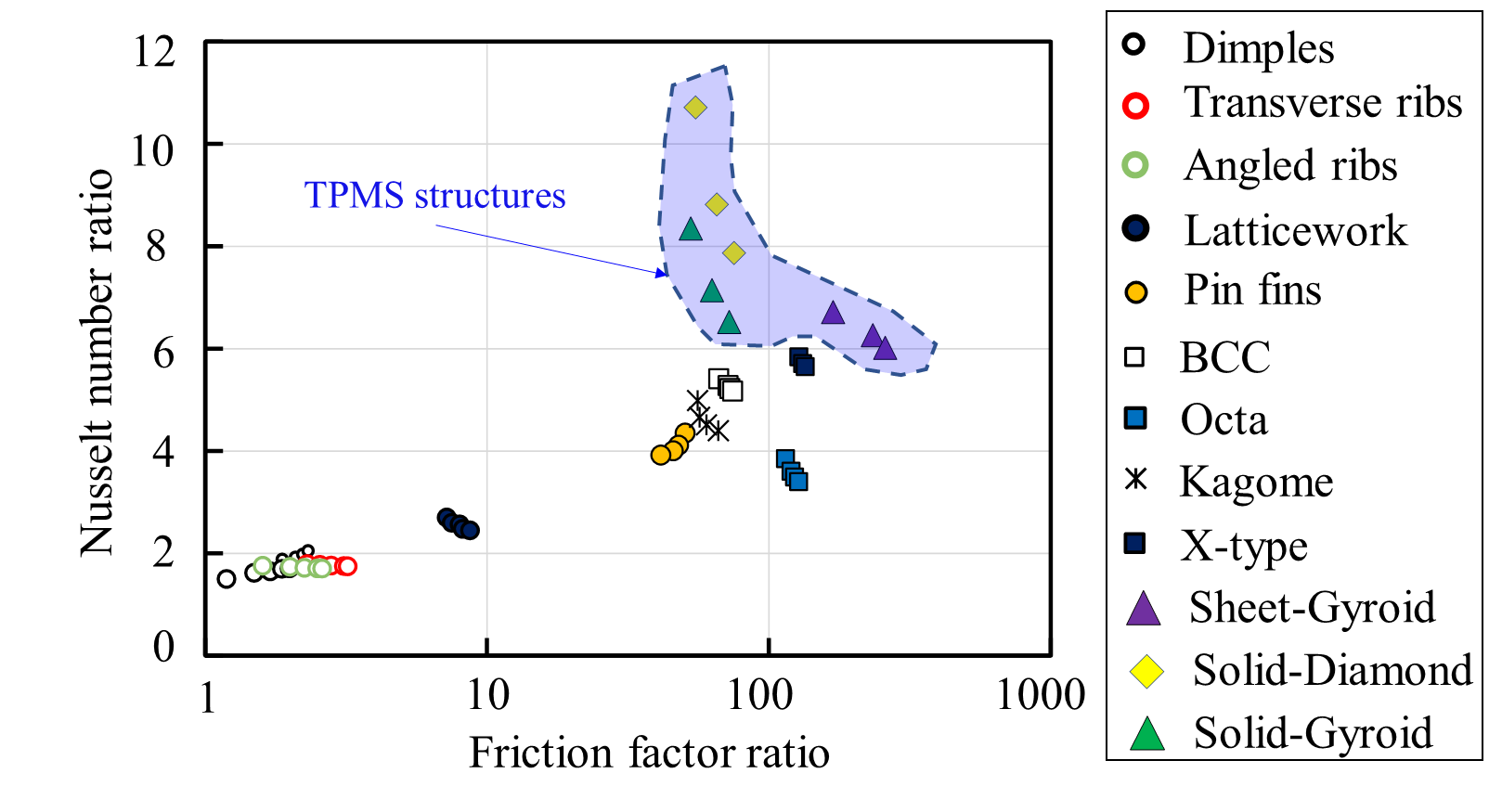
Figure 7 Relative thermal performance for different cooling structures. Dimples ^[27], Transverse ribs ^[28], Angled ribs ^[28], Latticework structures ^[29], Pin fins ^[21], BCC ^[21], Octa lattices ^[21], Kagome lattices ^[21], X-type lattices ^[21], Solid-Diamond structures ^[31], Sheet-Gyroid structures ^[31], Solid-Diamond structures ^[31], Solid-Gyroid structures ^[31].

2.5. Other Applications

In order to improve heat and mass transfer in membrane distillation, the TPMS-based structures are being investigated as spacers ^[32][33]. It was found that compared to commercial spacers, the TPMS-based spacers increased the overall film heat transfer coefficient by up to 60%.

The large surface area is essential for chemical reactions in catalytic supports and battery applications. Abu Al-Rub and Al-Ketan ^[34] proposed TPMS-based structures as catalytic substrates. Al-Ketan et al. ^[35] analyzed the flow characteristics of the solid- and sheet-TPMS-based substrates and revealed that the CLP topology showed a much lower pressure drop, while the Gyroid structure caused the highest pressure loss.

For organic PCMs (Phase Change Materials), various metallic TPMS-based architectures have been employed to improve thermal conductivity. It was found that in terms of heat transfer performance, the PCM embedded with the sheet-Primitive structure outperformed the PCM-alone cases ^[36], as presented in Figure 8. Also, Quereshi et al. ^[37] reported that the sheet-TPMS structures showed an increasing average heat transfer coefficient and minimized melting PCM time. Fan et al. ^[38] observed that the battery temperature was significantly improved by integrating the TPMS structure into a PCM-based battery thermal management system (BTMS). The average battery temperature was found to be around 40% lower with the addition of water as a working fluid for the PCM/TPMS-based BTMS, eliminating the thermal saturation of the PCM.

Figure 8 Comparisons of heat flux and liquid fraction for PCM only and Primitive PCM, adapted from ^[36].

Recently, Qureshi et al. ^[39] reported for the first time that TPMS models impregnated with PCM have been used for high heat flux cooling applications. It was observed that under conditions of high heat flux, the TPMS-based structures significantly reduced temperature. Moreover, they also found that because copper has good thermal conductivity, switching from aluminum powder (AlSi10Mg) to use as a heat sink resulting in better temperature control.

Baobaid et al. ^[40] compared the solid-Diamond, solid-Gyroid and sheet-Gyroid structures for three boundary conditions in the free convection. It was found that when opening the top and bottom surfaces of the enclosure, the sheet-Gyroid structure provided better thermal performance. Still, its surface temperature was the highest when opening the sides and top surfaces. They summarized that the flow resistance within the complex structure of the sheet-Gyroid construction was very high, which significantly reduced thermal performance.

3. Effects of TPMS Design Variables on Flow and Heat Transfer

3.1. Porosity

The porosity (ε) is defined as the fluid volume divided by the total volume of the channel. It has been mostly maintained at equivalent values to compare the effects of TPMS topologies. The porosity values can be set to the same values in the uniform or graded TPMS-based structures. Moreover, to investigate the flow and heat transfer characteristics, the porosity of the specific TPMS topology has been changed in various research.

3.1.1. Equivalent porosity

The majority of studies have examined the flow, heat, and mass transfer for various TPMS-based structures with uniform porosity in laminar flow systems. For heat exchanger applications, Cheng et al. ^[41][42] noted that with increasing Reynolds numbers, the interstitial Nusselt number values for the sheet-Primitive structure marginally increased. The values for the sheet-Diamond, sheet-IWP, and sheet-Gyroid structures, on the other hand, increased in a quasilinear fashion because the complex curvatures broke the boundary layer.

The averaged heat transfer coefficients of the sheet-Gyroid and sheet-Primitive structures with an equivalent porosity for heat sink applications were compared by Kaur and Singh  ^[43]. The simulation results showed that compared to the sheet-Primitive structure, the sheet-Gyroid structure had a higher heat transfer. Even though the sheet-Gyroid structure resulted in a high-pressure loss in the channel, it performed better than the sheet-Primitive structure under particular pumping power conditions. Sreedhar et al. ^[33] reported that compared to other TPMS architectures, the solid-Gyroid structure significantly increased mass transfer and decreased pressure loss. Similar results were also acquired by Thomas et al. ^[44], which further found that although the tCLP topology had a higher pressure loss than the other TPMS structures, it showed a better overall film heat transfer coefficient.

For turbulent flow systems, the flow characteristics and heat transfer capabilities of a cooling channel at a particular porosity have also been investigated. Yinzheng et al. ^[45] showed that due to the greater heat dissipation area in the solid-Diamond structure, it had the best heat transfer performance. The solid-Primitive lattice, meanwhile, caused the lowest channel flow resistance. Al-Ketan et al. ^[30] found that the sheet-Gyroid structure has the highest convective heat transfer coefficient due to its complex curved wall. Among these TPMS topologies, Khalil et al. ^[31] observed that as the Reynolds number increased, the solid-Diamond structure had the best thermal performance as a result of reasonably increased pressure loss and significantly improved heat transfer. Additionally, the sheet-Gyroid structure presented the lowest thermal performance in the comparison since it caused the highest-pressure loss.

According to Al-Ketan et al. ^[30], the variation in pressure loss in the channel was due to the different pore sizes, as seen in Figure 9. The diameter of the maximum sphere (red sphere) that fits the smallest hole of the TPMS-based structure is employed to describe the pore size. It can be observed that the sheet-Gyroid structure has the smallest pore size, followed by the solid-Diamond and solid-Gyroid structures. Hence, the sheet-Gyroid structure causes the highest pressure loss.

Figure 9 The maximum sphere, fitting the smallest hole of different TPMS lattices: (a) Sheet-Gyroid structure; (b) Solid-Diamond structure; (c) Solid-Gyroid structure, adapted from ^[30].

For improving the cooling performance, the grading of the porosity of TPMS-based structures has been investigated in a number of research. The graded TPMS structure has the same overall porosity as a uniform TPMS structure but gradually changes the TPMS porosity along the length, width, or height of the channel.

Qureshi et al. ^[46] showed that in terms of conductive and convective heat transfer capabilities, the gradually increased porosity along the flow direction outperformed the uniform and gradually decreased porosity models for different sheet-TPMS structures. Moreover, Al-Ketan et al. ^[30] reported that under turbulent flow regimes, the solid Diamond structure with porosity varied from 80.0-82.5% along the flow direction reduced the pressure loss by roughly 27.6% while only reducing the overall heat transfer coefficient by 15.7%.

Figure 10 shows the velocity vector for uniform and graded diamond-solid structures, investigated by Al-Ketan et al. ^[30]. As seen the Figure 10a, for the uniform structure, the velocity increases gradually due to the fluid expansion. In the case with negative grading porosity in Figure 10b, the velocity entering the high porosity structure is lower than the corresponding uniform one. This reduction is attributed to the small structure that lesser disturbs the incoming fluid. However, a higher velocity can be observed as the structure is larger downstream. The velocity distribution in this channel is non-uniform as compared to the others. For the case with a positive grading structure in Figure 10c, the velocity increases significantly when the fluid enters the low porosity structure. The velocity magnitude remains similar throughout the channel, indicating better uniformity distribution of the flow.

Figure 10 Velocity vectors of the uniform and graded diamond-solid structures at Re = 65,326, studied by Al-Ketan et al. ^[30].

Although the graded TPMS structures showed reasonable heat transfer reductions, they offer higher cooling channel thermal performance. Also, the graded TPMS-based structures resulted in lighter cooling channels by using less material during additive manufacture. However, due to other crucial factors like mechanical strength, hydraulic performance, etc., the graded TPMS-based structures might not be superior to the uniform ones for some functions ^[47].

3.1.2. Varying the porosity

The overall contact area is significantly impacted by the porosity variation for a TPMS-based structure, which influences the flow, heat, and mass transfer. The solid-Gyroid model with greater porosity, according to Sreedhar et al. ^[33], was observed to significantly enhance mass transfer and reduce pressure loss. However, different investigations found that the porosity of the sheet-TPMS structures had an inverse relationship with the convective heat transfer coefficient and friction factor ^[48][49].

Qureshi et al. ^[46] found that the convective and conductive heat transfer were significantly improved in a lower porosity for the sheet-Primitive, sheet-Gyroid, and sheet-IWP structures. Similarly, Cheng et al. ^[41] reported that the interstitial convective heat transfer coefficient reduced as the porosity increased for the sheet-IWP, sheet-Diamond, and sheet-Gyroid structures because the velocity declined at the higher porosity. However, due to the larger heat transfer area at the higher porosity values in the sheet-Primitive structure, the convective heat transfer coefficient increased, as illustrated in Figure 11.

Figure 11 Effect of porosity on convective heat transfer coefficient for different TPMS structures at Re = 40, adapted from ^[41].

3.2. Wall Thickness

The relative wall thickness (t) of various TPMS topologies has been defined in order to explore the effect on the flow and heat transfer performance. It should be noted that due to topology differences, the values of porosity (ε), pore size (d_pore), and surface area at c = 0 (A_TPMS) are changed for each TPMS topology at a homogenous wall thickness and unit cell size ^[50], as shown in Figure 12. It can be observed that the sheet-Diamond structure has the largest surface area and the same pore size as the sheet-Gyroid structure, whereas the sheet-Primitive structure has the lowest surface area and the largest pore size.

Figure 12 Variations in porosity, pore size, and the surface of TPMS at c = 0 at the wall thickness of t = 0.1 mm and unit cell size of L = 2.0 mm for a unit cell of sheet-based TPMS structures (The correlations for the porosity, pore size and surface area are provided by Poltue et al. ^[50]): (a) Sheet-Gyroid; (b) Sheet-Primitive; (c) Sheet-Diamond; (d) Sheet-IWP structures.

In the laminar flow system, according to Femmer et al. ^[51], the heat exchanger with the sheet-Diamond structure outperformed the sheet-Gyroid, sheet-IWP, and sheet-Primitive structures in terms of heat transfer performance for inherent pressure loss. Similar findings were reported by Passos ^[48], who found that the sheet-Diamond structure had the best thermal performance. Genç et al. ^[49] noted that the sheet-Diamond structure produced the highest pressure loss compared to the sheet-Gyroid and sheet-Primitive structures. Additionally, for all TPMS designs, the friction factor reduced as the Reynolds number increased.

Iyer et al. ^[52] reported that the lowest values of the Nusselt numbers were found in the sheet-Primitive structure, as shown in Figure 13a. Meanwhile, the sheet-Diamond structure exhibited the best heat transfer performance, followed by the C(I₂-Y**). As shown in Figure 13b, the other TPMS structures provided a comparable pressure loss within the Reynolds numbers range between 0-300, whereas the sheet-Neovius structure caused the highest values, followed by the sheet-FRD structure. It was also reported that the pressure losses are lower than Femmer et al.  ^[51] and Kaur and Singh ^[43] because the semi-infinite curved wall of the TPMS structures has been set.

Figure 13 Comparisons of the Nusselt number and friction factor of different TPMS topologies for the same infinitesimally thin walls (The correlations are provided by Iyer et al. ^[52]): (a) Averaged Nusselt numbers; (b) Friction factors.

According to Li et al. ^[53], the thermal performance of the sheet-Gyroid structure was superior to the sheet-Diamond model at high Reynolds numbers. The substantial increase in turbulent kinetic energy (TKE) due to the fluid mixing at high Reynolds numbers in the sheet-Gyroid structure is the reason that makes high heat transfer, which shows the different results from the earlier investigations ^[48][51].

Attarzadeh et al. ^[54] investigated the effects of varying thicknesses of the sheet-Diamond structure on the flow and heat transfer performance for a heat sink cooling channel under laminar flow. They claimed that while the larger wall thickness increased the convective heat transfer coefficient, it impeded the flow field, lowering the thermal performance of cooling channels. Figure 14 illustrates the continual decline of reverse flow in the channel, which lowers pressure loss as the wall thickness is decreased. Due to low-pressure loss and a moderate increase in heat transfer, the lowest thickness demonstrates the best thermal performance in their simulations.

Figure 14 Demonstrations of reverse flow regions for small thickness (left) and large thickness (right) of the sheet-Diamond structure at a specific Reynolds number ^[54].

Later, to find the optimal configurations, Attarzadeh et al. ^[55] investigated a multi-objective optimization approach based on a Genetic Algorithm for laminar flow. The sheet-Gyroid structure was chosen to investigate the TPMS design variables. It was shown that better thermal performance resulted from thicker walls. Additionally, they claimed that the pore size and wall thickness exhibited the greatest Pareto sensitivity during the optimization. It should be noted that since the TPMS topologies and unit cell sizes used in the study are different, the results did not disagree with the earlier findings by Attarzadeh et al. ^[54].

3.3. Unit Cell Size

The unit cell size for the TPMS topologies affecting the flow and heat transfer performances are rarely discussed in the literature. According to Zimmer et al. ^[56], the largest unit cell sizes caused the low-pressure loss in the system, whereas the smallest one significantly increased pressure loss, especially at higher velocities. Similar to this, Al-Ketan et al. ^[35] discovered that the sheet-Gyroid and sheet-Primitive structures with the smaller unit cell size caused higher pressure loss because of more complicated geometries and lower porosities. As shown in Figure 15, it can be inferred that a smaller unit cell size resulted in higher pressure loss because of the lower porosity but increased heat transfer due to the larger specific surface areas (Sv). Later, according to Attarzadeh et al. ^[55], reducing the unit cell size enhanced the thermal performance of the heat exchanger. 

Figure 15 The sheet-Gyroid structures with different unit cell sizes at the same thickness of 0.6 mm, adapted from ^[35].

4. Conclusion

Recent experimental and numerical investigations have been extensively analyzed to highlight the effects on flow and heat transfer enhancement in cooling channels with Triply Periodic Minimal Surfaces (TPMS). The effects of wall thickness, porosity and unit cell size on the flow field and heat transfer from the extensive results. are demonstrated and discussed. The following are the main conclusions:

1. With the same porosity, as the Reynolds numbers increase, more complicated TPMS topologies, such as the Diamond and Gyroid models, achieve high heat transfer but result in substantial pressure loss. Their tortuous topologies and greater surface areas, which significantly alter the flow characteristics, are the main reason for this increase. The graded TPMS-based structure that increases the porosity along the flow direction presents higher thermal performance than the uniform one due to lower pressure loss while maintaining high heat transfer in the channel.
2. The porosity in the majority of the sheet-TPMS structures has an inverse relationship to the convective heat transfer coefficient and the friction factor. Except for the sheet-Primitive structure, a high-speed velocity area along the flow direction interacts with the heating walls in the lower porosity model.
3. With the same wall thickness, different TPMS structures show a difference in the porosity and surface area, which changes flow and heat transfer characteristics in the channel. Under laminar flow, the Diamond structure provides the best thermal performance. In contrast, for turbulent flow systems, the Gyroid obtains better heat transfer because of increased turbulent kinetic energy. However, due to the TPMS topologies and unit cell sizes, the wall thickness variation affects the flow field and heat transfer enhancement differently. However, most of the research found that the larger wall thickness exhibits larger convective heat transfer and pressure loss.