Structure and Bonding in Planar Hypercoordinate Carbon Compounds: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Prasenjit Das
,
Pratim Kumar Chattaraj

The term hypercoordination refers to the extent of the coordination of an element by its normal value. In the hypercoordination sphere, the element can achieve planar and/or non-planar molecular shape. Hence, planar hypercoordinate carbon species violate two structural rules: (i) The highest coordination number of carbon is four and (ii) the tetrahedral orientation by the connected elements and/or groups. The unusual planar orientations are mostly stabilized by the electronic interactions of the central atom with the surrounding ligands. Primary knowledge of the planar hypercoordinate chemistry will lead to its forthcoming expansion. Experimental and theoretical interests in planar tetracoordinate carbon (ptC), planar pentacoordinate carbon (ppC), and planar hexacoordinate carbon (phC) are continued. The proposed electronic and mechanical strategies are helpful for the designing of the ptC compounds. Moreover, the 18-valence electron rule can guide the design of new ptC clusters computationally as well as experimentally. However, the counting of 18-valence electrons is not a requisite condition to contain a ptC in a cluster. Furthermore, this ptC idea is expanded to the probability of a greater coordination number of carbon in planar orientations. Unfortunately, until now, there are no such logical approaches to designing ppC, phC, or higher-coordinate carbon molecules/ions. There exist a few global minimum structures of phC clusters identified computationally, but none have been detected experimentally. All planar hypercoordinate carbon species in the global minima may be feasible in the gas phase.

  • anti-van’t Hoff Le Bel
  • planar tetracoordinate carbon
  • planar pentacoordinate carbon
  • planar hexacoordinate carbon

1. Planar Tetracoordinate Carbons (ptCs)

1.1. How to Achieve ptCs

Methane (CH4) is the simplest hypothetical ptC molecule to think about. The hybridization changes from sp3 to sp2 for the planar D4h configuration. The planar configuration is approximately 130 kcal mol−1 higher in energy compared to the lowest-energy tetrahedral geometry [1]. Even the planar structure has higher energy than the C–H bond detachment energy (103 kcal mol−1) [2]. After the analysis of the electronic structure of the planar CH4 molecule, Hoffmann and co-workers suggested a way to stabilize the planar structures. When the tetrahedral structure of methane becomes planar, an extra lone pair is available on the central carbon, which distorts its planar geometry. The other point is the electron-deficient nature of the C–H bonds in the planar form. They suggested that the replacement of hydrogens by σ-donor ligands overcome the electron deficiency problem of the C–H bonds, as the ligands give electrons to the carbon atom. The ligands should have π-acceptor capacity so that they can accept the lone pair on the carbon. So, with the incorporation of simultaneous σ-donor and π-acceptor ligands, a ptC structure can be generated, and this strategy is called the “electronic approach”. Using this approach, many ptC molecules have been theoretically reported [3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21],[22],[23],[24]] and experimentally characterized [25][26][27][28][29][30][31][32][33].
In addition to the electronic approach, ptC structures can be designed by generating enough strain to keep the carbon forcefully in planar orientations, and this method is called the “mechanical strategy”. In this particular approach, to generate sufficient strain, cylindrical cages or tubes, small rings, and annulenes are helpful agents [34][35][36][37][38][39][40]. Although some species with ptC were designed theoretically by using this strategy, no experimentally characterized ptC structures based on this strategy have been reported. Following this strategy, some of the computationally predicted ptC species are shown in Figure 1. To achieve ptC structures based on this approach, the fenestrenes and the aromatic unsaturated fenestrenes, rigid 3D cages, such as octaplane, were proposed initially [41][42]. In 1999, Ding et al. noted that “despite considerable computational efforts no structures with a planar tetracoordinate C(C)4 substructure have been found” [43]. However, Rasmussen et al. computationally reported the first successful ptC structure based on this strategy by adjusting the 1g structure to generate 1h (Figure 1) geometry in which the ptC atom is stabilized in a strained environment [37][44]. With the use of a similar strategy, Wang and Schleyer reported a set of boron spiroalkanes with a planar C(C)4 moiety through the replacement of carbon by boron atoms [9][45].
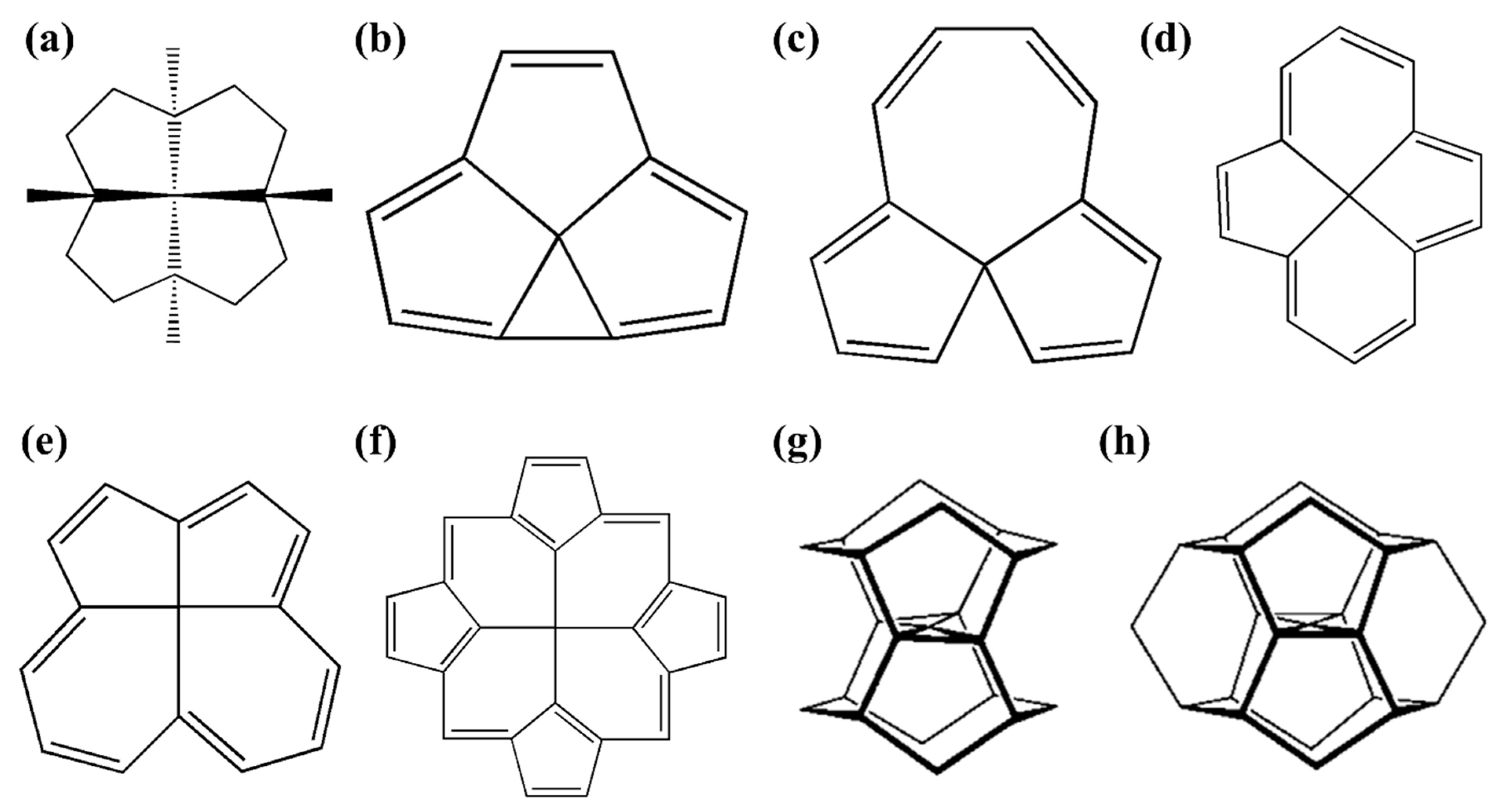
Chemistry 04 00113 g001 550
Figure 1. Schematic presentations of various mechanically stabilized ptC molecules (a–h).

1.2. Early Examples of ptCs

With the help of the two suggested strategies, the first example of ptC came from Collins et al. in 1976 [46]. Through a systematic computational investigation, they reported 1,1-dilithiocyclopropane (Figure 2a) and 3,3-dilithiocyclopropene (Figure 2b) systems with ptCs in the energy minimum geometries and the tetrahedral orientations have higher energies than the corresponding planar configurations. One year later, the first experimentally characterized ptC containing compound V2(2,6-dimethoxyphenyl)4 (Figure 2c) was published by Cotton et al. [47]. This complex contains triple bonds between two vanadium (V) centers and has two ptCs at two ligand rings. However, unfortunately, at that time, the original authors did not realize this beautiful fact. This system has importance in this background as it is the first experimentally predicted ptC-containing compound. Due to the ionic bonding nature of lithium (Li), it prefers bridging positions, and with this concept, Xie et al. in 1991 designed a D6h symmetric C6Li6 system with ptCs (Figure 2d) [48]. The simplest molecule with a ptC has only five atoms, and the first example of this category was CAl2Si2, which was reported in 1991 by Schleyer and Boldyrev [4]. They concluded that cis and trans isomers of CSi2Al2 (Figure 3a and 3b, respectively) were local minimum geometries with a ptC, but they did not mention the energy of the tetrahedral-like geometry of this system. They first introduced the 18-valence electron counting concept for the stabilization of planar geometries. After seven years, in 1998, Boldyrev and Simons computed the energies of the planar and tetrahedral-like geometries of the CSi2Al2 system, and then they expanded the search for the possibility of a ptC atom in higher analogues such as CSi2Ga2 and CGe2Al2 species in order to determine the size dependency of the surrounding atoms on the stabilities of these species in planar orientations [5]. The optimized structures of CSi2Al2 in singlet states are given in Figure 3. The cis and trans isomers of the CSi2Al2 system are energy minima based on the theoretical analysis using the B3LYP/6-311+G* method, which is in agreement with the earlier conclusion at the MP2/6-31G* level of theory. However, both these isomers become saddle points in the MP2(full)/6-31+G* and MP2(full)/6-311+G* methods [5]. The authors reported that in the case of the CSi2Al2 system, the tetrahedral-type geometry is a first-order saddle point in the B3LYP/6-311+G* and MP2(full)/6-311+G* methods and has almost 27−28 kcal mol−1 higher energy than the more stable quasi planar cis and trans isomers 3a and 3b, respectively (Figure 3) [5]. Then they studied two 18-valence isoelectronic species, CSi2Ga2 and CGe2Al2, where the cavities for the carbon center happened to be larger than that in the CSi2Al2 system. However, this time they only optimized planar cis and trans and tetrahedral geometries for CSi2Ga2 and CGe2Al2 systems. In the B3LYP/6-311+G* and MP2(fc)/6-311+G* methods, the planar cis and trans isomers of both these species were reported as energy minima [5]. However, the cis isomer (Figure 3c) of CSi2Ga2 is less stable than the trans isomer (Figure 3d) by 2 kcal mol−1, while, for the CGe2Al2 system, the cis isomer (Figure 3e) has 3 kcal mol−1 lower energy than the trans isomer (Figure 3f). They also reported that the tetrahedral-type geometries have 27 and 25 kcal mol−1 more energy than the most stable isomers for CSi2Ga2 and CGe2Al2 systems, respectively. The increase in the size of the cavity in the CSi2Ga2 and CGe2Al2 species permits the incorporation of carbon into it and thus maintains the planar structures. From these analyses, they concluded that pentatomic species with a carbon center and two Al or Ga and two Si or Ge surrounding atoms should have stable planar geometries [5]. The planar structures may be preferred over the tetrahedral one when Jahn−Teller distortion makes the tetrahedral geometries unstable and the formation of the maximal carbon–ligand and ligand−ligand bonding by the valence electrons. For this purpose, they compared the occupancy pattern of the valence molecular orbitals (MOs) of the tetrahedral CF4 molecule with the tetrahedral structures of their systems. The CF4 molecule is a 32-valence electronic system, and the occupancy pattern of the occupied MOs is 1a121t262a122t261e43t261t16. They assumed other tetrahedral molecules or nearly tetrahedral structures will follow this occupancy pattern (except for symmetry-imposed degeneracies) and the 18-valence electronic tetrahedral structures show 1a121t262a122t261e2 pattern of occupancy. Due to this partially filled e-orbital, the tetrahedral structures of their systems show Jahn–Teller instability and become distorted to a planar structure. They suggested that the presence of 18-valence electrons is crucial for planar geometries to be stable and preferred over tetrahedral structures. The formation of three σ and one π bonds among the middle carbon and the surrounding atoms and one ligand–ligand bond are the consequences of 18-valence electrons, the appeasement case for planar geometries. It took a long time to encourage experimental researchers to test this prognosis. Nevertheless, the species CAl4− and CAl3Si− (isoelectronic to CSi2Ga2) were prepared in molecular beams and the planarity of these systems was experimentally confirmed [7][33][49].
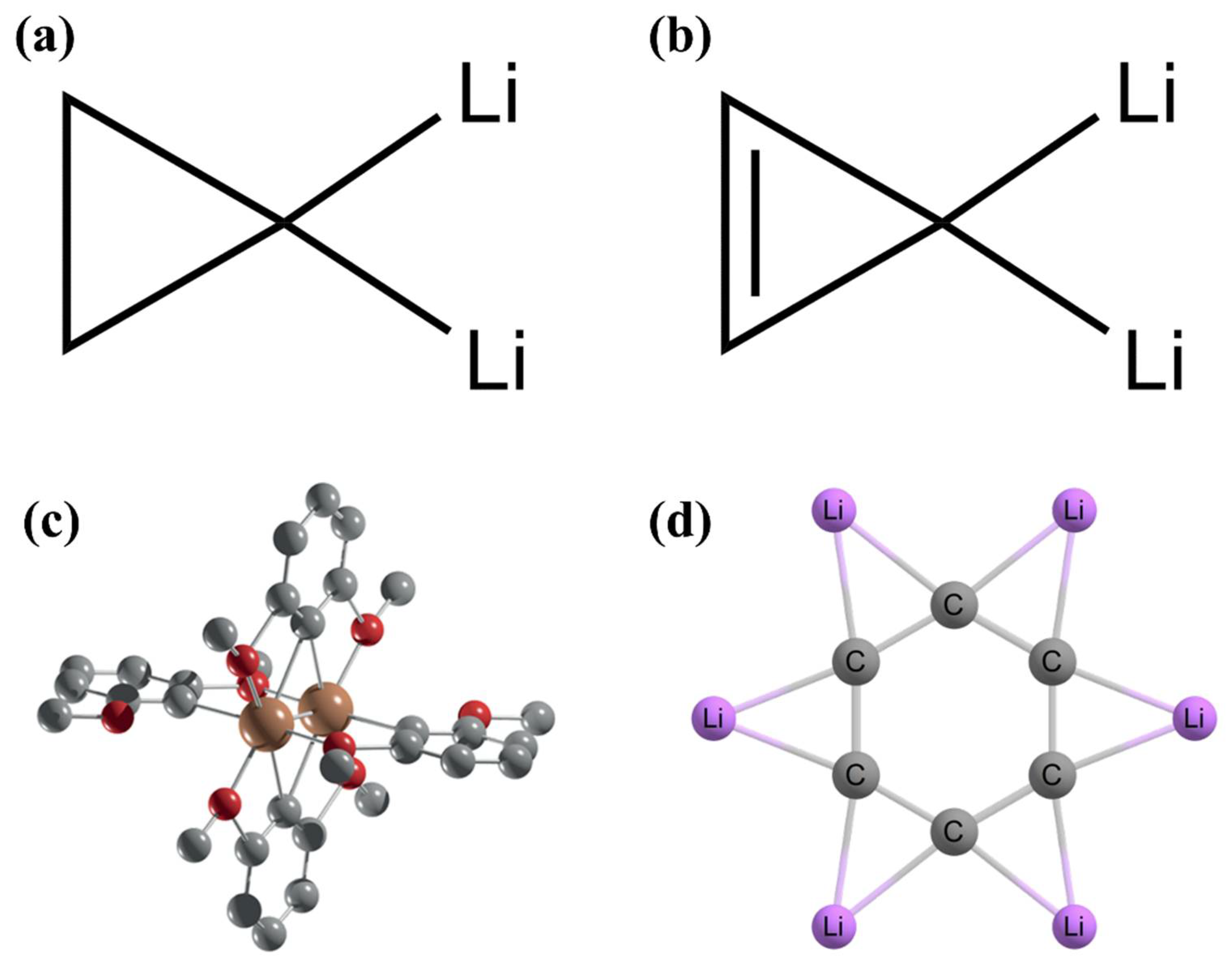
Chemistry 04 00113 g002 550
Figure 2. Optimized geometries of (a) 1,1-dilithiocyclopropane and (b) 3,3-dilithiocyclopropene systems. (c) The molecular structure of V2(2,6-dimethoxyphenyl)4 features a V≡V triple bond and two planar tetracoordinate carbon (ptC) centers. The H atoms are omitted for clarity. (d) Optimized D6h symmetric structure of C6Li6.
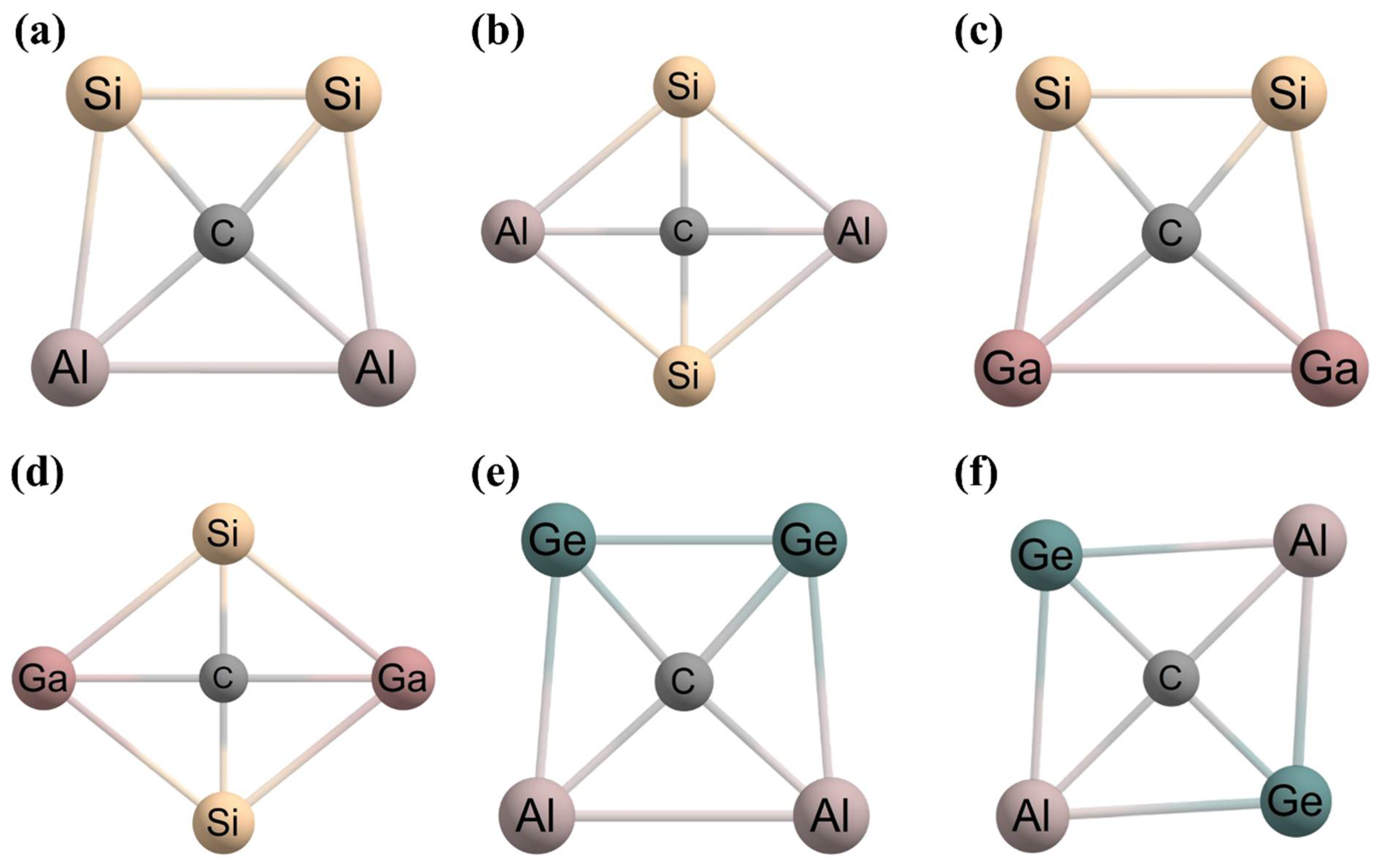
Chemistry 04 00113 g003 550
Figure 3. Optimized geometries of (a) cis-CSi2Al2, (b) trans-CSi2Al2, (c) cis-CSi2Ga2, (d) trans-CSi2Ga2, (e) cis-CGe2Al2, and (f) trans-CGe2Al2 systems. Structure (a) has 1.16 kcal mol−1 lower energy than structure (b). Structure (c) has 2.01 kcal mol−1 higher energy than structure (d). Structure (e) has 2.87 kcal mol−1 lower energy than structure (f).
With the use of Li as ligand atoms, a series of ptC species can be adapted [8]. For example, the replacement of the CH2 group in the 1,1-dilithiocyclopropane (Figure 2a) molecule by isoelectronic NH and O generates ptC structures 4a and 4b, respectively (Figure 4). The 4c and 4d ptC structures are also generated by attaching 4a to a heterocyclic system and a benzene ring, respectively. These 4c and 4d species are more viable targets due to the dominance of the aromaticity of imidazole.
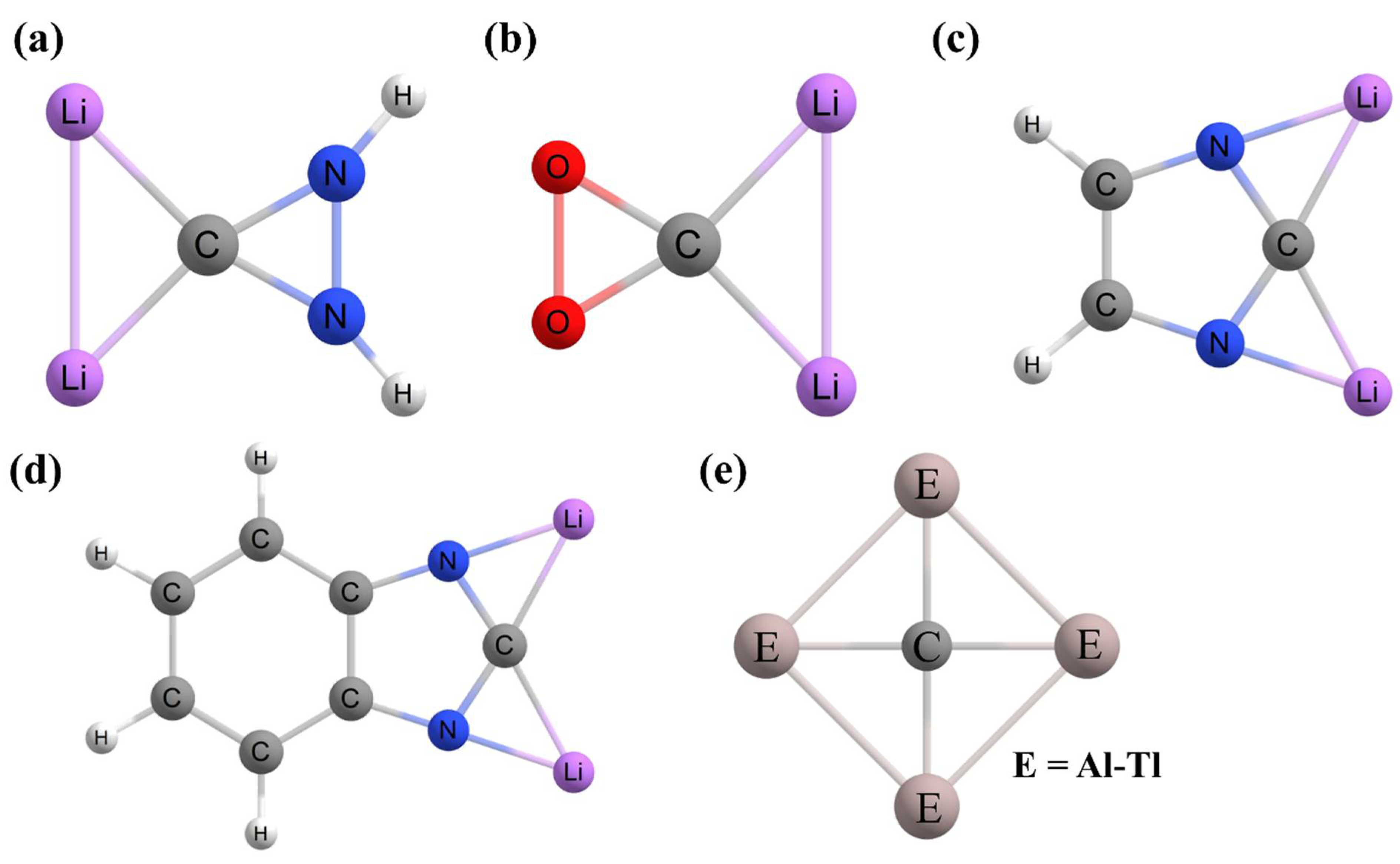
Chemistry 04 00113 g004 550
Figure 4. Optimized geometries of (a–d) computationally predicted dilithium ptC compounds.

2. Planar Pentacoordinate Carbons (ppCs)

The idea of ptC is expanded to the probability and representation of systems with ppC centers [50]. In 1995, Bolton et al. reported the singlet 1,1-dilithioethene molecule (Figure 5a) with the help of the ab initio quantum mechanical methods, which show the ppC local minimum structure having 7.2 kcal mol−1 more energy compared to the lowest-energy isomer with a ptC atom [51]. The barrier height for the interconversion between the ppC and the lowest-energy ptC isomers is approximately 0.4 kcal mol−1 indicating that it is impossible to characterize the ppC isomer experimentally.
Chemistry 04 00113 g018 550
Figure 5. (a) A C2v-symmetric ppC-containing isomer of 1,1-dilithioethene contains two bridging Li centers. The computed structures of (b) Cu5H5C, (c) Ag5H5C, and (d) Au5H5C each feature bridging hydrides and a ppC. The global minimum energy structures of (e) CAl5+, (f) CAl4Be, and (g) CAl3Be2− clusters.
After the detection of the aromatic M5(μ-H)5 hydrometal rings (M = Cu, Ag, Au) [52][53], Li et al. placed one carbon atom at the center of the Cu5(μ-H)5 ring and found a perfect D5h symmetric true local minimum structure with a ppC (Figure 5b) [54]. Although the Cu5(μ-H)5 ring is aromatic in nature, the inclusion of the carbon causes the nonaromaticity of the ring. Further, the Ag5H5C (Figure 5c) and Au5H5C (Figure 5d) molecules also have a ppC in their local minimum geometries [55].
The first global minimum geometry with a ppC in the CAl5+ system with D5h symmetry (Figure 5e) was reported based on an extensive potential energy surface (PES) search in 2008 by Zeng and co-workers [56]. This ppC geometry is 3.8 kcal mol−1 lower in energy than the second-lowest C2v isomer of this system. This system is also consistent with the electronic stabilization strategy approach given by Hoffmann and coworkers, and the presence of the back donation from the central carbon to the peripheral atoms is also reported by them. Moreover, the aromaticity analysis based on the nucleus-independent chemical shift (NICS) computations [[57],[58],[59],[60]] of this ppC system has been carried out by these groups.
After one year, Wang and coworkers substituted the Al atoms with isoelectronic Be atoms to generate neutral CAl4Be (Figure 5f) and mono-anionic CAl3Be2− (Figure 5g) systems containing ppCs in the global minimum structures [61]. The aluminum–carbon bond distances are between 2.08 and 2.29 Å, which are somewhat lengthy compared to the value of the normal aluminum–carbon bond distance of 2.00 Å but close to the 2.12 Å values as predicted theoretically for the CAl5+ system. The bonds among the central carbon and the surrounding Be and Al atoms are longer by 0.08 Å to 0.29 Å than the corresponding normal values. The molecular dynamics simulation suggested the dynamic stability of these global minimum ppC isomers. The highly negative charges on the carbon are the consequences of the σ-donation from the surrounding atoms. At the same time, the carbon lone pair is donated to the ligand atoms. Therefore, the central carbon in the global minimum structures acts as the σ-acceptor and π-donor. The energy differences between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are 2.6 eV for both ppC structures indicating the greater stability of these isomers [61].
Wu et al., in 2012, reported di-anionic CAl2Be32− (Figure 6a) and its mono-anionic salt complex LiCAl2Be3− (Figure 6b) systems by further replacement of Al atoms by Be atoms [62]. The PES search shows the global minimum geometry of these clusters has a ppC. The vertical detachment energy (VDE) for the CAl2Be32− cluster is negative (−1.10 eV) indicating that this species is unstable toward electron release. However, the instability of this cluster is resolved by adding one Li+ to neutralize one negative charge, and the most preferable binding site of Li+ is the Be–Be bond in the LiCAl2Be3− cluster. In the LiCAl2Be3− system, the first computed VDE is 2.28 eV, indicating that the automatic removal of the additional electron is partially eliminated. Moreover, the energy gap between the HOMO and LUMO increases from 0.94 eV in CAl2Be32− to 1.79 eV in the LiCAl2Be3− system. Hence, from these stability comparisons, it is clear that LiCAl2Be3− system is more achievable than the CAl2Be32−cluster [62]. The dynamical stability of the global minimum structures was confirmed at 4 K and 298 K temperatures up to 100 ps simulation time. The natural charge analyses indicate that the addition of Li+ to the CAl2Be32− system influences the ionic bonding, but the covalent bonds are not markedly affected.
Chemistry 04 00113 g020 550
Figure 6. The global minimum energy structures of (a) CAl2Be32−, (b) LiCAl2Be3−, (c) CBe5Al−, and (d) CBe5Ga− clusters. The local minimum structures of (e) CBe5In− and (f) CBe5Tl− clusters.
Further, the complete substitution of Al atoms was performed by Castro et al., in which they generated heptaatomic anionic clusters CBe5E− (E = Al, Ga, In, Tl) and searched the PES of the designed systems [63]. For CBe5Al− (Figure 6c) and CBe5Ga− (Figure 6d) clusters, the ppC structures are the global minima. However, for CBe5In− (Figure 6e) and Cbe5Tl− (Figure 6f) clusters, the ppC local minima have only 1.2 kcal mol−1 and 1.8 kcal mol−1 higher energy compared to the lowest-energy isomers, respectively. The geometries show that the ppC atom is present in the middle of the Be4E ring, and an extra Be atom is bonded to one Be–Be bond in the plane. In the case of the CBe5Al− geometry, the aluminum–carbon bond distance is 2.233 Å, which is somewhat lengthier than the normal aluminum–carbon bond length of 2.00 Å and the 2.12 Å values theoretically predicted for the CAl5+ system. The highly negative charges on the carbon are the consequences of the σ-donation from the surrounding atoms. From the valence electronic configuration of the carbon atom, they concluded that the carbon lone pair is donated to the ligand atoms, which assists in stabilizing the planar geometries [63]. The authors found that the planar global minimum geometries are σ- and π-aromatic.
In 2008, Qiong et al. designed CBe5 and CBe54− systems having a ppC atom in their stable local minimum structures (Figure 7a) [64]. The Be5 ring assists as a σ-donor and a π-acceptor in the D5h structure of CBe5 and CBe54− systems, respectively. The NICS calculations predicted that in the D5h structure of CBe5 and CBe54− systems, σ-aromaticity and π-aromaticity, respectively, are dominant. Although the CBe54− cluster has a ppC, the greater charge density makes it unstable. However, the instability of this cluster is resolved by adding Li+ ions to neutralize the negative charges and the resulting species are CBe5Linn−4 (n = 1 to 5) (Figure 7b to 7f, respectively) [65]. In these clusters, the ppC cores are preserved when Li+ ions are bonded with their corresponding anions. The central carbon in the global minimum structures acts as the σ-acceptor and π-donor. The electron delocalization within the CBe5Linn−4 (n = 1 to 5) clusters is predicted from the induced magnetic field analysis. The energy gap between the HOMO and LUMO increases moderately upon increasing the counter ions from CBe5Li3− (3.47 eV) to CBe5Li5+ (7.11 eV), suggesting increased stability following the maximum hardness principle (MHP) [[66],[67]]. The molecular dynamics simulations of the systems at 1000 K for 20 ps show that the CBe5 pentagon remains intact during the entire simulation. The negative charge density on the CBe54− cluster is also decreased by capping H+ ions to the system, just as in the case of Li+ ions, and the species are CBe5Hnn−4 (n = 2–5) [68]. In the case of CBe5H22− (Figure 8a) and CBe5H3− (Figure 8b) clusters, the ppC structures are the lowest-energy C2v point group of symmetry. For the CBe5H4 cluster (Figure 8c), a quasi-planar geometry has 1.8 kcal mol−1 more energy compared to the tetrahedral global minimum structure. Moreover, the CBe5H5+ cluster (Figure 8d) has a quasi-planar ppC structure as the global minimum. The stability of the ppC- or quasi-ppC-containing geometries is governed by the presence of the peripheral three-centered-two-electron Be–H–Be bonds, the origination of the stable eight-electron shell structure, and the presence of the 6σ and 2π dual aromaticity. The excess charge density on the CBe54− system is also reduced by complexing with halogen cations (F+, Cl+, and Br+) or alkali metal cations (Li+, Na+, and K+) to generate CBe5X5+ systems [69]. The PES search shows that the global minima of the clusters are either in ppC or quasi-ppC forms. The global minima of CBe5F5+, CBe5Li5+, CBe5Na5+, and CBe5K5+ clusters have excellently planar and extremely symmetric D5h geometries, whereas CBe5Cl5+ and CBe5Br5+ clusters experience slight non-planar contortion as C2 geometries. Again, in these systems, the three-centered-two-electron Be–X–Be bonds provide stability in planar forms. The NICS analysis proved the double aromatic character (σ- and π-aromaticity) of the systems is in agreement with the adaptive natural density partitioning (AdNDP) analyses [[70],[1]]. The molecular dynamics simulations suggested that the ppC-containing CBe5 ring in the minimum energy structures is well conserved throughout the whole simulation, indicating that the geometries are rigid against isomerization and decomposition.
Chemistry 04 00113 g021 550
Figure 7. (a) The symmetric structures CBe5 and CBe54− are ppC species. The neutral and tetraanionic forms have the same shape but different bond lengths. The global minimum structures of (b) CBe5Li3−, (c) CBe5Li22−, (d) CBe5Li3−, (e) CBe5Li4, and (f) CBe5Li5+ clusters.
Chemistry 04 00113 g022 550
Figure 8. The global minimum structures of (a) CBe5H22− and (b) CBe5H3− clusters with a perfect ppC. The local and global minimum structures of (c) CBe5H4 and (d) CBe5H5+ clusters, respectively, with a quasi-ppC.
In 2018, Zhao et al. reported various ppC systems by adding hydrogen atoms to the CAl4Be, CAl3Be2−, CAl2Be32−, and CAlBe43− parent molecules [71]. They reported nine new planar and quasi-planar ppC clusters of CAlnBemHxq (n + m = 5, q = 0, ±1, x = q + m − 1) (Figure 9). The ppC core remains unchanged geometrically and electronically with the gradual introduction of hydrogen atoms. Interestingly, the energy gap between the HOMO and LUMO increases in the studied clusters as compared to the parent anionic clusters. The presence of the three-centered-two-electron Be–H–Be or Be–H–Al π bonds is responsible for the stabilization of the ppC geometries [71]. Remarkably, among the nine studied clusters, seven molecules show ppC in the global minimum structures. Again, among the global minimum geometries, only CAl3Be2H, CAl2Be3H−, CAl2Be3H2, and CAlBe4H4+ clusters are dynamically stable enough. For the CAl4BeH4+ and CAl3Be2H2+ clusters, the ppC isomers have 10.7 and 3.8 kcal mol−1 higher energy, respectively, with respect to the lowest-energy structures. However, the closest isomers of the CAl3Be2H, CAl2Be3H−, CAl2Be3H2, CAl2Be3H3+, CAlBe4H2−, CAlBe4H3, and CAlBe4H4+ clusters have 4.6, 3.1, 4.6, 3.6, 3.7, 2.8, and 15.0 kcal mol−1 higher energies, respectively, with respect to the global minimum structures [71]. The NICS calculations predicted that the considered clusters are σ- and π-dual aromatic. The natural bond orbital (NBO) computations predicted that there is a significant contribution of the ionic and covalent bonding toward the stabilization of the ppC structures.
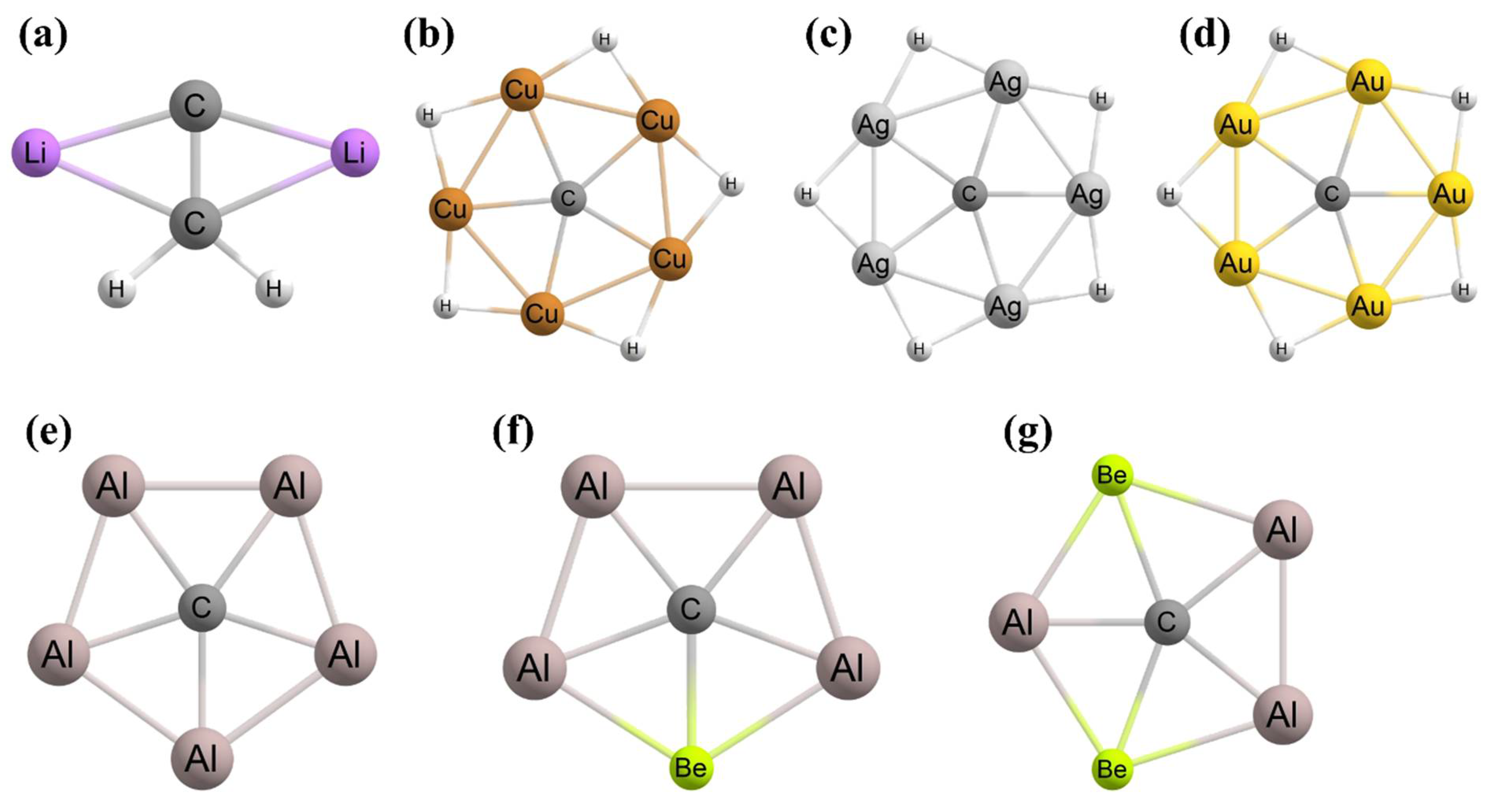
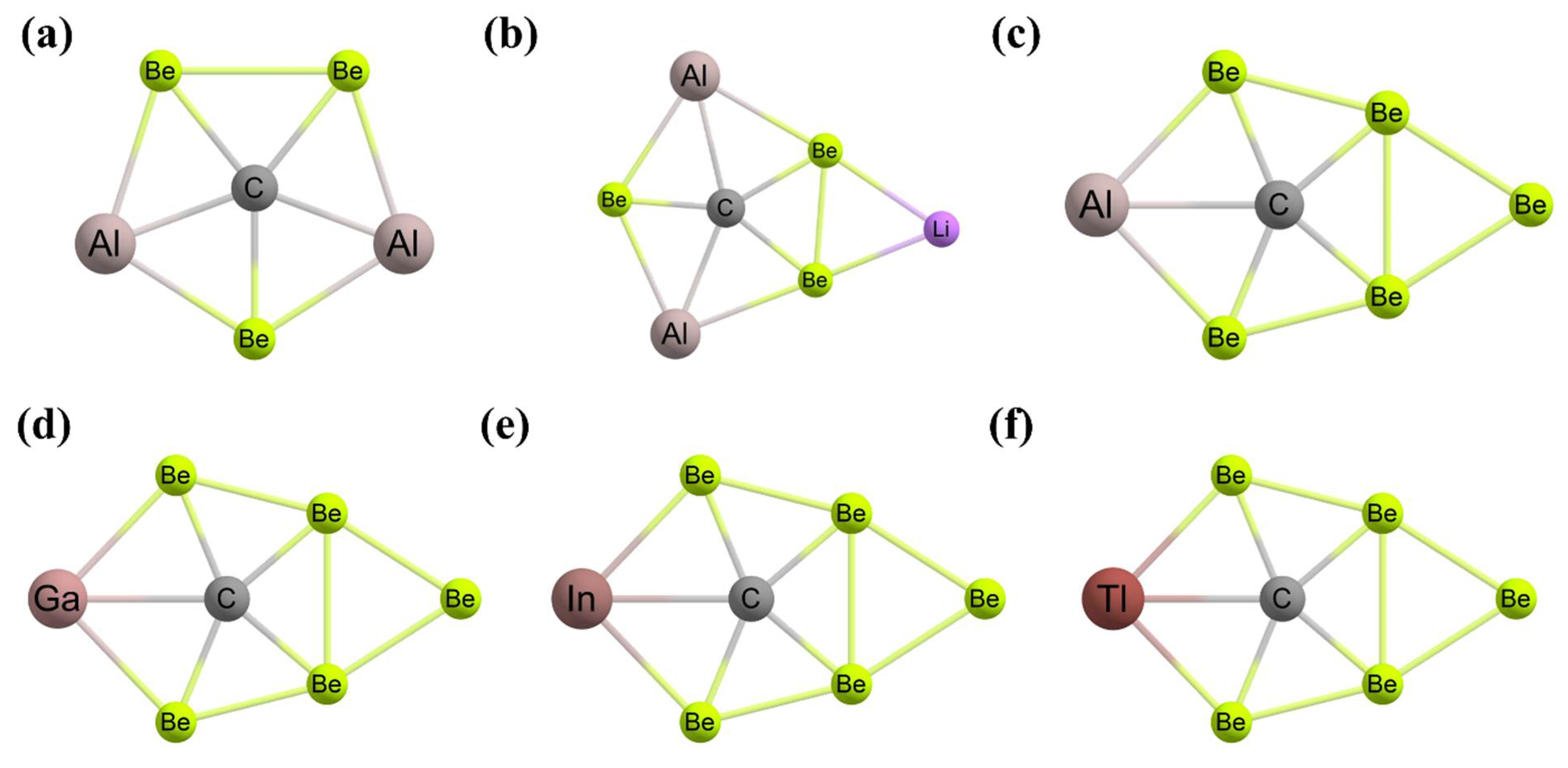
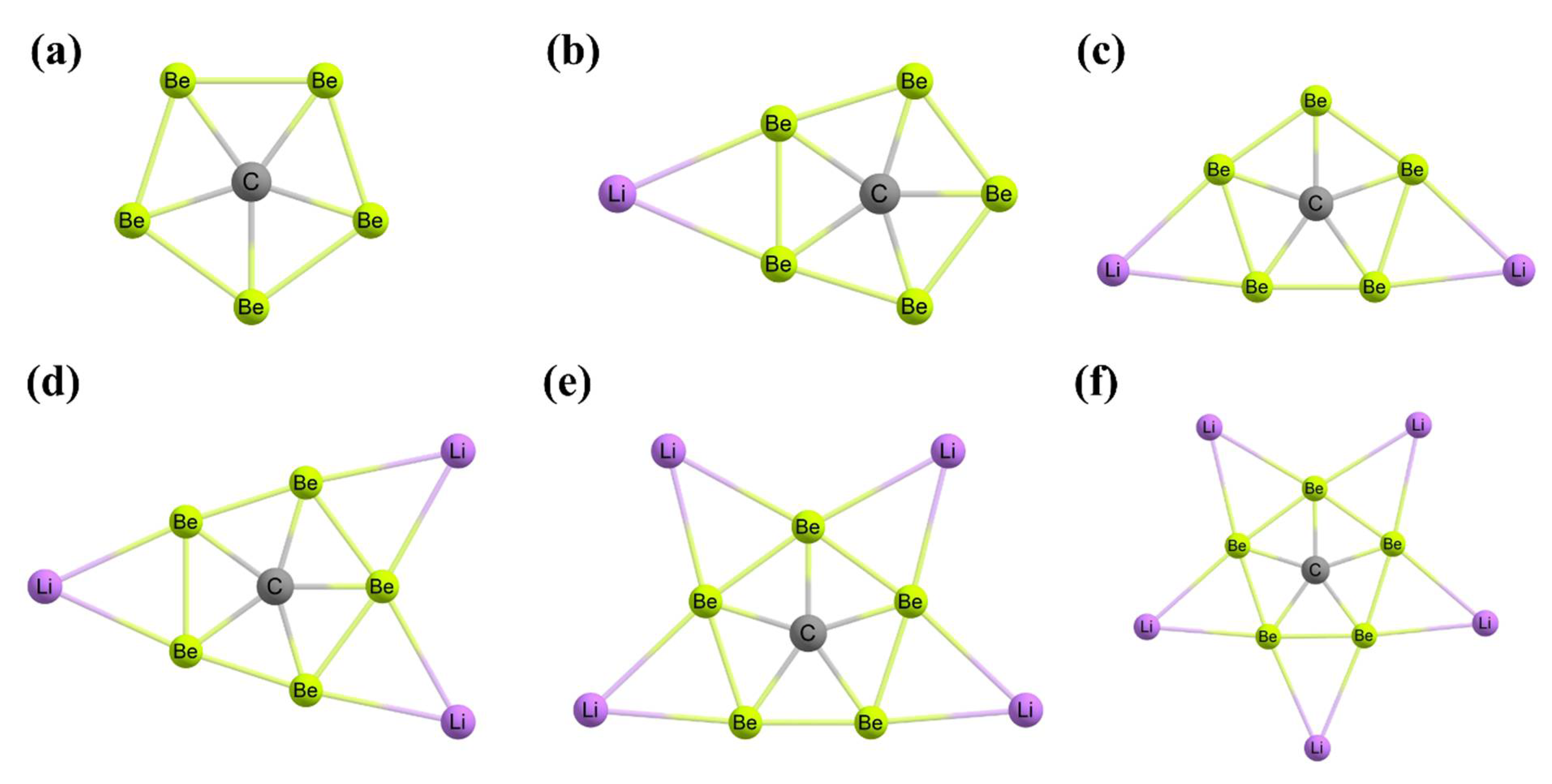
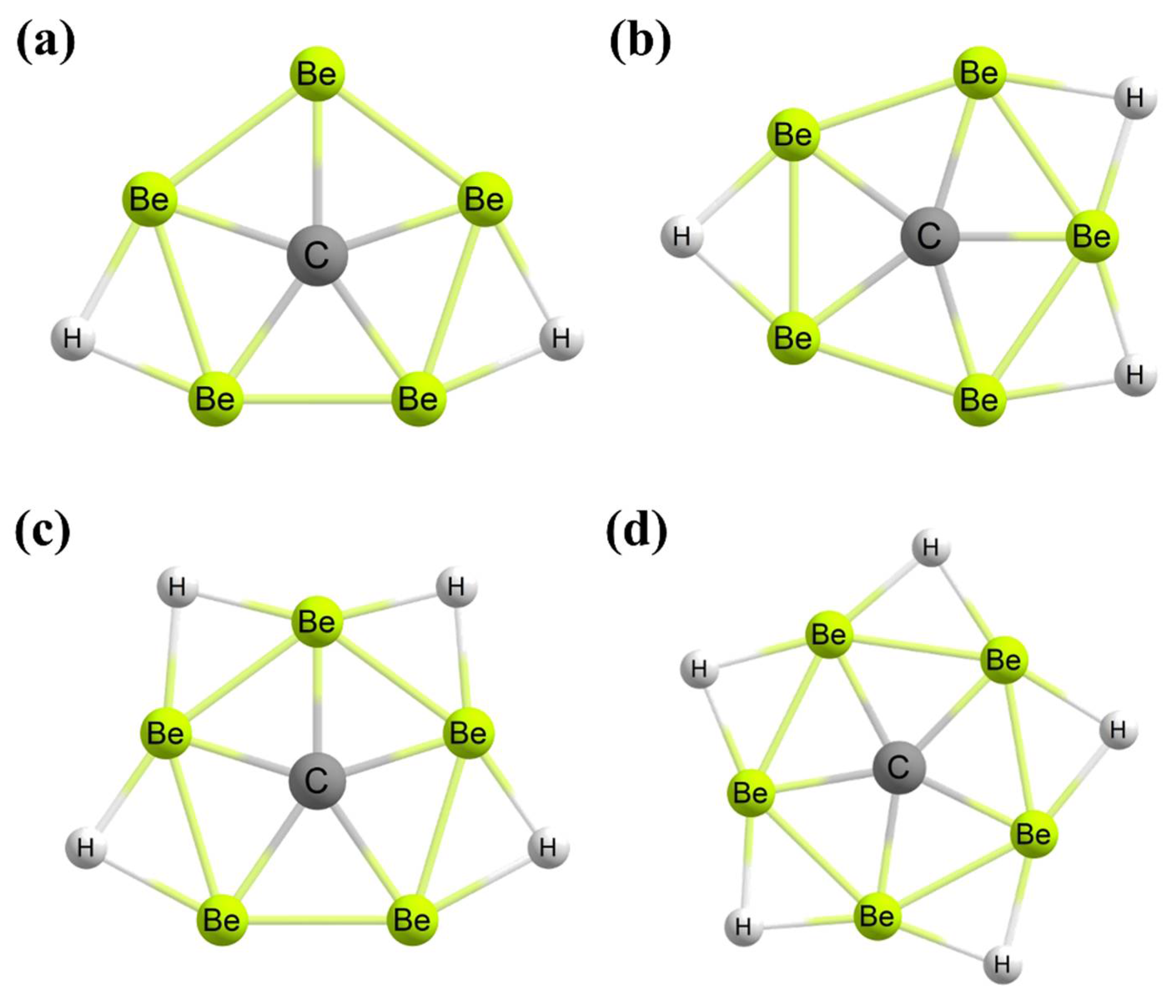
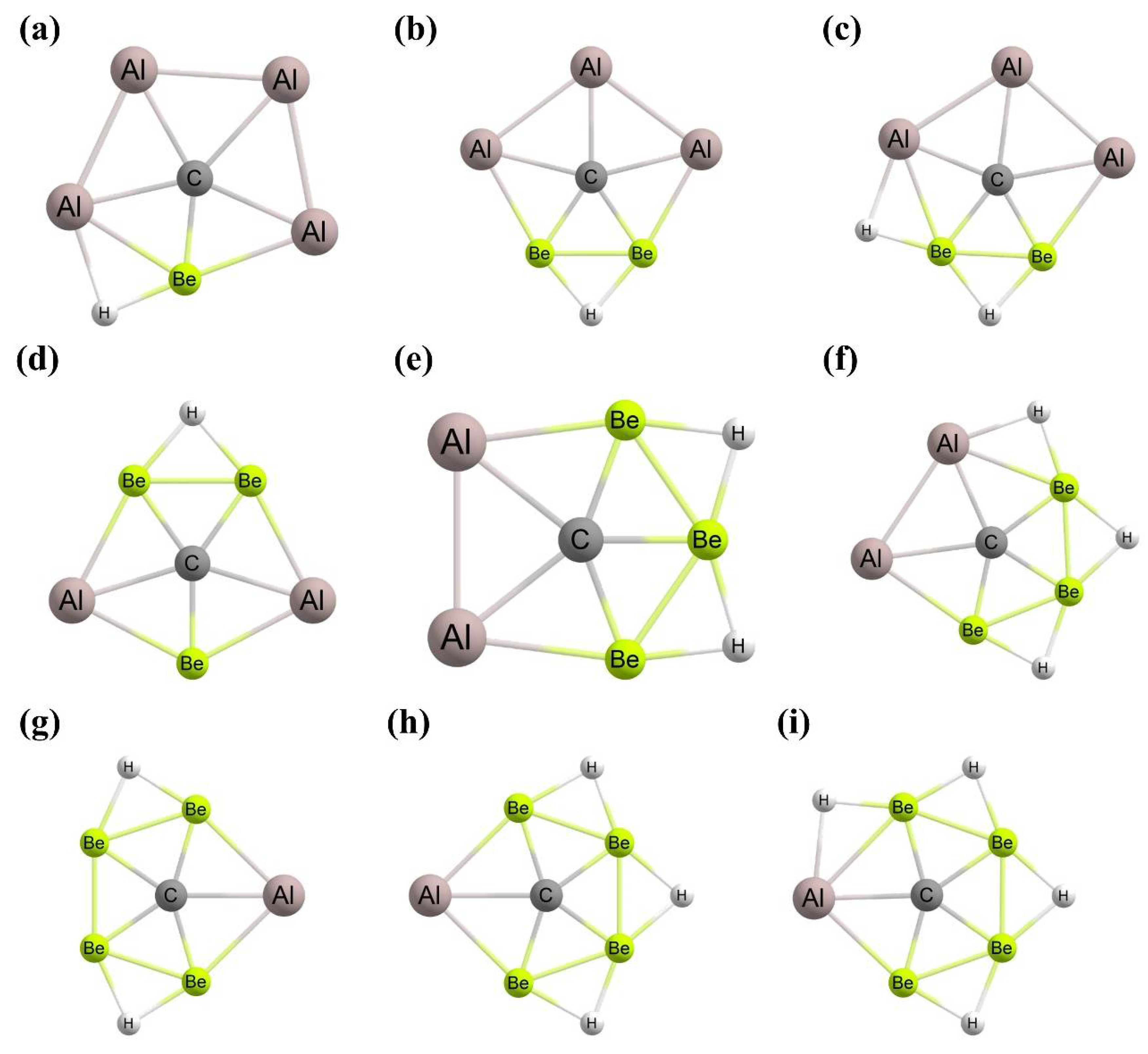
Chemistry 04 00113 g024 550
Figure 9. Optimized structures of (a) CAl4BeH4+, (b) CAl3Be2H, (c) CAl3Be2H2+, (d) CAl2Be3H−, (e) CAl2Be3H2, (f) CAl2Be3H3+, (g) CAlBe4H2−, (h) CAlBe4H3, and (i) CAlBe4H4+ clusters.
Recently, Pan et al. reported a family of systems with ppC based on the next heaviest analogue of the CAl5+ system [72]. As the size of the Ga atom is larger than that of the Al, no ppC isomer is found as a global and/or local minimum for the CGa5+ system. Hence, with the use of the smaller-sized beryllium (Be) atoms, the isoelectronic substitution of Ga atoms generated CGa4Be, CGa3Be2−, CGa2Be32−, and CGaBe43− clusters with ppC in the global minimum structures (Figure 10). For the neutralization of the anionic clusters, one, two, and three Li+ ions were used for CGa3Be2−, CGa2Be32−, and CGaBe43− clusters, respectively, to generate CGa3Be2Li, CGa2Be3Li2, and CGaBe4Li3 clusters (Figure 10). Although the anionic systems have ppC in the global minimum structures, the first ionization potential of CGa2Be32− and CGaBe43− clusters are negative (−2.91 and −6.45 eV, respectively) suggesting the spontaneous loss of an electron from the clusters [72]. However, the first ionization potential of the CGa3Be2− cluster is positive (1.20 eV) indicating its stability towards the spontaneous loss of an electron. The central carbon in the global minimum structures acts as the σ-acceptor and π-donor. Moreover, the extent of π-back-bonding from the 2pz orbital of the central carbon also increases by increasing the number of counter-ions. The electron delocalization within the system is well understood from the molecular orbitals and their magnetic responses studies. The magnetic responses indicated the σ- and π-aromaticity of the global minimum structures, and the σ-contribution is the governing one [72].
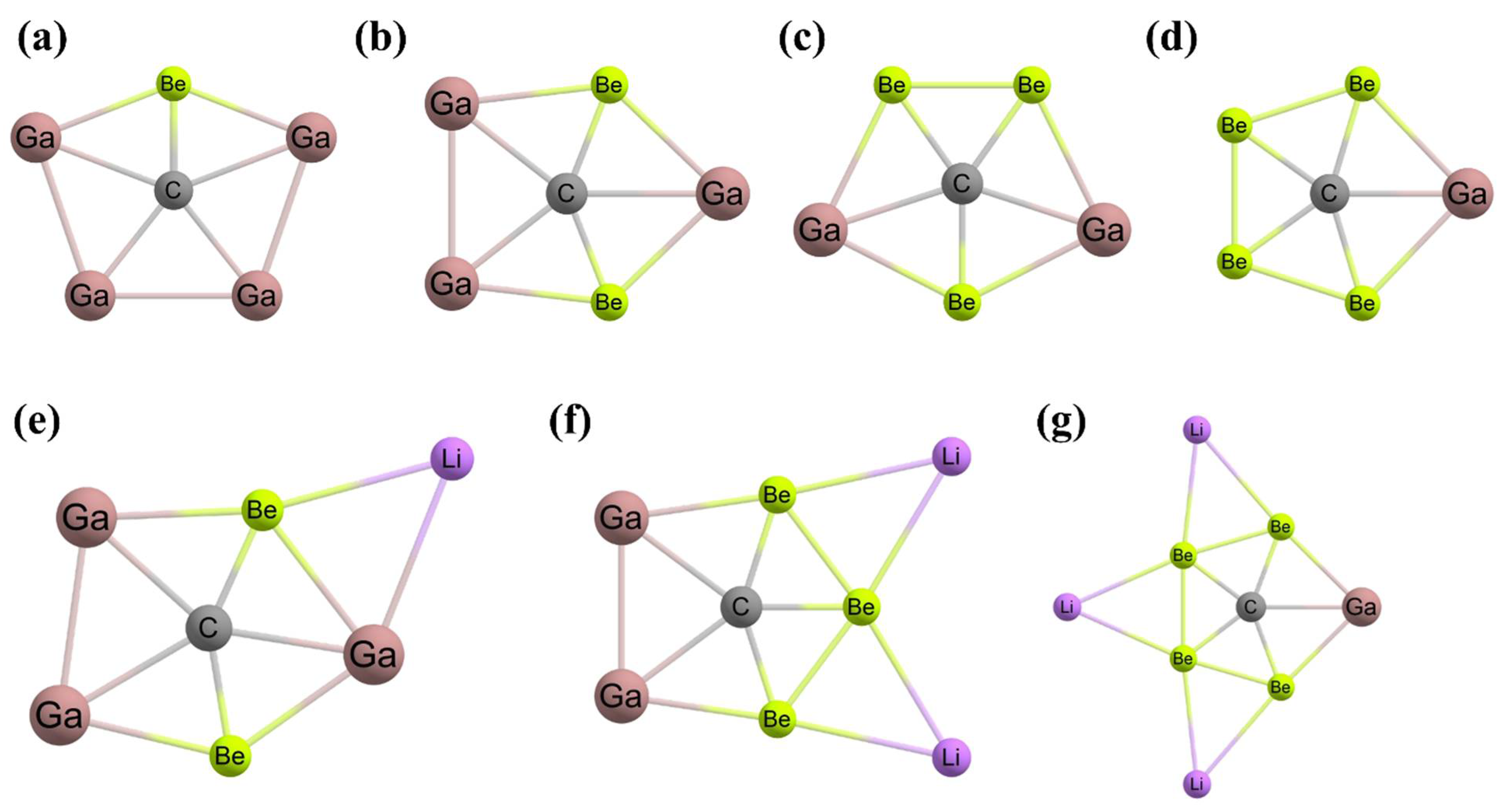
Chemistry 04 00113 g025 550
Figure 10. The lowest-energy ppC forms for (a) CGa4Be, (b) CGa3Be2−, (c) CGa2Be32−, (d) CGaBe43−, (e) CGa3Be2Li, (f) CGa2Be3Li2, and (g) CGaBe4Li3 clusters.
Using silicon (Si) as the surrounding atoms, Zdetsis et al. in 2011 designed Si5C2− and Si5C− clusters (Figure 11a) with the help of the DFT and the coupled-cluster theory that predicted planar structures of the clusters stabilized by the C–Si bonds [73]. These local minimum structures have 12.9 and 22.8 kcal mol−1 higher energy compared to the three-dimensional-type global minimum for Si5C2− and Si5C− clusters, respectively. For the Si5C− cluster, the authors reported two planar structures with D5h and Cs point groups of symmetries that are related by Jahn–Teller distortions. However, these two geometries differ by only 8 kcal mol−1 of energy.
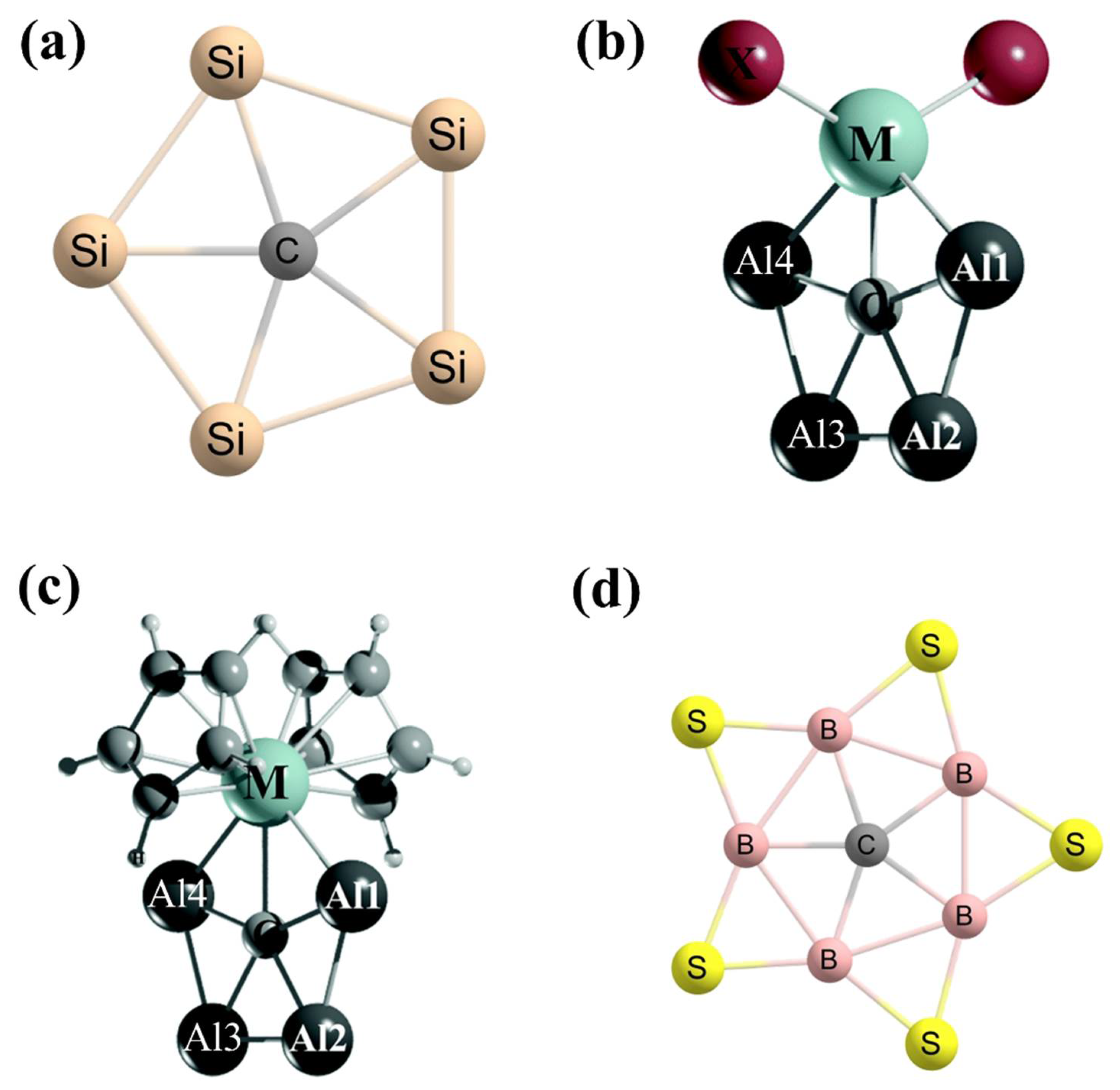
Chemistry 04 00113 g026 550
Figure 11. (a) The symmetric structures Si5C2− and Si5C− clusters are ppC species. The monoanionic and dianionic forms have the same shape but different bond lengths. The lowest-energy isomers of (b) CAl4MX2 clusters and (c) CAl4M(C5H5)2 clusters. The global minimum structure of (d) CB5S5+ cluster with a ppC.
Merino and co-workers used transition metals along with the main group elements to design a ppC in the global minimum structure. They reported CAl4MX2 clusters (M = Zr and Hf; X = F–I and C5H5) with a ppC connected to a transition metal and attached to a metallocene skeleton (Figure 11b,c) [74]. The natural charge analysis suggested that a significant amount of electron transfer occurs from the surrounding atoms to the central carbon atom and the values are in the range of −2.21 to −2.37 |e|. The BOMD simulations assist the kinetic stability of the Zr systems at 700 K.
Very recently, Sun et al. designed a sulfur-surrounded boron wheel CB5S5+ cluster with a ppC in the global minimum structure (Figure 11d) [75]. In this cluster, the presence of the strong π back-donation from the five-bridged sulfur atoms to the boron atoms lowers the electron-deficient nature of the boron centers. The second-lowest isomer with a ptC atom has 1.1 kcal mol−1 higher energy than the lowest-energy ppC isomer. The structure with planar pentacoordinate boron (ppB) has 61.2 kcal mol−1 higher energy than the ppC structure. The BOMD simulation suggested that at 4 K, the global minimum is dynamically very rigid. Moreover, the planarity of the cluster is well conserved at 298 K, 500 K, and 1000 K temperatures. The considered cluster has a 7.47 eV energy gap between HOMO and LUMO, a high VDE value of 13.22 eV, and a low vertical electron affinity (VEA) of 4.31 eV, indicating an electronically robust structure [75]. The NICS computations show the σ + π double aromaticity in the CB5S5+ cluster.
All the above-mentioned global and/or local minimum structures contain one ppC. In 2005, Schleyer and coworkers reported certain fluxional wheel-like species, namely, C2B8, C3B93+, and C5B11+, in which the interior C2, C3, and C5 fragments revolve within the boron rings, respectively (Figure 12) [76]. In C2B8, C3B93+, and C5B11+ species, there are two, three, and five ppC centers that coexist in the energy minimum geometries, respectively. The NICS computations predict the π-aromaticity of these species with more than one ppC atom. These unusual planar clusters are stable when the constituent elements are suited nicely, both geometrically and electronically.
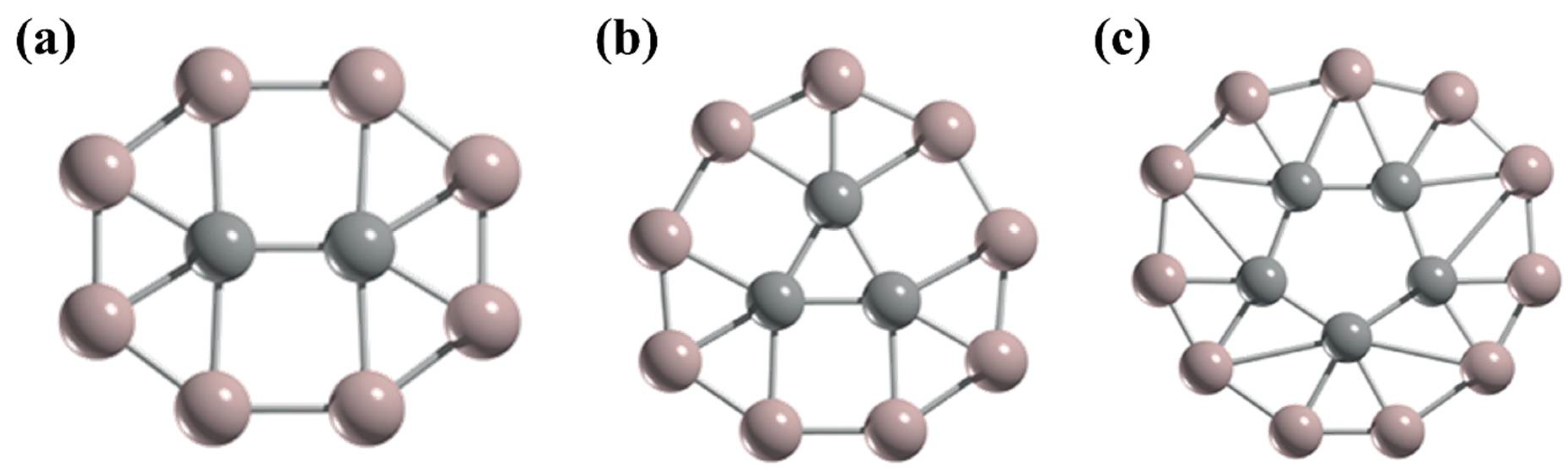
Chemistry 04 00113 g027 550
Figure 12. The boron–carbon clusters (a) C2B8, (b) C3B93+, and (c) C5B11+ are local minimum structures that include conformationally dynamic C2, C3, and C5 units, respectively, within boron rings.

3. Planar Hexacoordinate Carbons (phCs)

The possibility of the ptC and ppC molecules and/or ions are discussed in the previous two sections. Now the question arises of whether it is feasible to obtain a planar hexacoordinate carbon (phC) or a planar heptacoordinate carbon, or a planar octacoordinate carbon. In the case of the main group of components, the existence of planar hexacoordination is limited. Despite various species with hexacoordinate carbon being described, they have 3D geometries (Figure 13) [77][78][79]. In 2000, the first example with a phC is the CB62− di-anionic system (Figure 14a), studied by Exner et al. using DFT and high-level ab initio calculations [80]. This system has a D6h point group of symmetry. The reported structure is not the lowest-energy isomer, rather it is a local minimum with 143.9 kJ mol−1 more energy compared to the lowest-energy structure. This cluster shows benzene-like HOMOs and is aromatic in nature.
Chemistry 04 00113 g028 550
Figure 13. Some compounds with hexacoordinate carbons have three-dimensional structures.
Figure 14. Local minimum structures of (a) CB62− and (b) CN3Be3+ clusters with a phC. Global minimum structures of (c) CO3Li3+ and (d) CE3M3+ (E = S–Te, and M = Li–Cs) clusters.
In 2012, Wu et al. used a CB62− unit and executed isoelectronic replacement on it to compose unipositive CN3Be3+ and CO3Li3+ clusters (Figure 14b and 14c, respectively) [81]. Both clusters in their phC structures correspond to the D3h symmetry. The CN3Be3+ cluster is a local minimum with 25.5 kJ mol−1 more energy with respect to the global minimum geometry. However, the CO3Li3+ cluster is a putative global minimum with a phC center. The authors mentioned that the three bridging Li+ ions stabilized the CO32− ion electrostatically. Later, Leyva-Parra et al. studied the charges on the middle carbon and the bridging Li centers, and the values are 0.87 |e| and 0.97 |e|, respectively [82]. Hence, the positive charges on both carbon and lithium atoms imply electrostatic repulsion between them. Due to this repulsion and the nonappearance of any remarkable orbital overlap between them, this hexacoordinate environment is ambiguous. Because of the different electronegativity values of carbon and oxygen atoms, positive charges on the phC are expected. Therefore, Leyva-Parra et al. substituted the oxygen atoms with the least electronegative sulphur atoms to obtain a true phC atom in the global minimum structures [82]. The fifteen possible CE3M3+ (E=S–Te, and M=Li–Cs) combinations are to be identified as phC clusters (Figure 14d). The natural charge analysis shows negative charges on the phC and positive charges on the bridging metal atoms suggesting electrostatic attractions between the partially negative central carbon atom and partially positive bridged metal atoms. These phC clusters were designed following the so-called “proper polarization of ligand” approach [82]. Through systematic bonding analyses, the authors stated the covalent nature of the C–E bonds and the ionic nature of the C–M bonds.

This entry is adapted from the peer-reviewed paper 10.3390/chemistry4040113

References

  1. Pepper, M.J.; Shavitt, I.; Schleyer, P.v.R.; Glukhovtsev, M.N.; Janoschek, R.; Quack, M. Is the stereomutation of methane possible? J. Comput. Chem. 1995, 16, 207–225.
  2. Golden, D.M.; Walsh, R.; Benson, S.W. The Thermochemistry of the Gas Phase Equilibrium I2 + CH4 CH3I + HI and the Heat of Formation of the Methyl Radical. J. Am. Chem. Soc. 1965, 87, 4053–4057.
  3. Crans, D.C.; Snyder, J.P. Tetracoordinate planar carbon: A singlet biradical. J. Am. Chem. Soc. 1980, 102, 7152–7154.
  4. Schleyer, P.v.R.; Boldyrev, A.I. A new, general strategy for achieving planar tetracoordinate geometries for carbon and other second row periodic elements. J. Chem. Soc. Chem. Commun. 1991, 1536–1538.
  5. Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in Pentaatomic Molecules. J. Am. Chem. Soc. 1998, 120, 7967–7972.
  6. Gribanova, T.N.; Minyaev, R.M.; Minkin, V.I. Planar Tetracoordinate Carbon in Organoboron Compounds: Ab initio Computational Study. Collect. Czech. Chem. Commun. 1999, 64, 1780–1789.
  7. Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038.
  8. Wang, Z.X.; Manojkumar, T.K.; Wannere, C.; Schleyer, P.V.R. A Theoretical Prediction of Potentially Observable Lithium Compounds with Planar Tetracoordinate Carbons. Org. Lett. 2001, 3, 1249–1252.
  9. Wang, Z.X.; Schleyer, P.v.R. A New Strategy To Achieve Perfectly Planar Carbon Tetracoordination. J. Am. Chem. Soc. 2001, 123, 994–995.
  10. Merino, G.; Méndez-Rojas, M.A.; Vela, A. (C5M2-n)n- (M = Li, Na, K, and n = 0, 1, 2). A New Family of Molecules Containing Planar Tetracoordinate Carbons. J. Am. Chem. Soc. 2003, 125, 6026–6027.
  11. Sahin, Y.; Prasang, C.; Hofmann, M.; Subramanian, G.; Geiseler, G.; Massa, W.; Berndt, A. A Diboracyclopropane with a Planar-Tetracoordinate Carbon Atom and a Triborabicyclobutane. Angew. Chem. Int. Ed. 2003, 42, 671–674.
  12. Li, S.D.; Ren, G.M.; Miao, C.Q.; Jin, Z.H. M4H4X: Hydrometals (M=Cu, Ni) Containing Tetracoordinate Planar Nonmetals (X = B, C, N, O). Angew. Chem. Int. Ed. 2004, 43, 1371–1373.
  13. Merino, G.; Méndez-Rojas, M.A.; Beltran, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169.
  14. Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315.
  15. Priyakumar, U.D.; Reddy, A.S.; Sastry, G.N. The design of molecules containing planar tetracoordinate carbon. Tetrahedron Lett. 2004, 45, 2495–2498.
  16. Merino, G.; Méndez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372.
  17. Minkin, V.I.; Gribanova, T.N.; Minkin, V.I.; Starikov, A.G.; Hoffmann, R. Planar and Pyramidal Tetracoordinate Carbon in Organoboron Compounds. J. Org. Chem. 2005, 70, 6693–6704.
  18. Su, M.D. Theoretical Designs for Planar Tetracoordinated Carbon in Cu, Ag, and Au Organometallic Chemistry: A New Target for Synthesis. Inorg. Chem. 2005, 44, 4829–4833.
  19. Li, S.D.; Ren, G.M.; Miao, C.Q. (M4H3X)2B2O2: Hydrometal Complexes (M = Ni, Mg) Containing Double Tetracoordinate Planar Nonmetal Centers (X = C, N). J. Phys. Chem. A 2005, 109, 259–261.
  20. Esteves, P.M.; Ferreira, N.B.P.; Corrêa, R.J. Neutral Structures with a Planar Tetracoordinated Carbon Based on Spiropentadiene Analogues. J. Am. Chem. Soc. 2005, 127, 8680–8685.
  21. Erker, G. Stereochemistry and catalysis with zirconium complexes. Pure Appl. Chem. 1991, 63, 797–806.
  22. Erker, G.; Albrecht, M.; Kruger, C.; Werner, S. Novel synthetic route to hydrocarbyl-bridged dinuclear zirconium/aluminum complexes exhibiting a planar tetracoordinate carbon center. Organometallics 1991, 10, 3791–3793.
  23. Albrecht, M.; Erker, G.; Nolte, M.; Kruger, C. Planar tetracoordinate carbon stabilized in a dimetallic hafnium/aluminium compound: Formation and crystal structure of Cp2HfA1Me2. J. Organomet. Chem. 1992, 427, C21–C25.
  24. Rottger, D.; Erker, G.; Frohlich, R.; Grehl, M.; Silverio, S.J.; Hylakryspin, I.; Gleiter, R. Determination of the Stabilization Energy of Planar-Tetracoordinate Carbon in Dynamic Dinuclear (μ-Hydrocarbyl)bis(zirconocene) Cation Complexes and Detection of an Organometallic Memory Effect in Their Formation. J. Am. Chem. Soc. 1995, 117, 10503–10512.
  25. Rottger, D.; Erker, G.; Frohlich, R. Formation of stable organometallic planar-tetracoordinate carbon compounds containing a cationic (μ-R1CCR2) framework. J. Organomet. Chem. 1996, 518, 221–225.
  26. Rottger, D.; Erker, G.; Frohlich, R.; Kotila, S. Stabilization of a Planar-tetracoordinate Carbon Center in an Organometallic Complex Containing Both a Zirconocene and a Hafnocene Moiety. Chem. Ber. 1996, 129, 1–3.
  27. Schottek, J.; Erker, G.; Frohlich, R. Formation of Metallocene-Stabilized Planar-Tetracoordinate Carbon Compounds by a Protonation Route. Eur. J. Inorg. Chem. 1998, 1998, 551–558.
  28. Choukroun, R.; Donnadieu, B.; Zhao, J.S.; Cassoux, P.; Lepetit, C.; Silvi, B. Synthesis and Characterization of Heterodimetallic Complexes (Cp’ = C5H4t-Bu, C5H4Me). Formation Mechanism and Theoretical (ELF) Evidence for the Existence of Planar Tetracoordinate Carbon (ptC). Organometallics 2000, 19, 1901–1911.
  29. Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic Tetracoordinate Planar Carbon, 2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632.
  30. Hoffmann, R. The theoretical design of novel stabilized systems. Pure Appl. Chem. 1971, 28, 181–194.
  31. Sorger, K.; Schleyer, P.v.R. Planar and inherently non-tetrahedral tetracoordinate carbon: A status report. J. Mol. Struct. THEOCHEM 1995, 338, 317–346.
  32. Röttger, D.; Erker, G. Compounds containing planar-tetracoordinate carbon. Angew. Chem. Int. Ed. 1997, 36, 812–827.
  33. Radom, L.; Rasmussen, D.R. The planar carbon story. Pure Appl. Chem. 1998, 70, 1977–1984.
  34. Erker, G. Using bent metallocenes for stabilizing unusual coordination geometries at carbon. Chem. Soc. Rev. 1999, 28, 307–314.
  35. Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371.
  36. Keese, R. Carbon flatland: planar tetracoordinate carbon and fenestrenes. Chem. Rev. 2006, 106, 4787–4808.
  37. McGrath, M.P.; Radom, L. Alkaplanes: A class of neutral hydrocarbons containing a potentially planar tetracoordinate carbon. J. Am. Chem. Soc. 1993, 115, 3320–3321.
  38. Lyons, J.E.; Rasmussen, D.R.; McGrath, M.P.; Nobes, R.H.; Radom, L. Octaplan: Ein gesättigter Kohlenwasserstoff mit ungewöhnlich niedriger Ionisierungsenergie und einem planar-tetrakoordinierten Kohlenstoffatom im Radikalkation. Angew. Chem. Int. Ed. Engl. 1994, 33, 1667–1668.
  39. Ding, B.W.; Keese, R.; Stoeckli-Evans, H. First Synthesis and Structure of a Tetraazasilafenestrane. Angew. Chem. Int. Ed. 1999, 38, 375–376.
  40. Rasmussen, D.R.; Radom, L. Planar tetrakoordinierter Kohlenstoff in einem neutralen gesättigten Kohlenwasserstoff: Theoretischer Entwurf und Charakterisierung. Angew. Chem. Int. Ed. 1999, 38, 2875–2878.
  41. Wang, Z.X.; Schleyer, P.v.R. The Theoretical Design of Neutral Planar Tetracoordinate Carbon Molecules with C(C)4 Substructures. J. Am. Chem. Soc. 2002, 124, 11979–11982.
  42. Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.v.R.; Seeger, R.; Pople, J.A. Stabilization of Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427.
  43. Cotton, F.A.; Millar, M. The probable existence of a triple bond between two vanadium atoms. J. Am. Chem. Soc. 1977, 99, 7886–7891.
  44. Xie, Y.; Schaefer, H.F. Hexalithiobenzene: A D6h equilibrium geometry with six lithium atoms in bridging positions. Chem. Phys. Lett. 1991, 179, 563–567.
  45. Wang, L.S.; Boldyrev, A.I.; Li, X.; Simons, J. Experimental Observation of Pentaatomic Tetracoordinate Planar Carbon-Containing Molecules. J. Am. Chem. Soc. 2000, 122, 7681–7687.
  46. Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 0114.
  47. Bolton, E.E.; Laidig, W.D.; Schleyer, P.v.R.; Schaefer, H.F. Does singlet 1,1-dilithioethene really prefer a perpendicular structure? J. Phys. Chem. 1995, 99, 17551–17557.
  48. Tsipis, C.A.; Karagiannis, E.E.; Kladou, P.F.; Tsipis, A.C. Aromatic Gold and Silver ‘Rings’: Hydrosilver(I) and Hydrogold(I) Analogues of Aromatic Hydrocarbons. J. Am. Chem. Soc. 2004, 126, 12916–12929.
  49. Tsipis, A.C.; Tsipis, C.A. Hydrometal Analogues of Aromatic Hydrocarbons: A New Class of Cyclic Hydrocoppers(I). J. Am. Chem. Soc. 2003, 125, 1136–1137.
  50. Li, S.D.; Miao, C.Q.; Ren, G.M. D5h Cu5H5X: Pentagonal hydrocopper Cu5H5 containing pentacoordinate planar nonmetal centers (X = B, C, N, O). Eur. J. Inorg. Chem. 2004, 2004, 2232–2234.
  51. Li, S.D.; Guo, Q.L.; Miao, C.Q.; Ren, G.M. Investigation on transition-metal hydrometal complexes MnHnC with planar coordinate carbon centers by density functional theory. Acta Phys. Chim. Sin. 2007, 23, 743–745.
  52. Pei, Y.; An, W.; Ito, K.; Schleyer, P.v.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: A global minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400.
  53. Jimenez-Halla, J.O.C.; Wu, Y.B.; Wang, Z.X.; Islas, R.; Heine, T.; Merino, G. CAl4Be and CAl3Be2−: Global Minima with a Planar Pentacoordinate Carbon Atom. Chem. Commun. 2010, 46, 8776–8778.
  54. Wu, Y.B.; Duan, Y.; Lu, H.G.; Li, S.D. CAl2Be32– and its salt complex LiCAl2Be3–: Anionic global minimawith planar pentacoordinate carbon. J. Phys. Chem. A 2012, 116, 3290–3294.
  55. Castro, A.C.; Martínez-Guajardo, G.; Johnson, T.; Ugalde, J.M.; Wu, Y.B.; Mercero, J.M.; Heine, T.; Donald, K.J.; Merino, G. CBe5E– (E = Al, Ga, In, Tl): Planar pentacoordinate carbon in heptaatomic clusters. Phys. Chem. Chem. Phys. 2012, 14, 14764–14768.
  56. Luo, Q. Theoretical observation of hexaatomic molecules containing pentacoordinate planar carbon. Sci. China, Ser. B Chem. 2008, 51, 1030–1035.
  57. Grande-Aztatzi, R.; Cabellos, J.L.; Islas, R.; Infante, I.; Mercero, J.M.; Restrepo, A.; Merino, G. Planar pentacoordinate carbons in CBe54– derivatives. Phys. Chem. Chem. Phys. 2015, 17, 4620–4624.
  58. Guo, J.C.; Ren, G.M.; Miao, C.Q.; Tian, W.J.; Wu, Y.B.; Wang, X. CBe5Hnn−4 (n = 2–5): Hydrogen-stabilized CBe5 pentagons containing planar or quasi-planar pentacoordinate carbons. J. Phys. Chem. A 2015, 119, 13101–13106.
  59. Guo, J.C.; Tian, W.J.; Wang, Y.J.; Zhao, X.F.; Wu, Y.B.; Zhai, H.J.; Li, S.D. Star-like superalkali cations featuring planar pentacoordinate carbon. J. Chem. Phys. 2016, 144, 244303.
  60. Zhao, X.F.; Bian, J.H.; Huang, F.; Yuan, C.; Wang, Q.; Liu, P.; Li, D.; Wang, X.; Wu, Y.B. Stabilization of beryllium-containing planar pentacoordinate carbon species through attaching hydrogen atoms. RSC Adv. 2018, 8, 36521–36526.
  61. Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar pentacoordinate carbon in CGa5+ derivatives. Phys. Chem. Chem. Phys. 2018, 20, 12350–12355.
  62. Zdetsis, A.D. Novel pentagonal silicon rings and nanowheels stabilized by flat pentacoordinate carbon(s). J. Chem. Phys. 2011, 134, 094312.
  63. Cui, Z.H.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.H.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141.
  64. Sun, R.; Jin, B.; Huo, B.; Yuan, C.; Zhai, H.J.; Wu, Y.B. Planar pentacoordinate carbon in a sulphur-surrounded boron wheel: The global minimum of CB5S5+. Chem. Commun. 2022, 58, 2552–2555.
  65. Erhardt, S.; Frenking, G.; Chen, Z.F.; Schleyer, P.v.R. Aromatic boron wheels with more than one carbon atom in the center: C2B8, C3B93+, and C5B11+. Angew. Chem. Int. Ed. 2005, 44, 1078–1082.
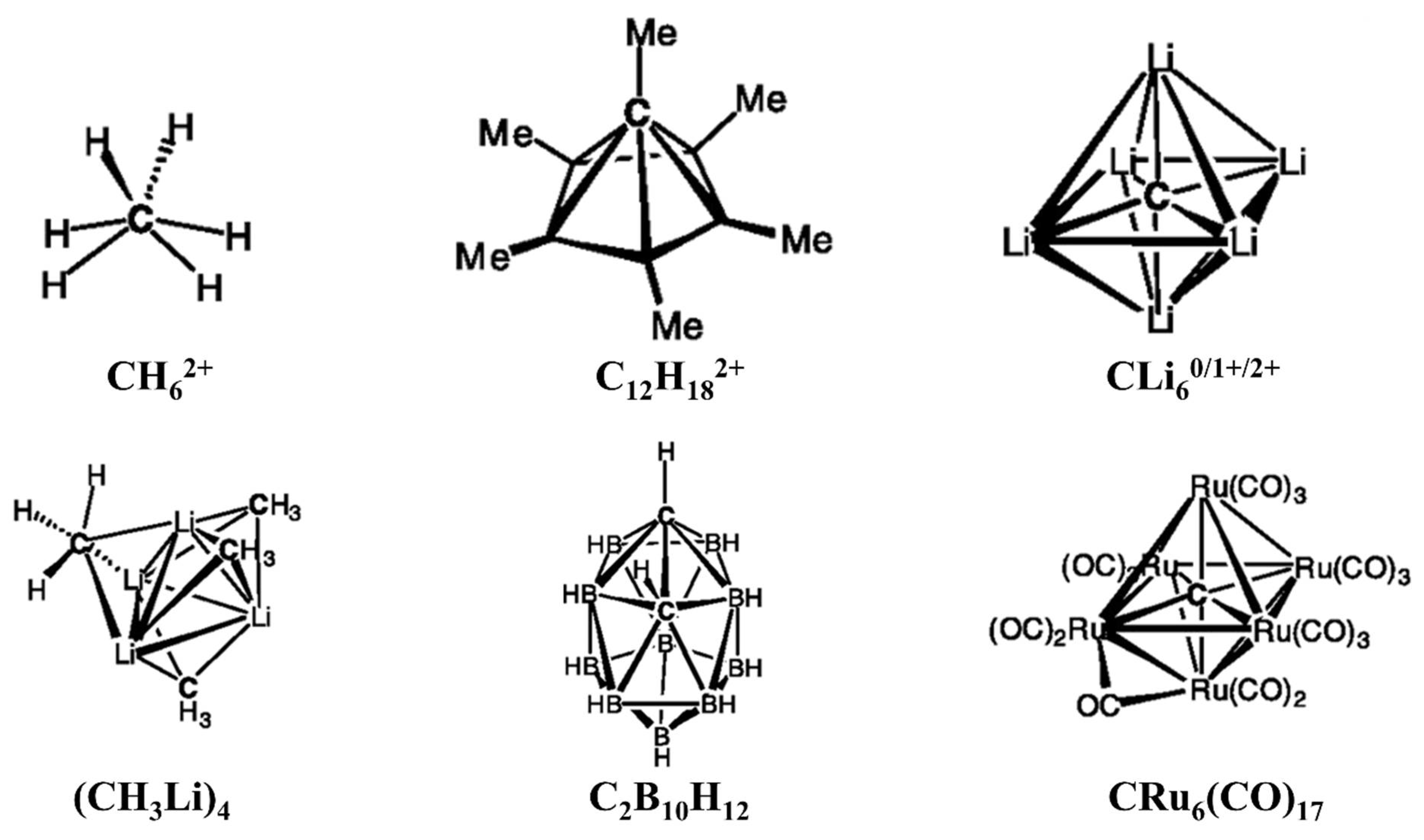
  66. Lammertsma, K.; Barzaghi, M.; Olah, G.A.; Pople, J.A.; Schleyer, P.v.R.; Simonetta, M. Carbodications. 7. Structure and stability of diprotonated methane, CH62+. J. Am. Chem. Soc. 1983, 105, 5258–5263.
  67. Sirigu, A.; Bianchi, M.; Benedetti, E. The crystal structure of Ru6C(CO)17. J. Chem. Soc. D 1969, 596a.
  68. Hogeveen, H.; Kwant, P.W. Pyramidal mono- and dications. Bridge between organic and organometallic chemistry. Acc. Chem. Res. 1975, 8, 413–420.
  69. Exner, K.; Schleyer, P.v.R. Planar Hexacoordinate Carbon: A Viable Possibility. Science 2000, 290, 1937–1940.
  70. Wu, Y.B.; Duan, Y.; Lu, G.; Lu, H.G.; Yang, P.; Schleyer, P.v.R.; Merino, G.; Islas, R.; Wang, Z.X. D3h CN3Be3+ and CO3Li3+: Viable planar hexacoordinate carbon prototypes. Phys. Chem. Chem. Phys. 2012, 14, 14760–14763.
  71. Leyva-Parra, L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar hexacoordinate carbons: Half covalent, half ionic. Angew. Chem. Int. Ed. 2021, 60, 8700–8704.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback