1. Types of Chirality

Chirality describes that something is different from its mirror image. Chirality can be defined in two or three dimensions. It can be an intrinsic property of an object, such as a molecule, crystal or metamaterial. It can also arise from the relative position and orientation of different components, such as the propagation direction of a beam of light relative to the structure of an achiral material.

1.1. Intrinsic 3d Chirality

Any object that cannot be superimposed with its mirror image by translation or rotation in three dimensions has intrinsic 3d chirality. Intrinsic means that the chirality is a property of the object. In most contexts, materials described as chiral have intrinsic 3d chirality. Typical examples are homogeneous/homogenizable chiral materials that have a chiral structure on the subwavelength scale. For example, an isotropic chiral material can comprise a random dispersion of handed molecules or inclusions, such as a liquid consisting of chiral molecules. Handedness can also be present at the macroscopic level in structurally chiral materials. For example, the molecules of cholesteric liquid crystals are randomly positioned but macroscopically they exhibit a helicoidal orientational order. Other examples of structurally chiral materials can be fabricated either as stacks of uniaxial laminas or using sculptured thin films. Remarkably, artificial examples of both types of chiral materials were produced by J. C. Bose more than 11 decades ago.^[1][2] 3D chirality causes the electromagnetic effects of optical activity and linear conversion dichroism.

1.2. Extrinsic 3d Chirality

Any arrangement that cannot be superimposed with its mirror image by translation or rotation in three dimensions has extrinsic 3d chirality. Extrinsic means that the chirality is a consequence of the arrangement of different components, rather than an intrinsic property of the components themself. For example, the propagation direction of a beam of light through an achiral crystal (or metamaterial) can form an experimental arrangement that is different from its mirror image. In particular, oblique incidence onto any planar structure that does not possess two-fold rotational symmetry results in a 3D-chiral experimental arrangement, except for the special case when the structure has a line of mirror symmetry in the plane of incidence.^[3] Bunn^[4] predicted in 1945 that extrinsic 3d chirality would cause optical activity and the effect was later detected in liquid crystals.^[5][6] Extrinsic 3d chirality causes large optical activity and linear conversion dichroism in metamaterials. These effects are inherently tuneable by changing the relative orientation of incident wave and material. Both extrinsic 3d chirality and the resulting optical activity are reversed for opposite angles of incidence.^[7]

1.3. Intrinsic 2d Chirality

Any object that cannot be superimposed with its mirror image by translation or rotation in two dimensions has intrinsic 2d chirality, also known as planar chirality. Intrinsic means that the chirality is a property of the object. Any planar pattern that does not have a line of mirror symmetry is 2d-chiral, and examples include flat spirals and letters such as S, G, P. In contrast to 3d-chiral objects, the perceived sense of twist of 2d-chiral patterns is reversed for opposite directions of observation.^[8] 2d chirality is associated with circular conversion dichroism, which causes directionally asymmetric transmission (reflection and absorption) of circularly polarized electromagnetic waves.

1.4. Extrinsic 2d Chirality

Also 2d chirality can arise from the relative arrangement of different (achiral) components. In particular, oblique illumination of any planar periodic structure will result in extrinsic 2d chirality, except for the special cases where the plane of incidence is either parallel or perpendicular to a line of mirror symmetry of the structure. Strong circular conversion dichroism due to extrinsic 2d chirality has been observed in metamaterials.^[9]

2. Handedness of Electromagnetic Waves

Diagram of electromagnetic wave from a dipole antenna. The orientation of electric vector and the orientation of magnetic vector, is specific as well as chiral. The diagram is non-superposible with its mirror-image. https://handwiki.org/wiki/index.php?curid=1488595

Linearly polarized light. The block of vectors represent how the magnitude and direction of the electric field is constant for an entire plane, which is perpendicular to the direction of travel. https://handwiki.org/wiki/index.php?curid=2028126

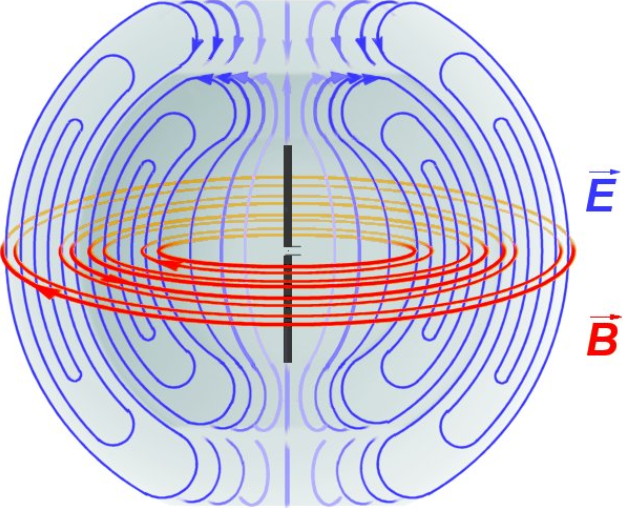
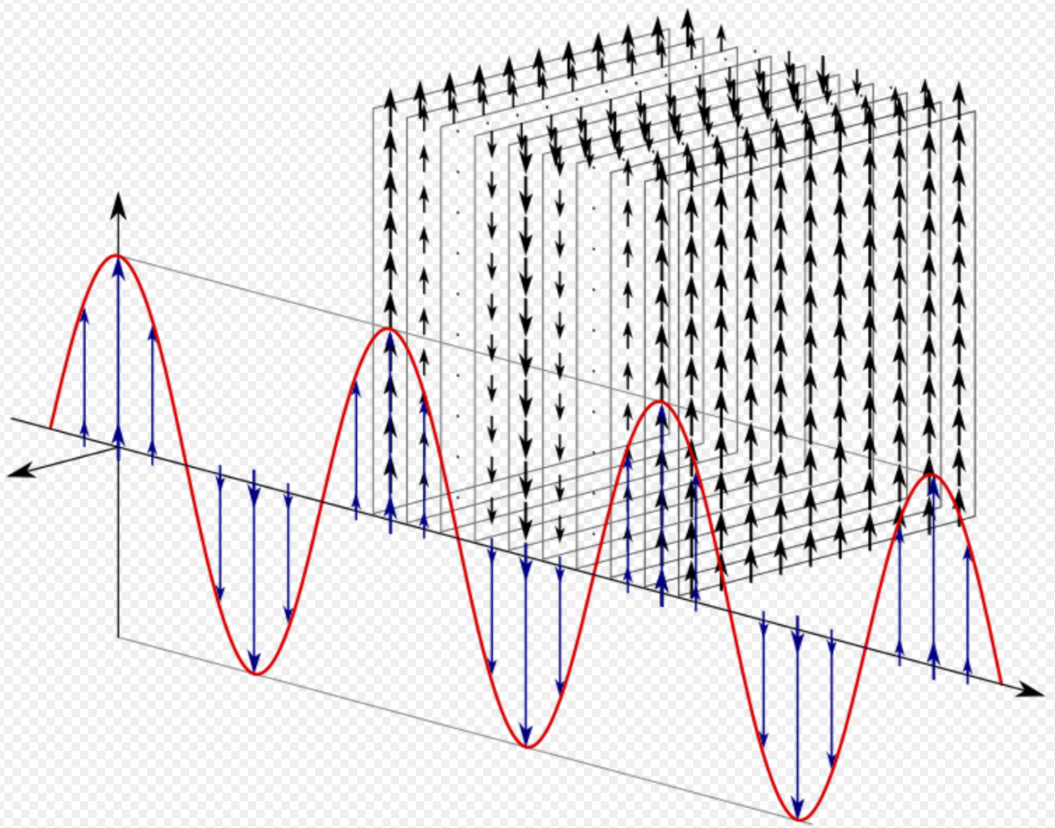
left|200px|Animation of linearly polarized electromagnetic wave, illustrating the directional relationship of the E electric and B magnetic vectors relative to the direction of wave propagation.

Electromagnetic waves can have handedness associated with their polarization. Polarization of an electromagnetic wave is the property that describes the orientation, i.e., the time-varying direction and amplitude, of the electric field vector. For example, the electric field vectors of left-handed or right-handed circularly polarized waves form helices of opposite handedness in space as illustrated by the adjacent animation. Polarizations are described in terms of the figures traced by the electric field vector as a function of time at a fixed position in space. In general, polarization is elliptical and is traced in a clockwise or counterclockwise sense. If, however, the major and minor axes of the ellipse are equal, then the polarization is said to be circular . If the minor axis of the ellipse is zero, the polarization is said to be linear. Rotation of the electric vector in a clockwise sense is designated right-hand polarization, and rotation in a counterclockwise sense is designated left-hand polarization. When deciding whether the rotation is clockwise or counterclockwise, a convention is needed. Optical physicists tend to determine handedness from the perspective of an observer looking towards the source from within the wave, like an astronomer looking at a star. Engineers tend to determine handedness looking along the wave from behind the source, like an engineer standing behind a radiating antenna. Both conventions yield opposite definitions of left-handed and right-handed polarizations and therefore care must be taken to understand which convention is being followed.

Mathematically, an elliptically polarized wave may be described as the vector sum of two waves of equal wavelength but unequal amplitude, and in quadrature (having their respective electric vectors at right angles and π/2 radians out of phase).^[10][11]

2.1. Circular Polarization

Circular polarization, regarding electromagnetic wave propagation, is polarization such that the tip of the electric field vector describes a helix. The magnitude of the electric field vector is constant. The projection of the tip of the electric field vector upon any fixed plane intersecting, and normal to, the direction of propagation, describes a circle. A circularly polarized wave may be resolved into two linearly polarized waves in phase quadrature with their planes of polarization at right angles to each other. Circular polarization may be referred to as "right-hand" or "left-hand," depending on whether the helix describes the thread of a right-hand or left-hand screw, respectively^[12]

3. Optical Activity

3D-chiral materials can exhibit optical activity, which manifests itself as circular birefringence, causing polarization rotation for linearly polarized waves, and circular dichroism, causing different attenuation of left- and right-handed circularly polarized waves. The former can be exploited to realize polarization rotators, while the latter can be used to realize circular polarizers. Optical activity is weak in natural chiral materials, but it can be enhanced by orders of magnitude in an artificial chiral materials, i.e., chiral metamaterials.^{[13] [14] [15] [16]} Just like the perceived sense of twist of a helix is the same for opposite directions of observation, optical activity is the same for opposite directions of wave propagation.

3.1. Circular Birefringence

In 3d-chiral media, circularly polarized electromagnetic waves of opposite handedness can propagate with different speed. This phenomenon is known as circular birefringence and described by different real parts of refractive indices for left- and right-handed circularly polarized waves. As a consequence, left- and right-handed circularly polarized waves accumulate different amounts of phase upon propagation through a chiral medium. This phase difference causes rotation of the polarization state of linearly polarized waves, which may be thought of as superposition of left- and right-handed circularly polarized waves. Circular birefringence can yield a negative index of refraction for waves of one handedness when the effect is sufficiently large.^{[17] [18]}

3.2. Circular Dichroism

In 3d-chiral media, circularly polarized electromagnetic waves of opposite handedness can propagate with different losses. This phenomenon is known as circular dichroism and described by different imaginary parts of refractive indices for left- and right-handed circularly polarized waves.

3.3. Specular Optical Activity

While optical activity is normally observed for transmitted light, polarization rotation^[19] and different attenuation of left-handed and right-handed circularly polarized waves ^[20] can also occur for light reflected by chiral substances. These phenomena of specular circular birefringence and specular circular dichroism are jointly known as specular optical activity. Specular optical activity is weak in natural materials. Extrinsic 3d chirality associated with oblique illumination of metasurfaces lacking two-fold rotational symmetry leads to large specular optical activity.^[21]

3.4. Nonlinear Optical Activity

Optical activity that depends on the intensity of light has been predicted^[22] and then observed in lithium iodate crystals.^[23] In comparison to lithium iodate, extrinsic 3d chirality associated with oblique illumination of metasurfaces lacking two-fold rotational symmetry was found to lead to 30 million times stronger nonlinear optical activity in the optical part of the spectrum.^[24] At microwave frequencies, a 12 orders of magnitude stronger effect than in lithium iodate was observed for an intrinsically 3d-chiral structure.^[25]

4. Circular Conversion Dichroism

2D chirality is associated with directionally asymmetric transmission (reflection and absorption) of circularly polarized electromagnetic waves. 2D-chiral materials, which are also anisotropic and lossy exhibit different total transmission (reflection and absorption) levels for the same circularly polarized wave incident on their front and back. The asymmetric transmission phenomenon arises from different, e.g. left-to-right, circular polarization conversion efficiencies for opposite propagation directions of the incident wave and therefore the effect is referred to as circular conversion dichroism. Like the twist of a 2d-chiral pattern appears reversed for opposite directions of observation, 2d-chiral materials have interchanged properties for left-handed and right-handed circularly polarized waves that are incident on their front and back. In particular left-handed and right-handed circularly polarized waves experience opposite directional transmission (reflection and absorption) asymmetries.^[26][27]

Circular conversion dichroism with almost ideal efficiency has been achieved in metamaterial-based chiral mirrors. In contrast to conventional mirrors, a chiral mirror reflects circularly polarized waves of one handedness without handedness change, while absorbing circularly polarized waves of the other handedness. Chiral mirrors can be realized by placing a 2d-chiral metamaterial in front of a conventional mirror.^[28] The concept has been exploited in holography to realize independent holograms for left-handed and right-handed circularly polarized electromagnetic waves.^[29] Active chiral mirrors that can be switched between left and right, or chiral mirror and conventional mirror, have been reported.^[30]

5. Linear Conversion Dichroism

3D chirality of anisotropic structures is associated with directionally asymmetric transmission (reflection and absorption) of linearly polarized electromagnetic waves. Different levels of total transmission (reflection and absorption) for the same linearly polarized wave incident on their front and back arise from different, e.g. x-to-y, linear polarization conversion efficiencies for opposite propagation directions of the incident wave and therefore the effect is referred to as linear conversion dichroism. The x-to-y and y-to-x polarization conversion efficiencies are interchanged for opposite directions of wave propagation. Linear conversion dichroism has been observed in metamaterials with intrinsic^[31] and extrinsic^[32] 3d chirality. Active metamaterials, where the effect can be turned on and off have been realized by controlling 3d chirality with phase transitions.^[33]

The content is sourced from: https://handwiki.org/wiki/Physics:Chirality_(electromagnetism)