1. History

The channelling effect was first discovered in binary collision approximation computer simulations in 1963^[1] to explain exponential tails in experimentally observed ion range distributions that did not conform to standard theories of ion penetration. The simulated prediction was confirmed experimentally the following year by measurements of ion penetration depths in single-crystalline tungsten.^[2] First transmission experiments of ions channelling through crystals were performed by Oak Ridge National Laboratory group showing that ions distribution is determinated by crystal rainbow channelling effect.^[3]

Fig. 1. An about 12 nm thick silicon crystal viewed down the 110 crystal direction. https://handwiki.org/wiki/index.php?curid=1571428

Fig. 2. Same Si crystal as in Fig. 1 viewed from a randomly rotated direction. https://handwiki.org/wiki/index.php?curid=1632827

2. Mechanism

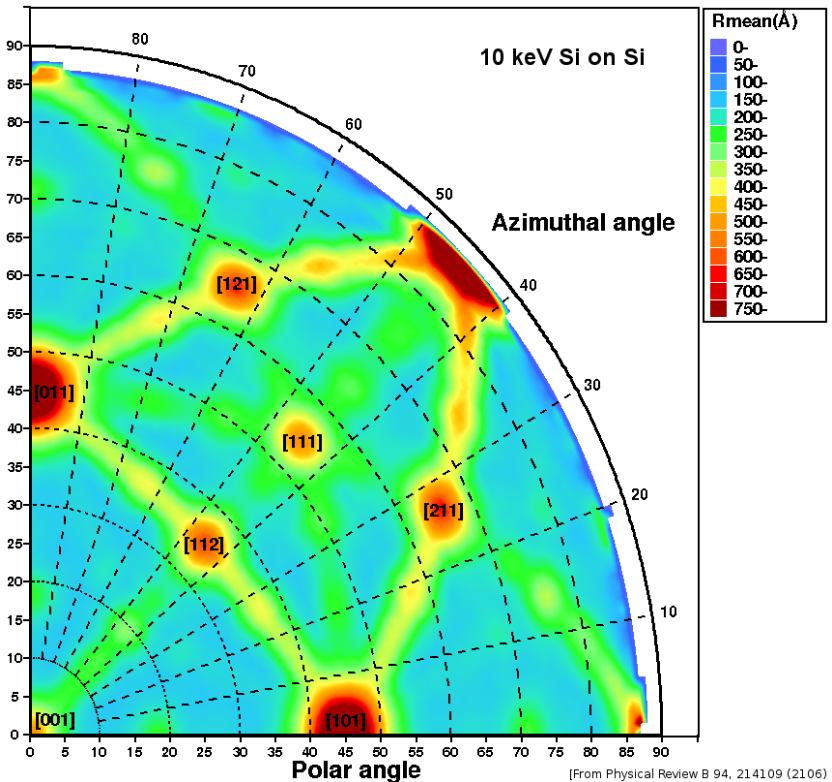
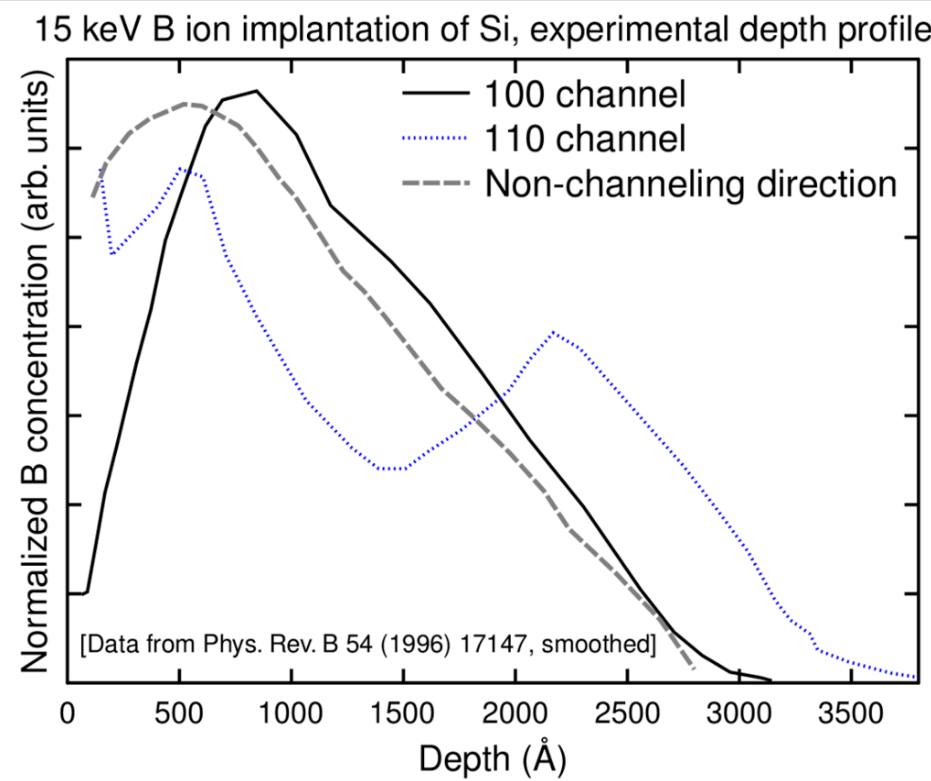
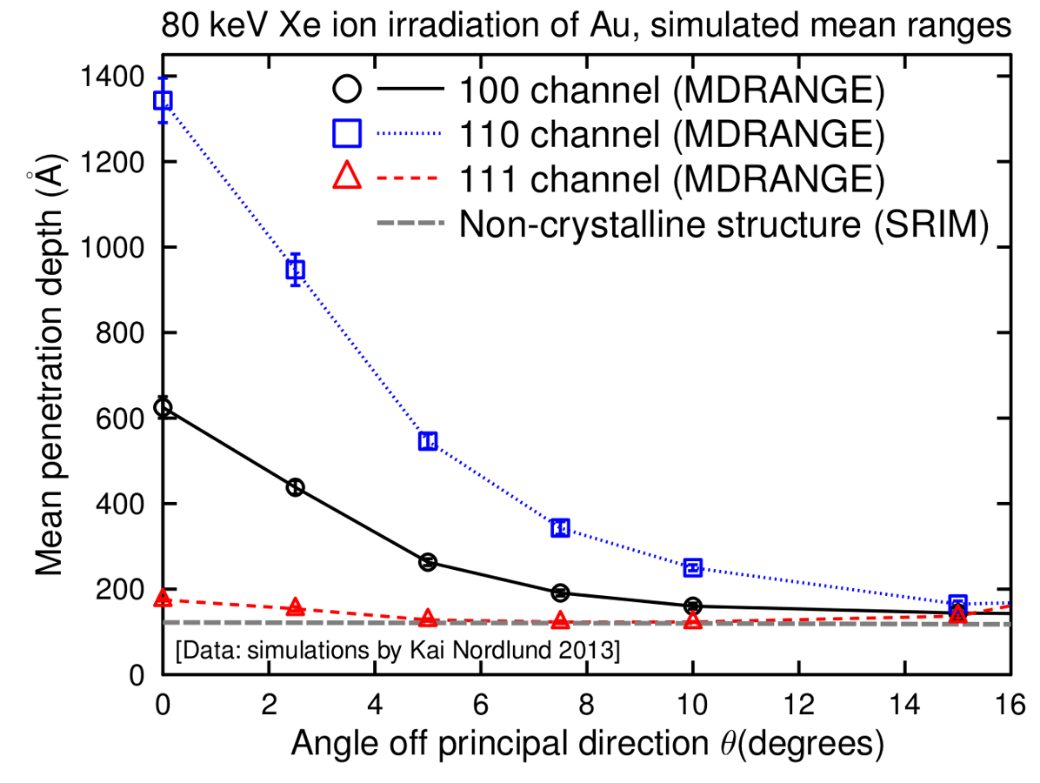
From a simple, classical standpoint, one may qualitatively understand the channelling effect as follows: If the direction of a charged particle incident upon the surface of a monocrystal lies close to a major crystal direction (Fig. 1), the particle with high probability will only do small-angle scattering as it passes through the several layers of atoms in the crystal and hence remain in the same crystal 'channel'. If it is not in a major crystal direction or plane ("random direction", Fig. 2), it is much more likely to undergo large-angle scattering and hence its final mean penetration depth is likely to be shorter. If the direction of the particle's momentum is close to the crystalline plane, but it is not close to major crystalline axes, this phenomenon is called "planar channelling". Channelling usually leads to deeper penetration of the ions in the material, an effect that has been observed experimentally and in computer simulations, see Figures 3-5.^[4]

Negatively charged particles like antiprotons and electrons are attracted towards the positively charged nuclei of the plane, and after passing the center of the plane, they will be attracted again, so negatively charged particles tend to follow the direction of one crystalline plane.

Fig. 3. Map of channelling crystal directions for 10 keV Si ions in Si.^[5] The red and yellow colors indicate directions with deeper mean ion penetration depth, i.e. directions where the ions are channeled. https://handwiki.org/wiki/index.php?curid=1330026

Fig. 4. Experimentally determined penetration depth profiles for 15 keV B ions in Si along the 100 and 110 crystal channels, as well as in a non-channelling direction. The data is scanned in with smoothing from. Ref.^[6] https://handwiki.org/wiki/index.php?curid=1469755

Fig. 5. Computer simulations of the mean penetration depth of 80 keV Xe ion penetration in single crystal Au, considering a tilting of the implantation profile off the main direction. These simulations were made with the MDRANGE code ^[7] for a study of Xe irradiation of Au nanowires.^[8] Also shown are simulations using the binary collision approximation SRIM code which does not take into account the crystal structure and thus does not describe channelling at all. The order of the strength of channelling, i.e. that 110 has the strongest effect, 100 is intermediate and 111 has the weakest, agrees with experimental observations in face-centered cubic metals.^[9] https://handwiki.org/wiki/index.php?curid=1591398 

Because the crystalline plane has a high density of atomic electrons and nuclei, the channeled particles eventually suffer a high angle Rutherford scattering or energy-losses in collision with electrons and leave the channel. This is called the "dechannelling" process.

Positively charged particles like protons and positrons are instead repelled from the nuclei of the plane, and after entering the space between two neighboring planes, they will be repelled from the second plane. So positively charged particles tend to follow the direction between two neighboring crystalline planes, but at the largest possible distance from each of them. Therefore, the positively charged particles have a smaller probability of interacting with the nuclei and electrons of the planes (smaller "dechannelling" effect) and travel longer distances.

The same phenomena occur when the direction of momentum of the charged particles lies close to a major crystalline, high-symmetry axis. This phenomenon is called "axial channelling".

At low energies the channelling effects in crystals are not present because small-angle scattering at low energies requires large impact parameters, which become bigger than interplanar distances. The particle's diffraction is dominating here. At high energies the quantum effects and diffraction are less effective and the channelling effect is present.

3. Applications

There are several particularly interesting applications of the channelling effects.

Channelling effects can be used as tools to investigate the properties of the crystal lattice and of its perturbations (like doping) in the bulk region that is not accessible to X-rays. The channelling method may be utilized to detect the geometrical location of interstitials. This is an important variation of the Rutherford backscattering ion beam analysis technique, commonly called Rutherford backscattering/channelling (RBS-C).

The channelling may even be used for superfocusing of ion beam, to be employed for sub-atomic microscopy.^[10]

At higher energies (tens of GeV), the applications include the channelling radiation for enhanced production of high energy gamma rays, and the use of bent crystals for extraction of particles from the halo of the circulating beam in a particle accelerator.

4. Classical Channelling Theory

The classical treatment of channelling phenomenon supposes that the ion - nucleus interactions are not correlated phenomena. The first analytic classical treatise is due to Jens Lindhard in 1965, who proposed a treatment that still remains the reference one. He proposed a model that is based on the effects of a continuous repulsive potential generated by atomic nuclei lines or planes, arranged neatly in a crystal. The continuous potential is the average in a row or on an atomic plane of the single Coulomb potentials of the charged nuclei [math]\displaystyle{ eZ_2 }[/math] and shielded from the electronic cloud.

The proposed potential (named Lindhard potential) is:

[math]\displaystyle{ V(r) = Z_1Z_2 e^2 \left ( \frac{1}{r} - \frac{1}{\sqrt{r^2+C^2a^2}}\right) }[/math]

r represents the distance from the nucleus, [math]\displaystyle{ C^2 }[/math] is a constant equal to 3 and a is the screen radius of Thomas-Fermi:

[math]\displaystyle{ a = \frac{0.885~a_0}{(\sqrt{Z_1}+\sqrt{Z_2})^{2/3}} }[/math]

[math]\displaystyle{ a_0 }[/math] is equal to the Bohr radius (=0.53Å the radius of the smallest orbit of the Bohr atom). The typical values for the screen radius is in between 0.1-0.2 Å.

Considering the case of axial channelling, if d is the distance between two successive atoms of an atomic row, the mean of the potential along this row is equal to:

[math]\displaystyle{ U_a(\rho)=\frac{1}{d} \int_{-d/2}^{d/2} V \left (\sqrt{z^2+\rho^2}\right) ~\mathrm{d}z = \frac{Z_1Z_2e^2}{d}~\ln \left( \left(\frac{C_a}{\rho}\right)^2+1\right) }[/math]

[math]\displaystyle{ \rho }[/math] equal to the distance between atomic lines. The obtained potential is a continuous potential generated by a string of atoms with an atomic number [math]\displaystyle{ Z_2 }[/math] and a mean distance d between nuclei.

The energy of the channeled ions, having an atomic number [math]\displaystyle{ Z_1 }[/math] can be written as:

[math]\displaystyle{ E=\frac{p_\shortparallel^2}{2M}+\frac{p_\perp^2}{2M}+ U_a(\rho) - U_{\rm min} }[/math]

where [math]\displaystyle{ p_\shortparallel }[/math] e [math]\displaystyle{ p_\perp }[/math]are respectively the parallel and perpendicular components of the momentum of the projectile with respect to the considered direction of the string of atoms. The potential [math]\displaystyle{ U_{\rm min} }[/math] is the minimum potential of the channel, taking into account the superposition of the potentials generated by the various atomic lines inside the crystal.

It therefore follows that the components of the momentum are:

[math]\displaystyle{ p_\perp =p \sin\psi ,~~ p_\shortparallel=p \cos\psi }[/math]

where [math]\displaystyle{ \psi }[/math] is the angle between the direction of motion of an ion and the considered crystallographic axial direction.

Neglecting the energy loss processes, the quantity[math]\displaystyle{ \frac{p_\shortparallel^2}{2M} }[/math] is conserved during the channeled ion motion and the energy conservation can be formulated as follows:

[math]\displaystyle{ E_\perp=\frac{p_\perp^2}{2M}+U_a(\rho)-U_{\rm min}=\frac{p^2 \sin^2(\psi)}{2M}+U_a(\rho)-U_{\rm min} }[/math]

The equation is also known as the expression of the conservation of transverse energy. The approximation of [math]\displaystyle{ \sin(\psi)\approx \psi }[/math] is feasible, since we consider a good alignment between ion and crystallographic axis.

The channelling condition can now be considered the condition for which an ion is channeled if its transverse energy is not sufficient to overcome the height of the potential barrier created by the strings of ordered nuclei. It is therefore useful to define the "critical energy" [math]\displaystyle{ E_c }[/math] as that transverse energy under which an ion is channeled, while if it exceeds it, an ion will be de-channeled.

[math]\displaystyle{ U_a(\rho_c)- U_{\rm min}=E_c }[/math]

Typical [math]\displaystyle{ E_c }[/math] values are a few tens of eV, since the critical distance [math]\displaystyle{ \rho_c }[/math] is similar to the screen radius, i.e. 0.1-0.2 Å. Therefore, all ions with transverse energy lower than [math]\displaystyle{ E_c }[/math] will be channeled.

In the case of [math]\displaystyle{ \psi_0=0 }[/math] (perfect ion-axis alignment) all ions with impact parameter [math]\displaystyle{ \rho \lt \rho_{\rm c} }[/math] will be de-channeled.

[math]\displaystyle{ \chi_{\rm min}=\frac{\pi \rho_{\rm c}^2}{\pi r_0^2}=Nd(\pi \rho_c^2 ) }[/math]

where [math]\displaystyle{ \pi r_0^2=\frac{1}{Nd} }[/math] is the occupied area by each row of atoms having an average distance d in a material, with a density N (expressed as atoms / cm ^ 3). Therefore, [math]\displaystyle{ \chi_{\rm min} }[/math] is an estimation of the smallest fraction of de-channeled ions that can be obtained from a material perfectly aligned to the ion beam. By considering a single crystal of silicon, oriented along the <110>, a [math]\displaystyle{ \chi_{\rm min}=1.35 ~ 10^{-2} }[/math] can be calculated, in good agreement with the experimental values.

Further considerations can be made by considering the thermal vibration motion of the nuclei: for this discussion, see the reference.^[11]

The critical angle [math]\displaystyle{ \psi_{\rm c} }[/math] can be defined as the angle such that if the ion enters with an angle smaller than the critical angle it will be channeled vice versa its transverse energy will allow it to escape to the periodic potential.

[math]\displaystyle{ \psi_{\rm c}=\sqrt{\frac{U(r_{\rm min})}{E}} }[/math]

Using the Lindhard potential and assuming the amplitude of thermal vibration [math]\displaystyle{ \rho }[/math] as the minimum approach distance.

[math]\displaystyle{ \psi_{\rm c}(\rho)=\sqrt{\frac{Z_1Z_2e^2}{Ed} }\left[\ln \left(\frac{C_a}{\rho} \right)^2 +1 \right]^{1/2} }[/math]

Typical critical angles values (at room temperature) are for silicon <110> 0.71 °, for germanium <100> 0.89 °, for tungsten <100> 2.17 °.

Similar consideration can be made for planar channelling. In this case, the average of the atomic potentials will cause the ions to be confined between charge planes that correspond to a continuous planar potential [math]\displaystyle{ U_{\rm p}(\rho) }[/math].

[math]\displaystyle{ U_{\rm p}(y)=Nd_{\rm p} \int V \left (\sqrt{y^2+r^2}\right ) ~2\pi r~\mathrm{d}r = 2\pi Z_1Z_2e^2aNd_{\rm p}\left( \sqrt{\left( \frac{y}{a}\right)^2 +C^2}- \frac{y}{a} \right) }[/math]

where [math]\displaystyle{ Nd_{\rm p} }[/math] are the average number of atoms per unit area in the plane, [math]\displaystyle{ d_{\rm p} }[/math] is the spacing between crystallographic planes and y is the distance from the plane. Planar channelling has critical angles that are a factor of 2-4 smaller than axial analogs and a [math]\displaystyle{ \chi_{\rm min} }[/math] which is greater than axial channelling, with values that are around 10-20%, comparing with > 99% of axial channelling. A complete discussion of planar channelling can be found in references.^[11][12]

5. General Literature

• J.W. Mayer and E. Rimini, Ion Beam Handbook for Material Analysis, (1977) Academic Press, New York
• L.C. Feldman, J.W. Mayer and S.T.Picraux, Material Analysis by Ion Channelling, (1982) Academic Press, New York
• R. Hovden, H. L. Xin, D. A. Muller, Phys. Rev. B 86, 195415 (2012) arXiv:1212.1154
• G. R. Anstis, D. Q. Cai, and D. J. H. Cockayne, Ultramicroscopy 94, 309 (2003).
• D. Van Dyck and J. H. Chen, Solid State Communications 109, 501 (1999).
• S. Hillyard and J. Silcox, Ultramicroscopy 58, 6 (1995).
• S. J. Pennycook and D. E. Jesson, Physical Review Letters 64, 938 (1990).
• M. V. Berry and Ozoriode.Am, Journal of Physics a-Mathematical and General 6, 1451 (1973).
• M. V. Berry, Journal of Physics Part C Solid State Physics 4, 697 (1971).
• A. Howie, Philosophical Magazine 14, 223 (1966).
• P. B. Hirsch, A. Howie, R. B. Nicholson, D. W. Pashley, and M. Whelan, Electron microscopy of thin crystals (Butterworths London, 1965).
• J. U. Andersen, Notes on Channeling, http://phys.au.dk/en/publications/lecture-notes/ (2014)

The content is sourced from: https://handwiki.org/wiki/Physics:Channelling