Base isolation techniques have emerged as the most effective seismic damage mitigation strategies. Several types of aseismic devices for base isolation have been invented, studied, and used. Out of several isolation systems, sliding isolation systems are popular due to their operational simplicity and ease of manufacturing. These isolators behave passively i.e. their properties of independent of frequency of earthquake excitation. Herein, the historical development of passive sliding isolators based on the number of sliding surfaces is discussed.
- base isolation
- friction pendulum system
- multi-surface isolation system
- passive isolation system
1. Introduction
Earthquakes are one of the most catastrophic natural events, often resulting in the loss of lives and structures. Humans have been trying to reduce the harmful effects of earthquakes on structures, such as buildings, bridges, and tanks. The main challenge faced in reducing the harmful effect of an earthquake is to arrive at a suitable method to dissipate or offset the vast amount of energy imparted to the structure during a seismic event. In this regard, researchers have been developing some mechanical appurtenances over the years. As a result, several mechanical devices, such as fluid viscous dampers [1], visco-elastic dampers [2] , and yielding-type dampers [3], have been invented. Depending on their location and type of arrangement within the structure, these devices absorb seismic energy locally. Over the years, the research focus shifted to developing mechanical devices that can significantly reduce the transfer of seismic energy to the structure, which led to the invention of base isolation systems. In principle, a base isolation system must have very high stiffness in the vertical direction and low stiffness in the lateral direction. High vertical stiffness enables the transfer of gravity loads, whereas low lateral stiffness ensures that the structure behaves as a rigid unit for the lateral load. The main issue to be addressed in the earthquake-resistant design of structures is the resonance problem. During a seismic event, structures generally are prone to frequency amplification as their fundamental frequency typically lies in the range of earthquake frequencies. Base isolation systems minimize the resonance issue by significantly altering the fundamental frequency of the structure.
One of the simplest ways to achieve base isolation is to implement some sliding mechanism between the superstructure and substructure. In its simplest form, this type of isolation can use a sand layer between the superstructure and substructures [4]. Although this approach is simple and reasonably effective for small structures, it is not suitable for multi-story buildings. More recently, Azinović et al. [5] proposed the use of thermal insulation boards installed beneath the foundations of a contemporary energy-efficient building to allow for controlled lateral sliding between the individual layers of the board. Out of the various scenarios considered by these researchers, the sliding prevention scenario was found to be the most cost-effective. To date, several varieties of sliding isolation systems have been developed. These systems are discussed in detail in the subsequent sections. Although the idea of seismic isolation is more than a century old, research and wide practical implementation started about 40 years ago. Since its inception, the concept of base isolation has significantly matured, and various base isolators have been developed, patented, and implemented.
2. Sliding Isolation Systems with a Single Sliding Surface
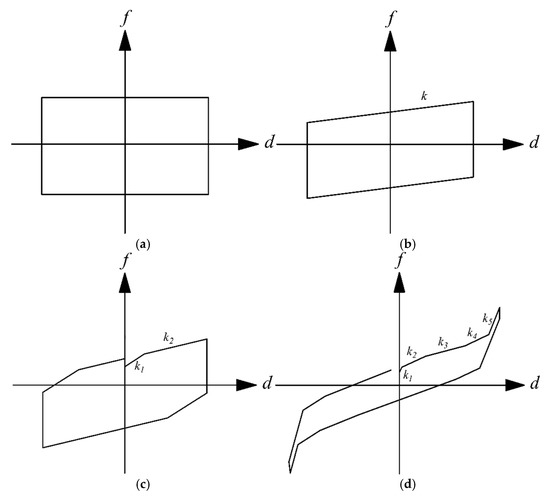
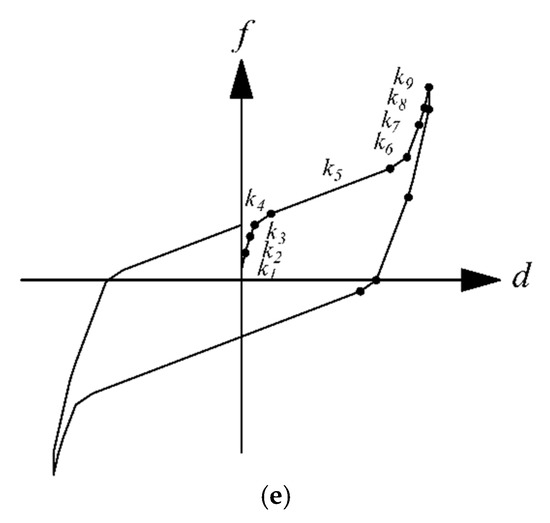
3. Sliding Isolation Systems with Multiple Sliding Surfaces
This entry is adapted from the peer-reviewed paper 10.3390/buildings12111997
References
- Symans, M.D.; Constantinou, M.; Passive Fluid Viscous Damping Systems for Seismic Energy Dissipation. J. Earthq. Technol. 1998, 35, 185-206, .
- Chang, K.C.; Soong T.T.; Oh, S.-T.; Lai, M.L.; Seismic Behavior of Steel Frame with Added Viscoelastic Dampers. J. Struct. Eng. 1995, 121, 1418–1426, https://doi.org/10.1061/(ASCE)0733-9445(1995)121:10(1418).
- Skinner, R.I.; Kelly, J.M.; Heine, A.J.; Hysteretic Dampers for Earthquake-Resistant Structures. Earthq. Eng. Struct. 1974, 3, 287–296, https://doi.org/10.1002/eqe.4290030307.
- Li, L. Base Isolation Measure for Aseismic Buildings in China. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984; Volume 6, pp. 791–798.
- Azinovi´c, B.; Kilar, V.; Koren, D.; Energy-Efficient Solution for the Foundation of Passive Houses in Earthquake-Prone Regions.. Eng. Struct. 2016, 112, 133–145., https://doi.org/10.1016/j.engstruct.2016.01.015.
- Qamaruddin, M. Development of Brick Building Systems for Improved Earthquake Performance. Ph.D. Thesis, University of Roorkee, Roorkee, India, 1978.
- Arya, A.S.; Chandra, B.; Qamaruddin, M. A New Building System for Improved Earthquake Performance. In Proceedings of the Sixth Symposium on Earthquake Engineering, IIT Roorkee (Formerly, University of Roorkee), Roorkee, India, 5–7 October 1978; Volume 1, pp. 499–504.
- Arya, A.S.; Qamaruddin, M.; Chandra, B. New System of Brick Buildings for Improved Behaviour during Earthquakes. In Proceedings of the Seventh World Conference on Earthquake Engineering, Istanbul, Turkey, 8–13 September 1980; pp. 225–232.
- Mostaghel, N.; Hejazi, M.; Tanbakuchi, J. Response of Sliding Structures to Harmonic Support Motion. Earthq. Eng. Struct. Dyn. 1983, 11, 355–366.
- Westermo, B.; Udwadia, F. Periodic Response of a Sliding Oscillator System to Harmonic Excitation. Earthq. Eng. Struct. Dyn. 1983, 11, 135–146.
- Nikolić-Brzev, S. An Innovative Seismic Protection Scheme for Masonry Buildings. In Proceedings of the 10th International Conference on Brick/Block Masonry, Calgary, AB, Canada, 5–7 July 1994; pp. 273–282.
- Mostaghel, N.; Tanbakuchi, J. Response of Sliding Structures to Earthquake Support Motion. Earthq. Eng. Struct. Dyn. 1983, 11, 729–748.
- Yang, Y.-B.; Lee, T.-Y.; Tsai, I.-C. Response of Multi-Degree-of-Freedom Structures with Sliding Supports. Earthq. Eng. Struct. Dyn. 1990, 19, 739–752.
- Vafai, A.; Hamidi, M.; Ahmadi, G. Numerical Modeling of MDOF Structures with Sliding Supports Using Rigid-Plastic Link. Earthq. Eng. Struct. Dyn. 2001, 30, 27–42.
- Krishnamoorthy, A.; Saumil, P. In-Plane Response of a Symmetric Space Frame with Sliding Upports. Int. J. Appl. Sci. Eng. 2005, 3, 1–11.
- Krishnamoorthy, A. An Absolute Displacement Approach for Modeling of Sliding Structures. Struct. Eng. Mech. 2008, 29, 659–671.
- Zayas, V.A.; Low, S.S.; Mahin, S.A. A Simple Pendulum Technique for Achieving Seismic Isolation. Earthq. Spectra 1990, 6, 317–333.
- Mokha, A.; Constantinou, M.C.; Reinhorn, A.M.; Zayas, V.A. Experimental Study of Friction-pendulum Isolation System. J. Struct. Eng. 1991, 117, 1201–1217.
- Gilberto, M.; Whittaker, A.S.; Fenves, G.L.; Mahin, S.A. Experimental and Analytical Studies of the Friction Pendulum System for the Seismic Protection of Simple Bridges; Earthquake Engineering Research Center: Berkeley, CA, USA, 2004; p. 110.
- Jangid, R.S. Optimum Friction Pendulum System for Near-Fault Motions. Eng. Struct. 2005, 27, 349–359.
- Castaldo, P.; Amendola, G. Optimal Sliding Friction Coefficients for Isolated Viaducts and Bridges: A Comparison Study. Struct. Contr. Health Monit. 2021, 28, e2838.
- Vibhute, A.S.; Bharati, S.D.; Shrimali, M.K.; Datta, T.K. Optimum Coefficient of Friction in FPS for Base Isolation of Building Frames. Pract. Period. Struct. Des. Constr. 2022, 27, 04022042.
- Tsai, C.S. Finite Element Formulations for Friction Pendulum Seismic Isolation Bearings. Int. J. Numer. Methods Eng. 1997, 40, 29–49.
- Ryan, K.L.; Chopra, A.K. Estimating the Seismic Displacement of Friction Pendulum Isolators Based on Non-Linear Response History Analysis. Earthq. Eng. Struct. Dyn. 2004, 33, 359–373.
- Mazza, F.; Sisinno, S. Nonlinear Dynamic Behavior of Base-Isolated Buildings with the Friction Pendulum System Subjected to near-Fault Earthquakes. Mech. Based Des. Struct. Mach. 2017, 45, 331–344.
- Wang, Y.-P.; Chung, L.-L.; Liao, W.-H. Seismic Response Analysis of Bridges Isolated with Friction Pendulum Bearings. Earthq. Eng. Struct. Dyn. 1998, 27, 1069–1093.
- Seleemah, A.A.; El-Sharkawy, M. Seismic Response of Base Isolated Liquid Storage Ground Tanks. Ain Shams Eng. J. 2011, 2, 33–42.
- Whittaker, A.S.; Kumar, M.; Kumar, M. Seismic Isolation of Nuclear Power Plants. Nucl. Eng. Technol. 2014, 46, 569–580.
- Almazán, J.L.; De La Llera, J.C.; Inaudi, J.A. Modelling Aspects of Structures Isolated with the Frictional Pendulum System. Earthq. Eng. Struct. Dyn. 1998, 27, 845–867.
- Monti, G.; Petrone, F. Analytical Thermo-Mechanics 3D Model of Friction Pendulum Bearings. Earthq. Eng. Struct. Dyn. 2016, 45, 957–977.
- Oliveto, N.D. Geometrically Nonlinear Analysis of Friction Pendulum Systems under Tri-Directional Excitation. Eng. Struct. 2022, 269, 114770.
- Hall, J.F.; Heaton, T.H.; Halling, M.W.; Wald, D.J. Near-Source Ground Motion and Its Effects on Flexible Buildings. Earthq. Spectra 1995, 11, 569–605.
- Pranesh, M.; Sinha, R. VFPI: An Isolation Device for Aseismic Design. Earthq. Eng. Struct. Dyn. 2000, 29, 603–627.
- Tsai, C.S.; Chiang, T.-C.; Chen, B.-J. Finite Element Formulations and Theoretical Study for Variable Curvature Friction Pendulum System. Eng. Struct. 2003, 25, 1719–1730.
- Lu, L.-Y.; Shih, M.-H.; Wu, C.-Y. Near-Fault Seismic Isolation Using Sliding Bearings with Variable Curvatures. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004.
- Malu, G.; Pranesh, M. Sliding Isolation Systems: State-of-the-Art Review. IOSR J. Civ. Eng. 2013, 6, 30–35.
- Lu, L.-Y.; Wang, J.; Hsu, C.-C. Sliding Isolation Variable Frequency Bearings for near—Fault Ground Motions. In Proceedings of the 4th International Conference on Earthquake Engineering, Taipei, Taiwan, 12–13 October 2006.
- Krishnamoorthy, A. Seismic Isolation of Bridges Using Variable Frequency and Variable Friction Pendulum Isolator System. Struct. Eng. Int. 2010, 20, 178–184.
- Malu, G.; Murnal, P. Variable Coefficient of Friction: An Effective VFPI Parameter to Control near-Fault Ground Motions. ISET J. Earthq. Technol. 2012, 49, 73–87.
- Calvi, P.M.; Moratti, M.; Calvi, G.M. Seismic Isolation Devices Based on Sliding between Surfaces with Variable Friction Coefficient. Earthq. Spectra 2016, 32, 2291–2315.
- Brito, M.B.; Ishibashi, H.; Akiyama, M. Shaking Table Tests of a Reinforced Concrete Bridge Pier with a Low-cost Sliding Pendulum System. Earthq. Eng. Struct. Dyn. 2019, 48, 366–386.
- Touaillon, J. Improvement in Buildings. US Patent No. 99. 973, 1870.
- Tsai, C.S.; Chiang, T.-C.; Chen, B.-J. Experimental Study for Multiple Friction Pendulum System. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004.
- Fenz, D.M.; Constantinou, M.C. Behaviour of the Double Concave Friction Pendulum Bearing. Earthq. Eng. Struct. Dyn. 2006, 35, 1403–1424.
- Fenz, D.M.; Constantinou, M.C. Modeling Triple Friction Pendulum Bearings for Response-History Analysis. Earthq. Spectra 2008, 24, 1011–1028.
- Fenz, D.M.; Constantinou, M.C. Spherical Sliding Isolation Bearings with Adaptive Behavior: Theory. Earthq. Eng. Struct. Dyn. 2008, 37, 163–183.
- Fenz, D.M.; Constantinou, M.C. Spherical Sliding Isolation Bearings with Adaptive Behavior: Experimental Verification. Earthq. Eng. Struct. Dyn. 2008, 37, 185–205.
- Becker, T.C.; Mahin, S.A. Experimental and Analytical Study of the Bi-Directional Behavior of the Triple Friction Pendulum Isolator. Earthq. Eng. Struct. Dyn. 2012, 41, 355–373.
- Sarlis, A.A.; Constantinou, M.C. A Model of Triple Friction Pendulum Bearing for General Geometric and Frictional Parameters: Revised Triple Friction Pendulum Bearing Model. Earthq. Eng. Struct. Dyn. 2016, 45, 1837–1853.
- Morgan, T.A.; Mahin, S.A. Achieving Reliable Seismic Performance Enhancement Using Multi-Stage Friction Pendulum Isolators. Earthq. Eng. Struct. Dyn. 2010, 39, 1443–1461.
- Becker, T.C.; Bao, Y.; Mahin, S.A. Extreme Behavior in a Triple Friction Pendulum Isolated Frame. Earthq. Eng. Struct. Dyn. 2017, 46, 2683–2698.
- Lee, D.; Constantinou, M.C. Quintuple Friction Pendulum Isolator: Behavior, Modeling, and Validation. Earthq. Spectra 2016, 32, 1607–1626.
- Keikha, H.; Amiri, G.G. Seismic Performance Assessment of Quintuple Friction Pendulum Isolator with a Focus on Frictional Behavior Impressionability from Velocity and Temperature. J. Earthq. Eng. 2019, 25, 1256–1286.
- Sodha, A.; Vasanwala, S.A.; Soni, D. Probabilistic Evaluation of Seismically Isolated Building Using Quintuple Friction Pendulum Isolator. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; pp. 149–159. ISBN 9789811319655.
- Marin-Artieda Claudia, C.; Whittaker Andrew, S.; Theoretical Studies of the XY-FP Seismic Isolation Bearing for Bridges. J. Bridge Eng. 2010, 15, 631-638, https://doi.org/10.1061/(ASCE)BE.1943-5592.0000103.
- Yang, C.-Y.; Wang, S.-J.; Lin, C.-K.; Chung, L.-L.; Liou, M.-C.; Analytical and Experimental Study on Sloped Sliding-Type Bearings. Struct. Control Health Monit. 2021, 28, e2828, https://doi.org/10.1002/stc.2828.
