A quantum-classical system is a system consisting of two interacting subsystems, one of which behaves classically, and the other requires a quantum description.
- quantum-classical system
- Liouville equation
- Heisenberg equation
- von Neumann equation
1. Introduction
Quantum-classical systems are systems consisting of two interacting subsystems, one of which behaves classically, and the other requires a quantum description [1][2][3][4]. Over the past decade, the mathematical formularization of quantum-classical dynamics has attracted considerable interest [5][6][7][8], and, as it turned out, there are conceptual difficulties in this problem.
Quantum-classical systems are described in terms of two objects: observables and states. The functional mean value of observables determines a duality between observables and states, and, as a result, there are two equivalent approaches to describing evolution, namely within the framework of the evolution of observables or the evolution of states.
2. Formula Derivation
The observable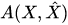 of a quantum-classical system is a function of canonical variables
of a quantum-classical system is a function of canonical variables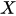 characterizing classical degrees of freedom, and of non-commuting self-adjoint operators
characterizing classical degrees of freedom, and of non-commuting self-adjoint operators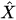 satisfying canonical commutation relations, characterizing quantum degrees of freedom. For example, the Hamiltonian of a quantum-classical system has the following structure:
satisfying canonical commutation relations, characterizing quantum degrees of freedom. For example, the Hamiltonian of a quantum-classical system has the following structure: 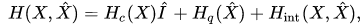 where
where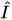 is a unit operator,
is a unit operator, 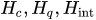 are the Hamiltonians of classical and of quantum degrees of freedom and their interactions, respectively.
are the Hamiltonians of classical and of quantum degrees of freedom and their interactions, respectively.
Further, as an example, we consider a one-dimensional system consisting of a classical particle and a quantum one with unit masses. In this case
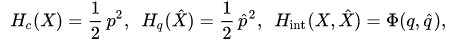
where 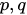 are canonical variables of a classical particle,
are canonical variables of a classical particle, 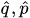 are self-adjoint operators satisfying canonical commutation relations and the function
are self-adjoint operators satisfying canonical commutation relations and the function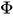 is an interaction potential.
is an interaction potential.
The mean value of the observable 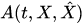 at an instant
at an instant 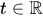 (expectation value) is determined by the positive continuous linear functional on the space of observables, which has the following two representations:
(expectation value) is determined by the positive continuous linear functional on the space of observables, which has the following two representations:
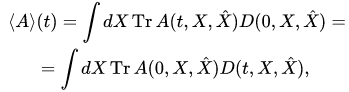 (1)
(1)
where 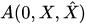 is an observable at the initial instant, the state of a quantum-classical system is described by so-called the density operator
is an observable at the initial instant, the state of a quantum-classical system is described by so-called the density operator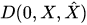 , which depends on classical canonical variables (its kernel is a density matrix depending on classical canonical variables), such that
, which depends on classical canonical variables (its kernel is a density matrix depending on classical canonical variables), such that 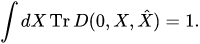
The evolution of observables of a quantum-classical system is described by the following initial-value problem:
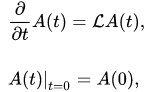 (2)
(2)
where the generator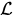 of this evolution equation depends on the quantization rule of a quantum subsystem. In the case of the Weyl quantization rule it has the form
of this evolution equation depends on the quantization rule of a quantum subsystem. In the case of the Weyl quantization rule it has the form
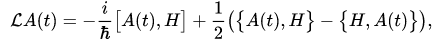 (3)
(3)
where 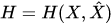 is the Hamiltonian,
is the Hamiltonian, 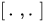 is a commutator of operators, and
is a commutator of operators, and 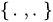 is the Poisson bracket. For some other quantization rules, the operator
is the Poisson bracket. For some other quantization rules, the operator 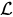 is defined in [1][2][4].
is defined in [1][2][4].
In the case of a one-dimensional system consisting of classical and quantum particles in the configuration space representation, generator (3) has the form
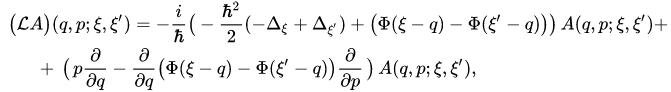
where 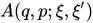 is a kernel of the operator-valued function
is a kernel of the operator-valued function 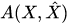 in the configuration space representation, and in the Wigner representation it looks as follows
in the configuration space representation, and in the Wigner representation it looks as follows
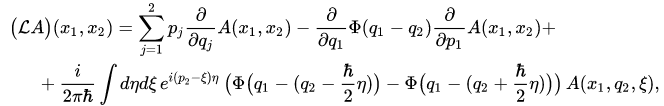
where 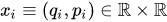 and
and 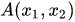 is a symbol of the operator-valued function
is a symbol of the operator-valued function 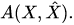
Usually, the evolution of a quantum-classical system is described within the framework of the evolution of states [2][4], namely by the evolution equation dual to equation (2)
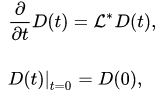 (4)
(4)
where the generator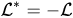 is an operator adjoint to the operator (3) in the sense of functional (1).
is an operator adjoint to the operator (3) in the sense of functional (1).
Hereafter we consider the self-consistent field approximation of this equation [G(1981)]. For that we introduce the marginal states of classical and quantum subsystems:
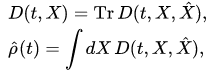 (5),(6)
(5),(6)
respectively, and the correlation of the classical and quantum subsystems
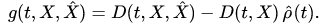 (7)
(7)
If we assume that at any instant of time there are no correlations between classical and quantum subsystems, i.e. it is true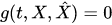 , then in such approximation, we derive from equation (4) the self-consistent equations set of the Liouville and von Neumann equations for marginal states (5),(6) of the classical and quantum subsystems
, then in such approximation, we derive from equation (4) the self-consistent equations set of the Liouville and von Neumann equations for marginal states (5),(6) of the classical and quantum subsystems
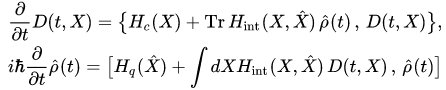 (8),(9)
(8),(9)
with the corresponding initial states
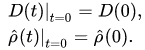
We note that the initial-value problem for equations (8),(9) describes the evolution of all possible states of quantum-classical systems in the absence of correlations between the classical and quantum subsystems(the self-consistent field approximation). This type of approximation can not be treated as the mean-field approximation since we consider systems of finitely many particles while the mean-field approximation assumes the transition to the thermodynamic limit, i.e. it has a sense for systems of infinitely many particles.
If at the initial moment the states of the classical and quantum subsystems are pure states, i.e.
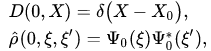 (10)
(10)
where 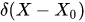 is the Dirac measure,
is the Dirac measure,  is the phase space point in which we measure observables of a classical subsystem,
is the phase space point in which we measure observables of a classical subsystem, 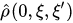 is a kernel (a density matrix) of marginal density operator (6) in the configuration space representation (it is a rank one projection on the vector
is a kernel (a density matrix) of marginal density operator (6) in the configuration space representation (it is a rank one projection on the vector 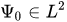 ), then in the configuration space representation
), then in the configuration space representation
the initial-value problem for equations (8),(9) is equivalent to the initial-value problem for a self-consistent set of equations of Hamilton and Schrödinger:
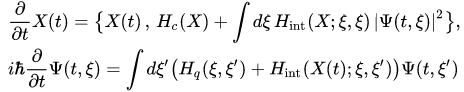 (11),(12)
(11),(12)
with initial data
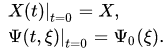
For example, in the case of a one-dimensional system consisting of classical and quantum particles, the equations (11),(12) take the form
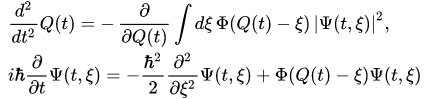
with initial data (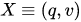 )
)
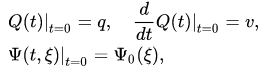
where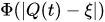 is a two-body interaction potential,
is a two-body interaction potential, 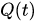 is a position at the instant
is a position at the instant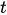 of a classical particle in the space. Such a self-consistent set of equations of Newton and Schrödinger is usually used for the description of the evolution of states of quantum-classical systems.
of a classical particle in the space. Such a self-consistent set of equations of Newton and Schrödinger is usually used for the description of the evolution of states of quantum-classical systems.
Now we consider the description of a quantum-classical system in the self-consistent field approximation (7) between the classical and quantum particles by means of the evolution of observables.
We assume that the initial state of a quantum-classical system specified by the initial uncorrelation pure state (10), i.e.
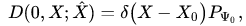 (13)
(13)
where 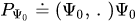 (or in the Dirac notation:
(or in the Dirac notation: 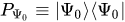 ) is a one-dimensional projector onto a unit vector ${\Psi_0}$ from a Hilbert space. In the configuration space representation, a kernel of operator-valued function (13) has the form
) is a one-dimensional projector onto a unit vector ${\Psi_0}$ from a Hilbert space. In the configuration space representation, a kernel of operator-valued function (13) has the form
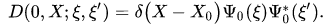
We emphasize that the problem of how to define a pure state of the quantum-classical system is an open problem.
Then according to equality (1), in this approximation the evolution of the canonical observables of quantum and classical particles is described by the following set of equations:
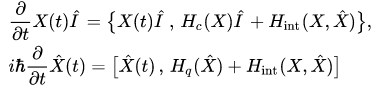 (14),(15)
(14),(15)
with the corresponding initial data
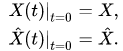
For example, in the case of a one-dimensional system, consisting of the classical and quantum particles, equations (14),(15) could be rewritten for pairs of canonically conjugated variables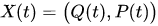 and
and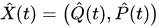 as follows
as follows
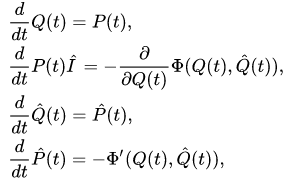
where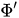 is the derivative of the function
is the derivative of the function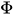 . These equations can also be rewritten similar to (11),(12) as equations in the configuration space representation. In the Wigner representation, they take the following fascinating form
. These equations can also be rewritten similar to (11),(12) as equations in the configuration space representation. In the Wigner representation, they take the following fascinating form
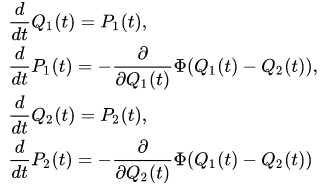
with initial data
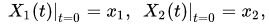
where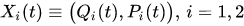 , and
, and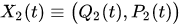 are symbols of the operators
are symbols of the operators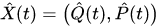 . We note that in this representation a symbol of the uncorrelation pure state (13) is determined by the following Wigner function
. We note that in this representation a symbol of the uncorrelation pure state (13) is determined by the following Wigner function
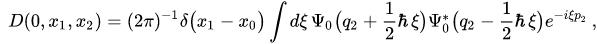
and the mean value of the observable is determined by the following functional
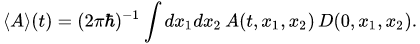
Thus, quantum-classical dynamics is governed by the quantum-classical equation (2) within the framework of the evolution of observables or by the quantum-classical equation (4) within the framework of the evolution of states. A quantum-classical system can be described by the self-consistent Hamilton and Schr\"{o}dinger equations set (11),(12) as well as by means of the self-consistent set of equations of Hamilton (14) and Heisenberg (15) in the case of uncorrelation states.
References
- Gerasimenko V. I.; Quantum-classical systems. The evolution of finite systems. Preprint 80-92P, Kyiv: Inst. Theor. Phys. 1980, 92P, 20, .
- V. I. Gerasimenko; Correlationless equations of motion of quantum-classical systems. Reports of Acad. Sci. Ukrainian SSR 1981, 10, 65-68, .
- I. V. Aleksandrov; The Statistical Dynamics of a System Consisting of a Classical and a Quantum Subsystem . Z. Naturforsch. 1981, 36a, 902-908, .
- Viktor Gerasimenko; Dynamical equations of quantum-classical systems. Theoretical and Mathematical Physics 1982, 50, 49-55, 10.1007/bf01027604.
- Denys I. Bondar; François Gay-Balmaz; Cesare Tronci; Koopman wavefunctions and classical–quantum correlation dynamics. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2019, 475, 20180879, 10.1098/rspa.2018.0879.
- François Gay-Balmaz; Cesare Tronci; Madelung transform and probability densities in hybrid quantum–classical dynamics. Nonlinearity 2020, 33, 5383-5424, 10.1088/1361-6544/aba233.
- Raymond Kapral; PROGRESS IN THE THEORY OF MIXED QUANTUM-CLASSICAL DYNAMICS. Annual Review of Physical Chemistry 2006, 57, 129-157, 10.1146/annurev.physchem.57.032905.104702.
- G. Ciccotti, D. Coker, R. Kapral. Quantum Dynamics of Complex Molecular Systems; David A. MichaIrene Burghardt, Eds.; Springer: Berlin, 2007; pp. 275-293.
