Particle Swarm Optimization in Residential Demand-Side Management: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Christoforos Menos-Aikateriniadis
,
Ilias Lamprinos
,
Pavlos S. Georgilakis

Power networks at the distribution level are becoming more complex in their behavior and more heavily stressed due to the growth of decentralized energy sources. Demand response (DR) programs can increase the level of flexibility on the demand side by discriminating the consumption patterns of end-users from their typical profiles in response to market signals. The exploitation of artificial intelligence (AI) methods in demand response applications has attracted increasing interest in recent years. Particle swarm optimization (PSO) is a computational intelligence (CI) method that belongs to the field of AI and is widely used for resources scheduling, mainly due to its relatively low complexity and computational requirements and its ability to identify near-optimal solutions in a reasonable timeframe.

  • artificial intelligence
  • computational intelligence
  • particle swarm optimization
  • demand-side management
  • demand response
  • distributed energy resources
  • smart grid
  • electric vehicles
  • energy storage
  • resource scheduling
  • load control

1. Introduction

The rapidly increasing integration of decentralized energy resources, such as solar photovoltaic (PV) systems, energy storage, and electric vehicles (EVs), along with the use of power-electronic-interfaced loads, such as heat pumps, have increased the complexity of low-voltage (LV) grids. This new set of appliances and domestic loads can distort consumer habits and thus impact typical consumption patterns. Therefore, the balance between intermittent generation in almost real time and unpredictable demand, voltage control, frequency regulation, and power quality monitoring have become more and more crucial for maintaining power system stability and reliability. Traditionally, this burden would fall under the responsibility of power system operators, who in turn should reinforce the grid to tackle these challenges. However, in the smart grid era, power flows are bidirectional, and consumers can actively contribute towards a more reliable, efficient, and flexible power grid. One of the most promising solutions at the distribution level is demand-side management (DSM). Reducing peak electricity demand, shifting the load from peak to off-peak hours, and decreasing/increasing hourly electricity consumption are some of the benefits that DSM can provide [1].
DSM actions can be implemented through demand response (DR) programs. Currently, DR programs can be classified into either price-based or incentive-based [2][3][4]. In the former, customers can modify their electricity consumption based on the electricity tariff applied. A time-of-use (ToU) tariff is the most common price-based DR program, where a fixed set of electricity prices can vary within the hours of the day (e.g., day vs. night tariff) and the days of the week (e.g., weekdays vs. weekend). Other programs include critical peak pricing (higher tariffs applied during peak demand hours) and real-time pricing (tariffs change dynamically within the day, usually on an hourly basis). Incentive-based programs can be further split into voluntary, mandatory, and market-clearing programs [4]. The most popular voluntary scheme in residential and commercial applications is direct load control (DLC), where special incentives (bill credits, discounts, or rewards) are offered to end-users so that they shift their demand during the day. In that case, consumers voluntarily participate either directly, by turning on/off their loads, or indirectly, by collaborating with a third-party (e.g., aggregator) who is responsible for automatically and remotely controlling consumer assets to provide the requested services. Mandatory DR schemes are more applicable to large industrial consumers. During critical hours, when the power network is under stress, industrial consumers might be instructed by system operators to reduce their consumption (load curtailment). Market-clearing programs offer the opportunity to large consumers (industrial or aggregated) to bid and participate in the wholesale electricity market when flexibility products, such as demand reduction, are needed.
This work is focused on residential demand response applications that have attracted increasing interest in the literature in recent years. Using data gathered from smart meters installed at each customer’s point of connection, consumers can keep track of their appliances’ consumption and subsequently change their behavior directly or while collaborating with a third-party service provider. The main benefits of residential demand response applications are [5][6]:

Economic benefits:

  • DR can lead to dispatching fewer hours of uneconomical generation units when the power system becomes tight, i.e., when generation cannot meet demand or when the security of supply margins decreases;
  • End-users profit by either consuming in low-tariff hours, selling power back to the grid with the use of local storage, or other incentives (e.g., bill discount);
  • DR can decrease distribution network stress and therefore reduce the need for network investments.
  • Power system operation:
  • System reliability increases when providing frequency response, contingency reserves, and flexibility services;
  • Renewable energy source (RES) curtailment is reduced by modifying demand to match green power generation.

Reduction in greenhouse gas emissions:

  • Utilization of distributed resources (EVs, PVs, and local storage) is higher;
  • Energy efficiency is higher, and thus, energy consumption decreases.
Recent research has shown that computational intelligence (CI) and machine learning (ML) methods can be computationally faster and more accurate than physical models (white-box methods) and statistical methods in numerous residential demand response applications [7][8]. For instance, when predicting energy consumption in buildings with white-box methods, the physical properties of the energy systems need to be modeled using a detailed set of input parameters [7]. These parameters are often hard to retrieve, the mathematical formulation behind the optimization can be quite complex, and the model outputs are highly case-dependent. In black-box models, there is little need for understanding the physical mechanisms of the energy systems. However, there is a requirement for a large set of historical data to train the models. Gray-box methods constitute a combination of the above, where a rather small historical dataset is used to train statistical models that are based on a high-level knowledge of the physical energy systems. Advantages over black-box methods are the need for less data for training the statistical models and the better explainability of the modeling process and results since they are interpreted in physical terms. However, these models are customized to specific applications, such as modeling individual components in residential HVAC systems [9], and cannot easily generalize over a diverse group of energy systems. Additionally, there is still a need to retrieve the physical parameters of the energy systems, and this can increase the complexity in specific applications.
For the above reasons, several AI algorithms, such as reinforcement learning (RL), evolutionary algorithms, swarm AI, and artificial neural networks (ANN), have been suggested for the control, optimization, and scheduling of distributed energy systems. Furthermore, methods that are model-free and highly adaptable, such as particle swarm optimization (PSO), have been recommended when addressing the need for the maximization of end-user comfort along with the minimization of energy consumption and costs [7][10]. Combining these criteria in residential demand response management systems could make DR more appealing to consumers and, thus, increase its applicability in households and commercial buildings.
To date, there have been a few review papers in the area of AI for residential demand response applications. The review in [11] examines the use of reinforcement learning (RL) for demand response applications in buildings covering a wide range of energy systems, such as distributed generation, storage, and HVAC. The applicability of RL to scheduling and control of residential loads was studied, taking into consideration user comfort and satisfaction. However, other methods, such as ANN, swarm AI, and evolutionary algorithms, have also been used in research to solve load scheduling and control from the consumer side, as shown in [10]. On the other hand, [12] provides a more holistic view of the use of deep reinforcement learning in power systems without specifically focusing on demand response applications. The review in [7] focuses on air-conditioning system control strategies, optimization techniques, and thermal modeling (white-, black-, and gray-box methods). Similarly, [8] provides the first survey of ML methods for electric water heater (EWH) optimization and scheduling. Another review that focuses on a specific energy system is [13], which reviews techniques for HVAC system control and optimization. An interesting review is [14], where the AI methods analyzed consider both thermal comfort and energy savings. However, the limitation of [14] is that it investigates only thermal energy systems for residential demand response. In [15], the classification of AI methods was based on the optimization objective (energy, comfort, safety, design, and maintenance). The aforementioned analysis revealed that AI methods in demand response applications are a growing research area with room for further investigation since every author categorizes them differently.

2. Models for Residential Load Scheduling and Control Using PSO

Scheduling and control of decentralized energy resources, in practice, is a stochastic mathematical problem, given the intermittency of renewable generation, the uncertainty of users’ consumption patterns, and continuously changing electricity prices, which, in most of the reviewed works, is a key driver. Additionally, the large number and diversity of household appliances and the consideration of user thermal comfort and convenience increase the complexity of optimization, where classical computational techniques such as linear programming (LP), integer linear programming (ILP), and mixed-integer linear programming (MILP) cannot provide feasible solutions within a reasonable timeframe [16]. On the contrary, heuristic optimization techniques, such as PSO, genetic algorithms (GA), ant colony optimization (ACO), and wind-driven optimization (WDO), can support more complex optimization problems with the identification of near-optimal solutions.
In this work, PSO-based resource scheduling models are reviewed given the research “gap” identified in Section 1 but also due to the fact that it presents the following advantages over similar nature-inspired optimization techniques [10][16][17][18][19]:
  • It requires fewer parameters for tuning and adjustment;
  • Easier implementation and less computational effort are usually needed to reach a near-optimal solution compared to other heuristic algorithms;
  • The histories of all particles contribute to the search, while in other methods (e.g., GA), the algorithm’s memory capability is lower due to the replacement of the old population with a new, more efficient one.
In the reviewed research works [16][19][20][21][22][23][24][25][26][27][28][29][30][31][32][33][34][35][36][37][38][39][40][41][42][43][44][45][46][47][48][49][50][51][52][53][54][55][56][57][58][59][60][61][62][63][64] [65][66][67][68][69][70][71][72][73][74][75][76][77][78][79][80][81], different models were designed. They can be classified based on the optimization objectives, the system constraints applied, or the energy system applications. In the latter, the type of energy resources (EVs, distributed generation, energy storage, or appliance type), the number of users (single or multiple), and the type of control (local, decentralized, or centralized) are included.

2.1. Optimization Objectives

One of the main considerations of scheduling and control for demand-side management is the formulation of the objective function that needs to be optimized. Additionally, it is very important to define the system constraints and operational limits of key variables that will collectively shape the boundaries of the optimization search space. Optimization objectives can be categorized into the following three groups based on the number of objectives that are investigated.
Single objective:
 In the majority of the reviewed works, the main objective was to optimally schedule different energy resources in order to minimize electricity costs, with or without taking into consideration user comfort, convenience, and peak-to-average (PAR) ratio. Depending on the complexity of the problem, the cost minimization function consists of components such as electricity imports (consumption) and exports back to the main grid [21][27][30][32][39][40][56][63][69][78]. In the case of a microgrid (MG), total cost minimization, investment, operation, and maintenance costs are considered. For instance, in [40][63], the optimization goal was to optimally size microgrid components (DG and ES) by shifting the load to the hours of maximum renewable penetration and therefore minimize total system costs. Some of the reviewed works also present different electricity tariffs based on the customer type (residential, commercial, or industrial).
Single objective with aggregated variables, weights, or penalties: In this case, more than one objective is combined and aggregated as a single function. In some works, weights are assigned to each optimization parameter, leading to a weighted single-objective optimization problem. In most cases, minimization of electricity costs, maximization of user convenience (appliance operational delay), and/or thermal comfort are considered, as in [19][23][38][41][42][43][48][58][64][65]. In a few research publications, such as in [43][65][80], three different objectives are weighted to form a single objective function. In other research works, the authors do not specify a weight factor, as in [35][59][61][62][73], but assign penalties to non-economic constraints in order to combine them into an aggregated single-objective function.
Multiple objectives: 
In [24][26][54][57][60][75], where objectives are conflicting, such as cost minimization and user convenience maximization, the Pareto front, meaning a set of non-dominated solutions, is calculated through the evaluation of different fitness functions that correspond to each objective. The Pareto front consists of compromise solutions. Therefore, a second step, in that case, would be the selection of the best solution from the Pareto set. Additionally, in this review work, bi-level optimization problems are characterized as multi-objective ones. In [45][46][50][66], there is a single “upper level” objective and a single “inner level” objective that need to be optimized hierarchically. The single upper-level objective is initially optimized, and then the output of the upper level is used as an input in the inner-level optimization.

2.2. Constraints

2.2.1. System Constraints

Part of the problem formulation in every work reviewed was to define the system constraints that should be considered in the optimization. The number of constraints differs depending on the system complexity and the type of energy resources considered. The main equality constraint, which can be identified in all works reviewed, is to maintain the energy balance between power supply and demand. The time period and the system boundaries (household, microgrid, or utility level) of such constraints depend on the problem formulation. The constraints that are identified in the reviewed works are the following:
  • Power grid thresholds (Egrid): The minimum and/or maximum contracted power of end-users with utility at the connection point. This increases the complexity of the optimization and potentially decreases the amount of energy savings that can be achieved since there is less flexibility to shift more loads to off-peak hours due to constraint violation.
  • Storage-related constraints (Estorage): Charging and discharging rates as well as the capacity of storage units are introduced as inequality constraints in works with energy storage, either in the form of batteries or in electric vehicles.
  • RES generation capacity (ERES): The maximum generation capacity of renewable sources is constrained, usually as a share of total household demand (e.g., 30% of net demand is met by RES).
  • User convenience: Another important consideration is user convenience in the sense of minimizing the operational delay (waiting time) of different household appliances or prioritizing the operation of appliances over others based on consumer preferences. In some works, such as [35], user convenience is introduced as the minimum amount of appliance switching needed during a DR event.
  • Thermal comfort: In many works, not only appliance waiting time but also indoor temperature and water heater temperature is considered when using thermostatically controlled loads. To operate appliances within the preferred temperature range, smart sockets and temperature sensors can be installed, as in [20].
  • Voltage level: In [35][37][63][73], bus or node voltage constraints are introduced when optimizing the operation of microgrids connected to the main power network.

2.2.2. Electricity Costs and User Convenience/Comfort

From the taxonomy of research work, based on optimization objectives and system constraints, it is clear that user convenience and thermal comfort are key considerations when trying to schedule and control residential resources. Operating according to user preferences will inevitably lead to higher electricity costs and vice versa. However, significant energy savings can still be obtained. In [20], using binary PSO (BPSO), 20–25% energy savings were achieved without jeopardizing user convenience. DR services were provided only in a specific timeframe (4–11 p.m.) in a geographical location with a lack of seasonality, so it would be worth testing the system under more challenging conditions. In [19][23][38][41][42][43][48][58][64][65], user convenience and energy savings were combined in the objective function, leading to a weighted single-objective optimization problem. User convenience was modeled with the use of allowed time periods when appliance operation should be completed. More specifically, in [19][23], GA and BPSO were compared, among others, where GA outperformed BPSO in terms of both electricity costs and energy consumption. In [25][29], the tradeoff between user convenience (appliance waiting time) and energy cost was investigated. PSO has the tendency to heavily shift loads from peak to off-peak hours with lower electricity tariffs in order to decrease electricity costs. However, a greater degree of user convenience is sacrificed in that case. Therefore, it can be concluded that the higher the electricity cost, the less the user discomfort, and vice versa in DR residential applications. While in [25], the single objective was to decrease consumer electricity costs, in [29], a single-objective function was formulated with the aim of minimizing energy costs and average-to-peak ratio. The feasible region of solutions was found, and boundaries were set for the objective function. In [27][30][31][52][56][76][77][78], reducing electricity bills while considering user convenience and thermal comfort was analyzed. The authors concluded that overall costs can be decreased without sacrificing user comfort by setting the indoor temperature at a higher level during low-tariff hours.

2.3. Applications

Each DSM model is characterized by the energy resources that can contribute to demand-side management, the number of users (single or multiple), and the control level (local, microgrid, or utility/aggregator). This review work focuses on residential users. The taxonomy of research works based on the application is illustrated in Figure 1.
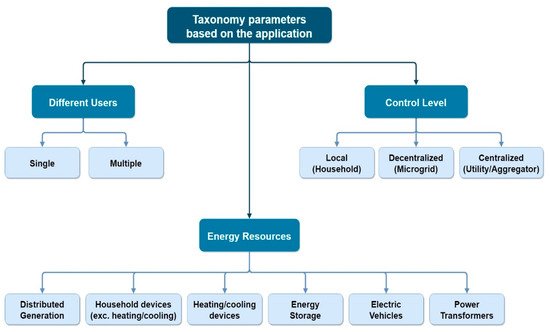
Energies 15 02211 g002 550
Figure 1. Taxonomy parameters based on the application.

2.3.1. Energy Systems

Scheduling and control of household appliances is the core focus in the majority of research works. Depending on the flexibility that these appliances can offer for demand-side management, they can be categorized as fixed, shiftable, elastic or interruptible, and power-adjustable. Fixed appliances are characterized by fixed power consumption and a length of operation that cannot be modified. Examples include lights, fans, clothing irons, microwave ovens, toasters, TVs, etc. The operation of shiftable appliances, such as washing machines, dishwashers, and clothes dryers, can be shifted in time but cannot be interrupted while their power consumption is fixed and inelastic. Elastic or interruptible household appliances, such as EVs, can not only be shifted in time but also be interrupted while in operation. This group of appliances can offer flexibility services by shifting their operation in periods of lower electricity tariffs. Last but not least, power-adjustable appliances are interruptible appliances with adjustable power consumption. The majority of these are thermostatically controlled loads (e.g., electric water heaters, ACs, or heat pumps). In research, the above categorization might differ based on the authors’ problem formulation. For instance, EVs can be treated as a shiftable but non-interruptible load in some works, while lights can be considered controllable when using a smart plug. In any case, when using interruptible and power-adjustable appliances for flexibility provision, it is important to ensure that user convenience and thermal comfort are not sacrificed when trying to schedule and control them for demand-side management.
In addition to residential appliances, decentralized energy resources such as EVs, distributed generation (mostly RES), and energy storage can contribute to domestic electricity bill reduction, load balance, and peak shaving. Additionally, a better tradeoff between user comfort and electricity cost reduction can be achieved, given that each household can utilize local or decentralized (microgrid) energy resources instead of consuming from the power grid. For instance, in [25], interruptible loads, including those of an EV and an electric water heater, contributed to achieving a better compromise between user convenience and energy costs. Although EVs are commonly treated as a highly flexible load, their battery-related constraints, such as the charging and discharging rate and maximum energy storage, can set limitations on its storage operation for demand-side management. It can also be observed that renewable power generation is often coupled with local energy storage, which aims at complementing the intermittency of renewable energy resources.

2.3.2. DR Programs - Electricity Tariffs

In addition to the objective function formulation and the constraints introduced for load scheduling, an important parameter is the type of DR program/mechanism that consumers are enrolled in. Time-of-use (ToU) retail tariffs have been extensively used in research, with prices usually ranging among high-, medium-, and low-price periods during the day. In some of the works where ToU is selected, it is highlighted that load is heavily shifted to off-peak hours. Therefore, the load tends to become unbalanced, with spikes occurring after these hours, and the peak-to-average ratio (PAR) remains high. A similar phenomenon can also be spotted when using day-ahead, real-time pricing (RTP) tariffs, which typically fluctuate on an hourly basis. For that reason, tariffs with inclined block rates (IBRs) were used in [19][29][36][41][45][48][81]. In this pricing scheme, when the load surpasses a certain level, a monetary penalty is added to the end-user’s electricity bill. In this way, load shifting from peak to off-peak hours is rather limited, PAR decreases, and load spikes are avoided.

2.4. Taxonomies

In Table 1, the reviewed works are classified based on the optimization objectives for residential load scheduling and control, together with modeling constraints. Table 2 presents the taxonomy of research work based on model applications, including DR programs.
Table 1. Taxonomy of the reviewed works based on the optimization objectives.
Refs Type of Constraints Objective Type Objectives
[16] Egrid + Estorage + User Convenience Single Electricity cost minimization
[19] Egrid + Estorage + ERES
+ User Convenience		 Single with weights Electricity cost minimization
+ user convenience maximization
[20] Thermal Comfort Single Energy consumption minimization
[21] Estorage Single Electricity cost minimization
[22][53] Estorage + User Convenience Single Electricity cost minimization
[23][41][64] User Convenience Single with weights Electricity cost minimization
+ user convenience maximization
[24] ERES Multiple (Pareto) Electricity cost minimization, distributing load across two energy sources (wind + solar) with different fitness functions
[25] ERES + User Convenience Single Electricity cost minimization
[26] Egrid + Estorage + ERES Multiple (Pareto) Electricity cost minimization +
Environmental cost (emissions) minimization
[27][30] Egrid + Estorage + Thermal Comfort
+ User Convenience		 Single Electricity cost minimization
[28] Egrid + ERES Single Electricity cost minimization
[29] Egrid + Estorage + User Convenience Single (aggregated objectives) Electricity cost minimization
+ PAR minimization
[31] Egrid + Estorage + ERES
+ Thermal Comfort + User Convenience		 Single Electricity cost minimization
[32] Egrid + Estorage Single Electricity cost minimization
[33] Egrid + ERES Single Consumer profit maximization
[34] Thermal Comfort + User Convenience Single Energy consumption minimization
[35] Voltage levels + User Convenience Single with penalties Electricity cost minimization + power loss cost minimization + constraints (penalties)
[36] Estorage + User Convenience Single (aggregated objectives) Electricity cost minimization
+ PAR minimization
[37] Egrid + Estorage + ERES + Voltage levels Single Distribution power loss minimization
[38] User Convenience Single with weights Electricity cost minimization + discomfort index minimization
[39] Egrid + Estorage Single Utility electricity cost minimization (DA, imbalance costs, and battery cycling cost)
[40] Estorage Single Total system cost minimization (incl. investments) to optimize minigrid components
[42] Egrid + User Convenience Single with weights Electricity cost minimization
+ user convenience maximization
[43] Egrid + Estorage + Thermal Comfort
+ User Convenience		 Single with weights Electricity cost minimization
+ user convenience maximization + grid load variance minimization (peak caused by DR actions)
[44] Estorage + Thermal Comfort Single Consumer profit maximization
[45] User Convenience Multiple (bi-level) Consumer profit maximization, after scheduling manually operated appliances with the worst impact on electricity payments
[46] Egrid + User Convenience Multiple (bi-level) Retailer profit maximization, after consumer electricity cost minimization
[47][79] - Single Electricity cost minimization
[48] Estorage + User Convenience Single with weights Electricity cost minimization
+ user convenience maximization
[49] Egrid + User Convenience Single Electricity cost minimization
[50] Estorage Multiple (bi-level) System cost minimization (NPC) + power shortage minimization
[51] Egrid + User Convenience Single (aggregated objectives) Electricity cost minimization + PAR minimization + user convenience maximization
[52] Egrid + Thermal Comfort
+ User Convenience		 Single Electricity cost minimization
[54] Estorage + ERES Multiple (Pareto) Electricity cost minimization + environmental cost/emission minimization
[55] Estorage + Thermal Comfort Single Flexibility potential estimation
[56][78] Estorage + Thermal Comfort
+ User Convenience		 Single Electricity cost minimization
[57] User Convenience Multiple (Pareto) Electricity cost minimization + load deviation minimization + user convenience maximization
[58] Estorage + Thermal Comfort
+ User Convenience		 Single with weights Electricity cost minimization (incl. battery degradation costs) + user comfort (incl. thermal and convenience)
[59] Egrid + Estorage Single with penalties Electricity cost minimization + DR curtailment minimization + Pmax violation (penalty)
[60] Egrid + User Convenience Multiple (Pareto) Electricity cost minimization + PAR minimization + CO2 minimization
[61] Estorage + Thermal Comfort Single with penalties Electricity cost minimization +
User comfort (penalties)
[62] User Convenience Single with penalties Utility electricity cost minimization for DR + consumer load interruptions (penalties)
[63] Egrid + Voltage levels + Estorage
+ User Convenience		 Single Total system cost minimization
[65] Estorage + User Convenience Single with weights Electricity cost minimization + user convenience maximization + CO2 minimization
[66] Egrid Multiple (bi-level) DNO operational cost minimization after MG operational cost minimization
[67][70] User Convenience Single Electricity cost minimization
[68] Thermal Comfort Single Electricity cost minimization
[69] Estorage + Thermal Comfort
+ User Convenience		 Single User comfort maximization
[71] Egrid + Estorage + ERES
+ Thermal Comfort + User Convenience		 Single (aggregated objectives) Electricity cost minimization + PAR minimization + user convenience maximization + CO2 minimization
[72] Egrid + User Convenience Single with weights Load deviation minimization + MG profit maximization
[73] Egrid + Voltage levels + Estorage Single with penalties Total system cost minimization + network loss minimization + constraints (penalty)
[74] Egrid + Estorage + Thermal Comfort Single Electricity cost minimization
[75] Egrid + Estorage + Thermal Comfort Multiple (Pareto) System cost minimization +
Environmental cost minimization
[76] Egrid + Estorage + Thermal Comfort
+ User Convenience		 Single Energy bill (electricity and gas) minimization
[77] Thermal Comfort + User Convenience Single Electricity cost minimization
[80] Estorage + ERES Single with weights Total system cost minimization + CO2 minimization + curtailed RES minimization
[81] User Convenience Single Electricity cost minimization (per appliance cluster)
Table 2. Taxonomy of the reviewed works based on the application.
Ref. No. Users Control Level Electricity Tariffs Energy Resources
[16][22][32] Single Local—Household ToU DG + energy storage +
household appliances (excl. heating/cooling)
[19] Multiple Local—Household ToU + IBR Heating/cooling + DG + energy storage +
Household appliances (excl. heating/cooling)
[20] Single Local—Household DLC Heating/cooling + household appliances (excl. heating/cooling)
[21] Multiple Decentralized—Microgrid RTP DG + energy storage
[23] Multiple Local—Household RTP Heating/cooling + household appliances (excl. heating/cooling)
[24] Single Local—Household - Heating/cooling + DG + household appliances (excl. heating/cooling)
[25] Single Local—Household ToU Heating/cooling + EV + DG + energy storage +
Household appliances (excl. heating/cooling)
[26][54] Multiple Decentralized—Microgrid Price-offer packages
(incentive-based)		 DG + energy storage
[27][69] Single Local—Household RTP Heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[28] Single Local—Household ToU EV + DG + energy storage +
household appliances (excl. heating/cooling)
[29] Multiple Local—Household +
Decentralized—Microgrid		 RTP + IBR Heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[30] Single Local—Household ToU Heating/cooling + EV + DG +
Household appliances (excl. Heating/cooling)
[31][56][76] Single Local—Household RTP Heating/cooling + energy storage +
household appliances (excl. heating/cooling)
[33] Multiple Decentralized—Microgrid Dynamic pricing based on RES generation DG
[34] Single Local—Household - Heating/cooling + household appliances (excl. heating/cooling)
[35] Multiple Centralized—
Utility or Aggregator		 Consumer bidding prices Power transformers + EV + household appliances (excl. heating/cooling)
[36][48] Single Local—Household RTP + IBR Heating/cooling + DG + energy storage +
Household appliances (excl. heating/cooling)
[37] Multiple Centralized—
Utility or Aggregator		 - Power transformers + DG + energy storage
[38][51][57][68] Single Local—Household ToU Heating/cooling +
household appliances (excl. heating/cooling)
[38][51][52][57][70] Single Local—Household RTP Heating/cooling +
household appliances (excl. heating/cooling)
[39] Multiple Decentralized—Microgrid - Heating/cooling + DG + energy storage
[40] Multiple Decentralized—
Standalone Microgrid		 - EV + DG + energy storage +
Household appliances (excl. heating/cooling)
[41] Single Local—Household RTP + IBR Heating/cooling + DG +
household appliances (excl. heating/cooling)
[42] Multiple Local—Household CPP, RTP Household appliances (excl. heating/cooling)
[43] Multiple Decentralized—Microgrid RTP Heating/cooling +
household appliances (excl. heating/cooling)
[44] Single Local—Household ToU, CPP Heating/cooling + EV + DG
[45] Single Local—Household RTP + IBR heating/cooling +
household appliances (excl. heating/cooling)
[46] Multiple Decentralized—Microgrid RTP Heating/cooling + EV +
household appliances (excl. heating/cooling)
[47][60][79] Multiple Centralized—
Utility or Aggregator		 RTP Household appliances (excl. heating/cooling)
[48] Single Local—Household ToU, CPP, RTP + IBR Heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[49] Single Local—Household RTP Household appliances (excl. heating/cooling)
[50] Multiple Decentralized—
Standalone Microgrid		 - heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[53][58][71] Single Local—Household RTP Heating/cooling + EV + DG + energy storage +
household appliances (excl. heating/cooling)
[55] Single Local—Household - Heating/cooling + DG + energy storage
[59] Multiple Centralized—
Utility or Aggregator		 ToU Heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[60] Multiple Centralized—
Utility or Aggregator		 ToU, CPP, RTP Household appliances (excl. heating/cooling)
[61] Multiple Local—Household RTP Heating/cooling + EV + energy storage
[62] Multiple Centralized—
Utility or Aggregator		 Load curtailment
(incentive-based)		 Household appliances (excl. heating/cooling)
[63] Multiple Centralized—
Utility or Aggregator		 Trip-reducing and
trip-shifting schemes
(incentive-based)		 Power transformers + EV + DG
[64] Single Local—Household RTP, ToU, load curtailment
(incentive-based)		 Heating/cooling + EV +
household appliances (excl. heating/cooling)
[65] Single Local—Household RTP Heating/cooling + EV + DG +
household appliances (excl. heating/cooling)
[66] Multiple Decentralized-—Microgrid RTP DG
[67] Single Local—Household ToU Household appliances (excl. heating/cooling)
[72] Multiple Decentralized—Microgrid - DG +
Household appliances (excl. heating/cooling)
[73] Multiple Decentralized—Microgrid - DG + energy storage +
household appliances (excl. heating/cooling)
[64][74] Single Local—Household ToU Heating/cooling + EV +
household appliances (excl. heating/cooling)
[75] Single Decentralized—Microgrid RTP Heating/cooling + DG + energy storage +
household appliances (excl. heating/cooling)
[77] Multiple Local—Household RTP Heating/cooling + DG +
household appliances (excl. heating/cooling)
[78] Multiple Decentralized—Microgrid RTP Heating/cooling + EV + DG + energy storage + household appliances (excl. heating/cooling)
[79] Multiple Centralized—
Utility or Aggregator		 RTP Household appliances (excl. heating/cooling)
[80] Multiple Decentralized—
Standalone Microgrid		 - DG + energy storage +
household appliances (excl. heating/cooling)
[81] Multiple Decentralized—Microgrid RTP + IBR Household appliances (excl. heating/cooling)

This entry is adapted from the peer-reviewed paper 10.3390/en15062211

References

  1. Shewale, A.; Mokhade, A.; Funde, N.; Bokde, N.D. An overview of demand response in smart grid and optimization techniques for efficient residential appliance scheduling problem. Energies 2020, 13, 4266.
  2. Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478.
  3. Pallonetto, F.; De Rosa, M.; D’Ettorre, F.; Finn, D.P. On the assessment and control optimisation of demand response programs in residential buildings. Renew. Sustain. Energy Rev. 2020, 127, 109861.
  4. Khan, A.A.; Razzaq, S.; Khan, A.; Khursheed, F.; Owais. HEMSs and enabled demand response in electricity market: An overview. Renew. Sustain. Energy Rev. 2015, 42, 773–785.
  5. Aghaei, J.; Alizadeh, M.I. Demand response in smart electricity grids equipped with renewable energy sources: A review. Renew. Sustain. Energy Rev. 2013, 18, 64–72.
  6. Georgilakis, S.P. Review of Computational Intelligence Methods for Local Energy Markets at the Power Distribution Level to Facilitate the Integration of Distributed Energy Resources: State-of-the-art and Future Research. Energies 2020, 13, 186.
  7. Rajasekhar, B.; Tushar, W.; Lork, C.; Zhou, Y.; Yuen, C.; Pindoriya, N.M.; Wood, K.L. A survey of computational intelligence techniques for air-conditioners energy management. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 555–570.
  8. Mabina, P.; Mukoma, P.; Booysen, M.J. Sustainability matchmaking: Linking renewable sources to electric water heating through machine learning. Energy Build. 2021, 246, 111085.
  9. Afram, A.; Sharifi, F.J. Gray-box modeling and validation of residential HVAC system for control system design. Appl. Energy 2015, 137, 134–150.
  10. Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sust. Energ. Rev. 2020, 130, 109899.
  11. Vazquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089.
  12. Zhang, Z.; Zhang, D. Deep reinforcement learning for power system application: An overview. CSEE J. Power Energy Syst. 2020, 6, 213–225.
  13. Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398.
  14. Merabet, G.H.; Essaaidi, M.; Ben Haddou, M.; Qolomany, B.; Qadir, J.; Anan, M.; Al-Fuqaha, A.; Riduan Abid, M.; Benhaddou, D. Intelligent building control systems for thermal comfort and energy-efficiency: A systematic review of artificial intelligence-assisted techniques. Renew. Sust. Energ. Rev. 2021, 144, 110969.
  15. Farzaneh, H.; Malehmirchegini, L.; Bejan, A.; Afolabi, T.; Mulumba, A.; Daka, P.P. Artificial intelligence evolution in smart buildings for energy efficiency. Appl. Sci. 2021, 11, 763.
  16. Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Azim Niaz, I. An Optimized Home Energy Management System with Integrated Renewable Energy and Storage Resources. Energies 2017, 10, 549.
  17. del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195.
  18. Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408.
  19. Rahim, S.; Javaid, N.; Ahmad, A.; Khan, S.A.; Khan, Z.A.; Alrajeh, N.; Qasim, U. Exploiting heuristic algorithms to efficiently utilize energy management controllers with renewable energy sources. Energy Build. 2016, 129, 452–470.
  20. Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Abd Ali, J. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227.
  21. Liu, D.; Xu, Y.; Wei, Q.; Liu, X. Residential energy scheduling for variable weather solar energy based on adaptive dynamic programming. IEEE/CAA J. 2018, 5, 36–46.
  22. Gudi, N.; Wang, L.; Devabhaktuni, V. A demand side management based simulation platform incorporating heuristic optimization for management of household appliances. Int. J. Electr. Power Energy Syst. 2012, 43, 185–193.
  23. Javaid, N.; Javaid, S.; Abdul, W.; Ahmed, I.; Almogren, A.; Alamri, A.; Niaz, I.A. A Hybrid Genetic Wind Driven Heuristic Optimization Algorithm for Demand Side Management in Smart Grid. Energies 2017, 10, 319.
  24. Lugo-Cordero, H.M.; Fuentes-Rivera, A.; Guha, R.K.; Ortiz-Rivera, E.I. Particle Swarm Optimization for load balancing in green smart homes. IEEE Congr. Evol. Comput. CEC 2011, 715–720.
  25. Javaid, N.; Ullah, I.; Akbar, M.; Iqbal, Z.; Ali Khan, F.; Alrajeh, N.; Alabed, M.S. An Intelligent Load Management System With Renewable Energy Integration for Smart Homes. IEEE Access 2017, 5, 13587–13600.
  26. Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Presenting a multi-objective generation scheduling model for pricing demand response rate in micro-grid energy management. Energy Convers. Manag. 2015, 106, 308–321.
  27. Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance Constrained Optimization in a Home Energy Management System. IEEE Trans Smart Grid 2018, 9, 252–260.
  28. Ullah, I.; Javaid, N.; Khan, Z.A.; Qasim, U.; Khan, Z.A.; Mehmood, S.A. An Incentive-based Optimal Energy Consumption Scheduling Algorithm for Residential Users. Procedia Comput. Sci. 2015, 52, 851–857.
  29. Javaid, N.; Hafeez, G.; Iqbal, S.; Alrajeh, N.; Alabed, M.S.; Guizani, M. Energy Efficient Integration of Renewable Energy Sources in the Smart Grid for Demand Side Management. IEEE Access 2018, 6, 77077–77096.
  30. Huang, Y.; Tian, H.; Wang, L. Demand response for home energy management system. Int. J. Electr. Power Ener. 2015, 73, 448–455.
  31. Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic Scheduling Mechanism for Smart Homes. Energies 2016, 9, 202.
  32. Faia, R.; Faria, P.; Vale, Z.; Spinola, J. Demand Response Optimization Using Particle Swarm Algorithm Considering Optimum Battery Energy Storage Schedule in a Residential House. Energies 2019, 12, 1645.
  33. Hassan, S.; Arshad, M.; Chen, M.; Lin, H.; Mohammed, A.; Mohammed, K.; Gohar Rehman, C. Optimization Modeling for Dynamic Price Based Demand Response in Microgrids. J. Clean. Prod. 2019, 222, 231–241.
  34. Ahmed, M.S.; Mohamed, A.; Homod, R.Z.; Shareef, H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies 2016, 9, 716.
  35. Rahman, M.M.; Arefi, A.; Shafiullah, G.M.; Hettiwatte, S. A new approach to voltage management in unbalanced low voltage networks using demand response and OLTC considering consumer preference. Int. J. Electr. Power Energy Syst. 2018, 99, 11–27.
  36. Hafeez, G.; Javaid, N.; Iqbal, S.; Khan, F.A. Optimal Residential Load Scheduling Under Utility and Rooftop Photovoltaic Units. Energies 2018, 11, 611.
  37. Ziadi, Z.; Taira, S.; Oshiro, M.; Funabashi, T. Optimal Power Scheduling for Smart Grids Considering Controllable Loads and High Penetration of Photovoltaic Generation. IEEE Trans. Smart Grid 2014, 5, 2350–2359.
  38. Rezaee Jordehi, A. Binary particle swarm optimisation with quadratic transfer function: A new binary optimisation algorithm for optimal scheduling of appliances in smart homes. Appl. Soft Comput. 2019, 78, 465–480.
  39. Correa-Flórez, C.G.; Gerossier, A.; Michiorri, A.; Kariniotakis, G. Stochastic operation of home energy management systems including battery cycling. Appl. Energy 2018, 225, 1205–1218.
  40. Mohseni, S.; Moghaddas-Tafreshi, S.M. A multi-agent system for optimal sizing of a cooperative self-sustainable multi-carrier microgrid. Sustain. Cities Soc. 2018, 38, 452–465.
  41. Lin, Y.-H.; Hu, Y.-C. Residential Consumer-Centric Demand-Side Management Based on Energy Disaggregation-Piloting Constrained Swarm Intelligence: Towards Edge Computing. Sensors 2018, 18, 1365.
  42. Javaid, N.; Ahmed, F.; Ullah, I.; Abid, S.; Abdul, W.; Alamri, A.; Almogren, A.S. Towards Cost and Comfort Based Hybrid Optimization for Residential Load Scheduling in a Smart Grid. Energies 2017, 10, 1546.
  43. Zhu, J.; Lin, Y.; Lei, W.; Liu, Y.; Tao, M. Optimal household appliances scheduling of multiple smart homes using an improved cooperative algorithm. Energy 2019, 171, 944–955.
  44. Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Coordinated Scheduling of Residential Distributed Energy Resources to Optimize Smart Home Energy Services. IEEE Trans. Smart Grid 2010, 1, 134–143.
  45. Du, Y.F.; Jiang, L.; Li, Y.; Wu, Q. A Robust Optimization Approach for Demand Side Scheduling Considering Uncertainty of Manually Operated Appliances. IEEE Trans. Smart Grid 2018, 9, 743–755.
  46. Carrasqueira, P.; Alves, M.J.; Antunes, C.H. Bi-level particle swarm optimization and evolutionary algorithm approaches for residential demand response with different user profiles. Inf. Sci. 2017, 418–419, 405–420.
  47. Faria, P.; Vale, Z.; Soares, J.; Ferreira, J. Demand Response Management in Power Systems Using Particle Swarm Optimization. IEEE Intell. Syst. 2013, 28, 43–51.
  48. Hussain, B.; Khan, A.; Javaid, N.; Hasan, Q.U.; Malik, S.A.; Ahmad, O.; Dar, A.H.; Kazmi, A. A Weighted-Sum PSO Algorithm for HEMS: A New Approach for the Design and Diversified Performance Analysis. Electronics 2019, 8, 180.
  49. Khan, A.; Javaid, N.; Ahmad, A.; Akbar, M.; Khan, Z.A.; Ilahi, M. A priority-induced demand side management system to mitigate rebound peaks using multiple knapsack. J. Ambient Intell. Humaniz. Comput. 2019, 10, 1655–1678.
  50. Jing, Z.; Zhu, J.; Hu, R. Sizing optimization for island microgrid with pumped storage system considering demand response. J. Mod. Power Syst. Clean Energy 2018, 6, 791–801.
  51. Hafeez, G.; Wadud, Z.; Khan, I.U.; Khan, I.; Shafiq, Z.; Usman, M.; Khan, M.U.A. Efficient Energy Management of IoT-Enabled Smart Homes Under Price-Based Demand Response Program in Smart Grid. Sensors 2020, 20, 3155.
  52. Wang, J.; Li, Y.; Zhou, Y. Interval number optimization for household load scheduling with uncertainty. Energy Build 2016, 130, 613–624.
  53. Imran, A.; Hafeez, G.; Khan, I.; Usman, M.; Shafiq, Z.; Qazi, A.B.; Khalid, A.; Thoben, K.D. Heuristic-Based Programable Controller for Efficient Energy Management Under Renewable Energy Sources and Energy Storage System in Smart Grid. IEEE Access 2020, 8, 139587–139608.
  54. Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Demand side management in a smart micro-grid in the presence of renewable generation and demand response. Energy 2017, 126, 622–637.
  55. Pinto, R.; Bessa, R.J.; Matos, M.A. Multi-period flexibility forecast for low voltage prosumers. Energy 2017, 141, 2251–2263.
  56. Huang, Y.; Wang, W.; Hou, B. A hybrid algorithm for mixed integer nonlinear programming in residential energy management. J. Clean. Prod. 2019, 226, 940–948.
  57. Khan, Z.A.; Khalid, A.; Javaid, N.; Haseeb, A.; Saba, T.; Shafiq, M. Exploiting Nature-Inspired-Based Artificial Intelligence Techniques for Coordinated Day-Ahead Scheduling to Efficiently Manage Energy in Smart Grid. IEEE Access 2019, 7, 140102–140125.
  58. Zhang, Y.; Zeng, P.; Li, S.; Zang, C.; Li, H. A Novel Multiobjective Optimization Algorithm for Home Energy Management System in Smart Grid. Math. Probl. Eng. 2015, 2015, 807527.
  59. Lezama, F.; Faia, R.; Faria, P.; Vale, Z. Demand Response of Residential Houses Equipped with PV-Battery Systems: An Application Study Using Evolutionary Algorithms. Energies 2020, 13, 2466.
  60. Nawaz, A.; Hafeez, G.; Khan, I.; Jan, K.U.; Li, H.; Ali Khan, S.; Wadud, Z. An Intelligent Integrated Approach for Efficient Demand Side Management with Forecaster and Advanced Metering Infrastructure Frameworks in Smart Grid. IEEE Access 2020, 8, 132551–132581.
  61. Sisodiya, S.; Shejul, K.; Kumbhar, G.B. Scheduling of demand-side resources for a building energy management system. Int. Trans. Electr. Energy Syst. 2017, 29, e2369.
  62. Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Scheduling of Demand Side Resources Using Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2009, 24, 1173–1181.
  63. Soares, J.; Morais, H.; Sousa, T.; Vale, Z.; Faria, P. Day-Ahead Resource Scheduling Including Demand Response for Electric Vehicles. IEEE Trans. Smart Grid 2013, 4, 596–605.
  64. Rezaee Jordehi, A. Enhanced leader particle swarm optimisation (ELPSO): A new algorithm for optimal scheduling of home appliances in demand response programs. Artif. Intell. Rev. 2020, 53, 2043–2073.
  65. Ma, K.; Hu, S.; Yang, J.; Xu, X.; Guan., X. Appliances scheduling via cooperative multi-swarm PSO under day-ahead prices and photovoltaic generation. Appl. Soft Comput. 2018, 62, 504–513.
  66. Zhang, H.; Zhao, D.; Gu, C.; Li, F.J. Bilevel economic operation of distribution networks with microgrid integration. Renew. Sustain. Energy 2015, 7, 023120.
  67. Chellamani, G.K.; Chandramani, P.V. An Optimized Methodical Energy Management System for Residential Consumers Considering Price-Driven Demand Response Using Satin Bowerbird Optimization. J. Electr. Eng. Technol. 2020, 15, 955–967.
  68. Parvin, K.; Hannan, M.A.; Al-Shetwi, A.Q.; Ker, P.J.; Roslan, M.F.; Mahlia, T.M.I. Fuzzy Based Particle Swarm Optimization for Modeling Home Appliances Towards Energy Saving and Cost Reduction Under Demand Response Consideration. IEEE Access 2020, 8, 210784–210799.
  69. Wang, L.; Wang, Z.; Yang, R. Intelligent Multiagent Control System for Energy and Comfort Management in Smart and Sustainable Buildings. IEEE Trans. Smart Grid 2012, 3, 605–617.
  70. Gudi, N.; Wang, L.; Devabhaktuni, V.; Depuru, S.S.S.R. Demand response simulation implementing heuristic optimization for home energy management. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–6.
  71. Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An Optimal Power Usage Scheduling in Smart Grid Integrated With Renewable Energy Sources for Energy Management. IEEE Access 2021, 9, 84619–84638.
  72. Ebrahimi, J.; Abedini, M.; Rezaei, M.M. Optimal scheduling of distributed generations in microgrids for reducing system peak load based on load shifting. Sustain. Energy Grids Netw. 2020, 23, 100368.
  73. Li, P.; Xu, D.; Zhou, Z.; Lee, W.J.; Zhao, B. Stochastic Optimal Operation of Microgrid Based on Chaotic Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2016, 7, 66–73.
  74. Zhang, Z.; Wang, J.; Zhong, H.; Ma, H. Optimal scheduling model for smart home energy management system based on the fusion algorithm of harmony search algorithm and particle swarm optimization algorithm. Sci. Technol. Built. Environ. 2019, 26, 42–51.
  75. Esmaeili, S.; Jadid, S. Economic-Environmental Optimal Management of Smart Residential Micro-Grid Considering CCHP System. Electr. Power Compon. Syst. 2019, 46, 1592–1606.
  76. Huang, Y.; Zhang, J.; Mo, Y.; Lu, S.; Ma, J. A Hybrid Optimization Approach for Residential Energy Management. IEEE Access 2020, 8, 225201–225209.
  77. Javaid, S.; Javaid, N. Comfort evaluation of seasonally and daily used residential load in smart buildings for hottest areas via predictive mean vote method. Sustain. Comput. Inform. Syst. 2020, 25, 100369.
  78. Kanakadhurga, D.; Prabaharan, N. Demand response-based peer-to-peer energy trading among the prosumers and consumers. Energy Rep. 2021, 7, 7825–7834.
  79. Zeeshan, M.; Jamil, M. Adaptive Moth Flame Optimization based Load Shifting Technique for Demand Side Management in Smart Grid. IETE J. Res. 2021, 1–12.
  80. Chen, H.; Gao, L.; Zhang, Z.; Li, H. Optimal Energy Management Strategy for an Islanded Microgrid with Hybrid Energy Storage. J. Electr. Eng. Technol. 2021, 16, 1313–1325.
  81. Abbasi, A.; Sultan, K.; Aziz, M.A.; Khan, A.U.; Khalid, H.A.; Guerrero, J.M.; Zafar, B.A. A Novel Dynamic Appliance Clustering Scheme in a Community Home Energy Management System for Improved Stability and Resiliency of Microgrids. IEEE Access 2021, 9, 142276–142288.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback