The motion state of quadruped robot in operation changes constantly. Due to the drift caused by the accumulative error, the function of inertial measurement unit (IMU) will be limited. Even though multi-sensor fusion technology is adopted, the quadruped robot will lose its ability to respond to state changes after a while because the gain tends to be constant. To solve this problem, this paper proposes a Strong Tracking Mixed-degree Cubature Kalman Filter (STMCKF) method. According to system characteristics of the quadruped robot, this method makes fusion estimation of forward kinematics and IMU track. The combination mode of Traditional Strong Tracking CKF (TSTCKF) and strong tracking is improved through demonstration. A new method for calculating fading factor matrix is proposed, which reduces sampling times from three to one, saving 66% of calculation time. At the same time, the state estimation accuracy is improved from third-degree accuracy of Taylor series expansion to fifth-degree accuracy. The proposed algorithm can automatically switch the working mode according to real-time supervision of the motion state and greatly improve the state estimation performance of quadruped robot system, exhibiting strong robustness and excellent real-time performance.
- Quadruped robot
- State Estimation
- STMCKF
- IMU
- Kinematics
1. Introduction
A legged robot has broad application prospects owing to its strong ability to pass through complex ground without continuous support. To let a quadruped robot gain strong autonomous motion capability, the state estimation of a quadruped robot is a challenge, that is, the robot needs to accurately estimate its state information (position, velocity, attitude) before performing each action, and only in this way can the right decisions be made for the next motion. The inertial measurement unit (IMU) can calculate the state information through the built-in accelerometer and gyroscope, which has been used in almost all mobile robots due to its advantages of good concealment, high short-term accuracy and less susceptibility to environmental interference. However, a long-term use of IMU will cause accumulated error, leading to a drift of calculation results. Some errors are unavoidable in IMU of various levels, which need to be addressed by additional correction measures. Multi-sensor fusion technology offers a solution to this problem. There are mainly two commonly used methods. One is to add additional sensors, such as GPS, camera, which relies on specific external references. However, the information accuracy is prone to environmental interference and the newly added sensors have high requirements for communication and computing equipment, resulting in increased cost and poor reliability. The other method, which does not need additional sensors, is to redevelop the application potential of the system’s own sensors and acquire state information using a forward kinematics solution. This method does not lead to increased cost or accumulated errors, nor require additional communication and computing equipment support, so the implementation is easy. The internal sensor has a low short-term accuracy although it is not affected by the environment. A reasonable idea is to integrate it with IMU to give play to their advantages while abandoning the disadvantages of the two. The fusion effect is mainly determined by a fusion algorithm. Therefore, research on fusion algorithm carries great significance for the development of quadruped robots.
A quadruped robot is basically a non-linear system. The fusion algorithm commonly used in engineering for non-linear systems is extended Kalman filter (EKF)[1]. As it is based on classical Kalman and obtained by solving a Jacobian matrix from an equation of state and observation equation, the principle is simple, easy to understand and easy to realize. EKF also requires calculation of Jacobian matrix, and it is only applicable to weakly nonlinear systems. Moreover, its accuracy is merely equal to first-degree accuracy of Taylor expansion. However, the excellent real-time performance makes it widely used in various non-linear systems including quadruped robots. The unscented Kalman filter (UKF)[2], particle filter (PF)[3] and cubature kalman filter (CKF)[4] represent other types of common non-linear filters with common characteristics. Their common feature is that they all use sampling points to approximately approach non-linear equations. Generally speaking, a larger number of sampling points means better fitness with the non-linear function, and also means higher estimation accuracy. However, the calculation amount of the algorithm is mainly determined by the number of sampling points. Improving accuracy and increasing real-time performance mean a set of contradictory propositions, so these three algorithms have higher accuracy and calculation amount than EKF. There are no uniform UKF sampling strategies and many parameters need to be adjusted manually, so algorithm performance is mainly determined by prior knowledge. PF utilizes a large number of sampling particles in exchange for high estimation accuracy, but its tremendous calculation amount makes it difficult to meet the requirements of online use. CKF is essentially a UKF with a unified sampling strategy, so it has a calculation amount basically comparable to UKF, and can reach third-degree truncation accuracy of Taylor series expansion. Because of its strict mathematical derivation, according to the third-degree spherical diameter volume rule, 2n volume points with the same weight of 1/2n are sampled on the hypersphere surface with variance; for instance, the number is 18 points for a quadruped robot system with a 9-dimensional state equation. It guarantees that the covariance matrix is always a positive definite matrix while avoiding the divergence problem caused by non-positive definiteness of the covariance matrix, so the numerical stability is higher compared to UKF. Gupta D et al.[5] pointed out that CKF has better filtering accuracy than UKF with three-dimensional systems and above. To further improve the accuracy, higher-degree versions such as fifth-degree CKF[6] and seventh-degree CKF[7] have been proposed successively. Although an arbitrary degree CKF is possible in theory, the number of sampling points is required to increase gradually with the continuous improvement of estimation accuracy. The fifth-degree CKF requires 2n2+1 volume points, and the 9-dimensional system requires 163 volume points. The seventh-degree CKF requires n3+9n2+14n+6 volume points, and the 9-dimensional system requires 1590 volume points. It can be seen that although higher degree CKF allows higher estimation accuracy, the number of volume points increases rapidly with the increase of degree. Moreover, CKF of each degree inherits shortcomings of KF and depends more on the initial value. The symmetry and non-negative definiteness of the covariance matrix can sometimes undermine the estimation effect and easily lead to filter divergence. To ensure the symmetry and non-negative definiteness of the covariance matrix and effectively avoid the problem of filter divergence, a square root volume Kalman filter (SRCKF)[8] directly performs recursive updating in the form of square root of the covariance matrix during the filtering process, which can effectively improve numerical stability of filter. To further reduce calculation complexity and achieve higher calculation efficiency, Cui et al.[9] proposed a state of charge (SOC) estimation algorithm based on SRCKF. SRCKF approximates the average of the state variables by calculating 2n points with the same weight according to the cubic transformation. After these points are propagated by the non-linear function, the mean value and variance can reach the third-degree accuracy of the real value of the non-linear function. SRCKF directly propagates and updates the square root of the covariance matrix in the form of Cholesky decomposition, which guarantees the non-negative property of the covariance matrix and avoids the divergence of the filter. Wang et al.[10] proposed SSRCKF by adopting the simplest phase-diameter sampling rule. Compared with the traditional volumetric sampling method, it demonstrates simpler calculation and higher accuracy. Liu et al.[11] proposed a interacting multiple model fifth-degree spherical simplex-radial cubature Kalman filter (IMM5thSSRCKF) by integrating the interacting multiple model (IMM) filter with the fifth-degree spherical simplex-radial cubature Kalman filter (5thSSRCKF). Wang et al.[12] proposed a mixed-degree spherical simple-x-radial cubature Kalman filter (MSSRCKF), and analyzed its accuracy. Simulations results showed that the algorithm can achieve performance improvement of fifth-degree SSRCKF and has higher accuracy under less computational burden. The MSSRCKF collects 2n+3 volume points based on the third-degree surface integrals and fifth-degree radial integrals, which requires only three more volume points than the standard CKF, but achieves an accuracy approaching to the fifth-degree CKF[13]. In the 9-dimensional system, only 21 volume points are required, which saves 142 points for each volume point sampling compared to the fifth-degree CKF. Although it is also reasonable to combine the fifth-degree spherical integral and the third-degree radial integral, n2+3n+2 volume points are required, which means, 110 volume points are required in a 9-dimensional system. Hence, MSSRCKF is more suitable for a quadruped robot system.
A quadruped robot is also a time-varying system, whose motion state often changes suddenly. The state equation established based on quadruped robot inertial navigation system is often a highly non-linear high-dimensional time-varying system. To obtain state information accurately in the presence of frequently changed motion state, the filter demands strong robustness and fast convergence speed. Strong tracking[14] is a method that is very suitable for combined use with other filters to improve robust performance of the original filter. Since its inception, it has been incorporated with EKF, known as the strong tracking extended Kalman filter (STEKF)[14]. By introducing fading factor into the state prediction covariance matrix, it adjusts the gain matrix online in real time, and forces the filtering residual sequences to remain mutually orthogonal. In this way, STF can still keep track of the system state when the system model is uncertain, which effectively solves the problems of poor robustness and filtering divergence of EKF under uncertainties. Feng et al.[15]combined strong tracking filtering (STF)[14] with the seventh-degree SSRCKF to obtain higher accuracy. Huang et al.[16] combined strong tracking theory with CKF to solve the problem of spacecraft attitude estimation, but the algorithm demands three times of volume point sampling calculations. Hua et al.[17] proposed the strong tracking spherical simplex-radial CKF (STSSRCKF) algorithm to deal with sudden changes of the target state. However, the shortcoming is that the single fading factor was used and three times of volume p[18]oint sampling calculations were still required. Zhao et al. proposed the adaptive robust square-root CKF (ARSCKF) algorithm by combining strong tracking theory with SRCKF, However, due to the lack of rigorous derivation and proof to truly satisfy the orthogonality of novelty sequences, it was also necessary to carry out the calculation of cubic volume point sampling. Such traditional strong tracking CKF (TSTCKF) requires three volume point samplings for each filtering[19]. Zhang et al.[19] discussed the calculation method and addition of the location of the fading factor in detail and then proposed the normal strong tracking CKF (NSTCKF) and fast strong tracking CKF (FSTCKF). However the shortcoming is that both algorithms only adopted a single fading factor and the calculation of Jacobian matrix was still required. Although FSTCKF requires only two volume point samplings, compensation is unnecessary for observation prediction. It can be seen that these previous methods combined with strong tracking are basically based on SFEKF combination, and EKF does not need sampling point calculation, but UKF and CKF and some improved algorithms require sampling point calculation, which makes sampling times increase from two to three for each filtering process, which significantly increases the calculation amount and thereby hider the application of quadruped robots. In order to solve the problem in the above analyses, a Strong Tracking Mixed-degree Cubature Kalman Filter algorithm is proposed. According to the structural characteristics of the quadruped robot, the forward kinematics dead reckoning of the robot is obtained in real time through the linear displacement sensor, and the results of the forward kinematics dead reckoning with the IMU are filtered through the fusion of STMCKF, and then fusion results are used to correct the IMU. Through demonstrating correct combination of strong tracking and CKF-type algorithms, the calculation method of fading factor matrix is improved, and sampling times per filter of TSTCKF is reduced from three to one. Since no additional external sensors are added, external environmental interference is avoided. In this way, the quadruped robot system using this algorithm can significantly improve state estimation accuracy, real-time performance and robustness without increasing research and development costs. The improved STMCKF has fifth-degree accuracy, strong robustness and good real-time performance, which only needs one sampling point calculation.
2. Numerical Experiments
Figure 1. Screenshot of walking experiment of quadruped robot prototype.
Figure 1 is a video screenshot of a quadruped robot walking with STMCKF. It can be seen from the figure that when a pair of diagonal legs are in stable supporting posture, the robot mass center will move forward and the whole process is stable. The correctness and validity of the STMCKF proposed in this paper are proved again by experiments.
(a) (b)
(c) (d)
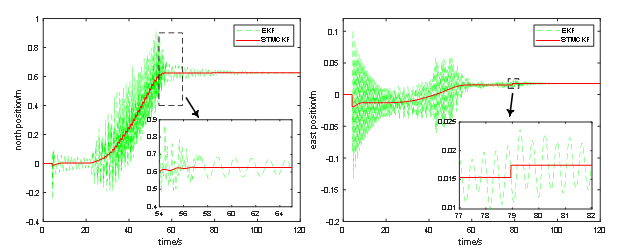
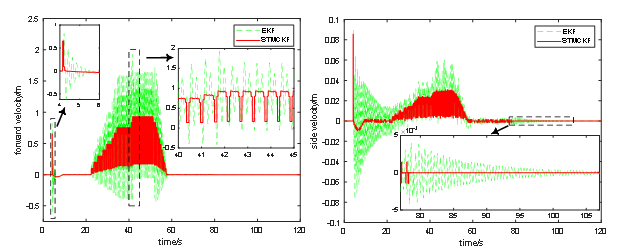
Figure 2. Comparison of state estimation between EKF and STMCKF of a quadruped robot.
In Figure 2, the red full line represents STMCKF estimation, and green dash line represents EKF estimation. According to Figure 2, it can be seen that it takes about 4s for the robot to start up and complete initialization, which is consistent with the actual situation. After resetting each foot, the sudden change of the position and velocity of the robot body in all directions will occur, STMCKF and EKF both respond to the sudden change of the robot's motion state, indicating high sensitivity of the two. However, from the estimation curve, it can be seen that STMCKF converges more rapidly than EKF, and the response amplitude of STMCKF is significantly smaller than EKF, indicating that STMCKF has a strong resistance effect to sudden change of motion state. These results prove that STMCKF is better than EKF in coping with the sudden change of motion state. In Figure 2 (a) and Figure 2 (b), the time-varying curves of the robot's north and east position are depicted. It can be seen that the solid line representing STMCKF presents a regular change with time, indicating that the STMCKF estimation results are accurate. The state switching during 21s ~ 22s and 56s ~ 58s is smooth and fast, which shows that STMCKF has a strong tracking ability to the motion state and the application of STMCKF can effectively improve the accuracy and stability of positioning and navigation.
As shown in Figure. 2 (a) and Figure. 2 (b), the dotted line representing EKF responds to the sudden change at 4s and shows a trend of convergence although it does not fully converge until 21s. As the robot moves forward, the original convergence trend of EKF becomes the divergence trend and then the robot moves rhythmically, so that the motion state will constantly change and the divergence trend of EKF will no more converge. In Figure 2 (c) and Figure 2 (d), the time-varying curves of the robot's forward and side velocity are depicted. Figure 2 (c) shows that STMCKF converges rapidly in 0.05s after responding to the sudden change of forward speed caused by robot start-up, while EKF converges successfully in 2s. And it can be seen that the robot stops walking after 57s. The forward velocity of the robot returns to zero, but the lateral speed changes within a very small range in Figure 2 (d). That is to say, the robot swings slightly independently to maintain the balance. Instead of swinging back and forth, the robot swings laterally to maintain the balance, which is in line with our bionic design. Since the robot cannot completely calm down after walking, the change of its velocity is notified to the robot control center via STMCKF. Finally, the control center decides to shift 2.2mm eastward to keep balance. It can be seen from Figure 2 (d) that after the robot moves 2.2mm eastward, its lateral velocity basically returns to zero. This shows the role of STMCKF in adjusting the motion state of the robot.
When the walking velocity of the robot is accelerating from zero to the expected velocity of 1m/s, the estimated results of EKF show a obvious divergent trend, and the amplitude is very large. The estimation velocity of EKF is much higher than the expected velocity, with negative velocity even occurred, which is obviously incorrect. Furthermore, it can be seen from the local enlarged figure of 40s ~ 45s that the curve of EKF's forward velocity estimation is sharp, indicating the velocity often changes abruptly, which is very unfavorable for the control of the quadruped robot. Using such a state estimator will make the track of the foot end of the robot become not so smooth, increasing the wear of various components and reducing the service life. The velocity estimation curve plotted by STMCKF shows a regular periodic sawtooth wave, and the peak value of velocity is very close to 1m/s. This may be because the ground on which the robot walks is made of smooth tile, so the slipping phenomenon occurred, which reduced the walking efficiency.
For systems where equation of state is non-linear, TSTCKF requires three volume point calculations for each filtering, but STMCKF only needs one volume point calculation for each filtering. The accuracy of STMCKF is several times higher than that of EKF while the time consumption of STMCKF is only 37% longer than that of EKF. For the sudden change of robot motion state, STMCKF can also make accurate judgment, effective suppression and strong tracking. To sum up, STMCKF is very suitable for the quadruped robot system whose motion state changes constantly. Using the STMCKF algorithm, the state estimation accuracy of quadruped robots can be effectively improved without increasing the R&D cost. Moreover, the proposed algorithm has good robustness and real-time performance, making the sensor on the robot achieve the maximum use benefit. Meanwhile, since there is no limitation to the number of feet, STMCKF is suitable for all legged robots, which has great application value for improving the motion performance of legged robot and for enhancing the accuracy of navigation and positioning.
References
- Yaakov, B.S.; Li, X.; Thiagalingam, K. Estimation with Applications to Tracking and Navigation, John Wiley and Sons: New York, NY, USA, 2001.
- Julier, S. J.; Uhlmann, J. K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401-422.
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208.
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269.
- Gupta, D.; Anand, R. S.; Tyagi, B. Ripplet domain non-linear filtering for speckle reduction in ultrasound medical images. Biomed. Signal Process. Control 2014, 10, 79–91.
- JIA, B.; XIN, M.; CHENG, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518.
- Meng, D.; Miao, L.; Shao, H. A Seventh-Degree Cubature Kalman Filter. Asian J. Control 2017, 20, 250–262.
- Yanling, H.; Junwei, Y.; Liang, C. Square Root Cubature Kalman Filter. J. Projectiles Rockets Missiles Guidance 2012, 32, 169–172.
- Cui, X.; Jing, Z.; Luo, M.; Guo, Y.; Qiao, H. A New Method for State of Charge Estimation of Lithium-Ion Batteries Using Square Root Cubature Kalman Filter. Energies 2018, 11, 209–.
- Wang, S.; Feng, J.; Tse, C. K. Spherical Simplex-Radial Cubature Kalman Filter. IEEE Signal Process Lett. 2014, 21, 43–46.
- Liu, H.; Wu, W. Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2017, 17, 1374–.
- Wang, S.; Feng, Y.; Duan, S.; Wang, L. Mixed-Degree Spherical Simplex-Radial Cubature Kalman Filter. Math. Prob. Eng.2017, 10, 23–29.
- Zhang, Y.; Huang, Y.; Wu, Z.; Li, N. Seventh-degree spherical simplex-radial cubature Kalman filter. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28-30 July 2014, 7, 2513–2517.
- Zhou, D. H.; Xi, Y. G.; Zhang, Z. J. A suboptimal multiple fading extended Kalman filter. Acta Autom. Sin 1991, 17, 689–695.
- Feng, K.; Li, Jie.; Zhang, X.; Zhang, X.; Shen, C.; Cao, H.; Yang, Y.; Liu, W. An Improved Strong Tracking Cubature Kalman Filter for GPS/INS Integrated Navigation Systems. Sensors 2018, 18, 1919–.
- Huang, W.; Xie, H.; Shen, C.; Li, J. A robust strong tracking cubature Kalman filter for spacecraft attitude estimation with quaternion constraint. Acta Astronautica 2016, 121, 153–163.
- Hua, L.; Wen, W. Strong Tracking Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2017, 17, 741-753.
- Zhao, L.; Wang, J.; Yu, T.; Jian, H.; Liu, T. Design of adaptive robust square-root cubature Kalman filter with noise statistic estimator. Appl. Math. Comput. 2015, 256, 352–367.
- Zhang, A.; Bao, S.; Gao, F.; Bi, W. A novel strong tracking cubature Kalman filter and its application in maneuvering target tracking. Chin. J. Aeronaut. 2019, 32, 2489–2502.