The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the vernal equinox, and a right-handed convention. The origin at the centre of Earth means the coordinates are geocentric, that is, as seen from the centre of Earth as if it were transparent. The fundamental plane and the primary direction mean that the coordinate system, while aligned with Earth's equator and pole, does not rotate with the Earth, but remains relatively fixed against the background stars. A right-handed convention means that coordinates increase northward from and eastward around the fundamental plane.
- vernal
- coordinate system
- equatorial
1. Primary Direction
This description of the orientation of the reference frame is somewhat simplified; the orientation is not quite fixed. A slow motion of Earth's axis, precession, causes a slow, continuous turning of the coordinate system westward about the poles of the ecliptic, completing one circuit in about 26,000 years. Superimposed on this is a smaller motion of the ecliptic, and a small oscillation of the Earth's axis, nutation.[1]
In order to fix the exact primary direction, these motions necessitate the specification of the equinox of a particular date, known as an epoch, when giving a position. The three most commonly used are:
- Mean equinox of a standard epoch (usually J2000.0, but may include B1950.0, B1900.0, etc.)
- is a fixed standard direction, allowing positions established at various dates to be compared directly.
- Mean equinox of date
- is the intersection of the ecliptic of "date" (that is, the ecliptic in its position at "date") with the mean equator (that is, the equator rotated by precession to its position at "date", but free from the small periodic oscillations of nutation). Commonly used in planetary orbit calculation.
- True equinox of date
- is the intersection of the ecliptic of "date" with the true equator (that is, the mean equator plus nutation). This is the actual intersection of the two planes at any particular moment, with all motions accounted for.
A position in the equatorial coordinate system is thus typically specified true equinox and equator of date, mean equinox and equator of J2000.0, or similar. Note that there is no "mean ecliptic", as the ecliptic is not subject to small periodic oscillations.[2]
2. Spherical Coordinates
2.1. Use in Astronomy
A star's spherical coordinates are often expressed as a pair, right ascension and declination, without a distance coordinate. The direction of sufficiently distant objects is the same for all observers, and it is convenient to specify this direction with the same coordinates for all. In contrast, in the horizontal coordinate system, a star's position differs from observer to observer based on their positions on the Earth's surface, and is continuously changing with the Earth's rotation.
Telescopes equipped with equatorial mounts and setting circles employ the equatorial coordinate system to find objects. Setting circles in conjunction with a star chart or ephemeris allow the telescope to be easily pointed at known objects on the celestial sphere.
2.2. Declination
The declination symbol δ, (lower case "delta", abbreviated DEC) measures the angular distance of an object perpendicular to the celestial equator, positive to the north, negative to the south. For example, the north celestial pole has a declination of +90°. The origin for declination is the celestial equator, which is the projection of the Earth's equator onto the celestial sphere. Declination is analogous to terrestrial latitude.[3][4][5]
2.3. Right Ascension
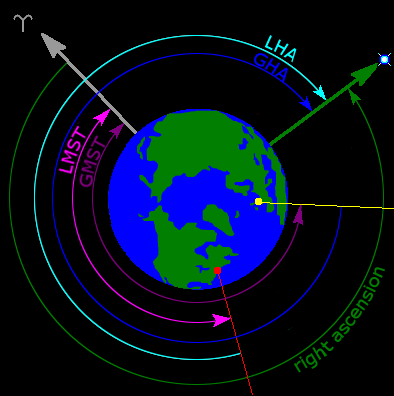
The right ascension symbol α, (lower case "alpha", abbreviated RA) measures the angular distance of an object eastward along the celestial equator from the vernal equinox to the hour circle passing through the object. The vernal equinox point is one of the two points where the ecliptic intersects the celestial equator. Right ascension is usually measured in sidereal hours, minutes and seconds instead of degrees, a result of the method of measuring right ascensions by timing the passage of objects across the meridian as the Earth rotates. There are 360°/24h = 15° in one hour of right ascension, and 24h of right ascension around the entire celestial equator.[3][6][7]
When used together, right ascension and declination are usually abbreviated RA/Dec.
2.4. Hour Angle
Alternatively to right ascension, hour angle (abbreviated HA or LHA, local hour angle), a left-handed system, measures the angular distance of an object westward along the celestial equator from the observer's meridian to the hour circle passing through the object. Unlike right ascension, hour angle is always increasing with the rotation of Earth. Hour angle may be considered a means of measuring the time since upper culmination, the moment when an object contacts the meridian overhead.
A culminating star on the observer's meridian is said to have a zero hour angle (0h). One sidereal hour (approximately 0.9973 solar hours) later, Earth's rotation will carry the star to the west of the meridian, and its hour angle will be 1h. When calculating topocentric phenomena, right ascension may be converted into hour angle as an intermediate step.[8][9][10]
3. Rectangular Coordinates
3.1. Geocentric Equatorial Coordinates
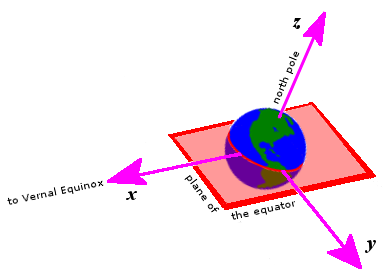
There are a number of rectangular variants of equatorial coordinates. All have:
- The origin at the centre of the Earth.
- The fundamental plane in the plane of the Earth's equator.
- The primary direction (the x axis) toward the vernal equinox, that is, the place where the Sun crosses the celestial equator in a northward direction in its annual apparent circuit around the ecliptic.
- A right-handed convention, specifying a y axis 90° to the east in the fundamental plane and a z axis along the north polar axis.
The reference frames do not rotate with the Earth (in contrast to Earth-centred, Earth-fixed frames), remaining always directed toward the equinox, and drifting over time with the motions of precession and nutation.
- In astronomy:[11]
- The position of the Sun is often specified in the geocentric equatorial rectangular coordinates X, Y, Z and a fourth distance coordinate, R (= √X2 + Y2 + Z2), in units of the astronomical unit.
- The positions of the planets and other Solar System bodies are often specified in the geocentric equatorial rectangular coordinates ξ, η, ζ and a fourth distance coordinate, Δ (equal to √ξ2 + η2 + ζ2), in units of the astronomical unit.
These rectangular coordinates are related to the corresponding spherical coordinates by
- [math]\displaystyle{ \begin{align} \frac{X}{R} = \frac{\xi}{\mathit{\Delta}} &= \cos \delta \cos \alpha \\ \frac{Y}{R} = \frac{\eta}{\mathit{\Delta}} &= \cos \delta \sin \alpha \\ \frac{Z}{R} = \frac{\zeta}{\mathit{\Delta}} &= \sin \delta \end{align} }[/math]
- In astrodynamics:[12]
- The positions of artificial Earth satellites are specified in geocentric equatorial coordinates, also known as geocentric equatorial inertial (GEI), Earth-centred inertial (ECI), and conventional inertial system (CIS), all of which are equivalent in definition to the astronomical geocentric equatorial rectangular frames, above. In the geocentric equatorial frame, the x, y and z axes are often designated I, J and K, respectively, or the frame's basis is specified by the unit vectors Î, Ĵ and K̂.
- The Geocentric Celestial Reference Frame (GCRF) is the geocentric equivalent of the International Celestial Reference Frame (ICRF). Its primary direction is the equinox of J2000.0, and does not move with precession and nutation, but it is otherwise equivalent to the above systems.
| Spherical | Rectangular | ||||
|---|---|---|---|---|---|
| Right ascension | Declination | Distance | General | Special-purpose | |
| Geocentric | α | δ | Δ | ξ, η, ζ | X, Y, Z (Sun) |
| Heliocentric | x, y, z | ||||
3.2. Heliocentric Equatorial Coordinates
In astronomy, there is also a heliocentric rectangular variant of equatorial coordinates, designated x, y, z, which has:
- The origin at the centre of the Sun.
- The fundamental plane in the plane of the Earth's equator.
- The primary direction (the x axis) toward the vernal equinox.
- A right-handed convention, specifying a y axis 90° to the east in the fundamental plane and a z axis along Earth's north polar axis.
This frame is in every way equivalent to the ξ, η, ζ frame, above, except that the origin is removed to the centre of the Sun. It is commonly used in planetary orbit calculation. The three astronomical rectangular coordinate systems are related by[14]
- [math]\displaystyle{ \begin{align} \xi &= x + X \\ \eta &= y + Y \\ \zeta &= z + Z \end{align} }[/math]
The content is sourced from: https://handwiki.org/wiki/Astronomy:Equatorial_coordinate_system
References
- Explanatory Supplement (1961), pp. 20, 28
- Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 137. ISBN 0-943396-35-2.
- Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 28–29. ISBN 0-521-35699-7. https://archive.org/details/practicalastrono0000duff/page/28.
- Meir H. Degani (1976). Astronomy Made Simple. Doubleday & Company, Inc. p. 216. ISBN 0-385-08854-X. https://archive.org/details/astronomymadesim00hamb.
- Astronomical Almanac 2010, p. M4
- Moulton, Forest Ray (1918). An Introduction to Astronomy. p. 127. https://books.google.com/books?id=PJoUAQAAMAAJ.
- Astronomical Almanac 2010, p. M14
- Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. pp. 34–36. ISBN 0-521-35699-7. https://archive.org/details/practicalastrono0000duff/page/34.
- Astronomical Almanac 2010, p. M8
- Vallado (2001), p. 154
- Explanatory Supplement (1961), pp. 24–26
- Vallado (2001), pp. 157, 158
- Explanatory Supplement (1961), sec. 1G
- Explanatory Supplement (1961), pp. 20, 27
