1. Blind Frequency-Resolved Optical Gating (Blind FROG) and Double Blind FROG

Early attempts to solve the two-pulse measurement problem were made by Trebino and Kane and co-workers beginning in 1995.^[1][2] They took advantage of the fact that FROG and its variations involved crossing two replicas of the pulse to be measured in a nonlinear-optical medium (where one gated the other in time) and measuring the spectrum of the product of the two pulse electric fields vs. delay. Thus, instead of using a known reference pulse as the gate, the second unknown pulse was used as the gate. The mathematical form of the measured trace is, [math]\displaystyle{ I(\omega ,\tau )=|\int e^{ -i\omega t }E_{ 1 }(t)|E_{ 2 }(t-\tau )|^{ 2 }dt|^{ 2 } }[/math]. This particular experimental setup has come to be known as Blind FROG due to its mathematical equivalence to Blind Deconvolution.
Unfortunately, retrieval of two pulses from the Blind FROG trace proved to be ill-posed; many different pulse pairs yield the same measured trace. Without extra information about the pulses, such as the spectra, non-trivial ambiguities are found by the Blind FROG retrieval algorithm.^[3] However, even with the spectra, algorithm convergence was found to be too slow.
The attosecond-laser-pulse community, however, finds the Blind FROG approach useful due to the specific mathematical form used in the retrieval algorithm in this case. On the other hand, for more common, longer pulses, improvements were required.
File:Blind FROG setup.tif In 2002, in his book,^[4] Trebino proposed “Double Blind FROG” (DB FROG) to solve the two-pulse measurement problem. DB FROG is a slightly modified version of Blind FROG in which two FROG traces are measured. This second FROG trace contains the extra information required to retrieve both pulses essentially uniquely (with only trivial ambiguities, such as the zeroth-order phase and the first-order spectral phase, which corresponds to the pulses’ average arrival time).
To understand DB FROG, it helps to consider a particular FROG beam geometry. Here we consider the polarization-gate (PG) geometry. The modification required to turn a Blind PG FROG into Double Blind PG FROG is the addition of a pair of crossed polarizers and a spectrometer. The main idea behind DB FROG is that, when one pulse gates the other, the other must also gate the one. In Blind FROG (see Blind FROG schematic), the gated pulse 2 is simply dumped after the nonlinear medium. But in DB PG FROG (see Figure 2), it passes through a crossed polarizer and is spectrally resolved to generate a second FROG trace. In DB PG FROG, trace 1 is proportional to [math]\displaystyle{ |\int e^{ -i\omega t }E_{ 1 }(t)|E_{ 2 }(t-\tau )|^{ 2 }dt|^{ 2 } }[/math] where [math]\displaystyle{ E_{1} }[/math] and [math]\displaystyle{ E_{2} }[/math] are the two light pulse electric fields. This expression is identical to that in PG XFROG. Trace 2 is proportional to [math]\displaystyle{ |\int e^{ -i\omega t }E_{ 2 }(t)|E_{ 1 }(t-\tau )|^{ 2 }dt|^{ 2 } }[/math] where the roles of the two pulses are reversed. This term, of course, also has the form of a FROG trace produced by PG XFROG. The DB FROG retrieval algorithm uses information contained in both traces to retrieve both of the unknown pulses. File:Double Blind FROG Schematic.tif

2. Retrieval Algorithm

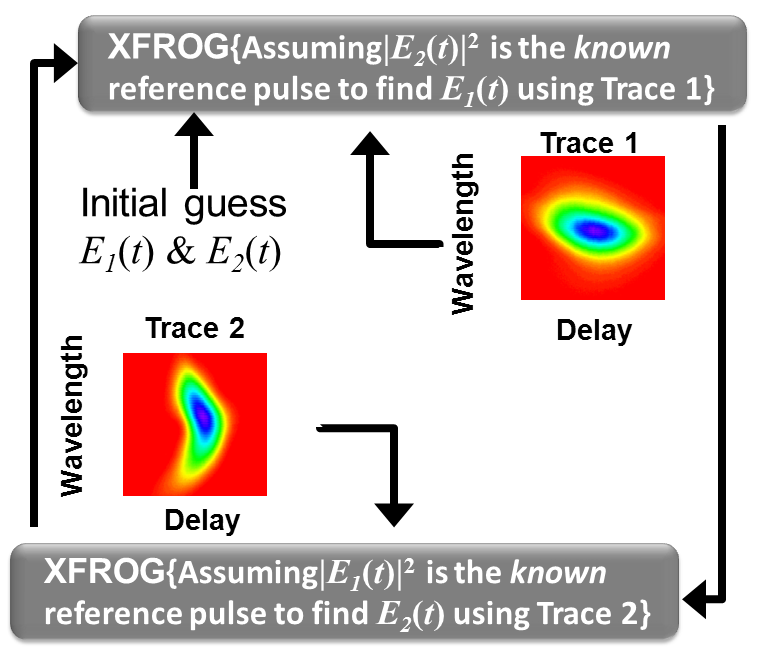
A unique DB FROG retrieval algorithm, based on the XFROG algorithm, is used to retrieve the two unknown pulses by making use of the two recorded traces. The retrieval algorithm divides the whole retrieval problem into two XFROG problems. It starts with random initial guesses for both unknown pulses and takes one of the unknown two pulses, say, [math]\displaystyle{ E_{1} }[/math] as the unknown and [math]\displaystyle{ E_{2} }[/math] as the gate. Even though [math]\displaystyle{ E_{2} }[/math] is not the correct gate pulse to begin with, the algorithm treats it as if it is the correct one. The standard XFROG algorithm along with trace 1 is used to retrieve [math]\displaystyle{ E_{1} }[/math]. The returned [math]\displaystyle{ E_{1} }[/math] is not the correct one, but it is an improved version of it, since trace 1 contains information about [math]\displaystyle{ E_{1} }[/math]. This improved version of [math]\displaystyle{ E_{1} }[/math] is then used in the next step of the retrieval algorithm, which now reverses the roles of [math]\displaystyle{ E_{1} }[/math] and [math]\displaystyle{ E_{2} }[/math] ([math]\displaystyle{ E_{1} }[/math] as known and [math]\displaystyle{ E_{2} }[/math] as the unknown) and runs trace 2 with standard XFROG algorithm to produce a better version of [math]\displaystyle{ E_{2} }[/math]. This completes one cycle of the retrieval algorithm and improves both [math]\displaystyle{ E_{1} }[/math] and [math]\displaystyle{ E_{2} }[/math]. The retrieval algorithm then uses the improved results for [math]\displaystyle{ E_{1} }[/math] and [math]\displaystyle{ E_{2} }[/math] to perform the next cycle. It continues alternating between traces 1 and 2 until the desired agreement between measured and retrieved traces occurs. It typically takes 3-5 cycles to converge depending on the complexity of the pulse pair. Also, complete convergence on early iterations is not necessary.

Retrieval algorithm flow chart for DB PG FROG. https://handwiki.org/wiki/index.php?curid=1526074

3. Experimental and Numerical Results

Pulse pairs with Time Bandwidth Products (TBP) ranging from 1 to 6 and also different wavelengths have been measured and retrieved experimentally using DB PG FROG.^[5][6] These measurements demonstrated that the DB FROG retrieval algorithm is capable of ignoring experimental noise and various inevitable non-physical details in the recorded traces and that it returns the correct retrieved pulse.
In addition to experimental work, numerical simulations have also shown that the DB FROG retrieval algorithm is extremely robust and reliable.

4. Advantages and Disadvantages

Depending on the gating geometry of the experimental setup, DB FROG inherits both advantages and disadvantages from the particular geometry. In the case of Polarization-Gate geometry, the advantage is the infinite phase-matching bandwidth which makes the system alignment insensitive. On the other hand, a disadvantage of PG geometry is the requirement of high-quality polarizers (calcite polarizers work fine) which could be expensive and introduce non-negligible distortion into the pulse. This distortion could be removed by numerically back propagating the pulse through the polarizer. DB FROG is promising and, although not in widespread use, it is a subject of active current research.

The content is sourced from: https://handwiki.org/wiki/Physics:Double-Blind_FROG