Subjective expected relative similarity (SERS) is a normative and descriptive theory that predicts and explains cooperation levels in a family of games termed Similarity Sensitive Games (SSG), among them the well-known Prisoner's Dilemma game (PD). SERS was originally developed in order to (i) provide a new rational solution to the PD game and (ii) to predict human behavior in single-step PD games. It was further developed to account for: (i) repeated PD games, (ii) evolutionary perspectives and, as mentioned above, (iii) the SSG subgroup of 2x2 games. SERS predicts that individuals cooperate whenever their subjectively perceived similarity with their opponent exceeds a situational index derived from the game’s payoffs, termed the similarity threshold of the game. SERS proposes a solution to the rational paradox associated with the single step PD and provides accurate behavioral predictions. The theory was developed by Prof. Ilan Fischer at the University of Haifa.
- rational solution
- perceived similarity
- similarity
1. The Prisoner's Dilemma
Script error: No such module "in5".The dilemma is described by a 2 x 2 payoff matrix that allows each player to choose between a cooperative and a competitive (or defective) move. If both players cooperate, each player obtains the reward (R) payoff. If both defect, each player obtains the punishment (P) payoff. However, if one player defects while the other cooperates, the defector obtains the temptation (T) payoff and the cooperator obtains the sucker’s (S) payoff, where
T > R > P > S (and, R ≥ T+S/2 assuring that sharing the payoffs awarded for uncoordinated choices does not exceed the payoffs obtained by mutual cooperation).
Given the payoff structure of the game (see Table 1), each individual player has a dominant strategy of defection. This dominant strategy yields a better payoff regardless of the opponent’s choice. By choosing to defect, players protect themselves from exploitation and retain the option to exploit a trusting opponent. Because this is the case for both players, mutual defection is the only Nash equilibrium of the game. However, this is a deficient equilibrium (since mutual cooperation results in a better payoff for both players).[1]
The PD game payoff matrix:
| Player 2 cooperates | Player 2 defects | |
|---|---|---|
| Player 1 cooperates | R, R | S, T |
| Player 1 defects | T, S | P, P |
Table 1:Payoffs are denoted as temptation (T), reward (R), punishment (P) and sucker (S)
1.1. The Repeated Prisoner's Dilemma Game
Players that knowingly interact for several games (where the end point of the game is unknown), thus playing a repeated Prisoner's Dilemma game, may still be motivated to cooperate with their opponent while attempting to maximise their payoffs along the entire set of their repeated games. Such Players face a different challenge of choosing an efficient and lucrative strategy for the repeated play. This challenge may become more complex when individuals are embedded in an ecology, having to face many opponents with various and unknown strategies.[2][3][4]
2. The SERS Theory
Script error: No such module "in5".SERS assumes that the similarity between the players is subjectively and individually perceived (denoted as ps, where 0 ≤ ps ≤ 1). Two players confronting each other may have either identical or different perceptions of their similarity to their opponent. In other words, similarity perceptions need neither be symmetric nor correspond to formal logic constraints. After perceiving ps, each player chooses between cooperation and defection, attempting to maximize the expected outcome. This means that each player estimates his or her expected payoffs under each of two possible courses of action. The expected value of cooperation is given by
R × ps + S × (1-ps) and the expected payoff of defection is given by P x ps + T x (1 - ps). Hence, cooperation provides a higher expected payoff whenever
R x ps + S x (1 - ps) > P x ps + T x (1 - ps) which may also be expressed further as:
Script error: No such module "in5". Cooperate if ps>T-S/T-S+R-P. Defining ps*=T-S/T-S+R-P, we obtain a simple decision rule: cooperate whenever ps > ps*, where ps denotes the level of perceived similarity with the opponent, and Ps* denotes the similarity threshold derived from the payoff matrix.
 Fig. 1: The SERS Decision Tree for single step PD games. The expected value of cooperation is given by
Fig. 1: The SERS Decision Tree for single step PD games. The expected value of cooperation is given by R × ps + S × (1-ps), the expected value for defection is given by P x ps + T x (1 - ps). Thus cooperation should be preferred over defection whenever R x ps + S x (1 - ps) > P x ps + T x (1 - ps), or when ps > ps* . https://handwiki.org/wiki/index.php?curid=1697129
To illustrate, consider a PD payoff matrix with T = 5, R = 3, P = 1, S = 0. The similarity threshold calculated for the game is given by:
ps*= 5 - 0/5 - 0 + 3 - 1 ≈ 0.71. Thus a player perceiving the similarity with the opponent, ps, exceeding 0.71 should cooperate in order to maximise his expected payoffs.
2.1. Empirical Evidence
Several experiments were conducted to test whether SERS provides not only a normative theory but also a descriptive theory of human behaviour.
For example, an experiment involving 215 university undergraduates revealed an average of 30% cooperation rate for a payoff matrix with ps* = 0.8 and an average of 46% cooperation rate for a payoff matrix ps* = 0.63. Participants cooperated 47% under high level of induced similarity and only 29% under low level of induced similarity. The cooperation rate for manipulating the perception of similarity of the opponent, revealed an increase from 67% to 80% of cooperation for the lower similarity threshold and from 40% to 70% cooperation for the higher similarity threshold.
Other experiments with various similarity induction methods and payoff matrices further confirmed SERS's status as a descriptive theory of human behaviour.[5] [1]
| Similarity (ps) | ||||
|---|---|---|---|---|
| Low Similarity | High Similarity | Marginal Mean | ||
| Similarity Threshold | Low ps*= 0.63 | 33% | 59% | 46% |
| High ps* = 0.8 | 25% | 34% | 30% | |
| Marginal Mean | 29% | 47% | ||
Table 2:Level of cooperation for two similarity threshold and two levels of similarity
2.2. The SERS Theory for Repeated PD Games
Experiments on the impact of SERS on repeated games are presently being conducted and analysed at the University of Haifa and the Max Planck Institute for Research on Collective Goods in Bonn.
2.3. Similarity Sensitive Games
The PD game is not the only similarity sensitive game. Games for which the choice of the action with the higher expected value depends on the value of ps are defined as Similarity Sensitive Games (SSGs), whereas others are nonsimilarity sensitive. Focusing only on the 24 completely rank-ordered and symmetric games, we can mark 12 SSGs. After eliminating games that reflect permutations of other games generated either by switching rows, columns, or both rows and columns, we are left with six basic (completely rank-ordered and symmetric) SSGs. These are games for which SERS provides a rational and payoff-maximizing strategy that recommends which alternative to choose for any given perception of similarity with the opponent[5]
3. Mimicry and Relative Similarity (MaRS)
Developing the SERS theory into an evolutionary strategy yields the Mimicry and Relative Similarity (MaRS) algorithm. Fusing enacted and expected mimicry generates a powerful and cooperative mechanism that enhances fitness and reduces the risks associated with trust and cooperation. When conflicts take the form of repeated PD games, individuals get the opportunity to learn and monitor the extent of similarity with their opponents. They can then react by choosing whether to enact, expect, or exclude mimicry. This rather simple behavior has the capacity to protect individuals from exploitation and drive the evolution of cooperation within entire populations. MaRS paves the way for the induction of cooperation and supports the survival of other cooperative strategies. The existence of MaRS in heterogeneous populations helps those cooperative strategies that do not have the capacity of MaRS to combat hostile and random opponents. Despite the fact that MaRS cannot prevail in a duel with an unconditional defector, interacting within heterogeneous populations allows MaRS to fight unpredictable and hostile strategies and cooperate with cooperative ones, including itself. The operation of MaRS promotes cooperation, minimizes the extent of exploitation, and accounts for high fitness levels. Testing the model in computer simulations of behavioral niches, populated with agents that enact various strategies and learning algorithms, shows how mimicry and relative similarity outperforms all the opponent strategies it was tested against, pushes noncooperative opponents toward extinction, and promotes the development of cooperative populations.[6]
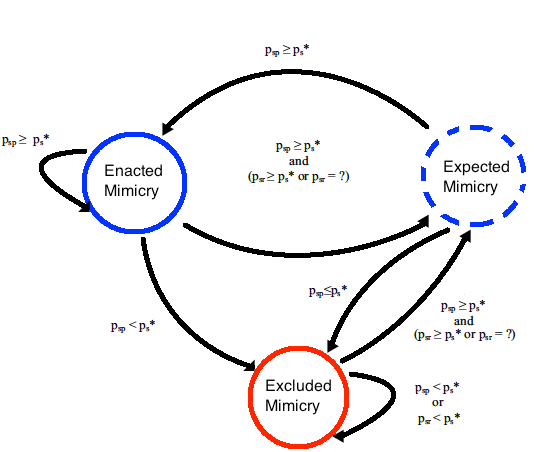 Fig. 2: The transition of MaRS among three mimicry modes: enacted, expected, and excluded. Each transition is conditioned upon the detection of up-to-date similarity levels by the passive similarity index psp, the reactive similarity index psr, or both. The criterion for sufficient similarity is the similarity threshold ps* defined by SERS. https://handwiki.org/wiki/index.php?curid=1826232
Fig. 2: The transition of MaRS among three mimicry modes: enacted, expected, and excluded. Each transition is conditioned upon the detection of up-to-date similarity levels by the passive similarity index psp, the reactive similarity index psr, or both. The criterion for sufficient similarity is the similarity threshold ps* defined by SERS. https://handwiki.org/wiki/index.php?curid=1826232The content is sourced from: https://handwiki.org/wiki/Subjective_expected_relative_similarity_(SERS)
References
- Fischer, I. (2009). Friend or foe: subjective expected relative similarity as a determinant of cooperation. Journal of Experimental Psychology: General, 138(3), 341.
- Axelrod, R., & Hamilton, W. D. (1981). The evolution of cooperation. Science, 211(4489), 1390-1396.
- Axelrod, Robert (1984), The Evolution of Cooperation, Basic Books, ISBN:0-465-02122-0
- Nowak, M., & Sigmund, K. (1993). A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner's Dilemma game. Nature, 364(6432), 56-58.
- Fischer, I. (2012). Similarity or reciprocity? On the determinants of cooperation in similarity-sensitive games. Psychological Inquiry, 23(1), 48-54.
- Fischer, I., Frid, A., Goerg, S. J., Levin, S. A., Rubenstein, D. I., & Selten, R. (2013). Fusing enacted and expected mimicry generates a winning strategy that promotes the evolution of cooperation. Proceedings of the National Academy of Sciences, 110(25), 10229-10233.
