Numerical models can be used for many purposes in oil and gas engineering, such as production optimization and forecasting, uncertainty analysis, history matching, and risk assessment. However, subsurface problems are complex and non-linear, and making reliable decisions in reservoir management requires substantial computational effort. Proxy models have gained much attention in recent years. They are advanced non-linear interpolation tables that can approximate complex models and alleviate computational effort. Proxy models are constructed by running high-fidelity models to gather the necessary data to create the proxy model. Once constructed, they can be a great choice for different tasks such as uncertainty analysis, optimization, forecasting, etc. The application of proxy modeling in oil and gas has had an increasing trend in recent years, and there is no consensus rule on the correct choice of proxy model. As a result, it is crucial to better understand the advantages and disadvantages of various proxy models.
- proxy model
- surrogate model
- traditional proxy
- smart proxy
- multi-fidelity
- reduced-order
- sensitivity analysis
- sampling
- machine learning
- application
1. Introduction
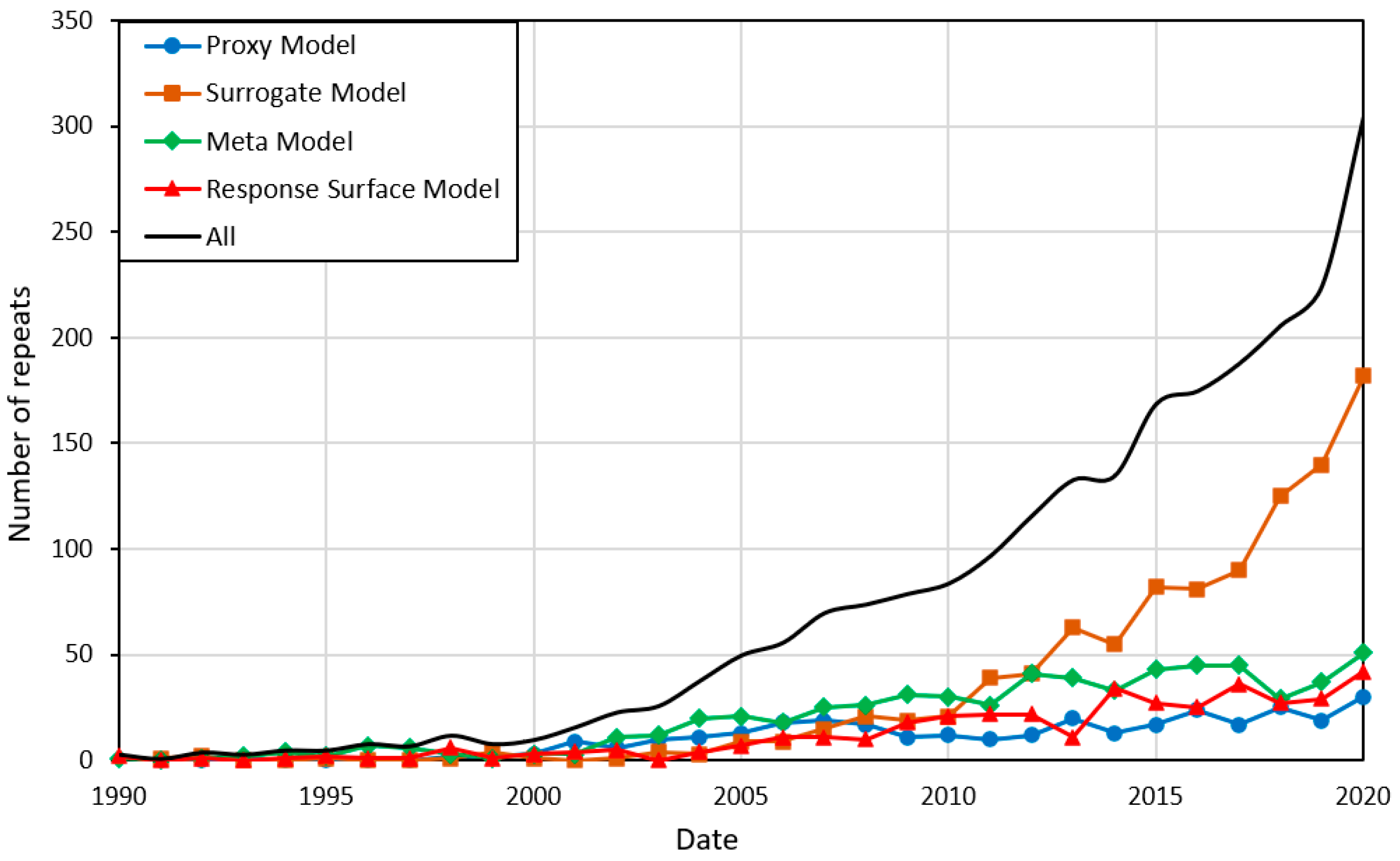
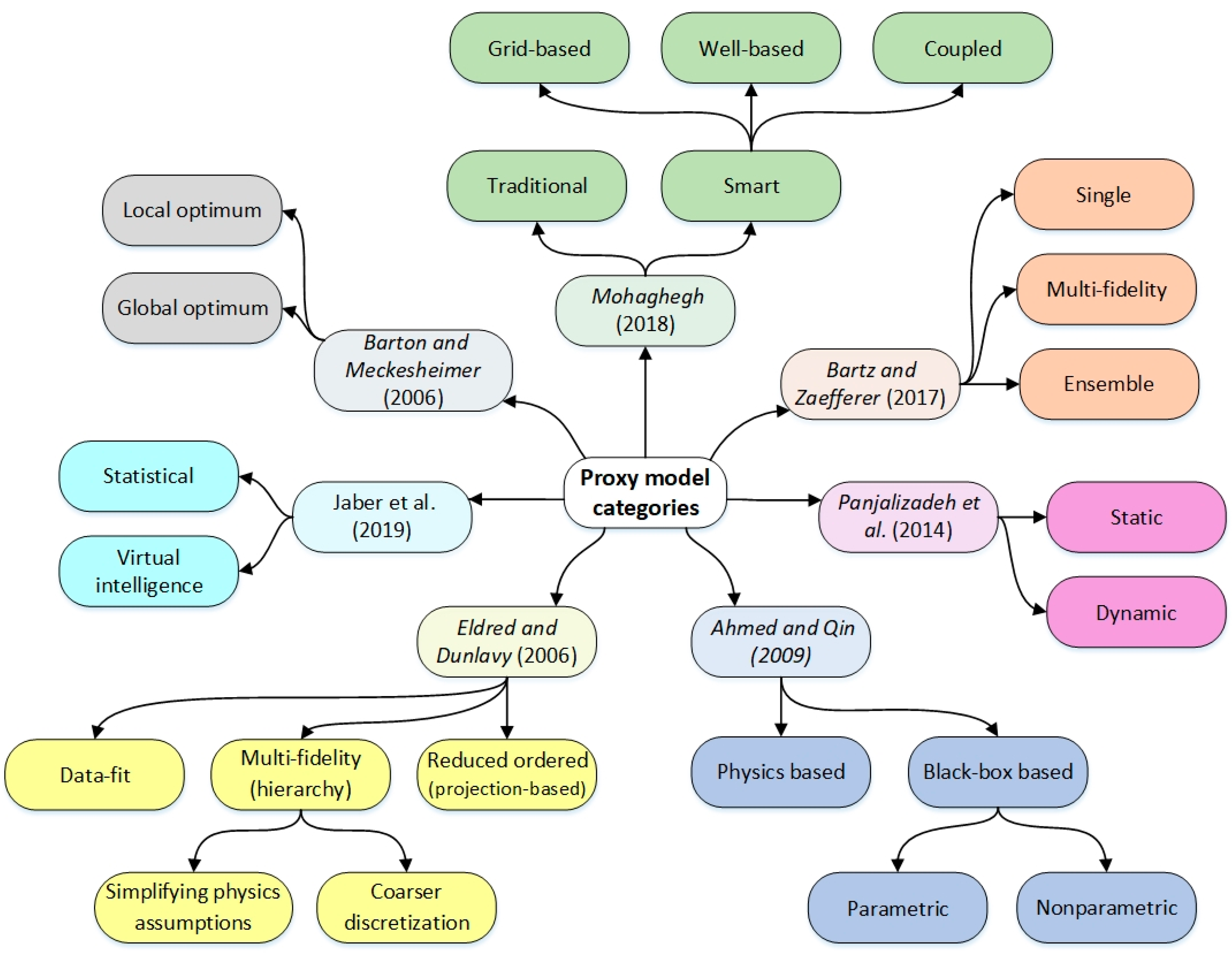
2. Proxy Modeling Classification
3. Application of Proxy Models in the Oil and Gas Industry
3.1. Multi-Fidelity Models (MFM)
3.2. Reduced-Order Models (ROM)
3.3. Traditional Proxy Models (TPM)
3.4. Smart Proxy Models (SPM)
4. Conclusions
This entry is adapted from the peer-reviewed paper 10.3390/en15145247
References
- Larson, M. Numerical Modeling. In Encyclopedia of Coastal Science; Schwartz, M.L., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 730–733. ISBN 978-1-4020-3880-8.
- Carmo, J.S.A.d. Physical Modelling vs. Numerical Modelling: Complementarity and Learning. Preprints 2020.
- Ferziger, J.H.; Perić, M. Introduction to Numerical Methods. In Computational Methods for Fluid Dynamics; Ferziger, J.H., Perić, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 21–37. ISBN 978-3-642-56026-2.
- Koziel, S.; Leifsson, L. Surrogate-Based Modeling and Optimization: Applications in Engineering; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7550-7.
- Avansi, G.; Rios, V.; Schiozer, D. Numerical Tuning in Reservoir Simulation: It Is Worth the Effort in Practical Petroleum Applications. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 59.
- Available online: http://www.webofknowledge.com/ (accessed on 14 August 2021).
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; ISBN 978-0-470-77080-1.
- Ahmed, M.; Qin, N. Surrogate-Based Aerodynamic Design Optimization: Use of Surrogates in Aerodynamic Design Optimization. In Proceedings of the International Conference on Aerospace Sciences and Aviation Technology, Cairo, Egypt, 9–11 April 2009; Volume 13, pp. 1–26.
- Eldred, M.; Dunlavy, D. Formulations for Surrogate-Based Optimization with Data Fit, Multifidelity, and Reduced-Order Models. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006.
- Panjalizadeh, H.; Alizadeh, N.; Mashhadi, H. A Workflow for Risk Analysis and Optimization of Steam Flooding Scenario Using Static and Dynamic Proxy Models. J. Pet. Sci. Eng. 2014, 121, 78–86.
- Mohaghegh, S.D. Data-Driven Analytics for the Geological Storage of CO2; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018; ISBN 978-1-315-28081-3.
- Bartz-Beielstein, T.; Zaefferer, M. Model-Based Methods for Continuous and Discrete Global Optimization. Appl. Soft Comput. 2017, 55, 154–167.
- Barton, R.R.; Meckesheimer, M. Chapter 18—Metamodel-Based Simulation Optimization. In Handbooks in Operations Research and Management Science; Henderson, S.G., Nelson, B.L., Eds.; Simulation; Elsevier: Amsterdam, The Netherlands, 2006; Volume 13, pp. 535–574.
- Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A Review of Proxy Modeling Applications in Numerical Reservoir Simulation. Arab. J. Geosci. 2019, 12, 701.
- Batycky, R.P.; Blunt, M.J.; Thiele, M.R. A 3D Field-Scale Streamline-Based Reservoir Simulator. SPE Reserv. Eng. 1997, 12, 246–254.
- Tanaka, S.; Onishi, T.; Kam, D.; Dehghani, K.; Wen, X.-H. Application of Combined Streamline Based Reduced-Physics Surrogate and Response Surface Method for Field Development Optimization; OnePetro: Dhahran, Saudi Arabia, 2020.
- Thiele, M.R.; Batycky, R.P. Water Injection Optimization Using a Streamline-Based Workflow; OnePetro: Denver, CO, USA, 2003.
- Kovscek, A.R.; Wang, Y. Geologic Storage of Carbon Dioxide and Enhanced Oil Recovery. I. Uncertainty Quantification Employing a Streamline Based Proxy for Reservoir Flow Simulation. Energy Convers. Manag. 2005, 46, 1920–1940.
- Wang, Y.; Kovscek, A.R. Streamline Approach for History Matching Production Data. SPE J. 2000, 5, 353–362.
- Stenerud, V.R.; Kippe, V.; Lie, K.-A.; Datta-Gupta, A. Adaptive Multiscale Streamline Simulation and Inversion for High-Resolution Geomodels. SPE J. 2008, 13, 99–111.
- Kam, D.; Han, J.; Datta-Gupta, A. Streamline-Based History Matching of Bottomhole Pressure and Three-Phase Production Data Using a Multiscale Approach. J. Pet. Sci. Eng. 2017, 154, 217–233.
- Milliken, W.J.; Emanuel, A.S.; Chakravarty, A. Applications of 3D Streamline Simulation to Assist History Matching. SPE Reserv. Eval. Eng. 2001, 4, 502–508.
- Taware, S.; Park, H.-Y.; Datta-Gupta, A.; Bhattacharya, S.; Tomar, A.K.; Kumar, M.; Rao, H.S. Well Placement Optimization in a Mature Carbonate Waterflood Using Streamline-Based Quality Maps; OnePetro: Mumbai, India, 2012.
- Thiele, M.R.; Batycky, R.P.; Blunt, M.J.; Orr, F.M., Jr. Simulating Flow in Heterogeneous Systems Using Streamtubes and Streamlines. SPE Reserv. Eng. 1996, 11, 5–12.
- Datta-Gupta, A.; King, M.J. Streamline Simulation: Theory and Practice; Society of Petroleum Engineers: London, UK, 2007; ISBN 978-1-55563-111-6.
- Bardy, G.; Biver, P.; Caumon, G.; Renard, P. Oil Production Uncertainty Assessment by Predicting Reservoir Production Curves and Confidence Intervals from Arbitrary Proxy Responses. J. Pet. Sci. Eng. 2019, 176, 116–125.
- Allam, F.A.; El-Banbi, A.H.; Bustami, S.S.; Saada, T.H.; Fahmy, I.I. History Match Tuning through Different Upscaling Algorithms; OnePetro: Houston, TX, USA, 2004.
- Li, H.; Durlofsky, L.J. Upscaling for Compositional Reservoir Simulation. SPE J. 2016, 21, 0873–0887.
- Yang, Y.; Wang, X.; Wu, X.-H.; Bi, L. Multiphase Upscaling Using Approximation Techniques; OnePetro: The Woodlands, TX, USA, 2013.
- Rios, V.S.; Santos, L.O.S.; Quadros, F.B.; Schiozer, D.J. New Upscaling Technique for Compositional Reservoir Simulations of Miscible Gas Injection. J. Pet. Sci. Eng. 2019, 175, 389–406.
- Bruce, W.A. An Electrical Device for Analyzing Oil-Reservoir Behavior. Trans. AIME 1943, 151, 112–124.
- Yousef, A.A.; Gentil, P.H.; Jensen, J.L.; Lake, L.W. A Capacitance Model to Infer Interwell Connectivity from Production and Injection Rate Fluctuations. SPE Reserv. Eval. Eng. 2006, 9, 630–646.
- Almarri, M.; Prakasa, B.; Muradov, K.; Davies, D. Identification and Characterization of Thermally Induced Fractures Using Modern Analytical Techniques; OnePetro: Dammam, Saudi Arabia, 2017.
- Chatterjee, A. An Introduction to the Proper Orthogonal Decomposition. Curr. Sci. 2000, 78, 808–817.
- Markovinović, R.; Jansen, J.D. Accelerating Iterative Solution Methods Using Reduced-Order Models as Solution Predictors. Int. J. Numer. Methods Eng. 2006, 68, 525–541.
- Cardoso, M.A.; Durlofsky, L.J.; Sarma, P. Development and Application of Reduced-Order Modeling Procedures for Subsurface Flow Simulation. Int. J. Numer. Methods Eng. 2009, 77, 1322–1350.
- van Doren, J.F.M.; Markovinović, R.; Jansen, J.-D. Reduced-Order Optimal Control of Water Flooding Using Proper Orthogonal Decomposition. Comput. Geosci. 2006, 10, 137–158.
- Sun, X.; Xu, M. Optimal Control of Water Flooding Reservoir Using Proper Orthogonal Decomposition. J. Comput. Appl. Math. 2017, 320, 120–137.
- Kaleta, M.P.; Hanea, R.G.; Heemink, A.W.; Jansen, J.-D. Model-Reduced Gradient-Based History Matching. Comput Geosci 2011, 15, 135–153.
- Cardoso, M.A.A.; Durlofsky, L.J.J. Use of Reduced-Order Modeling Procedures for Production Optimization. SPE J. 2009, 15, 426–435.
- Cardoso, M.A. Reduced-Order Models for Reservoir Simulation; OnePetro: New Orleans, LA, USA, 2009.
- Xiao, C.; Leeuwenburgh, O.; Lin, H.X.; Heemink, A. Non-Intrusive Subdomain POD-TPWL for Reservoir History Matching. Comput. Geosci. 2019, 23, 537–565.
- He, J.; Sarma, P.; Durlofsky, L.J. Reduced-Order Flow Modeling and Geological Parameterization for Ensemble-Based Data Assimilation. Comput. Geosci. 2013, 55, 54–69.
- Rousset, M.A.H.; Huang, C.K.; Klie, H.; Durlofsky, L.J. Reduced-Order Modeling for Thermal Recovery Processes. Comput. Geosci. 2014, 18, 401–415.
- He, J.; Durlofsky, L.J. Reduced-Order Modeling for Compositional Simulation Using Trajectory Piecewise Linearization; OnePetro: The Woodlands, TX, USA, 2013.
- Gildin, E.; Ghasemi, M.; Romanovskay, A.; Efendiev, Y. Nonlinear Complexity Reduction for Fast Simulation of Flow in Heterogeneous Porous Media; OnePetro: The Woodlands, TX, USA, 2013.
- Klie, H. Unlocking Fast Reservoir Predictions via Non-Intrusive Reduced Order Models; OnePetro: The Woodlands, TX, USA, 2013.
- Li, J.; Fan, X.; Wang, Y.; Yu, B.; Sun, S.; Sun, D. A POD-DEIM Reduced Model for Compressible Gas Reservoir Flow Based on the Peng-Robinson Equation of State. J. Nat. Gas Sci. Eng. 2020, 79, 103367.
- Ghommem, M.; Gildin, E.; Ghasemi, M. Complexity Reduction of Multiphase Flows in Heterogeneous Porous Media. SPE J. 2016, 21, 144–151.
- Alghareeb, Z.M.; Williams, J.R. Optimum Decision-Making in Reservoir Managment Using Reduced-Order Models; OnePetro: New Orleans, LA, USA, 2013.
- Al-Mudhafar, W.J. Polynomial and Nonparametric Regressions for Efficient Predictive Proxy Metamodeling: Application through the CO2-EOR in Shale Oil Reservoirs. J. Nat. Gas Sci. Eng. 2019, 72, 103038.
- Golzari, A.; Haghighat Sefat, M.; Jamshidi, S. Development of an Adaptive Surrogate Model for Production Optimization. J. Pet. Sci. Eng. 2015, 133, 677–688.
- Amiri Kolajoobi, R.; Haddadpour, H.; Emami Niri, M. Investigating the Capability of Data-Driven Proxy Models as Solution for Reservoir Geological Uncertainty Quantification. J. Pet. Sci. Eng. 2021, 205, 108860.
- Peng, C.Y.; Gupta, R. Experimental Design in Deterministic Modelling: Assessing Significant Uncertainties; OnePetro: Jakarta, Indonesia, 2003.
- Zubarev, D.I. Pros and Cons of Applying Proxy-Models as a Substitute for Full Reservoir Simulations; OnePetro: New Orleans, LA, USA, 2009.
- Guo, Z.; Chen, C.; Gao, G.; Vink, J. Applying Support Vector Regression to Reduce the Effect of Numerical Noise and Enhance the Performance of History Matching; OnePetro: San Antonio, TX, USA, 2017.
- Avansi, G.D. Use of Proxy Models in the Selection of Production Strategy and Economic Evaluation of Petroleum Fields; OnePetro: New Orleans, LA, USA, 4 October 2009.
- Ligero, E.L.; Madeira, M.G.; Schiozer, D.J. Comparison of Techniques for Risk Analysis Applied to Petroleum-Field Development; OnePetro: Rio de Janeiro, Brazil, 2005.
- Risso, F.V.A.; Risso, F.F.; Schiozer, D.J. Risk Assessment of Oil Fields Using Proxy Models: A Case Study. J. Can. Pet. Technol. 2008, 47, 9–14.
- Ebrahimi, A.; Khamehchi, E. Developing a Novel Workflow for Natural Gas Lift Optimization Using Advanced Support Vector Machine. J. Nat. Gas Sci. Eng. 2016, 28, 626–638.
- Ghassemzadeh, S.; Charkhi, A.H. Optimization of Integrated Production System Using Advanced Proxy Based Models: A New Approach. J. Nat. Gas Sci. Eng. 2016, 35, 89–96.
- Zangl, G.; Giovannoli, M.; Stundner, M. Application of Artificial Intelligence in Gas Storage Management; OnePetro: Vienna, Austria, 2006.
- Artun, E.; Ertekin, T.; Watson, R.; Al-Wadhahi, M. Development of Universal Proxy Models for Screening and Optimization of Cyclic Pressure Pulsing in Naturally Fractured Reservoirs. J. Nat. Gas Sci. Eng. 2011, 3, 667–686.
- Sprunger, C.; Muther, T.; Syed, F.I.; Dahaghi, A.K.; Neghabhan, S. State of the Art Progress in Hydraulic Fracture Modeling Using AI/ML Techniques. Model. Earth Syst. Environ. 2022, 8, 1–13.
- Syed, F.I.; AlShamsi, A.; Dahaghi, A.K.; Neghabhan, S. Application of ML & AI to Model Petrophysical and Geomechanical Properties of Shale Reservoirs—A Systematic Literature Review. Petroleum 2022, 8, 158–166.
- Gu, J.; Liu, W.; Zhang, K.; Zhai, L.; Zhang, Y.; Chen, F. Reservoir Production Optimization Based on Surrograte Model and Differential Evolution Algorithm. J. Pet. Sci. Eng. 2021, 205, 108879.
- Chen, G.; Zhang, K.; Xue, X.; Zhang, L.; Yao, J.; Sun, H.; Fan, L.; Yang, Y. Surrogate-Assisted Evolutionary Algorithm with Dimensionality Reduction Method for Water Flooding Production Optimization. J. Pet. Sci. Eng. 2020, 185, 106633.
- Ogbeiwi, P.; Stephen, K.D.; Arinkoola, A.O. Robust Optimisation of Water Flooding Using an Experimental Design-Based Surrogate Model: A Case Study of a Niger-Delta Oil Reservoir. J. Pet. Sci. Eng. 2020, 195, 107824.
- Bruyelle, J.; Guérillot, D. Optimization of Waterflooding Strategy Using Artificial Neural Networks; OnePetro: Abu Dhabi, United Arab Emirates, 2019.
- Bruyelle, J.; Guérillot, D. Well Placement Optimization with an Artificial Intelligence Method Applied to Brugge Field; OnePetro: Dubai, United Arab Emirates, 2019.
- Hassani, H.; Sarkheil, H.; Foroud, T.; Karimpooli, S. A Proxy Modeling Approach to Optimization Horizontal Well Placement; OnePetro: San Francisco, CA, USA, 2011.
- Nwachukwu, A.; Jeong, H.; Pyrcz, M.; Lake, L.W. Fast Evaluation of Well Placements in Heterogeneous Reservoir Models Using Machine Learning. J. Pet. Sci. Eng. 2018, 163, 463–475.
- Aydin, H.; Akin, S.; Senturk, E. A Proxy Model for Determining Reservoir Pressure and Temperature for Geothermal Wells. Geothermics 2020, 88, 101916.
- Wang, L.; Li, Z.; Adenutsi, C.D.; Zhang, L.; Lai, F.; Wang, K. A Novel Multi-Objective Optimization Method for Well Control Parameters Based on PSO-LSSVR Proxy Model and NSGA-II Algorithm. J. Pet. Sci. Eng. 2021, 196, 107964.
- Fedutenko, E.; Yang, C.; Card, C.; Nghiem, L.X. Time-Dependent Proxy Modeling of SAGD Process; OnePetro: Calgary, AB, Canada, 11 June 2013.
- Al-Mudhafar, W.J.; Rao, D.N. Proxy-Based Metamodeling Optimization of the Gas-Assisted Gravity Drainage GAGD Process in Heterogeneous Sandstone Reservoirs; OnePetro: Bakersfield, CA, USA, 2017.
- Jaber, A.K.; Awang, M.B.; Lenn, C.P. Box-Behnken Design for Assessment Proxy Model of Miscible CO2-WAG in Heterogeneous Clastic Reservoir. J. Nat. Gas Sci. Eng. 2017, 40, 236–248.
- Agada, S.; Geiger, S.; Elsheikh, A.; Oladyshkin, S. Data-Driven Surrogates for Rapid Simulation and Optimization of WAG Injection in Fractured Carbonate Reservoirs. Pet. Geosci. 2017, 23, 270–283.
- Ibiam, E.; Geiger, S.; Demyanov, V.; Arnold, D. Optimization of Polymer Flooding in a Heterogeneous Reservoir Considering Geological and History Matching Uncertainties. SPE Reserv. Eval. Eng. 2021, 24, 19–36.
- Haghshenas, Y.; Emami Niri, M.; Amini, S.; Amiri Kolajoobi, R. Developing Grid-Based Smart Proxy Model to Evaluate Various Water Flooding Injection Scenarios. Pet. Sci. Technol. 2020, 38, 870–881.
- Alenezi, F.; Mohaghegh, S. A Data-Driven Smart Proxy Model for a Comprehensive Reservoir Simulation. In Proceedings of the 2016 4th Saudi International Conference on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, 6–9 November 2016; pp. 1–6.
- Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4, 126.
- Gholami, V.; Mohaghegh, S.D.; Maysami, M. Smart Proxy Modeling of SACROC CO2-EOR. Fluids 2019, 4, 85.
- He, Q.; Mohaghegh, S.D.; Liu, Z. Reservoir Simulation Using Smart Proxy in SACROC Unit—Case Study; OnePetro: Canton, OH, USA, 2016.
- Shahkarami, A.; Mohaghegh, S.D.; Gholami, V.; Haghighat, S.A. Artificial Intelligence (AI) Assisted History Matching; OnePetro: Denver, CO, USA, 2014.
