Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Eukaryotic cells contain membranes with various curvatures, from the near-plane plasma membrane to the highly curved membranes of organelles, vesicles, and membrane protrusions. These curvatures are generated and sustained by curvature-inducing proteins, peptides, and lipids, and describing these mechanisms is an important scientific challenge. In addition to that, some molecules can sense membrane curvature and thereby be trafficked to specific locations.
- molecular dynamics (MD)
- lipid membrane
- membrane curvature
- vesicle
1. Introduction
Membrane curvature plays a central role in cellular trafficking. This role is apparent in the formation of vesicles during endo- and exocytosis. Membrane curvature also plays a more direct role, since differences in curvature can target curvature-sensing lipids, peptides, and proteins to specific locations [1]. However, by which mechanisms does membrane curvature induce the sorting of these molecules? There is a broad variation of membrane curvatures in mammalian cells: from the plasma membrane, which is flat at the nanoscopic scale, to the highly curved surfaces of the endoplasmic reticulum, the Golgi apparatus, membrane protrusions [2], or organelles, such as endosomes and lysosomes (Figure 1). However, how is membrane curvature generated and maintained in the different cellular compartments?
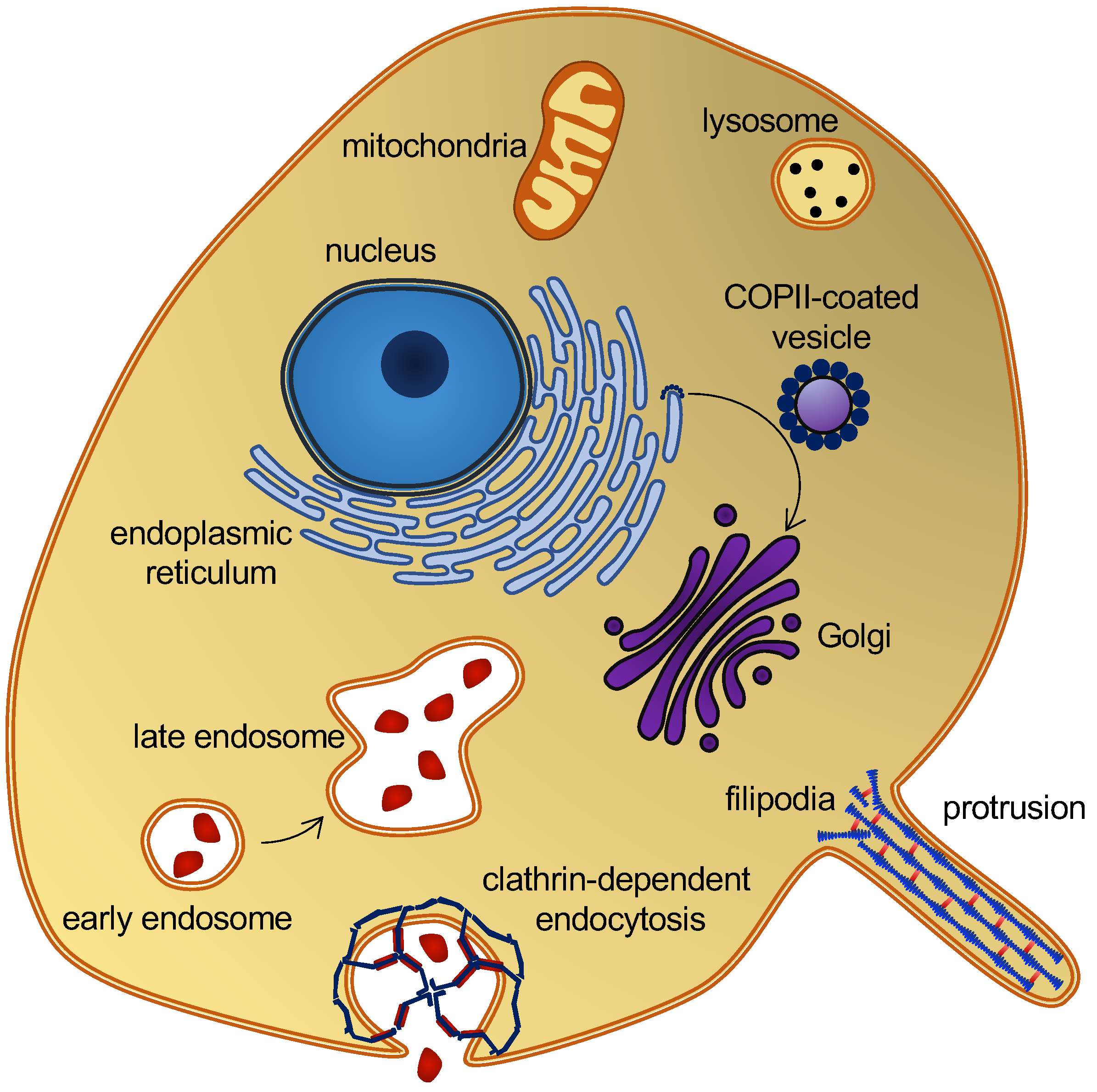
Figure 1. Eukaryotic cell and organelles, with examples of various membrane curvatures. Some curvature-inducing proteins are also shown, see the main text.
Molecular dynamics (MD) simulations provide molecular insight with high spatial and temporal resolution and MD is thus a strong complementary tool to experimental studies when addressing these questions. There are various methods for simulating curved lipid membranes with MD and, thanks to dedicated scientists, many of these are implemented, documented, and made available as open-source software. However, selecting the best method for a given problem is not trivial. One strategy is to model whole organelles [3][4]. Albeit attractive and promising, only short simulations have so far been made for whole organelles [5]. The focus is therefore on smaller model systems of curved membranes, with a more moderate computational cost, and the questions that may be unraveled by each model system are discussed. The researchers will not provide details about the levels of molecular resolution in different lipid models, as this has already been covered [6]. The entry is also limited to biological molecules, although nanotubes and nanoparticles can also induce and sense membrane curvatures [7][8], which is relevant, e.g., in bioengineering.
The motivation for writing the entry was thus to provide an overview of available tools for researchers who are interested in applying MD simulations to study the interplay between membrane curvature and proteins, peptides, and various lipid types. With the entry in hand, it should be easier to find the best-suited simulation approach for a given scientific question.
2. Biological Background
A variety of proteins and lipids induce membrane curvature or are sorted by membrane curvature. One group is the coating proteins COP I and COP II that mediate budding and vesicle transport between the endoplasmic reticulum and the Golgi apparatus [9], and the functionally related protein, clathrin, which also facilitates vesicle formation by coating [10] (Figure 1). The superfamily of BAR domain-containing proteins is another notable example. BAR domains form dimers whose shape resembles that of a banana or a crescent moon. They can scaffold the membrane into a curvature, defined by this shape, when nucleating on the membrane surface [11]. BAR domain-containing proteins can also create membrane curvatures by inserting amphipathic helices in a wedge-like mechanism, or by mere crowding [12][13][14]. BAR domains are involved in several membrane-reconstructing processes, including endocytosis and the formation of T-tubules, and they are thus key players in membrane remodeling. Another interesting curvature-dependent group is antimicrobial peptides. These peptides can penetrate and form pores in bacterial membranes, which make them a potential drug candidate that would constitute a much-needed alternative to conventional antibiotics [15]. Fusion peptides are another group of peptides that can penetrate and remodel lipid membranes. These peptides are part of fusion proteins, which are involved in viral entry and therefore constitute a potential target for anti-viral drugs [16]. Lipids themselves can also generate and sustain curvature. This can be achieved through lipid clustering and the formation of lipid rafts [17], or simply by an asymmetric lipid distribution in the inner and outer leaflets [18]. These are just a few examples that illustrate the abundance of membrane-curvature-inducing and curvature-sensing molecules. Other examples will be mentioned in the text, as the different methods for simulating membrane curvature are discussed.
3. Spontaneously Induced Membrane Curvature
An overview of methods that simulate how membrane curvature can be spontaneously induced by proteins, peptides, or lipids (i.e., without applying any virtual forces or scaffolding dummy beads) will be introduced here. The starting configuration is either randomly distributed lipids or a flat membrane, which is then reshaped into a curved membrane.
3.1. Self-Assembly
The least biased way to simulate spontaneous curvature is to allow the lipids (and proteins) to self-assemble from a randomly distributed initial configuration. This approach was used by Cooke and Deserno to investigate the role of the lipid packing parameter on membrane shape [19]. As simulated self-assembly is computationally expensive, the authors used an approximate force field with just three beads per lipid (i.e., around 50 atoms per bead) and implicit water. That is, the effect of water was introduced by an attractive force between beads representing the hydrophobic lipid tails.
Other methods, which will be discussed below, are computationally less expensive, enabling the use of force fields with higher resolution and explicit water. That level of resolution is necessary if molecular details rather than large-scale membrane changes are of interest. These methods use a preassembled lipid bilayer as the starting configuration.
3.2. Bending of Plane Bilayers with Periodic Boundary Conditions
A straight-forward strategy for monitoring spontaneously induced curvature is to simulate a flat membrane with periodic boundary conditions and probe the effect of adding curvature-inducing molecules, such as peripheral membrane proteins. This method has been applied in studies of, e.g., F-BAR domains [20] and N-BAR domains [21]. Some integral membrane proteins also induce spontaneous local curvature to obtain a better match between its transmembrane part and the hydrophobic core of a lipid bilayer [22]. The non-structural protein 4A of dengue virus is an example of a transmembrane protein that induces membrane curvature as a first step towards vesicle formation [23]. Intriguingly, MD simulations of a flat membrane have also been used to show that membrane curvature can be induced by mere protein crowding, i.e., by high concentrations of proteins, which have little or no affinity for lipid membranes by themselves [24] (Figure 2A).
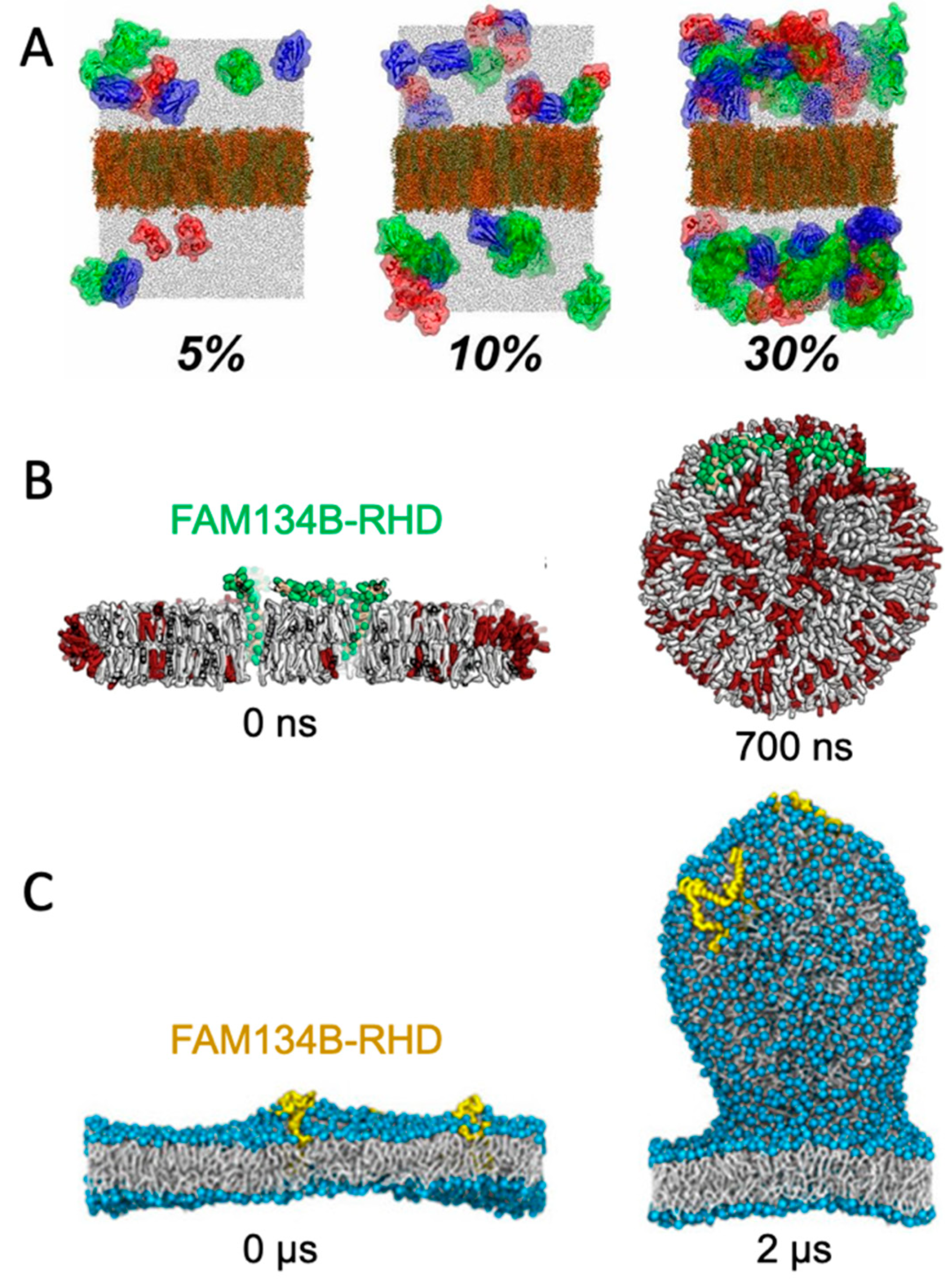
Figure 2. Simulating membrane curvature induction. (A) Bending of plane periodic bilayer by protein crowding. Figure adapted with permission from Ref. [24] (copyright 2019, PNAS license). (B) Bicelle to vesicle transition, adapted from Ref. [25]. (C) Tethering from a plane membrane, adapted from Ref. [26]. If not stated otherwise, the original figures are published under a creative common license.
A challenge for membrane curvature in planar membranes is the repulsive force from the periodic boundary condition, which inevitably leads to underestimation of the induced curvature. This is particularly critical for large perturbations of the curvature. The repulsive effect can, to some extent, be circumvented by simulating a larger membrane patch such that edge effects are negligible. However, smaller membranes are attractive due to lower computational costs, so methods have been developed to overcome the challenge of combining periodic boundary conditions with membrane curvature without making excessively large systems, as described in the following.
3.3. Bicelles and Bicelle-to-Vesicle Transitions
Small bilayer patches in solution are energetically unstable due to the exposed hydrophobic lipid tails at the rim. The bilayer patch can, however, be solubilized by detergents or short-tailed lipids to form bicelles, or by amphipathic helices or polymers to form nanodisc-like particles [27]. Bicelles are the most interesting of these systems in the context of membrane bending, as the flexible rim of detergents or short-tailed lipids allow the membrane to bend. Moreover, lipids can translocate from one leaflet to the other via the rim to equilibrate the density difference that inevitably builds up upon bending. Importantly, this pressure difference cannot be equilibrated in flat, periodic membranes, unless an artificial pore is formed and sustained. In that case, the artificial pore can be used by the lipids to translocate from the dense (concave) to the less dense (convex) leaflet. One example of the use of bicelles for studying membrane curvature is an MD-based investigation of curvature-inducing amyloid-β peptides [28]. In that study, the peptides bound to a metastable bicelle, allowing the bicelle to close in on itself and form a vesicle. In absence of the amyloid-β peptides, the energy barrier between bicelle and vesicle was too high for a spontaneous transformation to happen, but the peptides lowered the energy barrier. A similar approach was used to investigate the curvature-inducing properties of the reticulum homology domain (RHD) of ER-phagy receptor FAM134B [25] (Figure 2B). The clustering of protein on the bicelle led to a bicelle-to-vesicle transition. Simulations of bicelle-to-vesicle transitions have also been used to investigate the curvature induction of protein complexes from dengue virus [29].
3.4. Budding of Plane Membranes
The curvature-inducing properties of FAM134B-RHD were, in a later study, investigated by a different approach, using a plane membrane with a periodic boundary condition as the initial configuration [26]. The membranes had an imbalance between the number of lipids in the upper and lower leaflet, and was thereby in a metastable initial state, with a budded membrane constituting a more stable state. That is similar to the bicelle-to-vesicle transition which was also in a metastable state, but in the case of the bicelles, the initial plane membrane was instead unstable due to the exposed hydrophobic edges. FAM134B-RHD induced budding of the membrane by lowering the energy barrier between the plane membrane and the energetically favorable budded membrane state (Figure 2C). The budding approach allows for protrusions of different sizes [26], in contrast to the bicelle-to-vesicle transition method, where the final vesicle diameter is constrained by the number of lipids in the bicelle. Thus, the budding approach can be used to determine the preferred curvature of different combinations of lipids and of curvature-inducing proteins.
3.5. Lipid Bilayers with Free Edges in One Direction
The last method, which is included in this section, is a modification of the simple plane membrane. Mahmood et al. investigated the curvature-sensing properties of the F-BAR domain Pacsin1 by generating a bilayer with free edges in one direction, and no pressure coupling in the membrane plane [30]. Thus, the membrane could bend in one direction without having to overcome a restoring force from the periodic boundary condition. A regular grid of Pacsin1 was placed on the membrane and spontaneously induced curvature was monitored. The system was simulated for 2 μs, meaning that the system was surprisingly stable despite having the hydrophobic tails exposed to water in one direction. The same method has been used to investigate the membrane-bending properties of the endosomal sorting complex ESCRT [31].
This entry is adapted from the peer-reviewed paper 10.3390/ijms23158098
References
- Has, C.; Das, S.L. Recent Developments in Membrane Curvature Sensing and Induction by Proteins. Biochim. Biophys. Acta Gen. Subj. 2021, 1865, 129971.
- Warner, H.; Wilson, B.J.; Caswell, P.T. Control of Adhesion and Protrusion in Cell Migration by Rho GTPases. Curr. Opin. Cell Biol. 2019, 56, 64–70.
- Pezeshkian, W.; Marrink, S.J. Simulating Realistic Membrane Shapes. Curr. Opin. Cell Biol. 2021, 71, 103–111.
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingólfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational Modeling of Realistic Cell Membranes. Chem. Rev. 2019, 119, 6184–6226.
- Pezeshkian, W.; König, M.; Wassenaar, T.A.; Marrink, S.J. Backmapping Triangulated Surfaces to Coarse-Grained Membrane Models. Nat. Commun. 2020, 11, 2296.
- Moqadam, M.; Tubiana, T.; Moutoussamy, E.E.; Reuter, N. Membrane Models for Molecular Simulations of Peripheral Membrane Proteins. Adv. Phys. X 2021, 6, 1932589.
- Bar, L.; Perissinotto, F.; Redondo-Morata, L.; Giannotti, M.I.; Goole, J.; Losada-Pérez, P. Interactions of Hydrophilic Quantum Dots with Defect-Free and Defect Containing Supported Lipid Membranes. Colloids Surf. B Biointerfaces 2022, 210, 112239.
- Lee, H. Membrane Penetration and Curvature Induced by Single-Walled Carbon Nanotubes: The Effect of Diameter, Length, and Concentration. Phys. Chem. Chem. Phys. 2013, 15, 16334–16340.
- Duden, R. ER-to-Golgi Transport: COP I and COP II Function. Mol. Membr. Biol. 2003, 20, 197–207.
- Kaksonen, M.; Roux, A. Mechanisms of Clathrin-Mediated Endocytosis. Nat. Rev. Mol. Cell Biol. 2018, 19, 313–326.
- Frost, A.; Unger, V.M.; De Camilli, P. The BAR Domain Superfamily: Membrane-Molding Macromolecules. Cell 2009, 137, 191–196.
- Simunovic, M.; Evergren, E.; Callan-Jones, A.; Bassereau, P. Curving Cells inside and out: Roles of BAR Domain Proteins in Membrane Shaping and Its Cellular Implications. Annu. Rev. Cell Dev. Biol. 2019, 35, 111–129.
- Simunovic, M.; Voth, G.A.; Callan-Jones, A.; Bassereau, P. When Physics Takes Over: BAR Proteins and Membrane Curvature. Trends Cell Biol. 2015, 25, 780–792.
- Jao, C.C.; Hegde, B.G.; Gallop, J.L.; Hegde, P.B.; McMahon, H.T.; Haworth, I.S.; Langen, R. Roles of Amphipathic Helices and the Bin/Amphiphysin/Rvs (BAR) Domain of Endophilin in Membrane Curvature Generation. J. Biol. Chem. 2010, 285, 20164–20170.
- Fjell, C.D.; Hiss, J.A.; Hancock, R.E.W.; Schneider, G. Designing Antimicrobial Peptides: Form Follows Function. Nat. Rev. Drug Discov. 2012, 11, 37–51.
- Kong, R.; Xu, K.; Zhou, T.; Acharya, P.; Lemmin, T.; Liu, K.; Ozorowski, G.; Soto, C.; Taft, J.D.; Bailer, R.T.; et al. Fusion Peptide of HIV-1 as a Site of Vulnerability to Neutralizing Antibody. Nat. Microbiol. 2016, 352, 828–832.
- Hanzal-Bayer, M.F.; Hancock, J.F. Lipid Rafts and Membrane Traffic. FEBS Lett. 2007, 581, 2098–2104.
- Doktorova, M.; Symons, J.L.; Levental, I. Structural and Functional Consequences of Reversible Lipid Asymmetry in Living Membranes. Nat. Chem. Biol. 2020, 16, 1321–1330.
- Cooke, I.R.; Deserno, M. Coupling between Lipid Shape and Membrane Curvature. Biophys. J. 2006, 91, 487–495.
- Yu, H.; Schulten, K. Membrane Sculpting by F-BAR Domains Studied by Molecular Dynamics Simulations. PLoS Comput. Biol. 2013, 9, e1002892.
- Blood, P.D.; Swenson, R.D.; Voth, G.A. Factors Influencing Local Membrane Curvature Induction by N-BAR Domains as Revealed by Molecular Dynamics Simulations. Biophys. J. 2008, 95, 1866–1876.
- Kluge, C.; Pöhnl, M.; Böckmann, R.A. Spontaneous Local Membrane Curvature Induced by Transmembrane Proteins. Biophys. J. 2022, 121, 671–683.
- Lin, M.H.; Hsu, H.J.; Bartenschlager, R.; Fischer, W.B. Membrane Undulation Induced by NS4A of Dengue Virus: A Molecular Dynamics Simulation Study. J. Biomol. Struct. Dyn. 2014, 32, 1552–1562.
- Nawrocki, G.; Im, W.; Sugita, Y.; Feig, M. Clustering and Dynamics of Crowded Proteins near Membranes and Their Influence on Membrane Bending. Proc. Natl. Acad. Sci. USA 2019, 116, 24562–24567.
- Bhaskara, R.M.; Grumati, P.; Garcia-Pardo, J.; Kalayil, S.; Covarrubias-Pinto, A.; Chen, W.; Kudryashev, M.; Dikic, I.; Hummer, G. Curvature Induction and Membrane Remodeling by FAM134B Reticulon Homology Domain Assist Selective ER-Phagy. Nat. Commun. 2019, 10, 2370.
- Siggel, M.; Bhaskara, R.M.; Moesser, M.K.; Dikić, I.; Hummer, G. FAM134B-RHD Protein Clustering Drives Spontaneous Budding of Asymmetric Membranes. J. Phys. Chem. Lett. 2021, 12, 1926–1931.
- Raschle, T.; Hiller, S.; Etzkorn, M.; Wagner, G. Nonmicellar Systems for Solution NMR Spectroscopy of Membrane Proteins. Curr. Opin. Struct. Biol. 2010, 20, 471–479.
- Pannuzzo, M.; Raudino, A.; Böckmann, R.A. Peptide-Induced Membrane Curvature in Edge-Stabilized Open Bilayers: A Theoretical and Molecular Dynamics Study. J. Chem. Phys. 2014, 141, 024901.
- dos Santos Soares, R.D.O.; Bortot, L.O.; Van Der Spoel, D.; Caliri, A. Membrane Vesiculation Induced by Proteins of the Dengue Virus Envelope Studied by Molecular Dynamics Simulations. J. Phys. Condens. Matter 2017, 29, 504002.
- Mahmood, M.I.; Noguchi, H.; Okazaki, K. Curvature Induction and Sensing of the F-BAR Protein Pacsin1 on Lipid Membranes via Molecular Dynamics Simulations. Sci. Rep. 2019, 9, 14557.
- Mandal, T.; Lough, W.; Spagnolie, S.E.; Audhya, A.; Cui, Q. Molecular Simulation of Mechanical Properties and Membrane Activities of the ESCRT-III Complexes. Biophys. J. 2020, 118, 1333–1343.
This entry is offline, you can click here to edit this entry!
