Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Remote Sensing
|
Engineering, Environmental
The creation of an accurate simulation of future urban growth is considered to be one of the most important challenges of the last five decades that involves spatial modeling within a GIS environment. Even though built-up densification processes, or transitions from low to high density, are critical for policymakers concerned with limiting sprawl, the literature on models for urban study reveals that most of them focus solely on the expansion process. Although the majority of these models have similar goals, they differ in terms of implementation and theoretical assumptions. Cellular automata (CA) models have been proven to be successful at simulating urban growth dynamics and projecting future scenarios at multiple scales.
- cellular automata
- urban densification
- urban models
1. Introduction
Urbanization is a multifaceted, worldwide process that reveals itself in rapidly changing human population densities and shifting land-use patterns. In the last 30 years, there has been a rapid growth in urban expansion owing primarily to development policies that prioritized urban growth over agricultural and rural development. Large-scale immigration to cities has resulted in rapid urbanization and land-use change [1]. Accelerating urbanization has put a strain on land resources and resulted in a slew of environmental and social issues [2]. In different countries, the shape or pattern of urban growth varies greatly, but in general, city growth is a twofold process of external expansion and rapid physical growth or internal growth and reorganization [3]. This can be further subdivided into two categories: Urban expansion, which deals with horizontal growth and urban densification; or infill development, which is referred as vertical expansion or in-between development [4].
Globally, many cities and regions have enacted policies aimed at encouraging urban densification through a combination of spatial planning and fiscal or economic measures, as well as encouraging infill development and land recycling [5,6]. Urban densification, through infill development, is frequently addressed in urban planning literature as a possible approach to produce compact communities, curb sprawl, and establish urban sustainability [7,8,9]. For more efficient planning and management, a greater understanding of the process of urban densification and the implications of this growth and land-use change is essential [10]. As a result, several empirical and theoretical modeling tools for the simulation and prediction have recently been developed [11,12].
Urban densification is influenced by various driving factors such as those related to the natural environment, socioeconomics, the built environment, and governance policies, thus making modeling of urban growth complex [13]. Due to their simplicity, versatility, and intuitiveness, CA-based models have been widely used [14]. The application of cellular space models to geographic modeling dates backs to the 1980s [15,16,17]. Building on these ideas and owing to the fact that new generations of hardware and software to simulate CA have been improved upon since the 1900s, a generic modeling framework based on discrete-time, cell-spaced models was proposed for cellular computation [18,19]. Transition rules are used to calculate development probability as a function of neighborhood, a series of geographical parameters, and stochastics disturbance terms which form the base of CA [1,20,21]. Furthermore, CA is highly compatible with the GIS environment. The nature in which CA works has a natural affinity with raster data, as both treat the input as a representation of cells. As a result of this, ref. [22] stated that CA has a high computational and operational efficiency, and that the neighborhood function has an analogous relationship to focal sum or focal mean function, making it suitable for any kind of simulation. These inherent similarities with GIS helped geographers to quickly adopt it as a framework for modeling spatial dynamics [23,24].
Hence, the nature of the CA model to explicitly consider the spatiotemporal dynamics of urban growth makes it more advantageous than other existing models [25]. Recently, there have been many other developments, such as hybrid CA urban models, which incorporate artificial intelligence based on empirical data such as artificial neural networks [26], case-based reasoning (CBR) [27], and colony optimization [28].The increasing uncertainty due to rapid environmental and societal and technological changes makes it crucial to explore multiple urban models, and driving factors have become important. With urban densification being an innovative yet crucial component of global environmental change, this study reviews the CA model in detail, including various integration approaches with other urban models. Moreover, the CA model facilitates movement toward an environment-sensitive modeling [29] which can be used to establish future development pillars and can be utilized to resolve any limitations or shortcomings.
2. Cellular Automata (CA) Model
Cellular automata (CA) are computational methods for simulating the growth of a complex system by describing it with a set of simple rules [30]. It is a system of cells representing a discrete moment and a set of rules, determining the local transfer function based on the current state of an adjacent cell [31]. In the modeling of urban processes, CA models have a number of advantages, including the ability to perform spatial dynamics and time explicitly [32]. Wagner [33] proposed that CA can be considered an analytical engine of GIS after successfully analyzing the similarities and capabilities of CA.
Sgandurra [34] defined a cell as the smallest unit of space made up of only one component. Each cell in the lattice structure known as cellular space is in one of several predetermined states. The law guiding the change between states is known as the local rule. It is particularly important to choose the optimum transition rules for the phenomenon being studied [35]. Since a cell’s finite state machine only accepts input from the neighborhood, it is referred to as “local” in this definition. The term “neighborhood” refers to the cells that are immediately adjacent to a certain cell, and they have the power to affect the subsequent state of that cell. Thus, different states with a CA transition rule will yield different results, but will be similar in statistical form [36].
Understanding the nature of the spatial dynamic requires the use of dynamic models as well as social, economic, and environmental concepts [37]. Over the past few decades, there has been a substantial advancement in various modeling techniques to understand urban expansion [38]. Various simulation and prediction methods have been used in the past to simulate future expansion and a few studies considered densification [39,40,41]. This paper reviews the use of CA models to understand the dynamics of urban densification and various driving factors associated with it.
3. Cellular Automata in Urban Densification
The introduction and implementation of CA models designed to simulate urban land-use change from a bottom-up perspective has radically altered the study of urban systems over the last four decades. While models (in general) are abstractions of reality, few attempts have been made to capture the wider chaotic dynamics of urban densification to date [69]. Due to CA models’ inability to represent entities at the most disaggregated levels, current urban models focus on horizontal urban growth. Recent studies [70,71] have made it more evident that CA-based urban models mainly focus on urban sprawl and expansion.
Traditionally, CA models simulate the spatiotemporal dynamics of land-use structures using grid units that are the same size as a cell lattice, similar to raster pixels or patches [72]. The transition rule is the most significant element in the CA model, and researchers have utilized a variety of methods, such as artificial neural networks [52], genetic algorithms [59], Markov models [73], the Bayesian method [74], kernel functions [28], and support vector machines [75] to produce transition rules.
Vertical urban growth or urban densification is one of the most essential parts of ‘sustainable, low carbon, equitable, resilient development’, as it changes the operation of cities even more [76]. Furthermore, building distribution patterns can have a substantial impact on the nature of the urban heat island effect [77] and can increase pollution levels [78] and road traffic noise levels [79]. Even though CA models for urban densification have recently emerged, there have been studies about 3D CA models [80] which provide an even more realistic representation. As a result, spatial and local variables should be added in order to increase the accuracy of CA simulation [81]. It is significant to understand the various types of drivers and constraints underlying the urban CA models. This would help urban CA modelers to understand the relation between global patterns and local actions, thus acting as a vehicle to construct and validate a new urban model based on “what-if” decision making. CA urban models should also consider qualitative factors such as land ownership and density change by adjusting the models’ parameter settings.
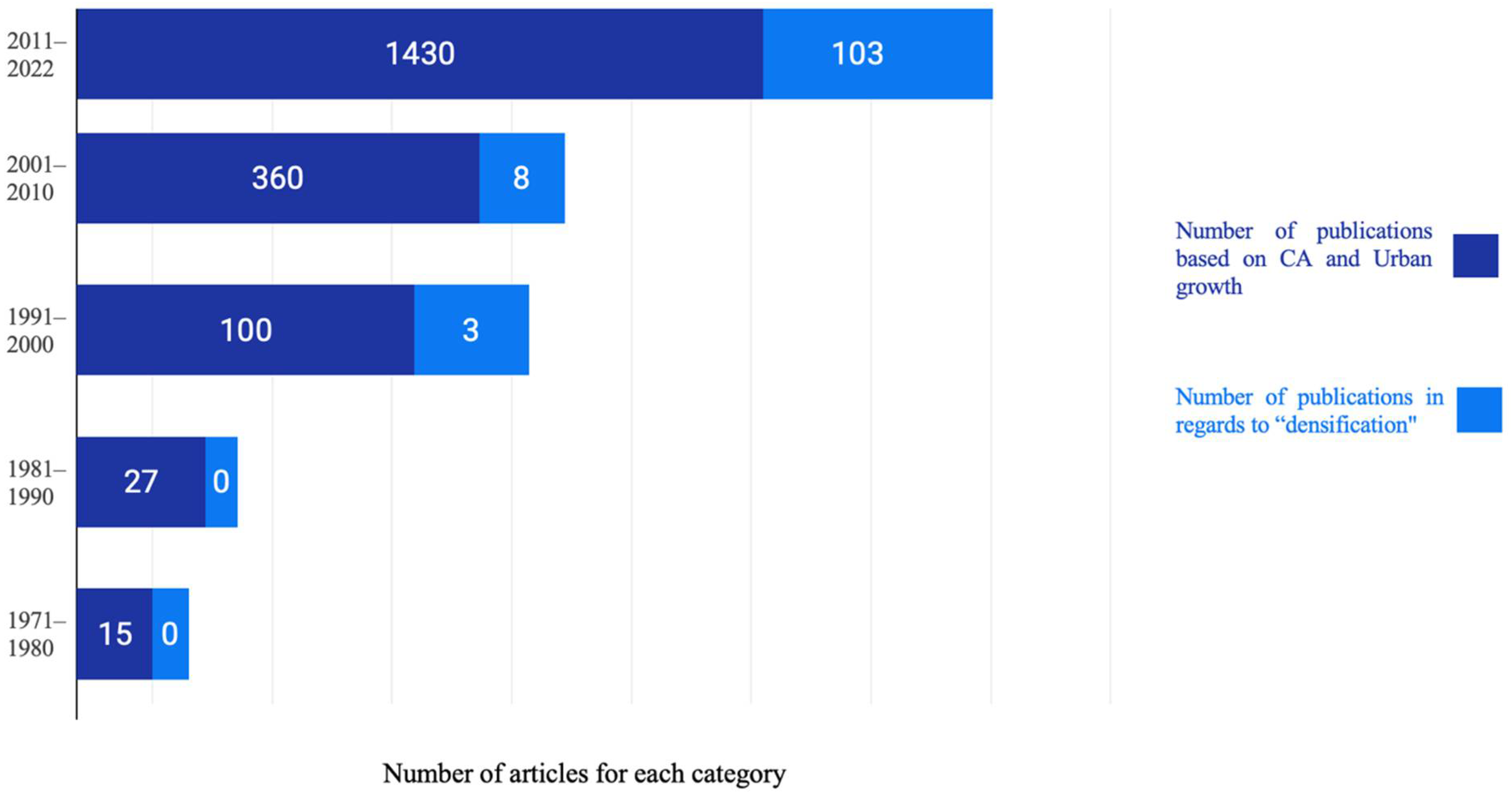
There have been few works carried out with CA and densification in recent years, but the number is insignificant, as seen in the Figure 6. As a result of which, it is crucial to review CA-based urban study scenarios based on the data collected, driving factors, and the undergoing process which produces an accurate model. This can open several possibilities and the necessity to expand the horizon of studying different aspects of urban densification.
Figure 6. Total number of stud
This entry is adapted from the peer-reviewed paper 10.3390/land11071113
This entry is offline, you can click here to edit this entry!
