Seismic Analysis of Slender Monumental Structures: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Maria Giovanna Masciotta
,
Paulo B. Lourenço

The preservation and seismic risk mitigation of built cultural heritage is considered today as a major priority in the international political agenda. Among the great variety of heritage structures spread worldwide, masonry towers belong to one of the most vulnerable categories against earthquake actions due to their morphological and material singularity. The proper understanding of the structural behavior of these artefacts at the micro, meso and macro scales, combined with a thorough knowledge of the best analysis practices deriving from the shared experience of the scientific community working in this field, is a fundamental prerequisite to appropriately address their seismic assessment.

  • historic towers
  • dynamics of slender structures
  • masonry failure mechanisms

1. Introduction

Earthquakes do not kill people, buildings do. Since 1960, 40% of natural disaster deaths occurred due to earthquake events and 60% of these deaths were caused by collapse of masonry buildings [1]. As is widely known, an earthquake is the result of a sudden release of energy in the Earth’s crust that creates seismic waves. These waves result in shaking or rapid movements of the ground, often leading to loss of life and destruction of property. Earthquakes also have the potential to generate a tsunami when the epicenter is located offshore and the seabed abruptly moves, causing displacements of a large amount of water. Past seismic events have clearly shown that structures constructed with strict adherence to seismic safety standards are less likely to be damaged during an earthquake. The Kobe earthquake of 1995, which is counted among the strongest, deadliest, and costliest earthquakes to ever strike Japan and for which the ground shaking in some regions was significantly larger than that considered in the seismic design code of the time, represents an example in this regard. In fact, buildings constructed after the 1981 revision of Japan’s building codes were far less likely to collapse than older buildings during this event; whereas all the reinforced concrete buildings which saw a story collapse were built prior to a 1971 code change regarding beam and column ductility [2]. Although some types of ancient buildings have proved remarkably resistant to earthquake forces for centuries, it must be stressed that their resistance has been achieved only by good conceptual design, with no seismic analysis [3][4]. Besides being conceived in the absence of modern building codes and regulations, more than half of existing heritage buildings are made of unreinforced masonry, thereby featuring a very high seismic vulnerability because of the fragility and inherent complexity of the constituent materials, the frequent use of round unshaped stones, the lack of adequate connections between structural elements or the poor adhesion between units and mortar, to mention a few.
Among the great variety of heritage constructions spread worldwide, slender monumental structures represent a peculiar category still embellishing the skylines and landscapes of many cities. Their main distinguishing feature is the height, which served to guarantee the visibility from the surroundings as a sign of power and to enable the various functions these structures were conceived for, whether as bell or clock towers, watchtowers, chimneys, or minarets. Unlike ordinary masonry buildings, such structures present unique morphological and typological characteristics, which may adversely affect their capability to withstand dynamic actions (e.g., complex geometries, wall thickness, significant dead loads, presence of large openings in elevation, irregularities or contiguity with adjacent buildings) [4][5][6][7][8][9][10][11][12][13][14][15]. Different geometrical and mechanical properties, as well as different boundary conditions, can result in distinct damage patterns under earthquake forces. As far as ancient masonry towers are concerned, the possible collapse mechanisms that can activate with higher probability—based on past earthquake experiences—concern the following [7][8][9][15][16][17][18][19][20]: (1) global overturning of the tower due to the formation of a flexural hinge at the base; (2) vertical splitting of the walls (very frequent in slender towers); (3) diagonal cracking of masonry and overturning of the upper part around the base (Heyman’s rocking mechanisms); (4) combination of diagonal overturing and vertical splitting; (5) failure of the belfry; (6) sliding of the structure along a horizonal crack surface located near the base. When a tower is not extremely slender and depending on the frequency content of the input forces, earthquake-induced flexural damages are commonly associated with significant shear cracks; conversely, in the case of isolated slender towers, a cantilever behavior with flexural failure is mainly expected. The adoption of fairly simple and moderate-cost strengthening measures (e.g., improving the wall integrity and the connection between orthogonal walls) can drastically reduce the high seismic vulnerability exhibited by this type of structures, turning unacceptable failures into acceptable damage scenarios in case of earthquakes.

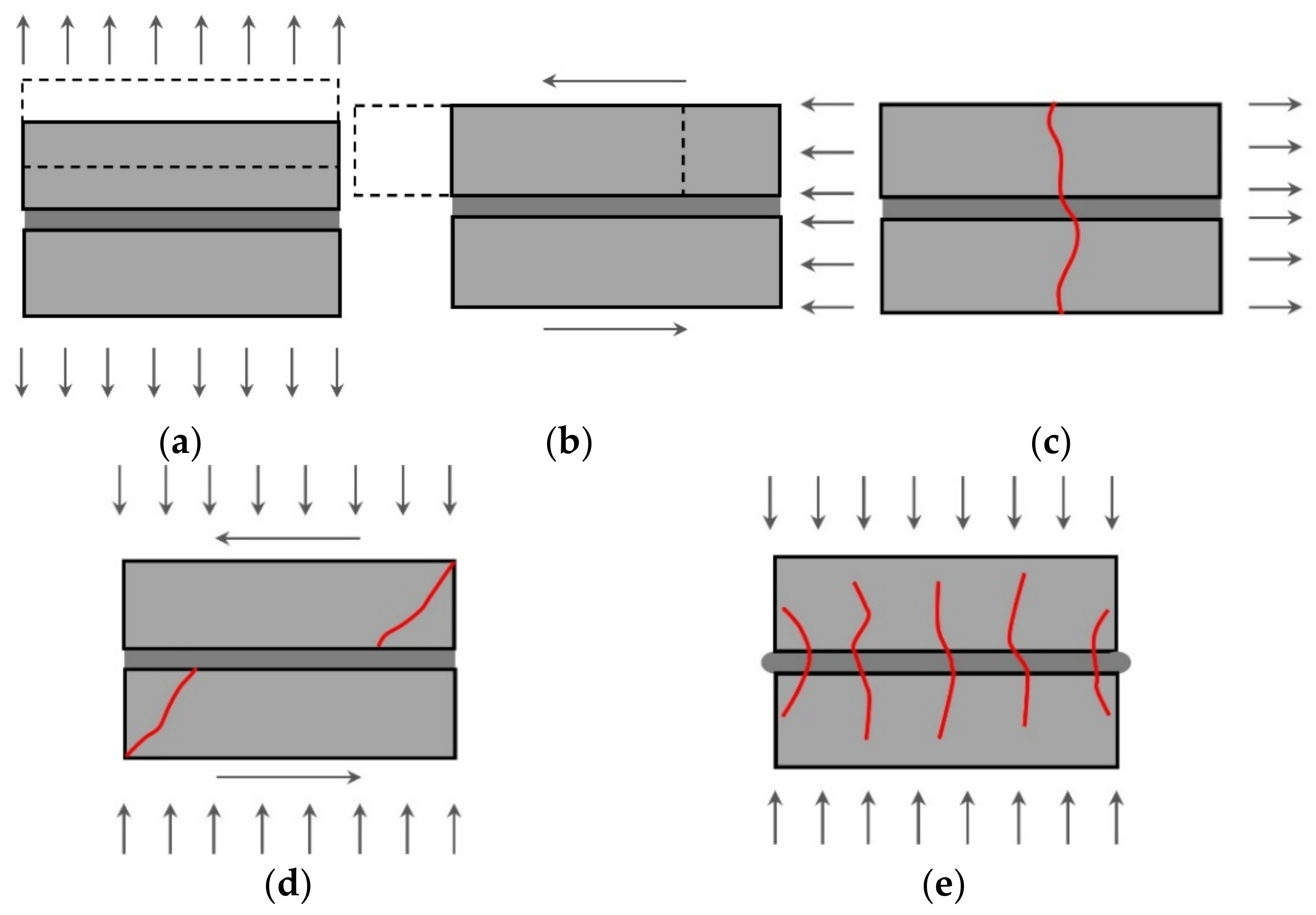
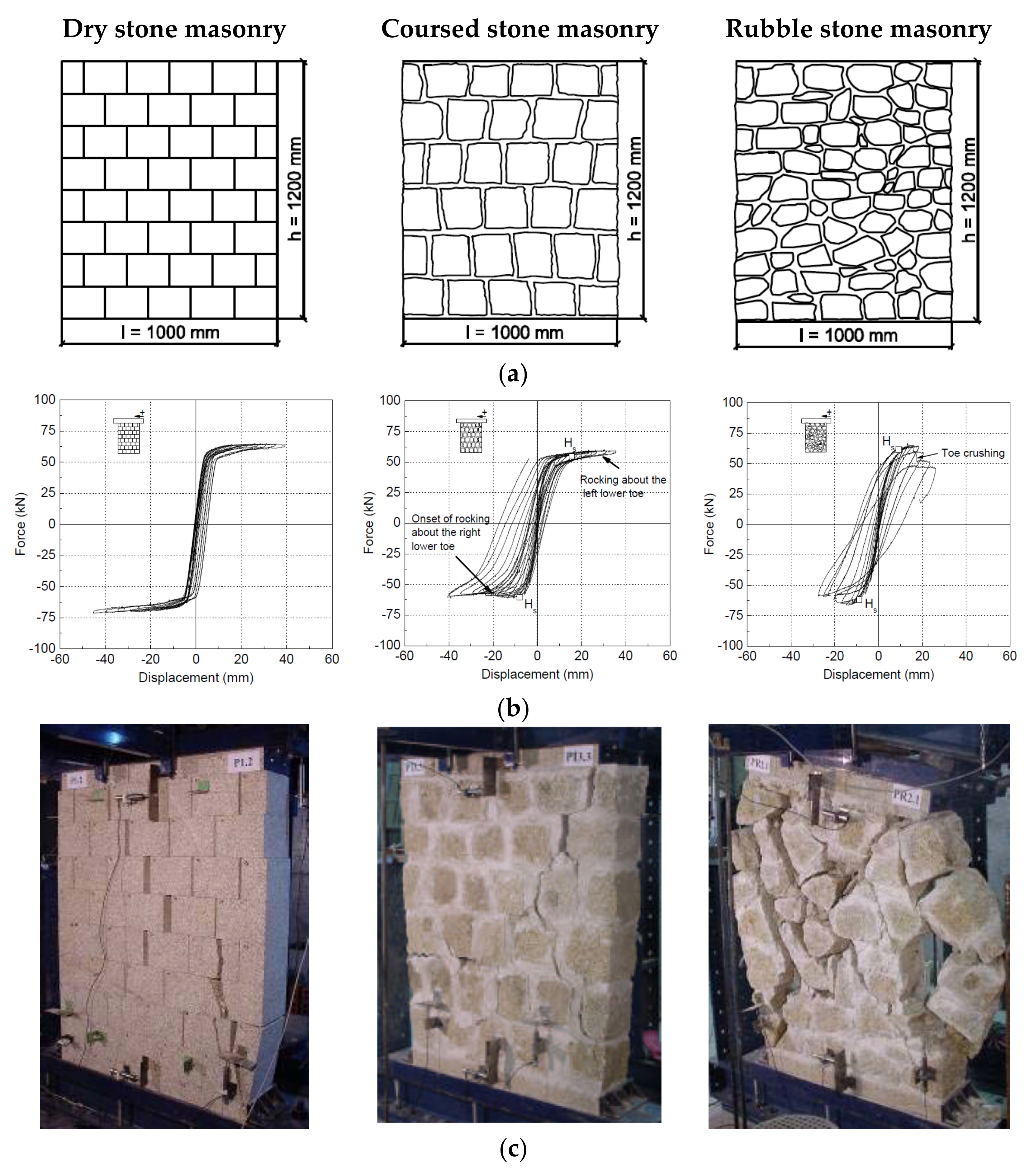
2. Masonry as a Complex Material with Internal Structure

Masonry is a non-homogeneous material formed by units and joints, with or without mortar, and different bond arrangements [21]. Unlike modern masonry, which mainly consists of regularly arranged units, with or without steel reinforcement, ancient masonry is formed by rather complex three-dimensional arrangements of stone or brick units (Figure 1), usually unreinforced. Such a visible internal structure, combined with the variability of materials, unit shape and surface treatments, makes the behavior of historical masonry structures highly indeterminate and difficult to predict and assess with accuracy [22][23][24][25][26].
Applsci 12 07340 g001
Figure 1. Examples of ancient masonry section with complex arrangements of units.
Due to its composite character, masonry mechanics are strongly influenced by the individual properties of its constituents as well as by the bond between them, where the latter is often the weakest link in masonry assemblages. Five basic failure mechanisms can generally occur in masonry [27]: (a) tensile cracking of the joints, (b) shear sliding along the joints, (c) direct tensile cracking of the units, (d) diagonal tensile cracking of the units and (e) compressive crushing (Figure 2). The first two modes are essentially joint mechanisms, where failure occurs at low values of normal stress due to the poor bond strength between joints and units, which is typical for strong unit-weak mortar joint combinations, widely present in ancient stone masonry. The third failure mode is a unit mechanism, which is common in masonry with low-strength units but high-strength mortar, usually with greater tensile bond strength. Instead, the last two failure modes are combined mechanisms involving both units and mortar joints. The preponderance of one failure mode over another or the combination of various failure modes is essentially related to the internal structure of masonry, including the orientation of bed joints with respect to the principal stresses.
Applsci 12 07340 g002
Figure 2. Masonry failure mechanisms (adapted from [27]): (a) joint tensile cracking; (b) joint slipping; (c) unit direct tensile cracking; (d) unit diagonal tensile cracking; (e) masonry crushing.
Figure 3 shows the results obtained from masonry walls with the same geometry but different units shape and arrangement, under combined vertical and cyclic horizontal in-plane loading [21]. Three types of walls are considered, namely dry stone (without mortar), coursed masonry and rubble stone masonry (the last two with the same low-strength mortar). While the in-plane behavior of the dry masonry wall with regular large units is characterized by a rocking response with no strength degradation (no damage in the stones) and remarkable lateral displacement capacity, the response of the coursed masonry wall is predominantly flexural, with a slight strength degradation associated with the progressive spreading of flexural cracks through the joints and a considerable lateral displacement capacity, with rocking mechanisms playing a minor role. By contrast, the response of the rubble masonry wall is essentially controlled by shear, showing a significant strength degradation and a low lateral deformation capability, with consequent brittle failure after the formation of diagonal smeared shear cracks. Despite the geometry and material be the same, distinct failure modes, ultimate lateral strengths and hysteretic behaviors are found for the three walls due to aspects such as roughness of the joints, unit dimensions and interlocking. Randomly assembled masonry typically features very low friction as compared to regularly arranged units with sawn or rough surfaces [28]. The connection between leaves, in case of multi-leaf masonry, also influences the masonry behavior. Past seismic events have shown that the systematic presence of headers between leaves plays a key role in the out-of-plane response of masonry walls; analogously, the presence of proper connection between perpendicular walls or between walls and floors is determinant to ensure a monolithic behavior and prevent out-of-plane failures.
Applsci 12 07340 g003
Figure 3. Experimental results on stone masonry shear walls [21]: (a) specimen geometries; (b) force−displacement diagrams; (c) failure mechanisms.
Despite the existence of common features for masonry, i.e., relatively high resistance in compression, very low tensile strength and anisotropy for different loading directions, the complex mechanical behavior of unreinforced masonry structures cannot be univocally stereotyped since there can be as many different responses as the number of masonry types and specific combinations of geometries and materials.

This entry is adapted from the peer-reviewed paper 10.3390/app12147340

References

  1. Daniell, J.; Wenzel, F.; Schaefer, A. The economic costs of natural disasters globally from 1900–2015. In Natural Disasters Since 1900—Over 8 Million Deaths and 7 Trillion US Dollars Damage, Proceedings of the EGU General Assembly Conference, Vienna, Austria, 17–22 April 2016; EGU General Assembly: Vienna, Austria, 2016; Volume 18, p. 1899. Available online: phys.org (accessed on 20 April 2022).
  2. Ghosh, S. Observations on the performance of structures in the Kobe earthquake of January 17. PCI J. 1995, 40, 14–22.
  3. Fajfar, P. Analysis in seismic provisions for buildings: Past, present and future. In Recent Advances in Earthquake Engineering in Europe; Pitilakis, K., Ed.; Geotechnical, Geological and Earthquake Engineering; Springer: Cham, Switzerland, 2018; Volume 46.
  4. Sarhosis, V.; Milani, G.; Formisano, A.; Fabbrocino, F. Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthq. Eng. 2018, 16, 1511–1545.
  5. Cabboi, A.; Gentile, C.; Saisi, A. From continuous vibration monitoring to FEM-based damage assessment: Application on a stone-masonry tower. Constr. Build. Mater. 2017, 156, 252–265.
  6. Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative seismic vulnerability analysis on ten masonry towers in the coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490.
  7. Valente, M.; Milani, G. Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng. Struct. 2016, 114, 241–270.
  8. Milani, G.; Shehu, R.; Valente, M. A kinematic limit analysis approach for seismic retrofitting of masonry towers through steel tie-rods. Eng. Struct. 2018, 160, 212–228.
  9. Kouris, E.-G.S.; Kouris, L.-A.S.; Konstantinidis, A.A.; Kourkoulis, S.K.; Karayannis, C.G.; Aifantis, E.C. Stochastic Dynamic Analysis of Cultural Heritage Towers up to Collapse. Buildings 2021, 11, 296.
  10. Bartoli, G.; Betti, M.; Biagini, P.; Borghini, A.; Ciavattone, A.; Girardi, M.; Lancioni, G.; Marra, A.M.; Ortolani, B.; Pintucchi, B.; et al. Epistemic Uncertainties in Structural Modeling: A Blind Benchmark for Seismic Assessment of Slender Masonry Towers. J. Perform. Constr. Facil. 2017, 31, 4017067.
  11. Valente, M. Seismic vulnerability assessment and earthquake response of slender historical masonry bell towers in South-East Lombardia. Eng. Fail. Anal. 2021, 129, 105656.
  12. Riva, P.; Perotti, F.; Guidoboni, E.; Boschi, R. Seismic analysis of the Asinelli Tower and earthquakes in Bologna. Soil. Dyn. Earthq. Eng. 1998, 17, 525–550.
  13. Milani, G.; Shehu, R.; Valente, M. Role of inclination in the seismic vulnerability of bell towers: FE models and simplified approaches. Bull. Earthq. Eng. 2017, 15, 1707–1737.
  14. Acito, M.; Bocciarelli, M.; Chesi, C.; Milani, G. Collapse of the clock tower in Finale Emilia after the May 2012 Emilia Romagna earthquake sequence: Numerical insight. Eng. Struct. 2014, 72, 70–91.
  15. Preciado, A.; Santos, J.C.; Silva, C.; Ramírez-Gaytán, A.; Falcon, J.M. Seismic damage and retrofitting identification in unreinforced masonry Churches and bell towers by the september 19, 2017 (Mw = 7.1) Puebla-Morelos earthquake. Eng. Fail. Anal. 2020, 118, 104924.
  16. Ruggieri, S.; Tosto, C.; Rosati, G.; Uva, G.; Ferro, G.A. Seismic Vulnerability Analysis of Masonry Churches in Piemonte after 2003 Valle Scrivia Earthquake: Post-event Screening and Situation 17 Years Later. Int. J. Arch. Herit. 2020, 16, 717–745.
  17. De Matteis, G.; Brando, G.; Corlito, V. Simplified Assessment of the Seismic Vulnerability of Churches after the 2009 L’Aquila Earthquake: An Interdisciplinary Approach; Springer International Publishing: New York, NY, USA, 2019; pp. 1280–1289. ISBN 9783319994406.
  18. Heyman, J. Leaning towers. Meccanica 1992, 27, 153–159.
  19. Valente, M.; Milani, G. Effects of Geometrical Features on the Seismic Response of Historical Masonry Towers. J. Earthq. Eng. 2018, 22, 2–34.
  20. Magrinelli, E.; Acito, M.; Bocciarelli, M. Numerical insight on the interaction effects of a confined masonry tower. Eng. Struct. 2021, 237, 112195.
  21. Vasconcelos, G.; Lourenço, P.B. In-plane experimental behavior of stone masonry walls under cyclic loading. J. Struct. Eng. (ASCE) 2009, 135, 1269–1277.
  22. Milani, G.; Esquivel, Y.W.; Lourenço, P.B.; Riveiro, B.; Oliveira, D.V. Characterization of the response of quasi-periodic masonry: Geometrical investigation, homogenization and application to the Guimarães castle, Portugal. Eng. Struct. 2013, 56, 621–641.
  23. Roca, P.; Cervera, M.; Gariup, G.; Pelà, L. Structural Analysis of Masonry Historical Constructions. Classical and Advanced Approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325.
  24. Sacco, E.; Addessi, D.; Sab, K. New trends in mechanics of masonry. Meccanica 2018, 53, 1565–1569.
  25. D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arc. Computat. Methods Eng. 2020, 27, 1153–1185.
  26. Andreini, M.; De Falco, A.; Giresini, L.; Sassu, M. Mechanical characterization of masonry walls with chaotic texture: Procedures and results of in-situ tests. Int. J. Archit. Herit. 2014, 8, 376–407.
  27. Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1996.
  28. Lourenço, P.B.; Oliveira, D.V.; Milani, G. Computational advances in masonry structures: From mesoscale modeling to engineering application. In Developments and Applications in Computational Structures Technology; Topping, B.H.V., Adam, J.M., Pallarés, F.J., Bru, R., Romero, M.L., Eds.; Saxe-Coburg Publications: Kippen, Scotland, 2016; pp. 1–23.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Feedback