Reconstructing Superquadrics from Intensity and Color Images: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Computer Science, Artificial Intelligence
Contributor:
Darian Tomašević
,
Peter Peer
,
Franc Solina
,
Aleš Jaklič
,
Vitomir Štruc

The task of reconstructing 3D scenes based on visual data represents a longstanding problem in computer vision. Common reconstruction approaches rely on the use of multiple volumetric primitives to describe complex objects. Superquadrics (a class of volumetric primitives) have shown great promise due to their ability to describe various shapes with only a few parameters. Recent research has shown that deep learning methods can be used to accurately reconstruct random superquadrics from both 3D point cloud data and simple depth images. We extend these reconstruction methods to intensity and color images. 

  • superquadrics
  • reconstruction
  • color images
  • deep learning
  • convolutional neural networks

1. Introduction

Scene reconstruction from visual data represents a fundamental field of research in computer vision. Its main goal is to reconstruct an observed environment, as accurately as possible, by describing the various objects in the scene. One of the prevalent reconstruction approaches relies on representing complex scenes via a set of simple geometric shapes, also known as volumetric primitives (the most expressive and versatile of these primitives are currently superquadrics) [1][2]. Since the number of reconstructed primitives can be adjusted, this allows for a rather flexible and detailed solution to the problem. Successfully reconstructed environments can then be used by autonomous agents for various tasks, such as navigating their surroundings [3][4] or grasping objects [5][6], both of which have practical applicability, e.g., in warehousing and manufacturing.
The outlined reconstruction approach, which relies on volumetric primitives, is commonly known as bottom-up reconstruction. It was first introduced to vision systems by Marr [7], whose theoretical vision system utilized various types of depth information to fit appropriate volumetric models in a hierarchical manner. The transition from theoretical systems to practical applications occurred much later and was strongly influenced by the choice of 3D representations. Since detailed representations required a large number of parameters and, thus, more complex models, it was clear that representations with fewer parameters were necessary. Representations, such as shape primitives, would thus allow for less complexity at the expense of reconstruction accuracy, which can often be minimal. Following this train of thought, superquadrics (a class of volumetric primitives) were introduced to computer graphics by Barr [1]. The idea of superquadrics was then carried over to computer vision by Pentland [8]. More formally, superquadrics are 3D models that require only a few shape parameters to form a variety of different shapes, with other parameters describing their size as well as position and rotation in space.
After a long hiatus, the topic of superquadric recovery was revisited, inspired by tremendous advances in deep learning. More recent works relied on the use of convolutional neural networks (CNNs) to recover shape primitives from a scene [9][10][11][12][13][14][15]. These state-of-the-art approaches bypass the computational overhead of early iterative solutions and exhibit considerably higher reconstruction accuracy. They also address reconstruction from different types of data, such as point clouds, depth images, and even a combination of RGB images and mesh data. To achieve successful reconstructions, all approaches adopt learning objectives, which include a certain level of geometric information. Recently, Oblak et al. [13] moved past the constraints of 3D data and showcased that reconstruction of superquadrics from a single depth image is possible with the use of deep learning. The authors relied on a CNN predictor, trained with a custom geometry-based loss, to estimate the size, shape, position, and rotation of a depicted superquadric.
While modern superquadric recovery approaches do achieve incredible reconstruction accuracy, they remain limited in terms of input data (to point cloud data or depth images). Unfortunately, despite advancements in sensor technologies, such types of data remain quite difficult to obtain, especially for arbitrary tasks or situations. This, in turn, significantly limits the applicability of these reconstruction methods. Meanwhile, mechanisms for gathering RGB images are already prevalent and could be easily exploited given a suitable reconstruction approach.
In this study, we address the need for an RGB-based superquadric recovery solution, which is capable of reconstructing unknown objects in an uncontrolled environment. To achieve this, we followed the general idea of recent methods [12][13] based on depth images but took a step further and explored the usage of deep learning models for reconstruction of superquadrics from a single RGB image. The main challenge we faced: RGB images lack the invaluable spatial information provided by depth images, which is extremely important for correctly predicting the position of superquadrics in space. We took a gradual approach to solve the reconstruction task, by training and evaluating the predictor on increasingly complex images. We propose two methods for dealing with the lack of spatial information in RGB images. The first method is based on fixing the z position parameter of the superquadrics, which in turn removes the ambiguity in (superquadric) position and size. The second method relies on the addition of shadow-based cues to superquadric images to obtain the required spatial information. For this approach, we drew inspiration from similar works that leveraged shadow-based cues to recover the shapes or sizes of objects [16][17].
To facilitate this study, we experimented with fixed-sized images (i.e., 256×256 pixels), which included only one superquadric, allowing us to focus only on the reconstruction task. We first limited ourselves to simple intensity images with gray superquadrics on a black background and then moved to RGB images with randomly colored or textured superquadrics and backgrounds. To evaluate our results, we used both qualitative and quantitative techniques in the form of visualized reconstructions of superquadrics as well as error distributions of superquadric parameters and accuracy distributions of the predictions. We also compared our results with results based on Oblak et al. [13] and reflected on the differences between the analyzed problems. In addition, we compared our method to the state-of-the-art solution for a similar task, proposed by Paschalidou et al. [10].
Previous superquadric recovery approaches have already shown promising results in practical applications, most notably in robot grasping tasks [18][19][20][21]. Other interesting applications include handling of mail pieces [22], documentation of artifacts [23][24], and recently, the representation of the human body [25]. However, these practical applications are again based on point cloud data or depth images. By successfully recovering superquadrics from a single RGB image, we aim to widen the use and applicability of superquadric reconstruction approaches, due to the mass availability of such data. In our work, we also avoid the need for manually labeled real-world data, which is difficult to obtain, by training and testing the CNN predictor on synthetic images and later observing how well the model generalizes to real images. 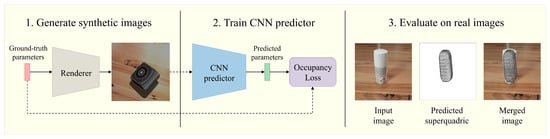An overview of our method and the discussed phases are present in Figure 1. As we show, we are able to approximate various simple real-world objects with superquadrics, from just a single real-world RGB image, without any camera calibration. We believe that this approach could be tremendously useful for future robot-grasping approaches, especially when the object shapes are not known in advance, since it requires minimal human interaction.
Sensors 22 05332 g001 550
Figure 1. Visualized overview of our reconstruction method. (1) Generate a large dataset of synthetic images that mimic the real environment. Each image contains a randomly positioned superquadric of a random shape. (2) Train the CNN predictor on the synthetic dataset to predict superquadric parameters. (3) Use the final CNN predictor (Textured on Wood (Fixed z) with Sh. & S.L.) on real images to reconstruct simple objects as superquadrics.

2. Superquadric Recovery

The process of superquadric recovery entails estimating superquadric parameters (size, shape, position, and rotation) from the given input data so that the reconstructed superquadric fits the data as closely as possible.
Recently, the topic of superquadric recovery experienced a resurgence of interest, driven mostly by advancements in deep learning and convolutional neural networks (CNNs). Tulsiani et al. [9] presented a method for reconstructing 3D objects with the use of cuboids as the primitive representations but noted the limits of this representation. Continuing this line of thought, Paschalidou et al. [10] modified the approach to use superquadrics and in turn, achieved substantially better reconstruction results, due to the tremendous range of shapes that superquadrics can represent. However, to train the CNN predictor, this work relied on labeled 3D data, including models of various object categories, such as human bodies or vehicles. This approach was later adapted [11] to recover superquadrics, in a hierarchical and unsupervised manner, given a single RGB image of a 3D model from the predefined categories. Another reconstruction approach was also proposed by Li et al. [15], which achieved segmentation of point cloud data into parts in an unsupervised manner. Despite tremendous advancements, reliance on labeled 3D data limits the applicability of these approaches to arbitrary data.
To address the need for a more generalized solution, Oblak et al. [12] introduced a supervised deep learning approach, inspired by previous work [2], for estimating the superquadric parameters from a single depth image under the constraint that the orientation of the superquadric was fixed. Šircelj et al. [14] built upon this method and achieved segmentation and recovery of multiple superquadrics. A different avenue was taken by Slabanja et al. [26], who focused on reconstruction from point cloud data. Most recently, Oblak et al. [13] extended their previous work by introducing a novel geometry-aware learning objective, which allows the model to also predict parameters of rotated superquadrics. They also proposed two learning strategies, an explicit and an implicit variant. Despite their success, these approaches are limited to either 3D data or depth images. Unfortunately, for arbitrary tasks, both types of data remain rather difficult to obtain, at least when compared to RGB images. To address this gap, we present a solution that is able to recover high-quality superquadric models from only a single RGB image.

3. Deep Learning and 3D data

Although this work focuses on superquadric recovery from 2D data, some relevant concepts are closely related to recent deep learning techniques designed for 3D data. Below, we discuss the main overlapping topics between the two problem domains, i.e., the choice of data representation and issues related to pose estimation.
Choice of Data Representation. To tackle the task at hand, we must first decide how the input data will be represented. In recent work, Wu et al. [27] proposed representing 3D shapes with 3D discretized volumetric grids and presented a deep 3D encoder model, 3D ShapeNet, capable of reconstructing complete 3D shapes given the grid input. In their approach, they also utilized an additional deep model, with which they transformed the initial depth images into 3D volumetric representation. With MarrNet, Wu et al. [28] extended their approach to 2D RGB input images, in which they performed 2.5D sketch estimation, with the use of an encoder–decoder architecture. From the 2.5D data, they then estimated the volumetric grid and the 3D shape of the object with a 3D decoder. While volumetric grids allow for the representation of true 3D data, one of the main shortcomings of such approaches are the 3D encoders, which have a significant impact on system performance and memory consumption.
In comparison, working only with 2D data and 2D encoders drastically reduces system requirements. However, normal 2D images only offer a single perspective of the scene and are thus prone to object self-occlusion and, in turn, loss of information. Recently, Oblak et al. [12][13] proposed reconstructing 3D objects directly from depth images (2.5D data), which encode invaluable 3D information in a 2D structure. Their approach exploits this intrinsic encoding property and only requires 2D encoders to function. To allow for the reconstruction from simple 2D RGB images, we must conquer the challenges presented by the lack of spatial information, such as determining the positions of objects in space.
Pose Estimation Issues. The most recent approaches for estimating the position of an object in space use CNN-based models to estimate the pose parameters from a given continuous range of values. For example, Miao et al. [29] estimated all pose-related parameters (position and rotation) with six separate regressors and a mean squared error (MSE) loss. Another example is the work by Zhu et al. [30], who trained their pose regressor alongside a standard volumetric reconstruction encoder–decoder model. Despite the success of these methods, other approaches based on geometry-aware loss functions have been shown to perform better than regular MSE loss-based approaches. A recent approach by Xiang et al. [31], for example, showcased the strength of such approaches, by minimizing the distance between surface points of rotated objects.
To achieve successful pose estimation, it is also important to consider how the rotation of objects is described. While we often associate Euler angles with rotation, they can be rather problematic since they suffer from gimbal lock. In comparison, using quaternions to represent rotation, solves this issue. On the other hand, relying on quaternions typically involves using the unit norm constraint, which slightly complicates the regression task [30]. Oblak et al. [12][13] combined the above-mentioned methods to estimate the size, shape, position, and rotation of superquadrics. Their results showcase the importance of using a geometry-based loss function for training, as well as quaternions over Euler angles for representing the rotation of superquadrics. In our work, we also rely on the combined approach to estimate superquadrics from intensity and color images. 

4. Conclusions

In our work, we addressed the problem of recovering superquadrics from intensity and color images of varying complexities. Our proposed method extends the method presented in previous research on superquadric recovery from depth images [13]. We showcase that recovery of superquadrics is also possible from 2D images and that it can be just as accurate as recovery from depth or 2.5D images, despite the lack of spatial information. To achieve this, we propose modifying the training images and ground truth parameters in one of two ways, either by fixing one of the position parameters or by introducing shadows into the scenes. With both approaches, our method achieves considerably better reconstruction results on synthetic images than the current state-of-the-art methods [10]. Additionally, we show that our model can generalize well from synthetic data to real-world images and is able to reconstruct simple unknown objects with a single superquadric. However, performances on real images can be rather unpredictable and require custom synthetic datasets that mimic the given environment.
Our findings showcase the potential of using a deep learning approach based on superquadrics for the 3D reconstruction of unknown objects from a single 2D image, without the need for camera calibration. There exist a myriad of possible future directions. As a next step, we test our approach on real-world tasks, such as a robot grasping random objects, where the Fixed z position assumption might be a good approximation of real-world conditions. We believe it would be possible to obtain successful reconstructions even in new environments with minimal human interactions, by simply fine-tuning the model on newly generated synthetic images, whose background matches the new environment. Another avenue of future research includes superquadric recovery from more than one image, for example, from a multi-view camera setup, which could provide necessary spatial information to improve the overall accuracy of our method. Performances on real data could also be improved by texturing synthetic superquadrics more realistically. This work could also be expanded to support the recovery and segmentation of multiple superquadrics to describe more complex objects.

This entry is adapted from the peer-reviewed paper 10.3390/s22145332

References

  1. Barr, A.H. Superquadrics and angle-preserving transformations. IEEE Comput. Graph. Appl. 1981, 1, 11–23.
  2. Solina, F.; Bajcsy, R. Recovery of parametric models from range images: The case for superquadrics with global deformations. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 131–147.
  3. Khosla, P.; Volpe, R. Superquadric artificial potentials for obstacle avoidance and approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 1778–1784.
  4. Smith, N.E.; Cobb, R.G.; Baker, W.P. Incorporating stochastics into optimal collision avoidance problems using superquadrics. J. Air Transp. 2020, 28, 65–69.
  5. Mahler, J.; Matl, M.; Satish, V.; Danielczuk, M.; DeRose, B.; McKinley, S.; Goldberg, K. Learning ambidextrous robot grasping policies. Sci. Robot. 2019, 4, eaau4984.
  6. Morrison, D.; Corke, P.; Leitner, J. Learning robust, real-time, reactive robotic grasping. Int. J. Robot. Res. 2020, 39, 183–201.
  7. Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 1982.
  8. Pentland, A.P. Perceptual organization and the representation of natural form. Artif. Intell. 1986, 28, 293–331.
  9. Tulsiani, S.; Su, H.; Guibas, L.J.; Efros, A.A.; Malik, J. Learning shape abstractions by assembling volumetric primitives. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2635–2643.
  10. Paschalidou, D.; Ulusoy, A.O.; Geiger, A. Superquadrics revisited: Learning 3D shape parsing beyond cuboids. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10344–10353.
  11. Paschalidou, D.; Gool, L.V.; Geiger, A. Learning unsupervised hierarchical part decomposition of 3D objects from a single RGB image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1060–1070.
  12. Oblak, T.; Grm, K.; Jaklič, A.; Peer, P.; Štruc, V.; Solina, F. Recovery of superquadrics from range images using deep learning: A preliminary study. In Proceedings of the IEEE International Work Conference on Bioinspired Intelligence (IWOBI), Budapest, Hungary, 3–5 July 2019; pp. 45–52.
  13. Oblak, T.; Šircelj, J.; Štruc, V.; Peer, P.; Solina, F.; Jaklič, A. Learning to Predict Superquadric Parameters From Depth Images With Explicit and Implicit Supervision. IEEE Access 2020, 9, 1087–1102.
  14. Šircelj, J.; Oblak, T.; Grm, K.; Petković, U.; Jaklič, A.; Peer, P.; Štruc, V.; Solina, F. Segmentation and recovery of superquadric models using convolutional neural networks. In Proceedings of the 25th Computer Vision Winter Workshop, Rogaška Slatina, Slovenia, 3–5 February 2020; pp. 1–5.
  15. Li, S.; Liu, M.; Walder, C. EditVAE: Unsupervised Part-Aware Controllable 3D Point Cloud Shape Generation. arXiv 2021, arXiv:2110.06679.
  16. Abrams, A.; Miskell, K.; Pless, R. The episolar constraint: Monocular shape from shadow correspondence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1407–1414.
  17. Xie, Y.; Feng, D.; Xiong, S.; Zhu, J.; Liu, Y. Multi-Scene Building Height Estimation Method Based on Shadow in High Resolution Imagery. Remote Sens. 2021, 13, 2862.
  18. Vezzani, G.; Pattacini, U.; Natale, L. A grasping approach based on superquadric models. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1579–1586.
  19. Makhal, A.; Thomas, F.; Gracia, A.P. Grasping unknown objects in clutter by superquadric representation. In Proceedings of the 2nd IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 31 January–2 February 2018; pp. 292–299.
  20. Vezzani, G.; Pattacini, U.; Pasquale, G.; Natale, L. Improving Superquadric Modeling and Grasping with Prior on Object Shapes. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6875–6882.
  21. Haschke, R.; Walck, G.; Ritter, H. Geometry-Based Grasping Pipeline for Bi-Modal Pick and Place. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 4002–4008.
  22. Solina, F.; Bajcsy, R. Range image interpretation of mail pieces with superquadrics. In Proceedings of the National Conference on Artificial Intelligence, Seattle, WA, USA, 13–17 July 1987; Volume 2, pp. 733–737.
  23. Jaklič, A.; Erič, M.; Mihajlović, I.; Stopinšek, Ž.; Solina, F. Volumetric models from 3D point clouds: The case study of sarcophagi cargo from a 2nd/3rd century AD Roman shipwreck near Sutivan on island Brač, Croatia. J. Archaeol. Sci. 2015, 62, 143–152.
  24. Stopinšek, Ž.; Solina, F. 3D modeliranje podvodnih posnetkov. In SI Robotika; Munih, M., Ed.; Slovenska Matica: Ljubljana, Slovenia, 2017; pp. 103–114.
  25. Hachiuma, R.; Saito, H. Volumetric Representation of Semantically Segmented Human Body Parts Using Superquadrics. In Proceedings of the International Conference on Virtual Reality and Augmented Reality, Tallinn, Estonia, 23–25 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 52–61.
  26. Slabanja, J.; Meden, B.; Peer, P.; Jaklič, A.; Solina, F. Segmentation and reconstruction of 3D models from a point cloud with deep neural networks. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 17–19 October 2018; pp. 118–123.
  27. Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920.
  28. Wu, J.; Wang, Y.; Xue, T.; Sun, X.; Freeman, B.; Tenenbaum, J. MarrNet: 3D Shape Reconstruction via 2.5D Sketches. Adv. Neural Inf. Process. Syst. 2017, 30, 540–550.
  29. Miao, S.; Wang, Z.J.; Liao, R. A CNN regression approach for real-time 2D/3D registration. IEEE Trans. Med. Imaging 2016, 35, 1352–1363.
  30. Zhu, R.; Kiani Galoogahi, H.; Wang, C.; Lucey, S. Rethinking reprojection: Closing the loop for pose-aware shape reconstruction from a single image. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 57–65.
  31. Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. PoseCNN: A Convolutional Neural Network for 6D Object Pose Estimation in Cluttered Scenes. In Proceedings of the 14th Robotics: Science and Systems (RSS), Pittsburgh, PA, USA, 26–30 June 2018; pp. 1–10.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback