The evaluation of rural spatial sustainability refers to the classification of research problems. That is, with the goal of sustainable development and the spatial resources of rural areas as the evaluation object, it aims to improve one or more aspects of rural sustainability by identifying and even improving the spatial layout. Generally, existing rural spatial evaluations are closely related to the term “spatial decision-making”, which in turn guides the selection of subsequent programs or strategies^{[ 1 ]}. The existing evaluation of rural space, aiming at sustainability, involves many aspects, such as natural resources, public facilities, energy services, and planning and design. Previous studies have demonstrated that rural-related spatial evaluation or decision making is a complex task ^{[ 2 ]}. Therefore, achieving sustainability goals also requires new approaches to decision making based on knowledge production^{[ 3 ]}. Over the past two decades, multi-criteria decision-making analysis methods have been applied in related fields to assist decision makers. Multi-criteria decision-making analysis may be an effective and efficient option for solving such problems.

Multi-criteria decision making (or multi-criteria decision-making analysis, hereafter referred to as MCDA) is a basic scientific method used to select the best alternative, classify alternatives, or rank alternatives in order of preference ^{[ 4 ]}. The term MCDM is used for all methods and techniques that involve multiple conflicting criteria used by decision makers to derive preferences ^{[ 6 ]}. MCDA originated in the field of operations research^[7]. After evolution and development, MCDA has been widely used in management science, environmental science, geography, material science, energy, mathematics, information and computer science, etc. In recent years, MCDA methods have been used to assist decision making related to sustainability. To date, more than 100 MCDA methods have been used in practice, including original methods, derived methods, and combined methods, but only a few MCDA methods have been applied to solving rural spatial evaluation problems.

As a comprehensive evaluation method, MCDA is suitable for solving complex problems characterized by uncertainty, conflicting goals, information heterogeneity, and diversity of interests or viewpoints, in addition to explaining dynamic development systems under the influence of multiple factors . In contrast to the traditional single-criteria analysis method, the MCDA method has advantages because it can obtain the comprehensive score or the ranking of the objects under the influence of multiple criteria ^[8]. From the perspective of the attribute of the judgment subject, MCDA methods can be divided into three categories: multi-objective decision-making analysis (MODA), multi-attribute decision-making analysis (MADA), and comprehensive MCDA ^[9]. From the perspective of the operation process and system composition, Figure 1 clearly shows the six operational steps and the three sub-systems of the MCDA method.

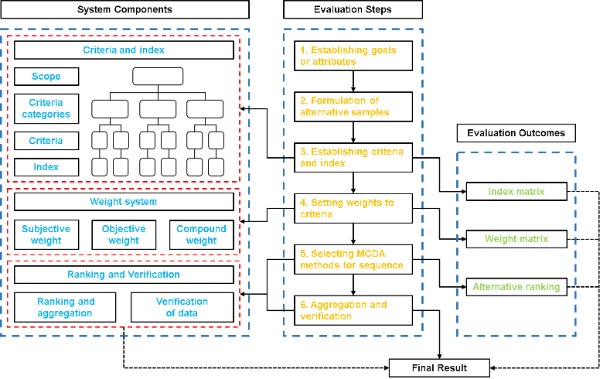Figure 1. Operation process and system composition of MCDA.

At present, there is no unified classification standard for the criteria, but evaluation research aiming at sustainability usually divides the criteria into three categories: society, the economy, and the environment ^[10]. The index is used as a quantitative basis for measuring the quality of the criteria. From the perspective of using functions, Table 2 divides the MCDA methods commonly used in sustainability evaluation into weighting methods and ranking methods, and some methods have both functions . The weighting methods can be divided into the subjective weighting method and objective weighting method. The subjective weighting method depends only on the preference of the decision maker, and not on the quantitative measured data of the evaluation target. In contrast, the objective weighting method is obtained mathematically through the analysis of the initial data ^[11]. Both methods have their advantages and disadvantages. Subjective weighting is more explanatory and misleading, and objective weighting is resistant to interference, but sometimes exceeds the limits of research assumptions. Usually, in a complete multi-criteria decision-making process, at least one weighting method and ranking method are required.

Table 2. Classification of MCDA methods based on functional perspective.

Method	Function	Introduction
AHP	Subjective weight ranking	AHP was first developed by Saaty (1980). It consists of a pairwise comparison, using relative values of criteria (weights) and a score scale on alternatives against criteria. Typically, eigenvalue techniques or regression analysis are used to determine the ordering. AHP is one of the most common MCDA methods.
ANP	Subjective weight ranking	The analysis process of ANP and AHP is roughly the same, but in contrast to the one-way process of AHP, ANP has a feedback mechanism.
BP network	Objective weight ranking	BP network is a type of supervised network based on error back-propagation. Through the calculation and feedback of input information, output information, and the error, the weights of neurons in each layer of the BP network can be modified to obtain the minimum error signal and form the final network model. The learning process of the neural network is mainly the updating process of weights.
BWM	Subjective weight ranking	BWM can obtain weights for different criteria based on pairwise comparisons, requiring less comparison data. Quite differently from AHP, BWM only performs reference comparisons, which means it only needs to use numbers between 1 and 9 to determine the preference of the best criterion over all other criteria and the preference of all criteria over the worst criterion. This process is easier, more accurate, and less redundant because it does not perform quadratic comparisons.
DEA	Objective weight ranking	DEA is a nonparametric productivity measure for multiple-input and multiple-output operations. The method combines and converts multiple inputs and outputs into a single efficiency metric. This approach first establishes an “efficient frontier” formed by a set of decision-making units (DMUs) exhibiting best practices, and then assigns efficiency levels to other non-boundary units based on their distances to the efficient frontier. Finally, the efficiency level of each object is obtained.
Delphi	Objective weight	The Delphi method is a systematic, interactive method that relies on a group of independent experts. Based on this principle, Delphi uses carefully selected experts to answer questionnaires to determine weights. After each round, the summary of the previous round of expert selection and the reasons for their judgment will be fed back to the experts. During this process, the floating range of the weights will shrink and gradually converge towards the “correct” weights. Finally, the process is stopped according to predefined rules.
DEMATEL	Ranking	DEMATEL is considered for an effective method for identifying the components of the causal chain of complex systems. It handles the interdependencies among the evaluation factors and finds the key factors through a visual structural model. The DEMATEL technique can convert the interrelationships between factors into an understandable structural model of the system and divide it into cause and effect groups. Its operation consists of four steps: 1. establish an influence matrix; 2. create a normalized matrix; 3. build a total influence matrix; 4. generate an influence graph.
ELECTRE	Ranking	ELECTRE is a technique for selecting the best alternative from a given set of alternatives. It uses pairwise comparisons of alternatives and sets ranking relationships on them. For example, if a is at least as good as b for criterion i, then alternative a is ranked higher than the alternative b. The ELECTRE tool has evolved over time into different sequential versions, such as ELECTRE I, II, III, IV, and ELECTRE TRI.
Entropy	Objective weight	Information entropy is a measure of the degree of disorder in a system. It can measure the amount of useful information with the data provided. When the value difference between the evaluation objects of the same indicator is large, but the entropy is small, it means that the indicator provides more useful information, and the weight of the indicator should be set correspondingly high.
Fuzzy	Subjective weight Ranking	Due to the availability and uncertainty of information, as well as the ambiguity of human perception and cognition, most selection parameters cannot be given accurately. The fuzzy set provides a mathematical model to determine the membership degree of each element to the set, so that the applicability evaluation data of various subjective standards and the weight of the standard are converted into numerical values by the language of the decision maker.
Grey relation	Ranking	The grey relational method is a branch of grey system theory developed in 1980. The method is similar to TOPSIS, which defines the grey relational degree to represent the closeness between the alternatives. Typically, ideal scenarios are defined and the degree of relevance of alternatives to them is calculated. The most relevant alternative has the shortest distance from the ideal solution and the longest distance from the worst solution.
MAVT (MAUT)	Ranking	MAUT is a systematic approach that takes into account decision makers’ preferences in the form of a utility function defined over a set of attributes. Its functional form is determined by applying preference validation and setting certain utility-independent conditions. The formula is extended to derive a multi-attribute utility function. In the case of MAVT, the difference between utility and value is that the function uses attribute values instead of quantitative attribute measures in a cardinal scale.
OWA	Ranking	The OWA method is similar to WLC, but considers two sets of weights. The first set of weights controls the relative contributions of specific criteria, and the second set of weights controls the order in which the weighted criteria are aggregated. The advantage of OWA is that a variety of different solutions and forecast scenarios can be generated by reordering and changing standard parameters.
PCA	Objective weight	The modeling properties of PCA are largely rooted in regression thinking: variation explained by principal components. After introducing the idea of linear combination of variables, the change in principal components is emphasized. When there is a certain correlation between the two variables, it can be explained that the information of the two variables reflecting the subject overlaps to a certain extent. Principal component analysis is to delete duplicate or irrelevant variables for all the variables originally proposed, and establish as few new variables as possible, so that these new variables are unrelated to each other. Finally, the importance of the variable is obtained.
PCM	Subjective weight	In the pairwise comparison method, participants are presented with a worksheet and asked to compare the importance of two criteria at a time. The scoring scale can be varied, for example, an odd scale of 1 to 9 is often used. Results are combined by adding the scores obtained for each criterion, when the preferred criterion is compared with the criterion to which it is compared. The results are then normalized to a total of 1.0. This weighting method provides a framework for comparing each criterion to all others and helps to show differences in importance between criteria.
Regime	Ranking	The regime method is a discrete multiple evaluation method suitable for evaluating projects and policies by processing qualitative and quantitative information. It uses pairwise comparisons to evaluate the performance of alternatives and establishes ranking relationships among alternatives. The framework of the method is based on two kinds of input data: an influence matrix and a set of weights.
SAW	Ranking	The SAW method, originally applied by Charles (1954), is one of the most commonly used MCDM techniques. The method performs a simple multi-product summation of each criterion score through the corresponding attribute weights to find an overall performance measure for each alternative.
SWOT	Ranking	SWOT analysis is a common tool for strategic planning and a form of brainstorming. It helps organizations better understand their internal and external business environment when making strategic plans and decisions by analyzing and locating their resources and environments in terms of four areas: strengths, weaknesses, opportunities, and threats.
TOPSIS	Ranking	TOPSIS means that the optimal selection scheme has the shortest Euclidean distance from the ideal solution and the largest distance from the negative ideal solution. Intuitively, based on the distance from the ideal solution, the method can take any number of attributes as input. However, TOPSIS can produce unreliable results, and it also does not account for the uncertainty of the weights.
TOWS	Ranking	TOWS matrix is a derivative type of SWOT. In contrast to the SWOT method, TOWS focuses more on the solution strategy obtained through the situation analysis. The matrix includes four strategies: WT, WO, ST, and SO.
VIKOR	Ranking	The VIKOR method is similar to the TOPSIS method in that both are based on distance measurements. In contrast to the strict sorting of TOPSIS, VIKOR seeks a compromise solution. The VIKOR method can also provide clustering capabilities when faced with alternatives.
WASPAS	Ranking	The WASPAS method combines the historical data and current data, and adds the weighted sum model (WSM) and the weighted product model (WPM) to determine the decision target under the corresponding decision criterion.
WLC	Ranking	WLC is an evaluation function method, and is a method of solving multi-objective/attribute programming problems by assigning corresponding weight coefficients to each objective according to its importance, and then optimizing its linear combination.

This entry is adapted from the peer-reviewed paper 10.3390/ijerph19116572