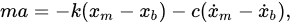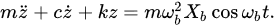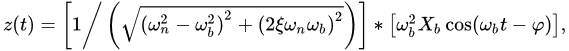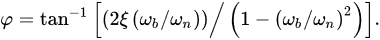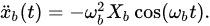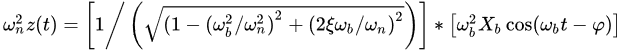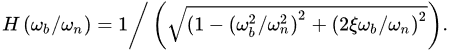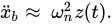Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Optical accelerometers are high-precision inertial sensors that use optical measurement technology to achieve high-precision and electromagnetic interference-resistant acceleration measurements. With the intensive research and development of optical accelerometers in recent years, their applications in inertial navigation, structural health monitoring, precision vibration isolation systems, wind turbine fault monitoring, earthquake monitoring, and other low-frequency vibration detection have flourished. Optical accelerometers have various schemes; however, their characteristics vary considerably due to different optical modulation schemes. This study aims to address the lack of systematic evaluation of currently available low-frequency optical accelerometers. Optical accelerometers can be classified into four categories in accordance with their optical modulation schemes: optical path-, optical intensity-, optical phase-, and optical wave-length-modulated accelerometers.
- accelerometer
- optical sensing systems
1. Principle of Accelerometer
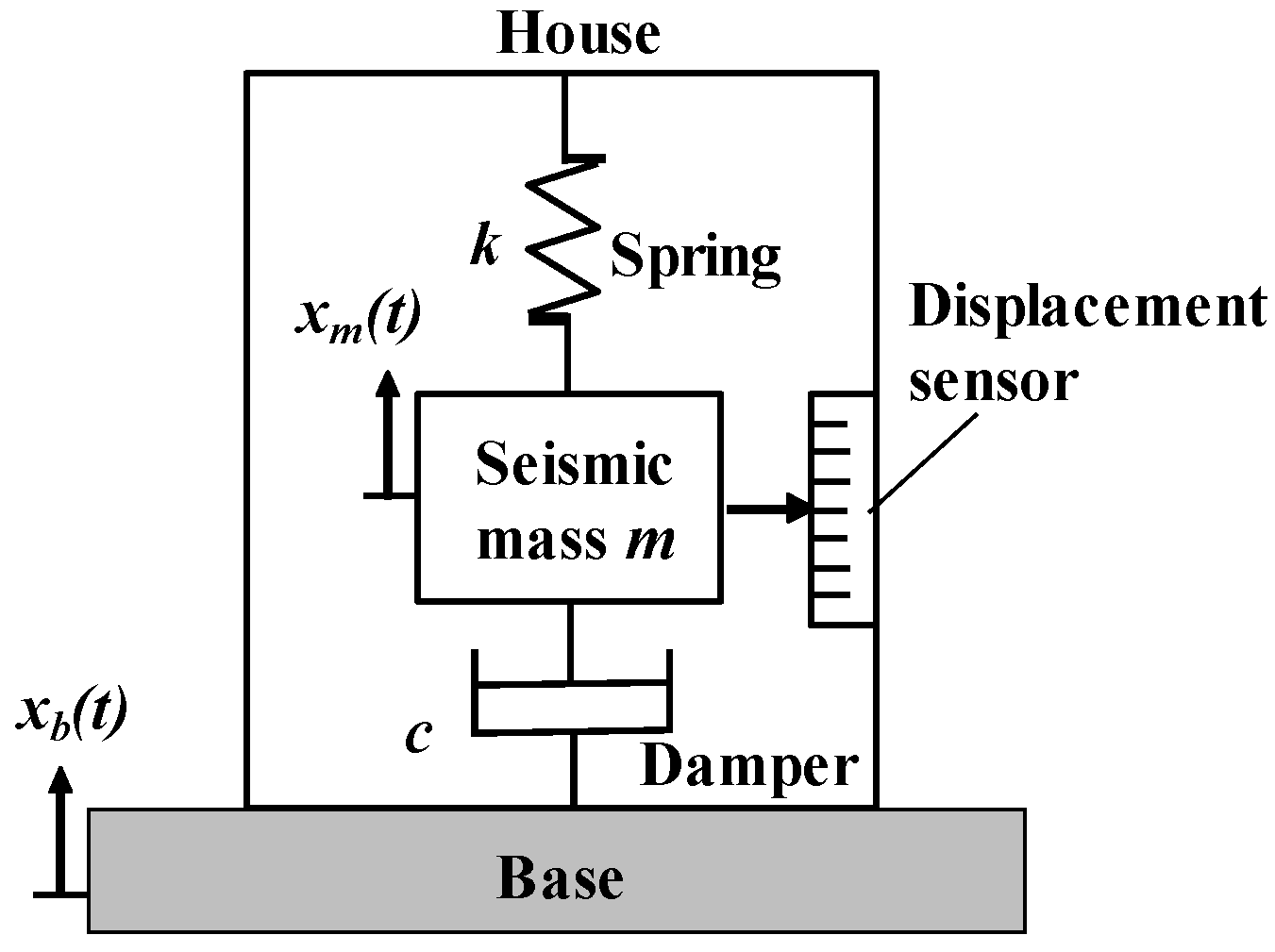
A common accelerometer comprises a spring, a damper, a seismic mass, and a displacement sensor arranged within a housing attached to a base [1], as shown in Figure 1. In operation, the base is mounted on the vibrating structure to be measured, and the relative displacement between the seismic mass and the base is recorded by the displacement sensor.
Figure 1. Typical accelerometer structure diagram.
Following Newton’s second law, the force acting on the seismic mass m can be expressed as
where xm is the displacement of the seismic mass, xb is the displacement of the base, a is the acceleration to be detected, k is the elastic coefficient of spring, and c is the damper coefficient of the accelerometer. The relative displacement z between the seismic mass and the base can be expressed as
Assuming the detected vibration is a simple harmonic vibration, we have xb(t) = Xb cos(ωbt), where ωb is the frequency of vibration. Bring xb(t) and z(t) into Equation (1):
Solve Equation (3) and obtain:
where ωn = (k/m)1/2 is the resonant frequency of the accelerometer, ξ = c/2(mωn) is the damping ratio of the accelerometer, and φ can be expressed as
Additionally, the acceleration caused by vibration is
Equation (4) can be rewritten as
Order
When ωb ≪ ωn, the H(ωb/ωn) ≈ 1 and φ ≈ 0. Then the acceleration value x¨b
can be calculated as
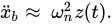
As can be seen from Equation (9), the mechanical sensitivity of the accelerometer can be approximated as the inverse of the square of its resonant frequency, so the higher the resonant frequency, the lower the mechanical sensitivity. Therefore, the low frequency accelerometer needs to have a lower resonant frequency. Additionally, the use of high-sensitivity displacement sensors can also improve the sensitivity of accelerometers.
2. Requirements of Low Frequency Accelerometers
Low-frequency, high-sensitivity accelerometers have a wide range of applications, and they play an important role in industries and daily life, including inertial navigation, structural health monitoring, active vibration isolation systems, fault detection of wind turbine, and earthquake detection.
2.1. Inertial Navigation
Navigation techniques are divided into two categories: positioning and trajectory extrapolation [2]. One representative of positioning technology is a global navigation satellite system. The trajectory extrapolation method recursively measures the amount of variation in the real-time motion state of a moving object relative to the initial motion state. Then, the real-time position of the moving object based on that amount of change is determined. Inertial navigation is an example of the trajectory extrapolation method used as a navigation technique. An accelerometer in an inertial navigation system can measure the acceleration and angular acceleration of the carrier. In accordance with Newton’s second law of motion, time integrates acceleration and angular acceleration to obtain the velocity, angular velocity, and position information of a moving object. The operation of time integration will amplify the error of the accelerometer, and thus, an accelerometer used in an inertial navigation system must meet high accuracy, stability, and anti-interference capability requirements. Optical accelerometers exhibit advantages in terms of accuracy, stability, and immunity to electromagnetic interference by utilizing optical sensing. They demonstrate good prospects in inertial navigation.
2.2. Structural Health Monitoring
Bridges vibrate when vehicles pass over them, and high buildings sway when strong winds blow around them. If the vibration of large buildings exceeds the threshold value, catastrophic losses may occur. Accelerometers can measure the structural vibration of these buildings to determine their structural health and provide early warning for potential damage. Structural vibrations in large buildings are typically low-frequency vibrations below 100 Hz, and they require a multipoint arrangement for monitoring. Therefore, accelerometers must achieve high accuracy with a small size and meet the requirements for long-distance measurement [3]. An optical sensor-based accelerometer has high measurement accuracy while enabling long-distance and distributed measurements; thus, it can meet the structural health monitoring needs of large buildings [4].
2.3. Vibration Isolation Systems
In microscale and nanoscale precision measurement systems and ultra-precision machining systems, the effects of vibration on measurement precision and machining accuracy is devastating, and the vibration is a major factor that limits the improvement of measurement and machining accuracy [5][6]. Vibration isolation is divided into active and passive vibration isolations; passive vibration isolation techniques experience difficulty in isolating low-frequency vibrations of 0.5–5 Hz [7], while active vibration isolation can suppress low-frequency vibrations more efficiently. In an active vibration control system, accurate access to real-time vibration information is the key. Therefore, high-precision real-time detection of low-frequency micro-vibrations must be inevitably achieved. Optical accelerometers demonstrate advantages in measurement accuracy and response speed. They have potential applications in the field of precision active vibration isolation.
2.4. Fault Detection of Wind Turbine
Wind energy has grown rapidly in the last decade due to its clean and renewable nature. By the end of 2021, more than 650 GW of installed wind energy capacity has been put into operation worldwide. Mechanical drive components (gears and bearings) of wind turbines are prone to failure due to exposure to harsh environments, such as random winds, temperature differences, and alternating loads [8][9][10]. Mechanical failures of wind turbines may lead to their shutdown and have adverse social impacts. Therefore, the study of mechanical failure detection of wind turbine units has received increasing attention develop a reasonable operation and maintenance plan and to avoid catastrophic consequences. The lowest rotational frequency of the internal rotating mechanism of a wind turbine can be as low as 0.33 Hz [11], so the fault detection accelerometer of a wind turbine needs to have good low-frequency response characteristics, as well as high sensitivity.
2.5. Earthquake Monitoring
Advances in seismology have relied closely on the development of instruments. From a scientific point of view, accuracy is crucial: the more accurate the detection of seismic properties, the more reliable the understanding of earthquake hazards, which in turn is of guiding importance for the study of seismic prevention techniques. In addition to seismic research, monitoring of earthquakes is also used in resource exploration, gravity-assisted navigation, and monitoring of volcanic activity. According to previous studies, the frequency range of the Earth’s near-source strong ground motions is 0.3–3.0 Hz [12]; therefore, earthquake monitoring accelerometers need to have good low-frequency response characteristics.
This entry is adapted from the peer-reviewed paper 10.3390/app12083994
References
- Venkateshan, S.P. Mechanical Measurements; Springer: New York, NY, USA, 2015.
- Noureldin, A.; Karamat, T.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013.
- Antunes, P.; Lima, H.; Alberto, N.; Rodrigues, H.; Pinto, P.; Pinto, J.; Nogueira, R.; Varum, H.; Costa, A.; Andre, P. Optical fiber accelerometer system for structural dynamic monitoring. IEEE Sens. J. 2009, 9, 1347–1354.
- Guo, T.; Shao, L.; Tam, H.; Krug, P.; Albert, J. Tilted fiber grating accelerometer incorporating an abrupt biconical taper for cladding to core recoupling. Opt. Express 2009, 17, 20651–20660.
- Rivin, E. Vibration isolation of precision equipment. Precis. Eng. 1995, 17, 41–56.
- DeBra, D. Vibration isolation of precision machine tools and instruments. CIRP Ann. 1992, 41, 711–718.
- Liu, J.; He, J. Research on measurement of low-frequency and micro-amplitude of vibration in active damping of platform. J. Univ. Shanghai Sci. Technol. 2005, 27, 185–188. (In Chinese)
- Salameh, J.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Processing 2018, 111, 251–264.
- Amirat, Y.; Benbouzid, M.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636.
- Igba, J.; Alemzadeh, K.; Durugbo, C.; Henningsen, K. Performance assessment of wind turbine gearboxes using in-service data: Current approaches and future trends. Renew. Sustain. Energy Rev. 2015, 50, 144–159.
- Teng, W.; Ding, X.; Tang, S.; Xu, J.; Shi, B.; Liu, Y. Vibration analysis for fault detection of wind turbine drivetrains—A comprehensive investigation. Sensors 2021, 21, 1686.
- Clinton, J.; Heaton, T. Potential advantages of a strong-motion velocity meter over a strong-motion accelerometer. Seismol. Res. Lett. 2002, 73, 332–342.
This entry is offline, you can click here to edit this entry!
