If we were to sort chemical reactions by their importance for life, electron transfer (ET) would be the best candidate to be ranked first. The reasons for its importance lie in the key role it carries out in major biological processes, such as the electron transport chain and photosynthesis, as well as artificial processes, such as information storage (i.e., photography) and energy conversion (batteries). It is worth noting that ET is ubiquitous in all the branches of chemistry, from organic and biochemistry to physical and inorganic chemistry. The systematic study of the ET processes can be fundamental both for basic knowledge and for strongly applicative reasons.
1. Multicomponent Systems: Supramolecular vs. Molecular Entities
In his Nobel lecture of 1988 [
35], Jean-Marie Lehn gave the definition of supramolecular chemistry, describing a supramolecular structure as the association of two or more chemical species held together by intermolecular forces. Starting from such a definition, multicomponent photophysical devices in which the components are held together by covalent interactions, such as the D-B-A systems, have a clear molecular nature. However, in the literature, there are plenty of papers describing this kind of structure [
1] and cataloging them as supramolecular systems. The reasons for such an apparent misconception come from the existence of some features, proper supramolecular structures, which can be adopted by the D-B-A devices if designed in the correct way. In supramolecular architectures, the molecules are spatially organized to forge assembled systems able to show new features while maintaining the properties of the single components. Such peculiarities can also be found in multicomponent systems held together by covalent bonds, which can be defined as structurally molecular/covalent and functionally supramolecular [
36]. The supramolecular feature discussed above constitutes a key aspect in the design of a working D-B-A device, in which it is mandatory to maintain the properties of the single components in the final assembled system in order to predict the behavior of the device in the design phase. Practically, the covalent connections have to guarantee a reduced electronic coupling between the subunits.
2. Photoinduced Charge Separation, Charge Recombination, and the Superexchange Mechanism
The choice of the correct building blocks and the ways to connect them is not only obviously essential to producing an operative D-B-A device, but it also determines the mechanism determining the photoinduced electron transfer happens. The photoinduced electron transfer can be oxidative, where the excitation of the D subunit leads to the transfer of an electron to the LUMO of the acceptor (Equations (1) and (2)), or reductive, where it is the excited state of the acceptor that provides the driving force for the electron transfer from the donor to the HOMO of the acceptor (Equations (3) and (4)).
The “supramolecular” identity of these systems allows one to thermodynamically estimate the driving force of both PET and charge recombination by exploiting the redox data of the single components. The Gibbs free energy in standard conditions and in an oxidative electron transfer pathway (similar treatment is possible to do for the reductive ET), assuming the validity of Koopman’s theorem [
37], is expressed in Equation (5) as follows:
where the term *
Eox is the oxidation potential of the excited state of the donor chromophore,
Ered is the first reduction potential of the acceptor,
e is the charge of the electron, and
W represents the work term, which is the difference between Coulombic stabilization energy of reactants and products, normally neglected in D-B-A systems [
38,
39]. In Equation (5), the term
e*
Eox is described by the following equation:
In Equation (6), the term
E0−0 is the excited state energy and can be estimated from photophysical data; in particular, it corresponds to the emission maximum of the donor recorded at 77 K [
16,
40,
41,
42]. Whereas the thermodynamics of the system depends on the electrochemical properties of both the donor and acceptor systems, the predictability of the PET reaction rate appears much more complicated.
The rate constant of an ET reaction can be expressed by using Equation (7) as follows:
The
HET term indicates the electronic coupling between reactants and products in the electron transfer reaction (which will be extensively discussed later). The
FCWD is the Franck–Condon weighted density of states [
43,
44,
45,
46,
47,
48], a nuclear term that takes into account the overlap between the vibrational wavefunctions belonging to the products and reagents. Such a factor can be expressed in a single-mode approximation with a quantum mode of frequency
υi [
49] as follows:
where
S is the Huang–Rhys factor
S=λihυi,
λi represents the inner-sphere reorganization energy and
λ0 represents the outer-sphere reorganization energy [
48]. The
FCWD term can be simplified at a high-temperature limit by using the following equation:
where
λ=(λ0+λi). Although the
FCWD term is important for the predictability of the rate constant of an ET process, the electronic coupling term
HET is more influenced by the nature of the bridge. The electronic term can assume different expressions depending on which mechanism is followed to obtain the electron transfer. Both oxidative and reductive PET can happen through a superexchange or incoherent charge transport (hopping) mechanism, where the latter is less common in D-B-A systems. The superexchange model works by assuming that the HOMO and LUMO of the bridge are energetically far apart from those of the D and A systems. In these conditions, bridge orbitals are involved in the formation of virtual states that electronically connect D and A subunits, according to the McConnell superexchange model [
50]. Since the virtual states involved in the PET mechanism are different considering oxidative or reductive pathways, they will be discussed separately.
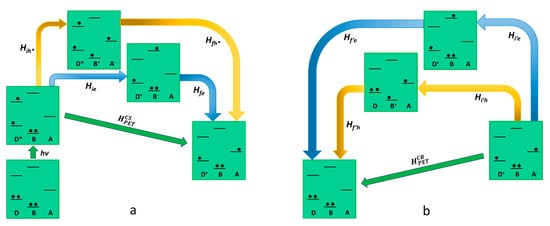
As far as the
Oxidative photoinduced electron transfer process is concerned, the relevant electronic states involved (real and virtual) in the oxidative PET are represented in
Figure 2. The initial state, where the donor is electronically excited, is coupled to the final charge-separated state through the following two possible virtual states: (i) the first concerns a virtual mono reduction of the bridge by the excited state of the donor, which assumes a positive charge (D
+-B
−-A); (ii) the second is made by the mono-electron-reduced acceptor, which take an electron from the bridge (D*-B
+-A
−). The superexchange electronic coupling matrix element for the oxidative PET process can be defined as follows:
Figure 2. Schematic representation of oxidative photoinduced electron transfer in D-B-A dyads, according to superexchange. The states involved in the mechanism (virtual states pathways are described with blue and yellow arrows) are represented in terms of electronic configurations. On the left (a) (photoinduced) charge separation is described while charge recombination is shown on the right (b).
In Equation (10), all the Hamiltonian terms concern the electronic coupling between the real and the virtual state, as represented in
Figure 2. The terms
ΔEe and
ΔEh∗ represent the energy difference between the virtual state and the initial/final state for the electron and hole transfer, respectively (the energy of the initial and final state is equivalent as it refers to the transition state geometry). Considering Equation (10) for the case exemplified in
Figure 2, the hole transfer mechanism (the second term of the sum), involving a higher energy virtual state, would be negligible. In light of this, in oxidative photoinduced electron transfer, the ET mechanism for the generation of the charge-separated state is usually the dominant one, and Equation (10) could be reported as
HCSPET=HieHfeΔEe. On the other hand, the charge recombination mechanism involves different virtual states compared to the ones involved in the forward photoinduced path since its final state does not coincide with the initial state of the charge separation. This means that in the electronic coupling matrix element for the charge recombination (
HCRPET in Equation (11)), both terms of the sum are valid to describe a possible pathway.
Summing up, the only virtual state involved in the charge separation is the D+-B−-A, where the bridge is virtually mono-reduced, meanwhile, the possible virtual states in the charge recombination are D+-B−-A and D-B+-A−. We can conclude that in the design of a D-B-A system finalized to reach a long-lived charge-separated state via oxidative photoinduced electron transfer, it would be better to avoid the use of easy-to-oxidize bridge subunits. Such a kind of bridge would speed up the charge recombination without playing any effect on the charge separation.
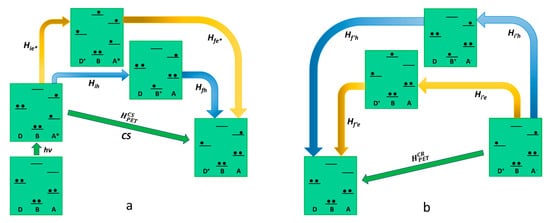
As far as
reductive photoinduced electron transfer is concerned, also, in this case, there are two possible pathways that lead to charge separation with two virtual states involved, as described in
Figure 3. One path contemplates the virtual state D-B
+-A
−, in which the excited state of the acceptor receives an electron from the bridge. The other virtual state is a D
+-B
−-A*, in which an electron is transferred from the ground state of the donor to the bridge. So, the superexchange electronic coupling matrix element for the reductive PET process can be expressed as follows:
Figure 3. Schematic representation of reductive photoinduced electron transfer in D-B-A dyads, according to superexchange. The states involved in the mechanism (virtual states pathways are described with blue and yellow arrows) are represented in terms of electronic configurations. On the left (a) charge separation is described while charge recombination is shown on the right (b).
Different from the oxidative PET, in reductive PET, it is the first term of Equation (12) that can be neglected, so the dominant pathway is the one that includes the D-B
+-A
− virtual state, allowing us to present the Equation (12) in a simplified version
HCSPET=HihHfhΔEh. The charge recombination mechanism in the reductive PET, connecting the D
+-B-A
− charge-separated state and the D-B-A ground state, provides two different pathways involving as many virtual states, the electron transfer D
+-B
−-A and the hole transfer D-B
+-A
−. In this case, the electronic coupling matrix element for the charge recombination is formally equivalent to the one related to the oxidative PET as follows:
As it results clearly, in the case of reductive PET, the conclusions are the opposite if compared to the oxidative mechanism. In this case, in fact, the only virtual state involved in the charge separation (D-B+-A−) shows an oxidized bridge, whereas both the possible virtual states (D+-B−-A and D-B+-A−) are accessible in the charge recombination step. We can conclude that in the design of this kind of device for a reductive PET, an easily reducible bridge should not be taken into consideration to avoid the acceleration of the charge recombination without producing the same effect in the charge separation step.
This entry is adapted from the peer-reviewed paper 10.3390/molecules27092713