Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Bone is an outstanding, well-designed composite. It is constituted by a multi-level structure wherein its properties and behavior are dependent on its composition and structural organization at different length scales. The combination of unique mechanical properties with adaptive and self-healing abilities makes bone an innovative model for the future design of synthetic biomimetic composites with improved performance in bone repair and regeneration.
- bone
- composite
- material
1. Nanostructure
Bone is composed of a weight fraction range of 65–70% inorganic component, 18–25% organic, and 10−12% water, whereas on a volume fraction range, the proportions for each component are between 33 and 43%, 32 and 44%, and 15 and 25%, respectively [1]. It should be noted that this ratio can vary depending on the age and health conditions of the human being [2].
The organic phase of bone composite consists primarily of type I collagen (90% by weight), some other minor collagen types (III and VI), and a variety of non-collagenous proteins such as laminin, fibronectin, vitronectin, osteocalcin, osteonectin, osteopontin, and bone sialoprotein [3]. The basic structural unit of collagen is called tropocollagen (see Figure 1), which is a very rigid linear molecule with a diameter and length of 1.1 nm and 300 nm, respectively [4]. This molecule possesses a rearranged, right-handed, triple-helix structure formed by polypeptide chains with a highly repetitive amino acid sequence, glycine-X-Y, where glycine is being used in every third residue and X is often proline and Y is frequently hydroxyproline [5][6]. This frequent occurrence of proline and hydroxyproline stabilizes the polypeptide strands (e.g., through interchain hydrogen bonds) and limits rotations, leading to its tightly packed triple-helical form [7]. The triple-helix structures are associated with microfibrils, where five tropocollagens are assembled in parallel (D-period) [5]. At the next level of the hierarchy, the tropocollagen molecules congregate into fibrils by being covalently cross-linked at their tips and their axial staggering, forming overlap zones and gaps with a specific periodicity of approximately 67 nm [4][7].

Figure 1. Representation of the collagen fibers’ structural organization. The type I collagen major amino acid components Gly-Pro-HyPro constituting the α chains are self-assembled in a triple-helix, tropocollagen structure. Stacks of mineral crystals lie between the congregated tropocollagen molecules to form mineralized collagen fibrils with a characteristic D-period. These fibril molecules are then packaged to form collagen fibers [8][9][10][11].
The inorganic phase of bone is a ceramic crystalline-type mineral, as an impure form of naturally occurring calcium phosphate, most often referred to as biological non-stoichiometric hydroxyapatite. Bone hydroxyapatite is not pure hydroxyapatite, because the tiny apatite crystals contain impurities such as potassium, magnesium, strontium, sodium (in place of the calcium ions), carbonate (4 to 6% of the phosphate groups are replaced by carbonate groups), and chloride or fluoride (in place of the hydroxyl ions). These impurities reduce the crystallinity of the apatite and consequently alter some properties, such as solubility, which is crucial for mineral homeostasis and bone adaptation. There is a long ongoing debate about the nature of the mineral particle shape—needles versus platelets [12][13][14]. More recently, the existence of mineral particles with a fractal aggregate shape was also discovered [15].
At the submicron scale, bone is composed of building blocks of mainly type I collagen, mineral crystals, water, and non-collagenous proteins [16]. The organic and inorganic components of bone blend together to generate mineralized collagen fibrils, as demonstrated in Figure 1. The mineral component in bone occurs as stacks of thin polycrystalline sheets, which surround and lie between the collagen fibrils [4]. The collagen–mineral system is arranged in parallel arrays within thin sheets called lamellae. As stated previously, the organization of the lamellae differs between cortical and trabecular bone. As identified by Fratzl et al. [17], the lamellae are assembled in a “rotated plywood-like fashion” in cortical bone. In cancellous bone and according to Chen et al. [18], these structures are strongly fused, forming a sheet-like structure.
The mechanical properties of the organic and inorganic phases together with their hierarchical arrangement confer bone features that determine its characteristic strength and toughness [19]. The mineral content predominantly contributes to bone stiffness and strength. Therefore, when the organic collagen in bone is removed—by heat or leach—mature bone becomes brittle [17][18][20]. Based on a computational study [19] where nanoindentation data were considered, single hydroxyapatite crystals demonstrated stiffness values of 150 GPa and 143 GPa in the [0001] and [1010] direction, respectively. In a more recent study, Pang et al. [21] identified the presence of an organic substance binding the mineral components together, and the authors believe that it contributes to the strength, stiffness, and energy absorption of bone under compression. In a thorough study [16], Wang and Ural demonstrated that the increase in the elastic modulus, ultimate strength, and fracture energy of the mineralized collagen fibrils networks was significantly influenced by both the increased uniformity of mineral distribution and stronger interactions between the components and was modestly influenced by the rise in total volume fraction of minerals. This research also concluded that the mineral distribution had the most drastic influence on the elastic modulus compared to the ultimate strength and fracture energy. However, bone strength does not depend solely on bone mineral distribution, but also on the quality and material properties of the organic component where collagen cross-links play an important role in the reinforcement of bone strength [22]. Significant determinants of the functional integrity of the organic phase are the degree and nature of enzymatic lysyl oxidase-mediated collagen crosslinks and the negative effects of non-enzymatic glycation-induced collagen crosslink (the production of advanced glycation end-products such as pentosidine), which can be considered in a competitive relationship with enzyme-derived cross-linking [23][24]. Enzymatic cross-linking density has been related to governing post-yield and large-scale mechanics, and cross-link strength governs failure strain, hence improving fracture toughness, bone strength, and stiffness [25][26][27]. Meanwhile, non-enzymatic cross-linking is related to the prevention of energy absorption by microdamage formations, reducing bone toughness and ultimate strain [28][29] and accelerating brittle fracturing [30][31].
Mineralized collagen fibrils are embedded in an extrafibrillar matrix that consists of water, mineral, and non-collagenous proteins [29]. A recent study [1] used positron annihilation lifetime spectroscopy (PALS), a technique sensible to voids/pores at the nanometer and subnanometer scale, to observe these structures. It was noticed that water mainly occupies the regions in intercollagen molecular spaces, terminal segments (D-spacing) within collagen microfibrils, and interface spacing between collagen and mineral structures. Water was also identified as being loosely bound to the surfaces of collagen fibrils [4]. The bone water content is an essential component since it confers much of bone’s unique strength and resilience by stress reduction during dynamic loading [32][33]. Hence, removing bound water in the bone matrix makes bone stiffer, stronger, but more brittle at different length scales, because dry collagen loses its deformation and energy absorption capacity [34]. As stated by Leo et al. [5], the lack of collagen external water promotes the formation not only of new inter-tropocollagen hydrogen bonds but also of intra-tropocollagen ones, which cause the microfibril gain of compactness and tubularity. These molecular and supramolecular changes are responsible for the generation of very large stresses up to 100 MPa when the collagen undergoes complete dehydration [35]. Bone mechanical properties are not only intimately linked to its nanostructure composition but also to its organization, where further study and profound understanding are still needed.
2. Microstructure
There are two types of bone tissues: primary or woven bone, present in newly developed immature bone at fracture site callus, and lamellar bone, which is the more mature form of bone, found in the adult human skeleton. In cortical bone, lamellar bone can be found as extended parallel arrays called circumferential lamellae and also as smaller lamellae cylindrical structure arrangements, called osteon (or the Haversian system). Each osteon consists of about 10 to 30 lamellae arranged in concentric cylinders built up around the neurovascular channel, called the Haversian canal (see Figure 2). The outer surface of the osteon constituted by a thin layer of calcified mucopolysaccharides, the cement line, is the weaker cracking path, leading to crack deflection. Cancellous bone consists primarily of lamellae, arranged in a less organized lattice-like network of matrix spikes, called trabeculae, to form a network of rods and plates, which on average have a thickness in the range of 100–200 μm. Trabeculae are interspersed with large bone spaces (in the order of 500 to 1500 μm) filled with bone marrow [36][37][38]. Unlike the elastic properties, the post-yield properties and failure mechanisms of bone under compression differ significantly at the two length scales. Schwiedrzik et al. [39] demonstrated that isolated bone lamellae show high strength and ductility but no damage and fail mostly by the development of shear planes, while the response of macroscopic specimens containing numerous osteons is quasi-brittle with low strength and ductility, presenting substantial damage and longitudinal cracks.
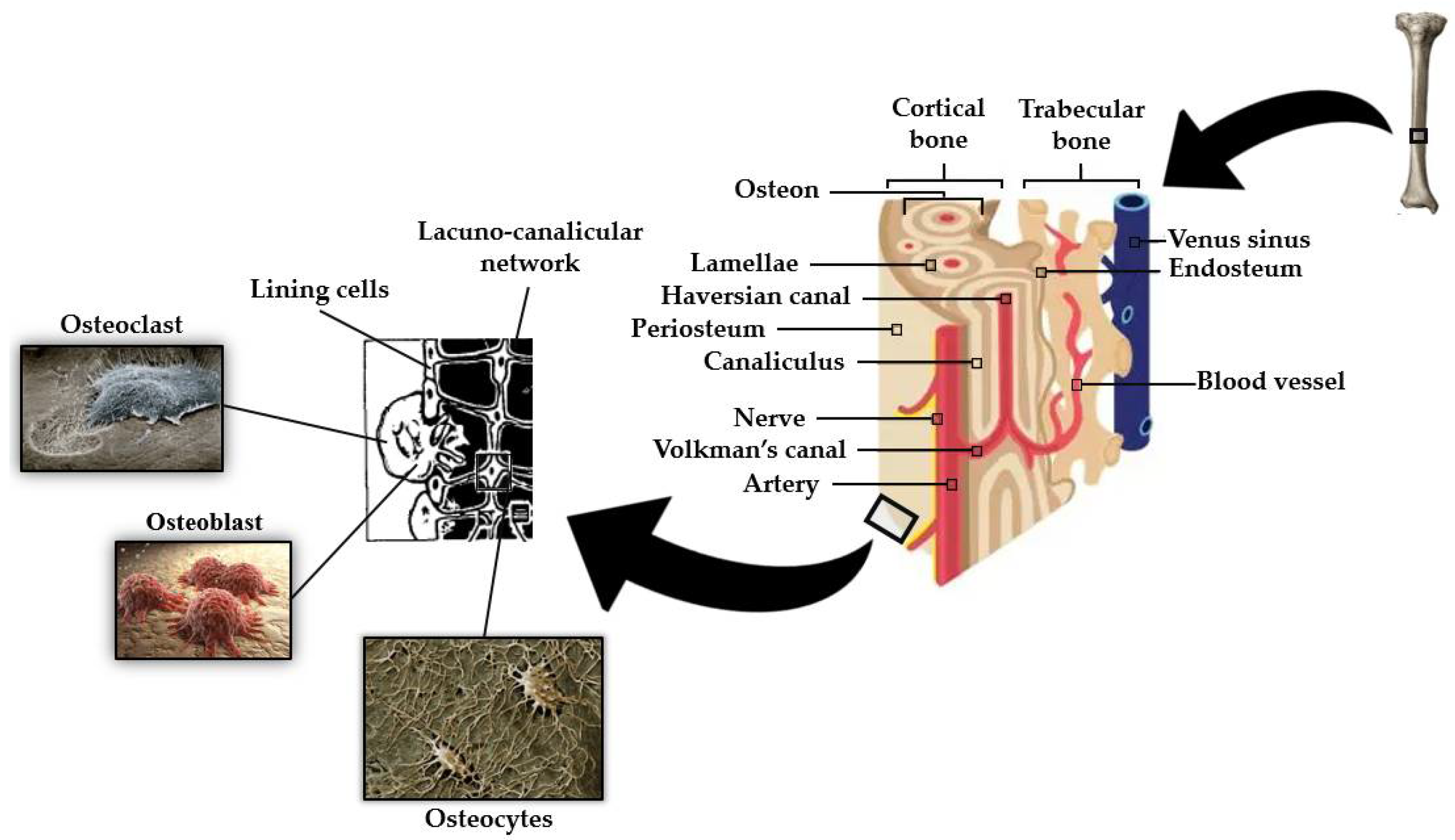
An outstanding feature of bone is the fact that its mass is maintained by and adapted to mechanical strain [45]. This mechanotransduction process is a well-orchestrated cellular event regulated by complex interactions between the various cell types found in bone, primarily osteoblasts, osteoclasts, and osteocytes (see Figure 2) [46].
Osteocytes have become generally accepted as the mechanosensory cells within the bone [45]. The mechanosensation and mechanotransduction mechanisms in osteocytes arise from their unique stellate shape and interconnected architecture. An osteocyte is made up of an ellipsoid cell body that occupies a fluid-filled space within its lacunae. Osteocytes are interconnected by many long dendritic processes that pass through a network of small channels called canaliculi (as can be seen in Figure 2) [47][48]. The process of converting external mechanical forces into biochemical responses, known as mechanotransduction [45], includes the response of the osteocyte to the cell direct mechanical deformation/strain as a consequence of bone matrix strain [49], to shear stress due to load-induced fluid flow [50], to electric fields caused by stress-generated streaming potentials [51], and to hydrostatic pressure [52]. Recent mechano-regulatory in vitro and in silico bone tissue engineering experiments [53] point towards the determinant influence of low shear strain and fluid velocity in bone adaptive response and cell differentiation. Despite the mechanism of stimuli perception in osteocytes not being fully understood, both cell bodies (e.g., osteocytes plasma membrane disruptions) [54] and dendritic processes [55][56] have been proven to perceive mechanical forces applied to the bone. Kola et al. [48] demonstrated that lacunar strain value increased as lacunae size increased, with the highest strain magnification ratio observed for horizontally aligned lacunae. The authors also demonstrated the influence of the perilacunar region modulus in the strain magnification generated at the lacuna. Variations in lacunar morphology such as an increase in lacuna sphericity cause changes in the mechanical environment of osteocytes, in particular a decrease in maximum effective local strains [57].
In addition to their hosting-site and sensorial stimuli mechanisms for osteocytes, lacunae have a structural role in the local mechanical properties and fracture behavior of the bone matrix. In a finite element study developed by Hamed and Jasiuk [58], the apparent elastic modulus of the bone matrix was lowered by the existence of osteocyte lacunae. Kaya et al. [59] verified that bone elastic modulus changes were related to cumulative increases in void volume in lacunae and canaliculi, which were induced by rat models’ lactation and recovery stages. More recently, Sang et al. [60] demonstrated a significant linear relation between the physiological range of osteocyte lacunar porosity area, density, size, and orientation and the elastic modulus and ultimate strength of the bone matrix in virgin and lactation rats. The influence of osteocyte lacunae structure on crack initiation and propagation has also been studied. Lacunae voids create bands of stress concentrations as a result of high local strains around osteocytes, providing a site for crack nucleation [61]. According to Josephson et al. [62], despite the number of lacunae damage initiation sites and the rate of crack growth, perilacunar regions can delay or prevent the emergence and growth of microcracks. In the study developed by Sang et al. [60], osteocyte lacunae demonstrated a guiding effect on the cracks, i.e., attracted a nearby crack due to stress concentrations near lacunar boundaries. The authors also inferred that a reduced density of osteocyte lacunae may also lead to regions where the crack may grow more easily, which may have an adverse impact on bone fragility fractures. There was no relation between the energy dissipated during damage and crack formation, a measure of fracture resistance, and the osteocyte lacunae structural parameters.
After sensing mechanical loads applied to the bone, osteocytes react by controlling osteoblast and osteoclast activities through cell-to-cell communication and via secreted factors [63]. Osteocytes connect to cells on the bone surface and the vasculature by many long dendritic cytoplasmic processes ranging from 40 to 100 per cell [64]. Osteocytes and osteoblasts communicate with one another through gap junctions present on the tips of the cell processes. These are bidirectionally transmembranar channels that connect the cytoplasm of two adjacent cells and regulate the passage of molecules less than 1 kDa [64].
Osteoblasts are secretory cells, responsible for the formation of the pre-mineralized bone matrix, called osteoid, predominantly comprising bony matrix proteins such as type I collagen and trace quantities of type V collagen, and also other non-collagenous proteins such as osteopontin, osteocalcin, osteonectin, osteoprotegerin, bone morphogenetic proteins, and glycoproteins. The mineralization process of osteoid involves the supersaturation of extracellular fluids at local zones and increased osteoblastic alkaline phosphatase activity, which raises local calcium and phosphate concentrations. Osteoblasts produce osteocalcin protein, which binds calcium and further concentrates local calcium levels [32][65][66][67][68].
During the process of bone formation, some osteoblasts, involved in the production of bone matrix, become embedded in that matrix. The fundamental question of how osteoblasts are buried remains largely unanswered. The matrix around a newly incorporated cell is not yet calcified (osteoid) but gradually calcifies as the formation front moves away because of continuing osteoblastic activity. Osteoid osteocytes still possess many features of the original osteoblast, and their major functions are to simultaneously: (i) regulate mineralization because they are not as active as osteoblasts in the generation of a mineralized matrix, (ii) reduce the number of organelles and cytoplasmic volume, and (iii) gain the long connective slender cell processes [32][69][70].
Osteoclasts are irregularly shaped giant cells (15 to 20 μm or more) that originate from monocytes and macrophages (two types of white blood cells). They are specialized in the local removal of bone during growth and during the remodeling of osteons and bone surfaces. These cells are found in depressions called Howship’s lacunae or resorption bays. For bone resorption to occur, osteoclasts have an interface known as the “ruffled brush” border, formed by a highly enfolded plasma membrane, which increases the surface area. The “ruffled brush” border is surrounded by a clear zone, as well as a well-defined zone of actin filaments responsible for bone resorption. Osteoclasts bind to bone surfaces via anchoring proteins such as integrins and create a seal and lower the pH by releasing protons (e.g., hydrogen ions via carbonic anhydrase) and by expressing acid hydrolases (e.g., tartrate-resistant acid phosphate). This environment is suited to increase the solubility of hydroxyapatite crystals as well as destroy the organic matrix with lysosomal (cathepsin K) and non-lysosomal (collagenase) enzymes. The osteoclastic bone resorption is inhibited by calcitonin and interleukin-10 and stimulated by osteoblast-derived signals, cytokines from cells, including macrophages and lymphocytes (e.g., interleukin-1), and blood-circulating factors (e.g., parathyroid hormone) (see Figure 3) [32][65].
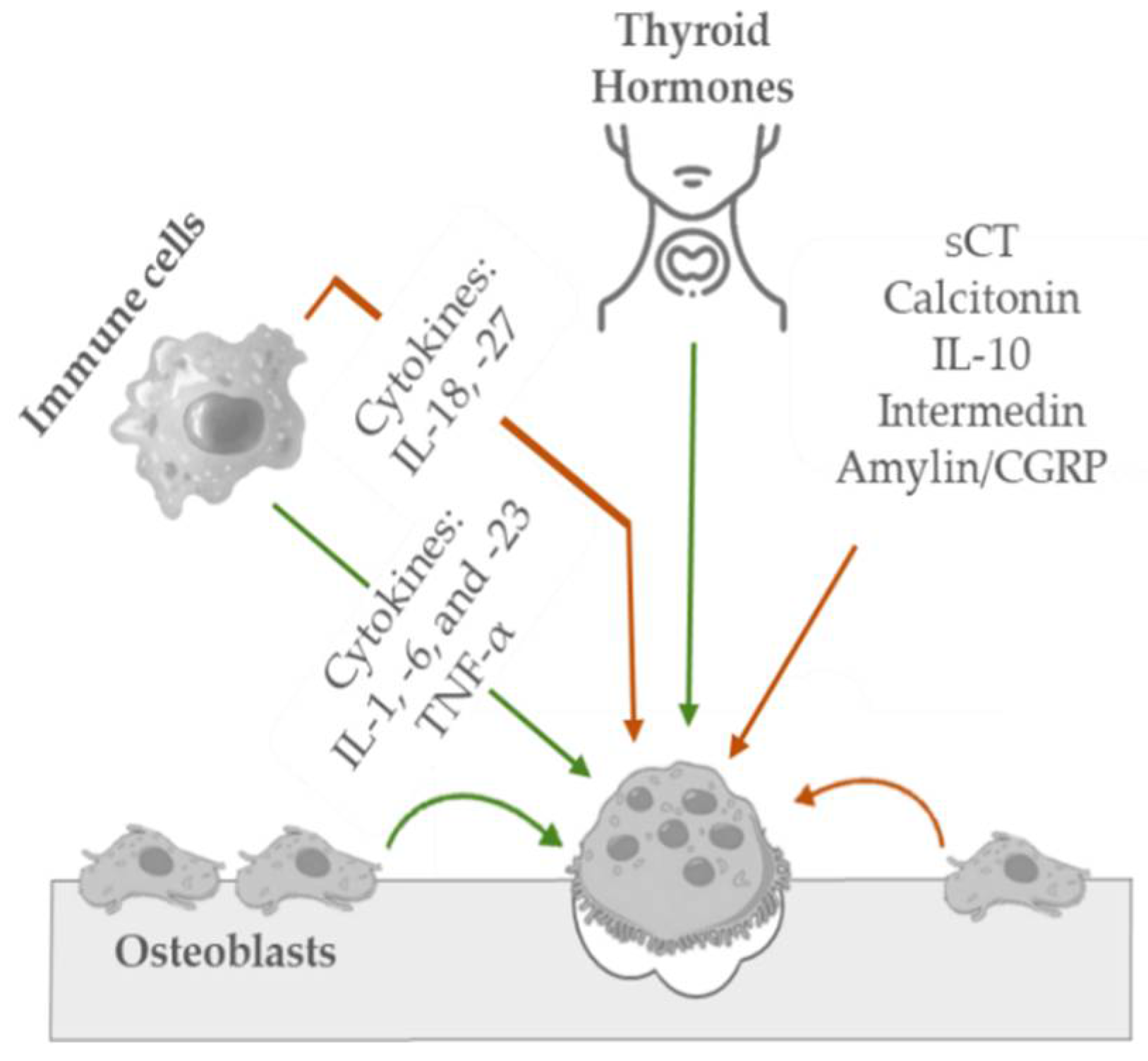
Figure 3. Schematic representation of the key mediators in osteoclastic bone inhibition (orange arrow) and stimulation (green arrow) mechanisms.
Hence, throughout life and in response to mechanical and physiological stimuli, bones suffer growth and processes of shaping and reshaping by independent actions of osteoblasts and osteoclasts (a process known as bone modeling) and are subjected to continuous and dynamic equilibrium (bone resorption and formation), responsible for preserving its functional integrity (a process known as bone remodeling) [46][63]. Despite the complexity of the rules that govern the effects of bone mechanical loading on cells and tissue differentiation, growth, adaptation, and maintenance, research efforts are being applied to try to describe and understand these complex phenomena through the challenging task of developing microscale mechanobiology computational models. Numerical methods, such as finite element simulation, are being considered for the development of these models by integrating the contributions of applied external mechanical loads, cellular activities, and cellular nutrients, such as oxygen and glucose supply [71], the incorporation of biochemical osteocyte feedback [72], angiogenesis [73], and the autocrine and paracrine signaling pathways of bone cells [74]. Once the mechanisms of mechanically regulated bone response are better understood, physiological conditions and pharmacological agents may be developed to promote better and faster bone tissue repair and formation [75].
This entry is adapted from the peer-reviewed paper 10.3390/app12073381
References
- Ahn, T.; Gidley, D.W.; Thornton, A.W.; Wong-Foy, A.G.; Orr, B.G.; Kozloff, K.M.; Banaszak Holl, M.M. Hierarchical Nature of Nanoscale Porosity in Bone Revealed by Positron Annihilation Lifetime Spectroscopy. ACS nano 2021, 15, 4321–4334.
- Pai, S.; Kwon, J.; Liang, B.; Cho, H.; Soghrati, S. Finite element analysis of the impact of bone nanostructure on its piezoelectric response. Biomech. Model. Mechanobiol. 2021, 20, 1689–1708.
- Shekaran, A.; García, A.J. Extracellular matrix-mimetic adhesive biomaterials for bone repair. J. Biomed. Mater. Res. A 2011, 96, 261–272.
- Törnquist, E.; Gentile, L.; Prévost, S.; Diaz, A.; Olsson, U.; Isaksson, H. Comparison of small-angle neutron and X-ray scattering for studying cortical bone nanostructure. Sci. Rep. 2020, 10, 14552.
- Leo, L.; Bridelli, M.G.; Polverini, E. Reversible processes in collagen dehydration: A molecular dynamics study. Arch. Biochem Biophys 2021, 714, 109079.
- Gordon, M.K.; Hahn, R.A. Collagens. Cell Tissue Res. 2010, 339, 247–257.
- Hillgärtner, M.; Linka, K.; Itskov, M. Worm-like chain model extensions for highly stretched tropocollagen molecules. J. Biomech. 2018, 80, 129–135.
- Liu, Y.; Luo, D.; Wang, T. Hierarchical structures of bone and bioinspired bone tissue engineering. Small 2016, 12, 4611–4632.
- Friedrich, J. Analyzing Interactions between Cells and Extracellular Matrix by Atomic Force Microscopy. Ph.D. Thesis, Technischen Universität Dresden, Dresden, Germany, 2009.
- Gültekin, O. Computational Inelasticity of Fibrous Biological Tissues with a Focus on Viscoelasticity, Damage and Rupture; Verlag der Technischen Universität Graz: Graz, Austria, 2019.
- Van Gulick, L.; Saby, C.; Morjani, H.; Beljebbar, A. Age-related changes in molecular organization of type I collagen in tendon as probed by polarized SHG and Raman microspectroscopy. Sci. Rep. 2019, 9, 7280.
- Fonseca, J.E. Bone: A story of breakthroughs, a promising future. Medicographia 2012, 34, 142–148.
- Keaveny, T.M.; Morgan, E.F.; Yeh, O.C. Bone mechanics. In Standard Handbook of Biomedical Engineering & Design, 1st ed.; Kutz, M., Ed.; McGraw-Hill: New York, NY, USA, 2003; pp. 200–222.
- Morgan, E.F.; Barnes, G.L.; Einhorn, T.A. The bone organ system: Form and function. Osteoporosis 2008, 1, 3–25.
- Reznikov, N.; Bilton, M.; Lari, L.; Stevens, M.M.; Kröger, R. Fractal-like hierarchical organization of bone begins at the nanoscale. Science 2018, 360, eaao2189.
- Wang, Y.; Ural, A. A finite element study evaluating the influence of mineralization distribution and content on the tensile mechanical response of mineralized collagen fibril networks. J. Mech. Behav. Biomed. Mater. 2019, 100, 103361.
- Fratzl, P.; Gupta, H.S.; Paschalis, E.P.; Roschger, P. Structure and mechanical quality of the collagen–mineral nano-composite in bone. J. Mater. Chem. 2004, 14, 2115–2123.
- Chen, P.-Y.; Toroian, D.; Price, P.A.; McKittrick, J. Minerals form a continuum phase in mature cancellous bone. Calcif. Tissue Int. 2011, 88, 351–361.
- Zamiri, A.; De, S. Mechanical properties of hydroxyapatite single crystals from nanoindentation data. J. Mech. Behav. Biomed. Mater. 2011, 4, 146–152.
- White, T.D.; Black, M.T.; Folkens, P.A. Human Osteology, 3rd ed.; Academic Press: Oxford, UK, 2012.
- Pang, S.; Schwarcz, H.P.; Jasiuk, I. Interfacial bonding between mineral platelets in bone and its effect on mechanical properties of bone. J. Mech. Behav. Biomed. Mater. 2021, 113, 104132.
- Barkaoui, A.; Hambli, R.; Tavares, J.M.R. Effect of material and structural factors on fracture behaviour of mineralised collagen microfibril using finite element simulation. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1181–1190.
- Trackman, P.C. Enzymatic and non-enzymatic functions of the lysyl oxidase family in bone. Matrix Biol. 2016, 52, 7–18.
- Garnero, P. The contribution of collagen crosslinks to bone strength. BoneKEy Rep. 2012, 1, 182.
- McNerny, E.M.; Gong, B.; Morris, M.D.; Kohn, D.H. Bone fracture toughness and strength correlate with collagen cross-link maturity in a dose-controlled lathyrism mouse model. J. Bone Miner. Res. 2015, 30, 455–464.
- Depalle, B.; Qin, Z.; Shefelbine, S.J.; Buehler, M.J. Influence of cross-link structure, density and mechanical properties in the mesoscale deformation mechanisms of collagen fibrils. J. Mech. Behav. Biomed. Mater. 2015, 52, 1–13.
- Banse, X.; Sims, T.; Bailey, A. Mechanical properties of adult vertebral cancellous bone: Correlation with collagen intermolecular cross-links. J. Bone Miner. Res. 2002, 17, 1621–1628.
- Siegmund, T.; Allen, M.R.; Burr, D.B. Failure of mineralized collagen fibrils: Modeling the role of collagen cross-linking. J. Biomech. 2008, 41, 1427–1435.
- Siegmund, T.; Allen, M.; Burr, D. A ductile-to-brittle transition in bone failure due to non-enzymatic collagen-crosslinks-A computational study. Trans. Orthop. Res. Soc. 2007, 32, 35.
- Vashishth, D.; Wu, P.; Gibson, G. Age-related loss in bone toughness is explained by non-enzymatic glycation of collagen. Trans. Orthop. Res. Soc. 2004, 29, 497.
- Allen, M.R.; Gineyts, E.; Leeming, D.J.; Burr, D.B.; Delmas, P.D. Bisphosphonates alter trabecular bone collagen cross-linking and isomerization in beagle dog vertebra. Osteoporos. Int. 2008, 19, 329–337.
- Ahn, A.C.; Grodzinsky, A.J. Relevance of collagen piezoelectricity to “Wolff’s Law”: A critical review. Med. Eng. Phys. 2009, 31, 733–741.
- Jilka, R.L.; Noble, B.; Weinstein, R.S. Osteocyte apoptosis. Bone 2013, 54, 264–271.
- Maghsoudi-Ganjeh, M.; Wang, X.; Zeng, X. Computational investigation of the effect of water on the nanomechanical behavior of bone. J. Mech. Behav. Biomed. Mater. 2020, 101, 103454.
- Masic, A.; Bertinetti, L.; Schuetz, R.; Chang, S.-W.; Metzger, T.H.; Buehler, M.J.; Fratzl, P. Osmotic pressure induced tensile forces in tendon collagen. Nat. Commun. 2015, 6, 5942.
- Keaveney, T.M. Cancellous bone. In Handbook of Biomaterial Properties; Black, J., Hastings, G., Eds.; Springer Science & Business Media: Dordrecht, The Netherlands, 2013; pp. 15–23.
- Yoa, H. Mechanical Testing of Bone and Bone-Like Materials Using Image Correlation Strain Measurement Technique; Xi’an Jiaotong University: Xi’an, China, 2007.
- Weld-Moore, R. The Use of Quantitative Ultrasound to Investigate Bone Strength in the Facial Skeleton; Trinity College: Dublin, Ireland, 2018.
- Schwiedrzik, J.; Raghavan, R.; Bürki, A.; LeNader, V.; Wolfram, U.; Michler, J.; Zysset, P. In situ micropillar compression reveals superior strength and ductility but an absence of damage in lamellar bone. Nat. Mater. 2014, 13, 740–747.
- Doblaré, M.; García, J.M.; Gómez, M.J. Modelling bone tissue fracture and healing: A review. Eng. Fract. Mech. 2004, 71, 1809–1840.
- Arnett, T. Osteocytes—Human Bone; Bone Research Society: Peterborough, UK, 2015.
- Arnett, T.; Manzano, J. Osteoclast Resorption; Bone Research Society: Peterborough, UK, 2015.
- Mackenzie, K. Osteocytes; Bone Research Society: Peterborough, UK, 2015.
- International Osteoporosis Foundation. Available online: https://www.osteoporosis.foundation/health-professionals/about-osteoporosis/bone-biology (accessed on 16 March 2022).
- Rosa, N.; Simoes, R.; Magalhães, F.D.; Marques, A.T. From mechanical stimulus to bone formation: A review. Med. Eng. Phys. 2015, 37, 719–728.
- Kohli, N.; Ho, S.; Brown, S.J.; Sawadkar, P.; Sharma, V.; Snow, M.; García-Gareta, E. Bone remodelling in vitro: Where are we headed?—A review on the current understanding of physiological bone remodelling and inflammation and the strategies for testing biomaterials in vitro. Bone 2018, 110, 38–46.
- Moharrer, Y.; Boerckel, J.D. Tunnels in the rock: Dynamics of osteocyte morphogenesis. Bone 2021, 153, 116104.
- Kola, S.K.; Begonia, M.T.; Tiede-Lewis, L.M.; Laughrey, L.E.; Dallas, S.L.; Johnson, M.L.; Ganesh, T. Osteocyte lacunar strain determination using multiscale finite element analysis. Bone Rep. 2020, 12, 100277.
- Ramani-Mohan, R.-K.; Schwedhelm, I.; Finne-Wistrand, A.; Krug, M.; Schwarz, T.; Jakob, F.; Walles, H.; Hansmann, J. Deformation strain is the main physical driver for skeletal precursors to undergo osteogenesis in earlier stages of osteogenic cell maturation. J. Tissue Eng Regen Med. 2018, 12, e1474–e1479.
- Kameo, Y.; Ozasa, M.; Adachi, T. Computational framework for analyzing flow-induced strain on osteocyte as modulated by microenvironment. J. Mech. Behav. Biomed. Mater. 2022, 126, 105027.
- Mak, A.; Zhang, J. Numerical simulation of streaming potentials due to deformation-induced hierarchical flows in cortical bone. J. Biomech. Eng. 2001, 123, 66–70.
- Scheiner, S.; Pivonka, P.; Hellmich, C. Poromicromechanics reveals that physiological bone strains induce osteocyte-stimulating lacunar pressure. Biomech. Model. Mechanobiol. 2016, 15, 9–28.
- Zhao, F.; Garrigle, M.J.M.; Vaughan, T.J.; McNamara, L.M. In silico study of bone tissue regeneration in an idealised porous hydrogel scaffold using a mechano-regulation algorithm. Biomech. Model. Mechanobiol. 2018, 17, 5–18.
- Yu, K.; Sellman, D.P.; Bahraini, A.; Hagan, M.L.; Elsherbini, A.; Vanpelt, K.T.; Marshall, P.L.; Hamrick, M.W.; McNeil, A.; McNeil, P.L.; et al. Mechanical Loading Disrupts Osteocyte Plasma Membranes Which Initiates Mechanosensation Events in Bone. J. Orthop. Res. 2018, 36, 653–662.
- Burra, S.; Nicolella, D.P.; Francis, W.L.; Freitas, C.J.; Mueschke, N.J.; Poole, K.; Jiang, J.X. Dendritic processes of osteocytes are mechanotransducers that induce the opening of hemichannels. Proc. Natl. Acad. Sci. USA 2010, 107, 13648–13653.
- Spasic, M.; Jacobs, C.R. Lengthening primary cilia enhances cellular mechanosensitivity. Eur. Cells Mater. 2017, 33, 158–168.
- Hemmatian, H.; Bakker, A.D.; Klein-Nulend, J.; van Lenthe, G.H. Alterations in osteocyte lacunar morphology affect local bone tissue strains. J. Mech. Behav. Biomed. Mater. 2021, 123, 104730.
- Hamed, E.; Jasiuk, I. Multiscale damage and strength of lamellar bone modeled by cohesive finite elements. J. Mech. Behav. Biomed. Mater. 2013, 28, 94–110.
- Kaya, S.; Basta-Pljakic, J.; Seref-Ferlengez, Z.; Majeska, R.J.; Cardoso, L.; Bromage, T.G.; Zhang, Q.; Flach, C.R.; Mendelsohn, R.; Yakar, S. Lactation-induced changes in the volume of osteocyte lacunar-canalicular space alter mechanical properties in cortical bone tissue. J. Bone Miner. Res. 2017, 32, 688–697.
- Sang, W.; Li, Y.; Guignon, J.; Liu, X.S.; Ural, A. Structural role of osteocyte lacunae on mechanical properties of bone matrix: A cohesive finite element study. J. Mech. Behav. Biomed. Mater. 2022, 125, 104943.
- Burr, D.B. Stress concentrations and bone microdamage: John Currey’s contributions to understanding the initiation and arrest of cracks in bone. Bone 2019, 127, 517–525.
- Josephson, T.O.; Moore, J.P.; Maghami, E.; Freeman, T.A.; Najafi, A.R. Computational study of the mechanical influence of lacunae and perilacunar zones in cortical bone microcracking. J. Mech. Behav. Biomed. Mater. 2021, 126, 105029.
- Uda, Y.; Azab, E.; Sun, N.; Shi, C.; Pajevic, P.D. Osteocyte Mechanobiology. Curr. Osteoporos. Rep. 2017, 15, 318–325.
- Dallas, S.L.; Prideaux, M.; Bonewald, L.F. The osteocyte: An endocrine cell… and more. Endocr. Rev. 2013, 34, 658–690.
- Lemaire, T.; Capiez-Lernout, E.; Kaiser, J.; Naili, S.; Rohan, E.; Sansalone, V. A multiscale theoretical investigation of electric measurements in living bone. Bull. Math. Biol. 2011, 73, 2649–2677.
- Bonewald, L.F. The amazing osteocyte. J. Bone Miner. Res. 2011, 26, 229–238.
- Dutta, S.K.; Datta, D. Composition of musculoskeletal structures. In Applied Orthopaedic Biomechanics, 1st ed.; Dutta, S.K., Datta, D., Eds.; BI Publications Pvt Ltd.: New Delhi, India, 2008; pp. 29–37.
- Mckibbin, B. The biology of fracture healing in long bones. J. Bone Jt. Surg. Br. 1978, 60-B, 150–162.
- Cartmell, S.; Rupani, A.; Balint, R. Osteoblasts and their applications in bone tissue engineering. Cell Health Cytoskelet. 2012, 49, 49–61.
- Aarden, E.M.; Nijweide, P.J.; Burger, E.H. Function of osteocytes in bone. J. Cell. Biochem. 1994, 55, 287–299.
- George, D.; Allena, R.; Remond, Y. Integrating molecular and cellular kinetics into a coupled continuum mechanobiological stimulus for bone reconstruction. Contin. Mech. Thermodyn. 2019, 31, 725–740.
- Martin, M.; Sansalone, V.; Cooper, D.M.; Forwood, M.R.; Pivonka, P. Mechanobiological osteocyte feedback drives mechanostat regulation of bone in a multiscale computational model. Biomech. Model. Mechanobiol. 2019, 18, 1475–1496.
- Zhang, X.; Wang, H.; Hao, Z. A numerical bone regeneration model incorporating angiogenesis, considering oxygen-induced secretion of vascular endothelial growth factor and vascular remodeling. J. Biomech. 2021, 127, 110656.
- Peyroteo, M.; Belinha, J.; Natal Jorge, R. Load adaptation through bone remodeling: A mechanobiological model coupled with the finite element method. Biomech. Model. Mechanobiol. 2021, 20, 1495–1507.
- Isaksson, H. Recent advances in mechanobiological modeling of bone regeneration. Mech. Res. Commun. 2012, 42, 22–31.
This entry is offline, you can click here to edit this entry!
