Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Stock portfolio management consists of defining how some investment resources should be allocated to a set of stocks. It is an important component in the functioning of modern societies throughout the world. However, it faces important theoretical and practical challenges. ANNs have high accuracy, fast prediction speed and clear superiority in predictions related to financial markets.
- stock portfolios
- artificial neural networks
- evolutionary algorithms
- computational intelligence
1. Introduction
1.1. Fundamental Analysis
One of the most used sources of information in the management of stock portfolios comes from the so-called fundamental analysis. The fundamental indicators provided by this analysis allow the practitioner to evaluate stocks from multiple perspectives. Such indicators are constructed from the financial statements that the companies (underlying the stocks) present publicly on a regular basis.
Fundamental indicators provide information that is often exploited in the literature to forecast future stock performance and to select the most competitive stocks. These indicators can be used both qualitatively and quantitatively. Regarding the latter, the financial information published by companies is synthesized in the form of ratios that shed light on the current state of the company, providing remarkable information on what can be expected from the financial health of the company and the possible future price of its stock. When this analysis is used in the literature, the fundamental indicators are usually aggregated in an overall assessment value that requires subjective preferences from the practitioner (cf. e.g., [13]); however, the aggregation procedure is not straightforward and represents an important challenge.
1.2. Artificial Neural Networks
Artificial neural networks are nowadays very popular among techniques from computational intelligence that have been used for many applications, such as classification, clustering, pattern recognition and prediction in diverse scientific and technological disciplines ([15,16]). Similarly to other computational intelligence techniques, applications of ANN are very diversified due to its capability to model systems and phenomena from the fields of sciences, engineering and social sciences.
Analogously to a nervous system, an ANN is built from neurons, which are the basic elements for processing signals. Neurons are interconnected to form a network, with additional connections (synaptic relations) for input and output signals. Weights are assigned to each of these and other connections. The computing of suitable values for these weights is performed by training algorithms. An ANN needs to be trained before it can be used by using actual data from the system or phenomenon to model. Neurons are configured to form layers, in which neurons have parallel connections for inputs and outputs. ANN complexity varies from a network with a single layer of a single neuron to networks with several layers, each having several neurons. Networks with only forward connections are known as feedforward networks. Networks with forward and backward connections are known as feedbackward networks ([15]). The term deep learning refers to ANN with complex multilayers ([17]). Roughly speaking, deep learning has more complex connections between layers and also more neurons than previous types of networks. Some neural networks that form deep learning networks are convolutional networks, recursive networks and recurrent networks.
2.3. Multi-Objective Optimization Problem
Without loss of generality, a multi-objective optimization problem (MOP) can be defined in terms of maximization (although minimization is also common) as follows:
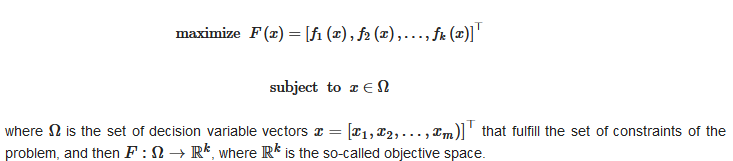
It is evident that the notation used here states that all functions fi (objectives) should be maximized; however, it is also possible that one requires some functions fi to be minimized instead. To keep standard notation, we assume that the latter can be simply achieved by multiplying the minimizing function by −1.
1.4. Evolutionary Multi-Objective Optimization
Multi-objective evolutionary algorithms (MOEAs) are high-level procedures designed to discover good enough solutions to MOPs (solutions that are close to the global optimum). They are especially useful with incomplete or imperfect information or a limited computing capacity ([19]).
MOEAs address MOPs using principles from biological evolution. They use a population of individuals, each representing a solution to the MOP. The individuals in the population reproduce among them, using so-called evolutionary operators (selection, crossover, mutation), to produce a new generation of individuals. Often, this new generation of individuals is composed of both parents and children that posses the best fitness; this fitness represents the impact on the objectives of the MOP. Since each individual encodes a solution to the MOP, MOEAs can approximate a set of trade-off alternatives simultaneously.
The performance of MOEAs has been assessed in different fields (e.g., [20,21]). They have been widely accepted as convenient tools for addressing the problem of stock portfolio management ([10,11,12]). The main goal of MOEAs is to find a set of solutions that approximate the true Pareto front in terms of convergence and diversity. Convergence refers to determining the solutions that belong to the PF, while diversity refers to determining the solutions that best represent all the PF. Thus, the intervention of the decision maker is not traditionally used in the process. Thus, rather little interest has been paid in the literature to choosing one of the efficient solutions as the final one in contrast to the interest paid in approximating the whole Pareto front.
Usually, two types of MOEAs are highlighted in the literature: differential evolution and genetic algorithms. Differential evolution (DE) has been found to be very simple and effective ([22]), particularly when addressing non-linear single-objective optimization problems ([23,24]). On the other hand, in a genetic algorithm (GA), solutions to a problem are sought in the form of strings of characters (the best representations are usually those that reflect something about the problem that is being addressed), virtually always applying recombination operators such as crossing, selection and mutation operators. GAs compose one of the most popular meta-heuristics applied to the Portfolio Optimization Problem ([12]).
2. Computational Intelligence in Stock Portfolio Management
2.1. Portfolio Management: Price Forecasting, Stock Selection and Portfolio Optimization
In recent years, there have been plenty of contributions on price forecasting based on either statistical or computational intelligence methods (see [10,27]). The stock market is characterized by extreme fluctuations, non-linearity, and shifts in internal and external environmental variables. Artificial intelligence techniques can detect such non-linearity, resulting in much-improved forecast results [28].
Among the computational intelligence methods used for price forecasting are deep learning (e.g., [29,30,31,32]) and machine learning (e.g., [33,34,35]). In [10], a hybrid stock selection model with a stock prediction stage based on an artificial neural network (ANN) trained with the extreme learning machine (ELM) training algorithm ([6,36]) was proposed. The ELM algorithm has been tested for financial market prediction in other works (see [7,8,9]).
There are important works on methods for stock selection, which have several different fundamental theories, from operations research methods (e.g., [37,38]) to approaches originating in modern portfolio theory (Mean-variance model) (e.g., [38,39]) and soft computing methods (e.g., [40,41]), including hybrid approaches (e.g., [10,42,43]).
The fundamental theory for portfolio optimization is Markowitz’s mean-variance model ([44]). Its formulation marked the beginning of Modern portfolio theory ([45]). However, Markowitz’s original model is considered too basic since it neglects real-world issues related to investors, trading limitations, portfolio size and others ([43]). For evaluating a portfolio’s performance, the model is based on measuring the expected return and the risk; the latter is represented by the variance in the portfolio’s historical returns. Since the variance takes into account both negative and positive deviations, other risk measures have been proposed, such as the Conditional Value at Risk (CVaR) ([46,47]). As a result, numerous works have improved the model, creating more risk measures and proposing restrictions that bring them closer to practical aspects of stock market trading ([27]). Consequently, many optimization methods based on exact algorithms (e.g., [48,49,50,51,52,53,54,55]) and heuristic and hybrid optimization (e.g., [29,56,57,58,59,60,61,62,63,64,65]) have been proposed to solve the emerging portfolio optimization models ([27,40,45]).
2.2. Exploiting Uptrends and Downtrends in Strategies for Stock Investment
Regarding alternative strategies to the known buy-and-hold approach for stock investment, in ([69]), the authors propose two new trading strategies to outperform the buy-and-hold approach, which is based on the efficient market hypothesis. The proposed strategies are based on a generalized time-dependent strategy proposed in ([70]) but propose different timing for changing the buying/selling position. According to ([71]), the decision to adopt a long or short position in an asset requires a view of its immediate future price movements. A typical short seller would have to assess the potential future behavior of the asset price by means of evaluating several factors, such as past returns and market effects as well as technical indicators, such as market ratios ([71]). There are a few works published in the literature to address the problem of trading strategies for the short position. An interesting work that considers not only the short position but both the short and long positions is ([72]), in which a simultaneous long-short trading strategy (SLS) is proposed. Such a strategy is based partially on the property that a positive gain with zero initial investment is expected, which holds for all discrete and continuous price processes with independent multiplicative growth and a constant trend. Other works based on SLS are ([73,74,75]).
Building stock portfolios with high returns and low risk is a common challenge for researchers in the financial area. Usually, the most common practice is to select the more promising stocks according to several factors, such as financial information, news of the market and technical analysis. Several approaches that use computational intelligence algorithms have been proposed in the literature to deal with the overwhelming complexity of building a stock portfolio. Usually, these approaches consider up to three activities to build a portfolio: return forecasting, stock selection and portfolio optimization. These activities decide which stocks should be supported, as well as the proportions of the investment to be allocated to them, by comparing the historical and forecasted performance of potential stock investments.
Given the approaches mentioned above for addressing the three activities or stages: return forecasting, stock selection and portfolio optimization, a comprehensive approach for portfolio bulding and optimization can be carried out by applying a combination of computational intelligence techniques in each stage. A particular effective combination proven in the literature comprises: stock price forecasting by an artificial neural network (ANN) trained by the extreme learning machine (ELM) algorithm. Stock selection is modeled as an optimization problem that seeks to determine the most plausible stocks; thus, a differential evolution is exploited on the basis of the forecasted price and a set of factors of the so-called fundamental analysis. Finally, portfolio optimization is conducted through a genetic algorithm that uses confidence intervals of the portfolio returns to determine the best stock portfolio. It is worth to mention that forecasting the price of a given stock allows the comprehensive approach to focus on uptrends or downtrends (i.e., going long or short, respectively) for that stock.
This entry is adapted from the peer-reviewed paper 10.3390/app12084067
This entry is offline, you can click here to edit this entry!
