One of the key elements for robot applications is autonomously navigating and planning a trajectory according to surrounding space obstacles. In the context of navigation systems, self-localization and mapping are pivotal components, and a wide range of sensors—from exteroceptive ones, such as the Global Positioning System (GPS), to proprioceptive ones, such as inertial measurement units (IMUs), as well as light detection and ranging (LiDAR) 3D scanners, and cameras—have been employed in the search for a solution to this task. As humans experience the rich amount of information coming from vision daily, exploring solutions that rely on a pure imaging system is particularly intriguing. Besides, relying only on visual clues is desirable as these are easy to interpret, and cameras are the most common sensor mounted on robots of every kind.

Visual simultaneous localization and mapping (V-SLAM) methods aim to optimize the tasks of motion estimation, that is, the 6 degrees of freedom (6DoF) transform that relates one camera frame to the subsequent one in 3D space, and 3D scene geometry (i.e., the depth and structure of the environment), in parallel. Notably, due to the interdependent nature of the two tasks, an improvement on the solution for one influences the other. On the one hand, the mapping objective is to maintain global consistency of the locations of the landmarks, that is, selected points of the 3D world that SLAM tracks. In turn, revisiting a previously mapped place may trigger a loop-closure [1], which activates a global optimization step for reducing the pose residual and smoothing all the past trajectory errors [2]. On the other hand, visual odometry (VO) [3] intends to carry out a progressive estimation of the ego-motion without the aspiration of obtaining a globally optimal path. As such, we can define VO as a sub-component of V-SLAM without the global map optimization routine required to minimize drift [4]. However, even VO methods construct small local maps composed by the tracked 2D features, to which a depth measurement is associated either through triangulation [5] or probabilistic belief propagation [6,7]. In turn, these 3D points are needed to estimate the motion between future frames.

Unsupervised methods have gained popularity for camera motion estimation and 3D geometry understanding in recent years [8]. Especially regarding monocular VO, approaches such as TwoStreamNet [9] have shown equally good or even superior performances compared to traditional methods, such as VISO2 [10] or ORB-SLAM [11]. The unsupervised training protocol [12] bears some similarities with the so-called direct methods [13]. Both approaches synthesize a time-adjacent frame by projecting pixel intensities using the current depth and pose estimations and minimizing a photometric loss function. However, the learned strategy differs from the traditional one because the network incrementally incorporates the knowledge of the 3D structure and the possible range of motions into its weights, giving better hypotheses during later training iterations. Moreover, through learning, we can overcome the typical issues of traditional monocular visual odometry. For example, the support of a large amount of example data during training can help solve degenerate motions (e.g., pure rotational motion), scale ambiguity and scale drift, initialization and model selection, low or homogeneously textured areas, and perceptual aliasing [4]. However, being aware of the solid theory behind the traditional methods [14] and their more general applicability, we leverage geometrical image alignment to improve the pose estimation.

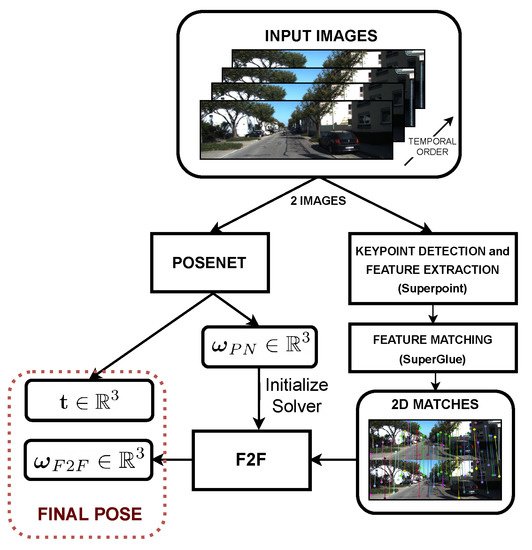
Therefore, in this work, we present RAUM-VO. Our approach, shown in Figure 1, combines unsupervised pose networks with two-view geometrical motion estimation based on a model-free epipolar constraint to correct the rotations. Unlike recent works [15,16] that train optical flow and use complex or computationally demanding strategies for selecting the best motion model, our approach is more general and efficient. First, we extract 2D keypoints using Superpoint [17] from each input frame and match the detected features from pairs of consecutive frames with Superglue [18]. Subsequently, we estimate the frame-to-frame motion using the solver proposed by Kneip et al. [19], which we name F2F, and use the rotation to guide the training with an additional self-supervised loss. Finally, RAUM-VO efficiently adjusts the rotation predictions with F2F during online inference, while retaining the scaled translation vectors from the pose network.

The difference between SLAM and VO is the absence of a mapping module that performs relocalization and global optimization of the past poses. Aside from this aspect, we can consider contributions in monocular SLAM works seamlessly with those in the VO literature. A primary type of approach to SLAM is filter-based, either using extended Kalman filters (EKFs) (as in MonoSLAM [20]) or particle filters (as in FastSLAM [21]), and keyframe-based [5], referred in robotics to as smoothing [22]. This name entails the main difference between keyframe-based and filtering. While the first optimizes the poses and the landmarks associated with keyframes (a sparse subset of the complete history of frames) using batch non-linear least squares or bundle adjustment (BA) [23], the latter marginalizes past poses’ states to estimate the last at the cost of accumulating linearization errors [24]. In favor of bundle adjustment, Strasdat et al. [25] show that the accuracy of the pose increases when the SLAM system tracks more features and that the computational cost for filtering is cubic in the number of features’ observations, compared to linear for BA. Thus, using BA with an accurate selection of keyframes allows more efficient and robust implementations of SLAM. Unsupervised methods are more similar to the keyframe-based SLAM. The motion is not the result of a probabilistic model propagation and a single-step update but of an iterative optimization to align a batch of image measurements.

Motion estimation approaches fall into either direct or indirect categories based on the information or measurements included in the optimized error function. The direct method [13,26] includes intensity values in a non-linear energy function representing the photometric difference between pixels’ or patches’ correspondences. These are found by projecting points from one frame to another using the current motion and depth estimation, which is optimized either through the Gauss–Newton or Levenberg–Marquardt method. Instead, indirect methods [5,11] leverage epipolar geometry theory [14] to estimate motion from at least five matched 2D point correspondences, in the case of calibrated cameras [27], or eight, in the case of uncalibrated cameras [28]. After initializing a local map from triangulated points, perspective-n-point (PnP) [29] can be used with a random sample consensus (RANSAC) robust iterative fitting scheme [30] to obtain a more precise relative pose estimation. Subsequently, local BA refines the motion and the geometrical 3D structure by optimizing the reprojection error of the tracked features.

The pioneering work of Garg et al. [31] represents a fundamental advancement, because they approached the problem of depth prediction from a single frame in an unsupervised manner for the first time. Their procedure consists of synthesizing a camera’s depths in a rectified stereo pair by warping the other using the calibrated baseline and focal lengths. Godard et al. [32] use the stereo pair to enforce a consistency term between left and right synthesized disparities, while adopting the structural similarity (SSIM) metric [33] as a more informative visual similarity function than the L1

loss. SfM-Learner [12] relies entirely on monocular video sequences and proposes the use of a bilinear differentiable sampler from ST-Nets [34] to generate the synthesized views.

Because the absolute metric scale is not directly observable from a single camera (without any prior knowledge about object dimensions), stereo image pairs are also helpful to recover a correct metric scale during training while maintaining the fundamental nature of a monocular method [35,36,37]. Mahjourian et al. [38] impose the scale consistency between adjacent frames as a requirement for the depth estimates by aligning the 3D point clouds using iterative closest point (ICP) and approximating the gradients of the predicted 6DoF transform. Instead, Bian et al. [39], arguing that the previous approach ignores second-order effects, show that it is possible to train a globally consistent scale with a simple constraint over consecutive depth maps, allowing one to reduce drift over long video sequences. In [40], a structure-from-motion (SfM) model is created before training and used to infer a global scale, using the image space distance between projected coordinates and optical flow displacements. More recently, several approaches [15,16,41] have leveraged learned optical flow dense pixel correspondences to recover up-to-scale two-view motion based on epipolar geometry. Therefore, they resolve the scale factor by aligning a sparse set of points with the estimated depths.

One of the main assumptions of the original unsupervised training formulation is that the world is static. Hence, many works investigate informing the learning process about moving objects through optical flow [42,43,44,45,46,47,48,49,50,51,52,53]. The optical flow, which represents dense maps of the pixel coordinates displacement, can be separated into two components. The first, the rigid flow, is caused by the camera’s motion. The second, the residual flow, is caused by dynamic objects that move freely in relation to the camera frame. Therefore, these methods train specific networks to explain the pixel shifts inconsistent with the two-view rigid motion. However, these methods focus principally on the depth and optical flow maps quality and give few details about the impact of detecting moving objects on the predicted two-view motion. Notably, they use a single metric to benchmark the relative pose that is barely informative about the global performance and cannot distinguish the improvements clearly.

A recent trend is to translate traditional and successful approaches such as SVO [54], LSD-SLAM [26], ORB-SLAM [11], and DSO [13] into their learned variants, or to take them as inspiration for creating hybrid approaches, where the neural networks usually serve as an initialization point for filtering or pose graph optimization (PGO) [55,56,57,58,59,60,61,62]. However, RAUM-VO focuses on improving the predicted two-view motion of the pose network without introducing excessive computation overhead as required by a PGO backend.

Instead of training expensive optical flow, RAUM-VO leverages a pre-trained Superpoint [17] network for keypoint detection and feature description and Superglue [18] for finding valid correspondences. Unlike optical flow, the learned features do not depend on the training dataset and generalize to a broader set of scenarios. In addition, using Superglue, we avoid heuristics for selecting good correspondences among the dense optical flow maps, which we claim could be a more robust strategy. However, we do not use any information about moving objects to discard keypoints lying inside these dynamic areas. Finally, differently from other hybrid approaches [15,16], we do not entirely discard the pose network output, but we look for a solution that improves its predictions efficiently and sensibly. Thus, the adoption of the model-free epipolar constraint of Kneip and Lynen [19] allows us to find the best rotation that explains the whole set of input matches without resorting to various motion models and RANSAC schemes. To the best of our knowledge, we are the first to test such an approach combined with unsupervised monocular visual odometry.