Abstract: Consider an evolutionary process. In genetic inheritance and in human cultural systems each new offspring is assigned to be produced by a specific pair of the previous population. This form of mathematical arrangement is called a surjection. We have thus briefly described the mechanics of genetics – physical mechanics describes the possible forms of loci, and normal genetic statistics describe the results as viability of offspring in actual use. But we have also described much of the mechanics of mathematical anthropology. Understanding that what we know as inheritance is the result of finding surjections and their consequences, is useful in understanding, and predicting, biological, as well as cultural evolution. he review shows us that in describing evolution, two sorts of statistics are required: those that follow specific inheritance of actual surviving individuals from specific mating, and those which follow population averages on a large class of individuals. The author believes the most important part of this discussion are the comments and citations to the work of Lila Gatlin in Parts 8 and 9 of the text. (This version of text submitted on March 3, 2020.)
- surjection
- biological evolution
- mathematical anthropology
- predicting biological evolution
- predicting cultural evolution
- mathematical groups
Inheritance is a Surjection: Description and Consequences (Second Edition)
Paul Ballonoff
Correspondence: Paul@Ballonoff.net; Tel.: +1-703-780-1761
(Write to Paul@Ballonoff.net for a PDF version which may have better notation of this text)
1. Description of Study
The basic mathematical description from finding inheritance is a surjection is summarized in Part 2 below. By concentrating on the notion of “surjection” we are forced to observe, from mathematical theorems in Part 2, that two things that must occur simultaneously: the offspring population must all be unique individuals; and the parental pairs must be using identical or isomorphic means of creating the offspring. Our normal discussion of phylogenetics imply that the parents are using the “same” genetic means (thus that their treatments are identical or isomorphic); but the results of Part 2 shows that we must prove that.
Thus in part 3 provides a detailed description that all offspring are unique, both for humans and other offspring. In Part 3 we also present the Mendelian arrays of results of breeding relationships, and their traditional statistics. Nothing in seeing that inheritance is a surjection changes what the methods of Part 3 detect. We must also recognize that all parental “couples” act under identical or isomorphic methods allowed, and all are acting under identical (isomorphic) methods allowed by specific mathematical groups. The proof is in the articles of Part 4.
For population genetics, to count the results of using possible different alleles at each locus, we must count the total number of surviving offspring from each parental pair. In physical mechanics the creation and the intervals of reproduction are potentially observable within normal human perception; usually they occur in very short periods. Thus in population genetics, counting of the number of offspring from each pair of “parents” is the actual number of offspring surviving from each pair that reproduce.
In culture theory, existing literature shows that mathematical groups occur as a means of describing the mechanism of each culture’s rules of kinship and marriage. But human cultural systems may require decades of time for one generation to be replaced by another. Each human culture has its own culturally determined means of assigning offspring to parental pairs. Depending on the culturally specific rules, each parental pair’s offspring may include their own genetic offspring, but also may follow culturally designated devices such as adoption. Thus for human cultures, the assigned offspring may include individuals who may have no genetic relation to the “parents”.
However when we recognize that the human means of describing kinship and marriage is also a surjection, we see from Part 2 that we can apply the Stirling Number of the Second Kind (SNSK). Cultural rules allow that offspring are not necessarily biologically related to their assigned parents. Use of the SNSK statistics however permits us to find the expected population statistics without assuming they are biologically related. Using SNSK thus allows us to interpret the past, and make forecasts of the future, in association with the culturally specific rules of marriage, which traditional demographic analysis does not treat. This result is discussed in Parts 5 and 6 below. The results in Part 6 also shows us that recognition of surjection allows us to treat issues that have not been treated by other methods; we thus give specific examples, and how the analysis gives new and unique results. Our discussion in Parts 5 and 6 is a bit longer than others here, since the topic has not been broadly discussed, though the underlying principles, including examples, have been in published articles since 1982.
In Part 7 we discuss more recent issues, based on thoughts of predicting future biological and human evolution, as has been proposed in recent literature. The fact that future evolution is governed by a surjection, also means both the present condition, and any future evolution, must be based on molecules determined by a limited set of mathematical groups. In other parts of physics, when results are based on mathematical groups, the future may also be formed into classes determined by those groups. That result also follows for population genetics. But to fully recognize that requires we add to the list of Part 3, measures based on entropy; Part 8 is a brief summary. Part 9 is a summary of results. In both Parts 8 and 9 we note the brilliant work of L. Gatlin in describing how biological evolution is a necessary part of physics.
2. Foundation Discussion
In genetics, the biological descendants are the actual biological descendants of the identified parental pair. In human systems, the descendants may be the actual biological descendants of the parental pair, but may also reflect other cultural assignments, such as by (non-inherited) devices such as adoption. In both cases, we have a mapping from each offspring to a particular set of parents. The well know mathematical name for this relation is surjection. Theorems on how inferences are made for surjections include [1 page 178], [2], [3] and [4]. Look especially at [1, page 178] and [4] for the author’s “Twelvefold Way” pages 69-79.
The theorems cited in [1, 2, 3, 4] show that finding that a relation is a surjection also means that the newly created offspring individuals are each “unique”, and the entities to which offspring are assigned by their parental organisms are identical or isomorphic in how the parents act. Neither of those notions was in our concepts of the subjects here. We do not assume that surjection causes these results, but if we find out that they are not true, it means our assessment that the processes form a surjection is wrong. This we must first demonstrate if “uniqueness” and “identical or isomorphic forms of reproduction” are correct descriptions, to believe we have correctly described the process as a surjection.
3. Uniqueness of Offspring
When we say that the offspring of an evolutionary process are unique, we mean that there is at least one, but may be many differences between each of those offspring. Radzevilavicius and Blackstone’s [5] very detailed review of the evolution of individuality of offspring populations shows that all individuals, of all species, created by evolution are also in some form unique; the reader should see that article for its many details. Thus [5, page 1630] concludes “since [our review] … only relies on universal principles of life’s evolution, this framework can potentially be applied to all life, no matter what its chemistry, and wherever it is found”.
The mathematics that describes how biological evolution works began in the late 19th Century, representing the frequency or relative frequencies of alternative alleles at specific loci. If we define a single species, there are common sets of DNA/RNA which define that single species. But there may also be recombination of the alleles that can act at each loci [6]; [5] made a similar observation. These variants may create features in specific offspring that are not determined by the common genes in all of that species. Thus despite isomorphism in the defining characteristics of a species (isomorphism in following the DNA/RNA genetic codes that define that specific species), the uniqueness of individuals includes some differences, which may be differences in specific DNA/RNA alleles, differences in recombination of DNA/RNA in their individual coding sequence, and from other genetically coded individual differences.
The first such description was by Mendel [7], followed in the early 20th century by Bernstein [8, 9]; Fischer [10]; Haldane [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]; Wright [21]; Nei [22]; Crow and Kimura [23] and others. There are useful overall comparisons of those methods including [24, 25, 26, 27, 28, 29, 30] and others. Though each of those authors uses somewhat different mathematical representations to determine the allele frequencies in specific cases, all show that devices such as those of Mendel allow many different forms of inheritance. There are many possible locus sites in each organism, and in nearly all organisms there may be diverse alleles at some or many sites; so each individual may have hundreds, or thousands, or indeed many multiple thousands, of diverse sites per organism. Thus individual uniqueness is not difficult to understand. While isomorphism of certain alleles at certain sites may define a specific species, the distinct frequencies in some or many other loci sites of individuals are one of the many reasons why unique individual types of each species exist.
4. Identical Means of Reproduction
We must also show that each of the genetic parental pairs must use identical or isomorphic means of reproduction. This has been shown since the basic mechanics for construction of DNA and RNA molecules are also structured by group-theoretical results of physical mechanics. For the mechanisms of DNA, see for example the articles of Petoukhov [31, 32, 33, 34, 35], Petoukhov and Castro-Chaves [36], Petoukhov and Hu [37], Petoukhov, Petoukhova and Svirin [38], Hainen [39]’ Rakocevic [40] and others, who have demonstrated that the DNA devices used for genetic reproduction are described by mathematical groups by physical mechanics. For RNA, see similar work, also using similar groups of 64 codons, that have been described by Khrennikov and Kozyrev, Rakocevic, and by A. Dragovich and B. Dragovich [41, 42, 43, 44, 45, 46]. A simple basic description of genetic mechanisms represented is found for example in [38], using descriptions of the 64 codons of DNA with the arrangements of all members in accordance with the binary-oppositional signs of the bases A, C, G and T.
While in each act creating new offspring, the specific objects of the genes (DNA and/or RNA) are distinct objects, the fact that all must satisfy specific group-theoretical forms, means that the isomorphisms of those group theoretical forms (required by how alleles may form under the allowed physical mechanics) means that all organisms are formed using the specific sets of mathematical groups, thus acting under isomorphic rules of combination. They thus are following isomorphic sets of rules of how the offspring may be created, which being part of a surjections implies they must be doing.
5. Kinship
Ballonoff [47, 48] recently reviewed the literature of mathematical anthropological description, in relation to the ability of a system to survive. The earliest paper for mathematical description of kinship is from 1882: [49] modeled strings of symbols to represent semantic concepts, such as “MBD” (mothers brothers daughter) for an instance of part of the English term “first cousin”. But in 1945 ethnographer Ruheman [50] created the first description of kinship which identified objects that are clearly mathematical groups. 
Ruheman denoted each cultural system by placing names of kinship relations onto finite sets of offspring in the culture’s language, used diagrams to show how a terminology relates those sets of labels onto representative minimal set of parents, and assumed each system had distinct generations. In this example, she used labels A and B for moiety names. Descents of a male of A are also called A; descendants of a male of B are also called B; the top layer is one generation of two sets of moieties, with two marriages, which reproduces in one generation another set of A and B moieties. Her illustrations use the symbol “=“ for a "marriage" between two individuals; two sets of parallel but opposite arrows between individuals as “brothers and/or sisters”; and placed objects into columns labelled m and f for males and females. The arrows or = signs on each end of each line connect to the persons on the other end of each line.
This system thus has at least two sets of marriages in each generation; each A always marries a B. In each generation, each generation minimal structure has two marriages. That minimal group has an order; let the minimal group size order = s. Thus the structural number of a rule is equal to the size of the minimal group representing that rule. Thus for the rule shown in Figure 1, the structural number of that rule is s = 2.
To create a diagram like Figure 1, [50, page 543] said:
“… The system must be self-contained and consistent; must provide a sufficient number of descent lines (a) to enable every member to select a spouse from his own generation; (b) to allow space for every distinct relationship term; and no [kinship] term may appear more than twice … in any one generation. … The system must be able to reproduce itself after a number of generations. …”.
And thus [50, page 576] said that by using mathematical representations,
“… It is independent of any special principles, which might at best be controversial, and proceeds simply from a systematic arrangement of the recorded facts; … It enables the dominating features of even a very complex system of kinship terms to be brought into full view in a single picture; … It makes possible the comparison and classification of widely divergent kinship systems, and provides a useful check on the completeness of our information.”
Ruheman’s methods do not therefore discuss many of the issues often treated in non-mathematical analysis of cultural systems. Avoiding non-mathematical descriptions is one of her purposes.
The mathematical groups for each minimal set of kinship terms described by Ruheman (or Weil as cited in the end of this paragraph) is also now called the minimal structure [47] of that system of kinship description. It is also described [47, 48] as the history of that system since it describes how possible parental pairs of that culture may be created. The minimal structure is not a literal description of how all marriages work, it is merely the minimal size for the rule which describes it, though in some cases some empirical relations can also look like the Ruheman minimal descriptions in some ethnographies. The minimal kinship diagrams also look like the illustrations of ( a minimal) regular genetic systems of inbreeding shown by Wright [21]. Just as in cultural analysis, the ability to show a minimal representation does not mean that all implementations of an experiment to do inbreeding must look exactly like the minimal form. But representations are very useful. Petoukhov [51] thus also demonstrated that there are similar mathematics behind analyzing literary texts (thus including analyzing kinship in human languages) and long genetic texts. When analyzing the specific minimal mathematical groups for describing the human Dravidian kinship categories, Vaz [52] showed that mathematical representation of Dravidian were isomorphic to the mathematical groups that describe DNA/RNA. While Ruheman created the notion, the most referenced “first” published text using group mathematics for kinship is often that created by the mathematician Andre Weil [53], in an appendix to Claude Levi-Strauss’ 1947 nook, The elementary structures of kinship [54]. Weil’s initiative was then expanded by [55, 56, 57, 58] and others, including others noted below; for example use of Cayley groups was described in [59].
One apparently difficulty of doing logical and algebraic manipulations on kinship data is that mathematical groups require an associative operation that creates the mathematical group on elements of the language. But human languages are not associative. In English, compare “Tom shows” to “shows Tom”. Thus the first work showing that kinship rules are actually non-associative algebras, but still consistent with the mathematics cited here, was [60]. A non-associative algebra can have an associative sub-set (the kinship rules for example), which are allowed by [60] and required by [48]. [61] is the first paper which derives mathematical kinship groups entirely from purely mathematical assumptions. [62, 63] elaborated many group-theoretical examples of kinship systems. [64] reviewed Weil’s original work and its subsequent history. [65] extended Weil’s work by using semigroups and homomorphisms among semigroups, as well as groups. Other extensions include [66, 67, 68, 69, 70, 71].
In 2018 a series of eight articles greatly expanded the depth of analysis of kinship [72, 73, 74, 75, 76, 77, 78, 79]; readers should see those articles also for their added citations. Many of those papers also seeking to relate kinship groupings directly to other concepts of cultural order; [60] sought the same results. Thus Read [73, page 54] cited the necessity of mathematical groups in kinship descriptions:
“… Because the core structure for classificatory terminologies has inverses and not just reciprocity between ascending and descending kin terms, the core structure is a group; that is, an algebra with an (associative) binary product, an identity element, and an inverse for each element in the algebra.”
Read is thus describing the empirical facts that make Ruheman’s concepts necessary.
Finally, while this author does not advocate that all analysis use mathematical representations for all problems of human kinship (nor that they solve all relationship issues), Harris [61] has considered this. His conclusion is:
“This paper represents relations among individuals as mathematical relations … and defines a relation ‘alter’. … ‘alter’ is shown to be an equivalence relation, and the equivalence classes generated and the ‘categories of equivalent people’ mentioned above … can be pairs to form a ‘clan’… or to form a marriage type … Moreover, our assumptions restricting allowable relations are used to prove as theorems the assumptions of previous authors restricting allowable permutation groups.”
Thus, we believe that using the descriptions of human kinship terms using their minimal mathematical groups, is a valid basis for the analysis used here.
6. Culture and Population Measurements
Summarizing Part 5, knowing the order of a culture’s minimal group, and using the fact that inheritance is a surjection, allows us to predict present and future populations statistics for that culture. In Part 6 we discuss how to do that, using the percentage of the population at time t using a history a with structural number s, and the fact that for each s there is are specific values ns (average family size) and ps (percentage of reproducing married females). We can then forecast demographic measures of average family size of the population n(t) and average percentage of females as producers of the offspring group p(t) found as weighted average of the percentage of society with structural number s, added over the entire society at each t. We define this in more depth below, with examples.
Each culture assigns each offspring individual in t to a specified parental pair of the previous generation t-1. For the “reproduction” assigned to each parental pair, there may be actual mating between them, but there may also be other means of the culture to assign offspring to that parental pair. These include “cheating” (sometimes known but often not known to other members of the population), assignment of other non-genetic offspring by adoption, and other means of assigning offspring to each parental pair. [1, 2, 3, 4] show that surjection means that the possible average numbers of offspring to parental pairs can be done by the Stirling Number of the Second Kind (SNSK), which do not require biological assignment as the means of assigning offspring to parents. We implement that computation using Equations 1 through 4 below. While ethnographic studies are usually done from a few months to several years, observations over several decades are needed since the results are in “generations”; each generation typically takes from 20 to 30 years. Our empirical examples summarized below give results closely matching what the results from analysis of the potential structural numbers in Equations 1 through 4 shows us.
Many things affect population size; this article is not an attempt to identify nor describe most of those. The demographic idea of the Leslie matrix [80, 81] produces a growth rate and stable age distribution as eigenvalues and eigenvectors of a matrix of age-structured mortality and fertility or fecundity rates. This reflects the approach of Lotka [82] that the “normal” demographic discussion of the growth of populations is analogous to “capital” growth in economics. Neither the Leslie matrix nor the Lotka models treats the cultural system, and thus do not predict consequences on population change due to changes in the cultural system (that is, due to changes in the history). We shall remove that limitation related to Lotka in our discussion in our Part 8.
Now please look at our Part 10 Definitions to define the mathematical objects shown in the illustration just below. In the illustration below, the formulas that determine the objects described by the math in the object D are results from demographic processes. The surjection requirement of using SNSK as cited in Part 2 allows us to predict how the demographics -- measures of of n(t) and p(t) -- of a population may change, as the histories change. To explore this [83] defined: 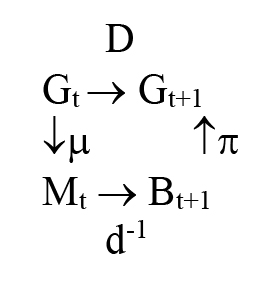 Assignments of offspring and parental pairs are, in each case, what are required by the specific rules of genetics or cultural assignment applied.
Assignments of offspring and parental pairs are, in each case, what are required by the specific rules of genetics or cultural assignment applied.
We now show how to use the surjections of cultural theory to derive cultural population estimates suing Equations 1 to 4 defined below. We then summarize applications from previously published articles. Let s be the structural number of history a. Let ns = average family size of a system with structural number s, and define the proportion of (socially ascribed) reproducing females as ps. Let ps = 2/ns. The specific values of ps, and ns by the rules structural number s are listed in [3 appendix 2], and further cited in [47, 84, 85]. Note that ns is always ≥ 2, so n*p = 2, or
- ½ (ns* ps) = 1.
Since we can set er(t) = 1, then we can also derive a general equity growth equation for any system with structural number s:
- er(t) = ½ n*p.
We call the exponential form r(t) equity growth to distinguish it from the capital growth idea per Lotka. But as Lotka also used a notation “r(t)” for capital growth so we here instead call Lotka’s capital growth rate here as R(t) to distinguish it from our own r(t); in Equation 4 below we derive an estimate of Lotka’s capital growth R(t) from our the equity growth r(t).
We use the values ns, ps given a history of structural number s, as stated in [3 appendix 2]. If we have just one structural number, since nsps = 2, then Equation 2 results in r(t) = 0. When r(t) = 0, it shows that the values of ns and ps allow a culture with history a and structural number s to have neither growth nor decline. As structural number s increases (above s = 3), then from [3] at its appendix 2, and [47, 84, 85] for a cultural system with only one cultural rule (one history) then the values of ns increase and ps decrease, to maintain cultural stability with zero change r(t) = 0. Another way to state this same result is that if the cultural systems gets “more complex” (as the structural number s increases) then the average family size ns per household also increases -- that is similar to the notion that as general systems become more complex, their per couple equity growth size must increase to maintain the same level of reliability of the entire system; that ism when r(t) = 0.
Now let the population at time t use some set of histories a, …, b. Then the proportion of each generation population Gt using history a is vat , the proportion of Gt using history b is vbt, etc. We require that 0 ≤ vat,, …, vbt ≤ 1 and SUMvat = 1 over all histories allowed in time period t. Then the average family size, averaged over all couples in time t is n(t) = SUMvatns, and the average proportion of females allowed to fertilize is p(t) = SUMvatps over all histories allowed at time t. We thus get an equation that allows prediction at time t of the time-dependent average population measures for n(t), p(t) and r(t) as the percentages of histories a, …, b change:
- er(t) = ½ n(t)*p(t).
Thus in Equation (3) then r(t) = 0 whenever all rules have the same structural number (or all have only s = 2 or 3). But r(t) ≠ 0 whenever there is a change in cultural dynamics by allowing rules with more than one structural number, and at least one of structural number > 3; all such changes cause population growth (or decline). This is well known by anthropologists: as cultures change, population statistics can also change. It is however predicted by the mathematics of cultural theory, using implications under the SNSK, as revealed by the mathematics of surjection, to find this.
To relate r(t) to the demographic notion R(t) we applied the mathematics originally developed for analysis of financial leverage (see [86] Chapters 3 and 4, [84] especially its Equation 17, and [85]), which there derives and shows:
- R(t) = 2 p(t)r(t) / [p(t)2 + 2r(t)].
Equation 4 is also called the amplification equation since it increases the usually much smaller equity growth value of r(t) into a larger capital growth value R(t). It can also be called amplification of local survivability, or, by analogy to borrowing of capital in the world of finance, “leverage”. The reader can look at [47, 48, 84, 85, 87, 88] for more details and citations of numerous examples.
One of the useful results of finding that cultural rules of kinship and marriage are surjections, is that the theorems of Part 2 allow is to apply the statistics of the statistic SNSK. Most of the “standard statistics” taught in academic statistics courses are in fact adaptations of the distributions of volumes of identical gas particles, distributed into specific (and distinct) parts of real space. But surjection means we have unique offspring, being assigned to parents who use identical or isomorphic means of process. The assumptions of the surjection are thus the opposite of what is required by standard academic statistics. But the statistics of SNSK are exactly what is required: unique objects (as unique individuals in the offspring population), together with similar means of treatment by the parents (as provided by isomorphic means of mechanisms of inheritance allowed by mathematical group theory in the specific molecules allows by references of Part 4).
Thus since we have a surjection, the use SNSK allows us to make important predictions of what may exist in real ethnographies, which can also be verified. For example, [84] used the changes in the structural numbers as listed in the table at [3, appendix 2] to predict the changes in Western European population statistics from about AD 1000 to about AD 1950. Early in that period we had relatively higher structural numbers in Western Europe, since for example, the Catholic Church had higher degrees of prohibition of relatives as marriage partners, thus higher structural numbers, thus higher values of ns. By the middle of the twentieth century, there became a much higher percentages of the population following more “Protestant” rules, which in general had lower values of s, thus lower values of ns. [84] followed these changes, and also discussed what may have happened when the black-plague took place – it may be that when that happened, there were also lower densities of marriageable people in local populations, but the rules needed a high ns. The ability of the population to create that ns was (locally) not physically present. The Protestant changes took place in that period, and also lead to a new marriage rule which lowered the ns for the newer Protestant populations. We do not claim here that our statistics tell us exactly what changes, or that what we call “Protestant” were the only choices. But [48] discusses that the possible changes among the available sets of histories at time t, might also limit what choices are available, and thus may limit what alternate forms of histories might be possible. The reader might also look at examples such as [87, 88] which discuss not only at the values of ns and ps but also how the distributions of choices (the mechanics of the application of the d-1 devices in our diagram) move with assignment of cultural practices to individuals when a village might be subdividing. There are thus many things that can be better understood when using proper statistics (here, using SNSK), to forecast population average statistics, is allowed.
[48] also discussed that some combinations of possible histories might be unable to combine with one another, so it may be that not all means of potential cultural evolution might be possible. There are probably less than 20 distinct forms of how kinship systems may be created (though there may be thousands of cultures with distinct languages in which they might be expressed); and most of those systems have structural numbers at or well under s = 16. Thus not all combinations of possible cultures create a lattice whose top element creates a lattice whose top-group order is at or under s = 16. Empirically therefore there may be no such systems. Another way to state this is that there may be sets of possible histories, not all of which can be allowed to find each other, from within that particular set of histories. That result may create changes among histories in which some ranges of values of n(t) and of p(t) – and thus their consequences in predicting r(t) (and thus from Equation 4, R(t)), might not be allowed. The homotopy of these systems may therefore tell us a lot on which kinds of cultural systems might evolve into each other, and which, if any, might not evolve.
Many ethnographic studies discuss each cultural system as if there is only one history present in that population. In many ethnographic papers, therefore their discussion does not talk of “probabilities” that a culture is in some specific history; they assume a specific history, so no probabilities are needed. Applications of the same history at each instance of time also may imply that there is no change in demographics of the population: if the same structural number repeats, then the predictions of n(t) and p(t) do not change; so the forecasts remain at n(t) = ns and p(t) = ps; see also [47]. But when probabilities are needed (i.e. that more than one history be present in a society) then in [48] the probabilities use Pauli coefficients; this is used simply because complex Hilbert spaces simplify following specific paths.
The forms of mathematics found in Equations 1 through 4 also yield non-commutative forecasts. While some of our equations look like similar forms in quantum analysis, our results are not equivalent. One version of quantum mechanics [90, 91, 92, 93] uses a “consistent histories” approach, in which the same history is consistently followed in each generation of a descent structure. This approach defines a descent map (called “descent” in quantum theory as well), which, like the descent map of genetics or cultural theory, is a partial order. In physics, the physical object in each instance of t + 1 is a copy of the same history as in time t; only its momentum or location may have changed. Changing whether we measure first momentum or first location causes the problem of uncertainly in physics, despite the assumed consistency of the rules. But in cultural theory the objects at t + 1 are descendants of the objects at t; the members of t + 1 are distinct objects (distinct pairs of offspring), not the same objects as assumed in physical theory. [48] found that when objects in culture theory are non-commutative, our equations forecast r(t) ≠ 0 and thus also that we can predict if generation growth (or decline) occurs. Thus the differences when finding results in cultural theory are directly computable. Thus, while Equations 1 through 4 are based on non-commutative cultural theory, and we therefore can get significant changes in values of e(t), n(t) and p(t) over time, but we do not find uncertainly in cultural theory.
7. Forecasting evolution.
The well-known evolutionary biologist Wilson published his most current book, Genesis [94], in which the title apparently intends to forecast the next stage in evolution of life. It is apparent even from a sympathetic reviewer [95] that Wilson reaches no such conclusion. But Wilson does what an evolutionary biologist specializing in social insects might do: he uses the long history of evolution of social insects to “model” what may happen next with the much shorter and later span of evolution of humans.
In our own discussion in Parts 4 and 6 we also discuss the possibility of forecasting. Can we use the notion of surjection to assist prediction in biological systems? Pauling [97] in 1940 used the mathematics of the chemical bond for description of the molecules used in evolution. Petoukhov [98, page 26] says that Pauling’s “… presentation form is based on symmetric matrices, … Symmetrical matrices are related with the theory of resonance of L. Pauling …”. Part 4 of this paper tells us that any configuration that follows the constraints of Part 4 can also create symmetrical matrices (in fact, mathematical groups) that may cause evolution, so long as they follow the group requirements in Part 4.
The proof of that prediction that would be to simply demonstrate it has occurred, which it has (see also citations of Part 4) and that it has been predicted. To the knowledge of this author, using symmetrical configurations to describe biological evolution was first described by the mathematician Schroeck [89, pages 223 – 253], in bats. [89] is not describing either the loci nor the alleles of evolution, it is demonstrating the results. [89] showed that bats identified other objects in flight by computations inside the bat, and when the speeds of object found by the bat became fast enough, by using quantum mechanical devices inside the bat to identify and follow the objects tracked. As the mechanisms of the other flying animals became fast enough, the limits (and result) of their locational devices was that “Detailed analysis … shows that bats perform at the quantum limit of uncertainty relations …”. [89, page 252-253] continues by proposing that
“… we observe that joint time/frequency spectrograms are being used as a standard analysis procedure in studying biological and social systems. We list the ‘pictures’ of bird songs in many popular bird identification manuals, as well as the identification of vocal expressions of stump-tailed macaques … as examples.”
In fact, [89] has stated that the biological results are determined by the requirements of the physics. There is actually nothing unique in this, except it shows that “simply” the mechanics allowed by relations allowed by Part 4 have that result. We give other examples below.
[95] says [94] might better have compared the evolution of social insects to the evolution of human communications from understanding kinship (which is the opposite of what Wilson asserts). Read [96] shows that the (verbal!) notions of human kinship analysis derive perhaps 50,000 years ago in descriptions of human society. Dinosaurs, including the first birds, began many millions of years ago to use verbal communication with each other, which is also a primary feature of human evolution and human society. Indeed if humans did not have verbal communication, how could we write the sections of this paper describing human ability to describe human society using kinship terminologies – which are part of human communication systems – and to then discuss the role of those using mathematical groups to understand the demography of human societies? But we have also found from the example described by Schroeck, that biological evolution is based on physical mechanical devices. In much of physical theory, and certainly for forming DNA or RNA molecules, forecasting future conditions are in large part due to their symmetry, given their required mathematical groups.
So let us restate the issue here: do the possible alleles that may be formed under mechanics allowed by our Part 4 citations, necessarily cause specific forms that define future evolution? That is not how we normally state finding potential evolution. It places the computations of Part 3 as demonstrating the paths of particular results; but requires that only things allowed by what Part 4 references allow to create, that determines the eventual results of evolution. Consider the results Hirschleifer [99]. [99] showed that the logic of economic evolution (in effect, classical physical dynamics, as used in the computations of the Part 3 predictions) could allow biology to favor “sacrificial” individuals—individuals who help other members survive by themselves dying to save other members of the species, to assure that; thus “altruistic evolution” was thus found to be favored by Part 4 devices. Much of our understanding of how Darwinian theory explains human culture, and how human creativity using mental processes causes social evolution, are due to Hirshleifer [99]; see also [100].
Therefore also biological evolution, as summarized by [89], allows us to believe that human logical abilities (a result of biological evolution) can thus also cause human “cultural” evolution. Methods of how communication can occur [101] in biological evolution are very diverse. [101, Chapter 12] includes tweaks as animals move, which are very different from human or other animal verbal communications [101, Chapter 13 and 14]. Once some biological entity has communication capability, it is only a matter for time before some individual(s) of that species can use them to create languages, including mathematics; see Ezhkova [102, 103]. This is also proven since such things are already widely present in diverse species; certainly in humans, and recent work shows birds [104 and other citations] verify that other species may have at least parts of it. Kauffman [105, 106] argues that evolution should also look for means of communication among species, and says that “simple and complex systems can exhibit power full self-organization”. But that “… no body of thought incorporates self-organization into the weave of evolutionary theory” [105, page vii]; see also Mayr and Provine [107]. But Part 4 was formed by understanding that we have a surjection; since surjection also implies the mathematics of group theory (Part 4), understanding surjection incorporates “self-organization” by finding necessary use of mathematical groups.
Human logic (also a product of biological evolution) can already forecast results of much of the mathematics of physics. The human brain (also a product of biological evolution) can forecast future versions of many domesticated crops and animals; so have other species that have “tended” crops. Then why can’t humans forecast (indeed create) their own cultural and biological evolution? See also [108].
Hirshleifer [99] found that biological evolution can occur when what are sometimes called “self-sacrificing” individuals in a species take actions that improve the survivorship of the species, but do not cause that individual’s own genes to be passed by his own evolution. Many events occur in species using commonly allowed actions of individuals with other members of the species, both with or without a form of communication; and many of those allow some individual actions to favor the whole species, both with and without “self-sacrifice”. The many entries in Silk’s [109] review (per advice of Sherwin [110]) give examples over many species. [109, page 540] summarizes:
“Here, I review published information about the effects of intraspecific variation in group size, group composition and the nature of social bonds on the reproductive performance of females in mammalian species. Although much of the work on social cognition has focused on primates, I have expanded the taxonomic scope of this review beyond primates for several reasons. First, there is no particular reason to think that the evolutionary consequences of sociality in primate females are different from the evolutionary consequences of sociality in other mammalian taxa. Primate females share basic features of their reproductive biology with females in other mammalian taxa, and face many of the same tradeoffs between the costs and the benefits of living in social groups. Second, some valuable information about the proximate and ultimate consequences of sociality come from experimental studies that would be impractical to conduct on primates. Third, there is a vast literature on mammals which provides a rich source of evidence about the adaptive consequences of variation in sociality.”
Silk thus says that while her focus (from more than 6 pages of citations on many species) is on primates, primate actions are broad enough that they represent many species. Silk actually cites diverse species including rats, mice, goats, monkeys, male baboons (alone), adult male baboons and lactating females, cetaceans, rhodents, other primates, ungulates, carnivores, insectivors, and others. [104] was an example of how birds (in that case, parrots) may have logical facilities, in some ways similar to humans; and bird sounds, not just the possible included logic, often directly affects selection of which specific individuals mate [111, 112]. In our discussion in Parts 5 and 6 especially, using human communications, there is thus also no reason to believe that our reference there to humans (primates!) limits our own conclusions. It also relates to [51] which demonstrated examples from literal (non-genetic) communications such as by human languages, and from [52] prediction of genetic inheritance sequences, by the same analysis as used for understanding human languages. Our Part 3 measures are usually based on individuals, but inheritance can also occur in a population even when some individuals exhibit the desired behavior, by their actions, in some form, allow other offspring than their own to value from their own genetics. The biological mechanics of SNSK devices in Parts 5 and 6 also show an example of communication among individuals but that can have consequences we can measure and verify on populations (including genetic) statistics. That is, Part 3 measures should be expanded to use population-based measures., to understand how mechanisms allowed by Part 4 can become more general in an evolving population.
8. Use of Entropy.
So far what we know from the classification of inheritance as a surjection, is that all forms of alleles must come from the mechanics allowed by Part 4, that is, to be consistent with physical theory and especially to be framed by particular sets of mathematical groups; and that each new offspring can be unique in at least one (but possibly many) ways from other offspring of the same species. Physical mechanics (Part 4) allows us to describe the objects on which evolution can take place, while genetic statistics (Part 3) may describe means of demonstrating evolutionary effects in actual use. We need to understand both forms of prediction, and to understand how they relate to each other. But biological evolution may only occur only in specific directions implied by what Part 4 devices can create and allow.
Chanda and colleagues [113, 114, 115, 116] thus show the current state of population based measures on evolution. We do not summarize those somewhat later adaptations, but instead summarize the origins of population-based measures. [113] tells us that the originator of that work was Gatlin [117, 118, 119, 120, 121]. Gatlin assessed genetic relatedness based on allele frequencies in populations, based on entropy; our summary of the derivation of Gatlin’s measure, stated shortly below, follows from [121]. She finds this by measure called RN2; we repeat her derivation below. Assessing RN2 also reflects if the species DNA or RNA has contributions from either or both “self-sacrifice”, or from other forms in which individuals may contribute to preserving the species but not, by their immediate physical actions, changing the DNA. For example, some individuals may act now (such as by helping avoid predators); and this when those individuals reproduce they also perpetuate their DNA or RNA.
The RN2 measure is based on entropy, but also related to measures of communications of Shannon [122]. Gatlin thus also shows measuring that RN2 responds to Lotka [123 page 147]:
“… in the struggle for existence, the advantage must go those to organisms whose energy-capturing devices … are most efficient in directing available energy into channels favorable [to] the preservation of to the species”;
and Lotka [124 page 153] in which nature “… has long realized that the principle [of natural selection] is capable of such application; …”. Both Lotka (and also von Newman [121]) therefore view evolution as creating the most efficient devices that the mechanics of Part 4 citations allow. But Gatlin [121] shows it also relates to communications, as implied by entropy. [120, page 295] concludes:
“It defines a fundamental entropy mechanism for increasing the fidelity of a message which we observed in the genetic language and in human language. We are led into the consideration of a principle which is the confluence [of] Darwin's principle of natural selection and …[the] second theorem. This is an organizing principle in contrast to the disorganizing principle of thermodynamics. And finally, we are left with the rather satisfying explanation that it is the second theorem of information theory rather than the second law of thermodynamics which has given the evolution of life its unique direction.”
We now briefly summarize how to derive Gatlin’s RN2 measure. From [121] Gatlin’s assumes we have a finite alphabet A of size a (for genetics, a = 4 items, the DNA objects {A, T, C, G}), or
- A = {xi, I – 1 … a}
For each a there is a probability 0 ≤ pi ≤ 1, SUMpi = 1. The entropy of the source is then
- H1 = - K SUM Pi log pi.
In Equation 6 the index K is usually (and here) taken to be K = 1, and the log is binomial; that is, Gatlin is discussion entropy by bits of information. If all ai have equal probability, then H1 = log a. She then defines the maximum entropy due to a divergence of equiprobability of all i, as
- D1 = log a - H1
To analyze the divergence of the sequence, she then defines for each n,
- SUMn = {XjXi . . . Xn : i, j . . . n = 1, a}.
If the letters in the n-tuple are independent of each other, then
- H Ind n = - SUMi SUMj . . . SUMnPiPj . . . Pj log PiPj . . . Pn
and:
- H Ind 1 = n H1.
Let m be the memory of a Markov source. If m = 1 then the probability of occurrence of a given letter depends only on the letter preceding it in the sequence. Which means the entropy of Sn is given by:
- H Dep n = - SUMi SUMj . . . SUMnPiPij . . . P(n-1)n log PiPj . . . P(n-1)n
where Pij is the one step Markov transition probability from letter i to letter j. Now require SUMj Pij = 1 and SUMi PiPij = 1, in which case
- H Dep n = H1 + (n – 1)H1m
where
- H1m = - Si Sj PiPijlogPij.
Gatlin then notes that this is just the entropy of a first order Markov source. If m = 2 then, after one simplifying steep,
- H Dep n = H1 + H1m +(n – 2) H2m
where
- H2m= - SUMi SUMj SUMk PiPijPijklogPijk
which she then generalizes to be:
- H Dep n = H1 + H1m + H2m + . . . H(m -1)m+ (n – m) Hm.
Following [125] then since H m + 1 M ≤ H m M then H Ind n ≥ H Dep n.
She then defines the divergence from independence as:
- D2 = lim(n to infinity)(1/n)( H Ind n - H Dep n).
Thus from Eqn. 10 that lim(n to infinity)(1/n)H Ind = H1, and if we assume m << n (because molecules of relevance here are very long) then
- lim(n to infinity)(1/n)H Dep n = HmM.
Therefore:
- D2 = H1 - HM.
Thus, the maximum entropy state is thus
- Id = D1 + D2.
She now wants to show how this relates to Shannon’s [122] definition as
- R = 1 – Hm/ log a.
From Eqn. 7 and 21 allows that:
- R = (D1 + D2)/log a, or R = Id /log a.
Which allows to define both
- RD1 = D1/(D1 + D2) = D1/ Id = D1/(R log a)
- RD2 = D2/(D1 + D2) = D2/ Id = D2/(R log a)
so that RD1 + RD2 = 1. And thus the total amount of departure from randomness is characterized by the measure RD2.
Thus [121, page 85] Gatlin concludes (below we use D1 in place of [121] text D1, and D2 for the [121] text D2):
“As D1 increases, the potential message variety is rapidly reduced. In the limit, maximal D1 characterizes the monotone, the absolute zero of information theory with no message variety. … As D2 is increased, the potential message variety also declines, but at a slower rate. However, the increase of both D1 and D2 contributes to the reliability and the fidelity of the message as measured by the R value. … [thus] the most efficient encoding for a given value of R is that with the smallest D1 and the highest D2, that is, the highest RD2. This achieves the maximum potential variety without loss of fidelity …”.
Part of the proof that Gatlin’s ideas, involving both entropy and communication, and her (and thus Chanda’s) measures, may predict how biological evolution may occur, has been assessed in [113, 114, 115, 116], in the work of Sherwin [110, 126, 127] and in [128]. In both [126, 128] one sees that measures like those of [121] can be and have been suitably computed by others. The time periods over which each measure occurs in a generation can be much longer than what often occurs in simply measuring individual physical reactions; see [110] Table 3 for the time period of each measure.
In [126, page 540] after study of simulation of fitness for one trait in bottlenose dolphins, the authors observe: “… not only that a female fitness trait is influenced by both genetic and social effects, but that these effects on the evolution of fitness traits are strongly intertwined.” That is, social interactions, such as those widely found by [109], or from applying human kinship terms, or the diversity by which individuals care for offspring (even if not necessarily their own biological offspring, as many species identified in [109]), show that interactions of individuals of a species, which do not by that action transmit their own DNA to some immediately affected offspring, may still get their DNA transmitted, whether by self-sacrifice, or by the individual in other ways relating to offspring not her own. Thus we can get increases in Gatlin’s RD2 simply by expanding the number of individuals that form beneficial interaction with offspring of other offspring in the same species, from any beneficial trait, if that trait is allowed by Part 4 mechanisms.
Thus [120, Page 295] concludes that:
“… we see that D2 is not just another evolutionary index which can distinguish between vertebrates and lower organisms. It is an entropy function. It extends the concept and endows it with structure. It defines a fundamental entropy mechanism for increasing the fidelity of a message which we observed in the genetic language and in human language. We are led into the consideration of a principle which is the confluence of Darwin's principle of natural selection and … [the] … second theorem. This is an organizing principle in contrast to the disorganizing principle of thermodynamics. And finally, we are left with the rather satisfying explanation that it is … information theory rather than the second law of thermodynamics which has given the evolution of life its unique direction.”
Note that RD2 is directly driven by D2.
The efficiency results of Lotka or von Neuman are thus not the only drivers of evolution. Measurements of [117, 121] are also implied by surjections: they maximize the ability of any of Part 4 physically allowed actions to become part of the DNA of a species, using the basic rules of physics. Gatlin shows how to trace and track the presence of those devices. [120] appears in [129]. Many of the other articles in [129] - especially but not only [130] - are closely related to Gatlin’s results. Gatlin’s 1972 book [117] is still a good introduction to more modern treatments of what we now call “bioinformatics”, including much more recent texts such as [131, 132]; [117] even notes the mathematical group theory of physics. It is odd therefore, that work such as [133] in 1982, or [105, 106] published after 2000, and others, often claim to be the first to assess the relation of genetics to entropy or communications, though [133] does cite Gatlin’s proposals without fully recognizing their results. More recent work [134] cites Gatlin on the genetic equivalence to maximizing information and the use of energy.
Gatlin’s results, stated in nearly exactly the notation we summarized above, is the foundation for the properly titled text Evolution as Entropy [135] by Brooks and Wiley. [135] page 3 explains the need for their work, as solving these four objectives:
“1. Evolutionary theory has never fully come to grips with apparently lawlike behavior in biological systems. 2. Developmental biology has not been successfully integrated into the theoretical framework [per this author: of theoretical physics]. 3. Existing evolutionary theory has failed to provide a rationale for the existence of the higher taxa (groups of species produces by descent) that is consistent with our knowledge of phylogeny and population genetics. 4. Existence evolutionary theory has failed to provide what we would consider to be a robust explanation of the relationship between form and function.”
To solve those issues, [135] then develops the mathematics to fill those voids, and in doing that uses exactly the explanations from Gatlin we summarized above. In [117], much of the text after developing the mathematics, is discussion by Galvin of those four issues, as well as discuss the time periods for and sequence of evolution.
9. Summary
Our subject here, that inheritance is a surjection, is simply stating and analyzing a classification used for some objects in math. That classification is not usually used to evaluate evidence as well, it simply classifies. Our summary says that inheritance, whether biological or cultural, as a surjection, also says that we must measure results on an entire population, not just individual outcomes, to understand and predict the evolution which can ensue. It leads us to the conclusion states here: knowing the methods is a surjection, also leads us to understand that both cultural and physical inheritance, are a necessary part of physical evolution. We used some theorems on surjection to interpret this result. We must allow both for both the uniqueness of individual new offspring in a population, while knowing certain common features must accompany creating evolution in any species. For cultural evolution, this also affects measures of average family size. For biological evolution, the limits to forecasting evolution are the biological limits imposed by our Part 4 articles, while their relation to future evolution is subject to the RD2 measure created by Gatlin. (There are also other differences in what can be forecasted for cultural vs biological evolution, not discussed here.)
Gatlin’s work is based on information theory, which she shows is in equivalent to entropy. Sherwin [110] expands Gatlin’s result, by showing that evolution must also be evaluated with its ecology. [110], citing [136], says we must combine four “common features”: innovation, transmission and replication, movement, and adaptation, in part by entropy-based measures. [136] is correct, but because it is often restating results per the mathematics in [135]. Thus Sherwin and colleagues [127] contains many articles that demonstrate that genetic entropy is indeed significant. Thus [110, page 8] says
“… adaptation included not only self selection but interaction with all other information processes such as behavioral science avoidance of harm … or other molecular interactions”.
That is, behavioral actions of individuals also can affect evolution, even if those are not directly found by measures of Part 3; but the addition to Part 3 by study of the RD2 shows those effects on an entire species, and their organization. Thus after developing the measure RD2, in [117] are detailed examples on diverse species, and on distinct organization of species.
One can thus compare [110] in its Table 3 forecasting notes (on time periods for measuring evolution), to the a wide list of possibilities to forecast evolution as presented in [95] (but which is not sure which if any may be right); which in turn is to substitute for the lack of any forecasting by Wilson [94] despite the implication of the title of his work. [110] Table 3 is shorter, more complete, covers only specific items that relate to evolution, and cites the physical mechanics of what may occur and their time-frames. [136], citing the work of [122] (which Gatlin also cites), looks to improve the specification of time-frames for evolution. [136] does not affect the derivation of Gatlin’s RD2, so is not further discussed here; but see also discussion of Figure 2 below.
The fact that inheritance is a surjection thus also helps us find that both biological and cultural evolution are part of the same subject: physical science. For example, understanding the implications of measuring RD2 also implies genetic measures of phenotypes that are demonstrated in animal behavior, not simply dimensions of some physical object. But even in 1972 the existing math and its implications were not often discussed. Gatlin asked why a broad understanding of why “conditional probabilities” for inheritance was not already well known. [117, page 44] says:
“The conditional probabilities … represent the first experimental measurement which can tell us something about the informational properties of the total base sequence of any large DNA molecule. … comparable in importance to the early measurements of the spectrum of the hydrogen atom, which aided the development of quantum theory. … But the nearest neighbor experiment rests on the shelf, largely forgotten and unappreciated in the information explosion that is rocking the biological world today.”
The text above from [117] is from a section in which Gatlin discusses what she believes is the most fundamental mathematics of inheritance: ergodicity. Ergodic studies are on stability of classical physics, but which thus also allows for existence of biological evolution. Because ergodic studies began well before Gatlin’s work of the 1960’s and 1970’s, it has its own directions, and finds results independently of what evolutionary scientists are doing. But when it does, it finds things close to what Gatlin found. For example, in 2015, [138] asked if there are “ergodic limits to evolution”. [138] created Figure 2 below (which is a copy of Table 2 from [138]); it compares physical theory as discussed by authors on ergodicity in the left column, to evolutionary theory in the right column. [138] does not cite Gatlin’s work, but compare the results: 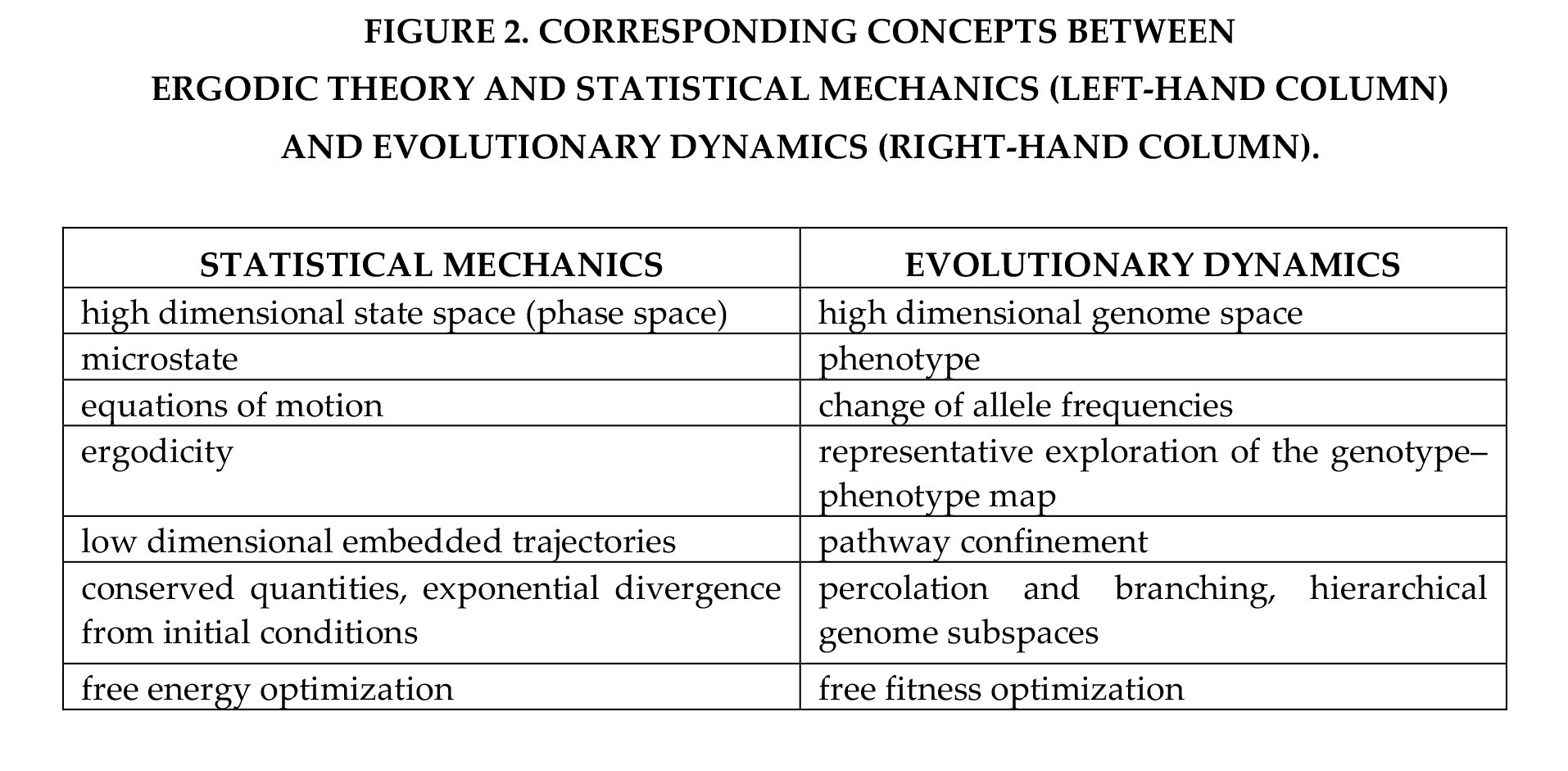 Compare the “evolutionary dynamics” column in Figure 2 to results from Gatlin. Gatlin’s work assumes a high dimensional genome space (see our note after Equation 17); her study is of observable effects of evolution, that is, phenotype – we have compared only a small part of the forms of evolution she can compare by citations in [109]; her development of RD2 is of the changes of allele types in the genotype-phenotype maps; she is definitely studying possible branching or confinement of spread of alleles; and she deals with the optimization of fitness. Gatlin has thus correctly cited ergodicity as a guide for her developments. [117], published in 1972, is still a current introduction to the physics summarized in our Part 4, though the sources cited in Part 4 are published in or after 2000. It seems clear from Figure 2 that ergodic theory has almost certainly found many results that support the work of Gatlin, or the more comprehensive vision of Sherwin; a survey on that topic by cognizant mathematicians would be very useful.
Compare the “evolutionary dynamics” column in Figure 2 to results from Gatlin. Gatlin’s work assumes a high dimensional genome space (see our note after Equation 17); her study is of observable effects of evolution, that is, phenotype – we have compared only a small part of the forms of evolution she can compare by citations in [109]; her development of RD2 is of the changes of allele types in the genotype-phenotype maps; she is definitely studying possible branching or confinement of spread of alleles; and she deals with the optimization of fitness. Gatlin has thus correctly cited ergodicity as a guide for her developments. [117], published in 1972, is still a current introduction to the physics summarized in our Part 4, though the sources cited in Part 4 are published in or after 2000. It seems clear from Figure 2 that ergodic theory has almost certainly found many results that support the work of Gatlin, or the more comprehensive vision of Sherwin; a survey on that topic by cognizant mathematicians would be very useful.
One current writer [139, at page 156] says that since [117] discussed “only” DNA, the work is “out-dated” since it does not recognize genetic sequence order in individual DNA. But [117] Chapter 9 does discuss genetic sequence. [117] also discusses how RD2 has also been measured on RNA -- derivations for RNA are cited in [117] Table 4 on page 76, and the derivations for measurements on RNA are discussed in the footnote article to Table 4. There is nothing in [139] that finds anything wrong with the derivations or applications of [117, 120]. [139] is simply wrong. Aa proof of this, a reconsideration of Gatlin's work has been published in 2012, [140] by Ivan Erill. Erill considers critiques of Garlins such as by [139], shows why those critiques are wrong, rederives Gatlin's work in more current terminology, derives additional useful measures on species using Gatlin's definitions, and thus helps further prove that entropy is indeed a major source of evolution.
One of the largest difficulties of ending this article is that it has found the incredibly significant work of Gatlin, but to my knowledge her work stopped being published in 1976. From her obituary [141], she lived another 41 years. [117], in Chapters 4 through its end, discusses many issues on computing and finding results from her measurements. It is not clear what Gatlin thought about [135], which was done in the period when Gatlin was not publishing work. It was clear in her work in [117] that she believed her concepts were very productive, yet needed more work. With the vast improvement in computers and mathematics since then, more can now be produced; witness Figure 2 and reference [140].
In Part 8 we began with discussing Wilson seeking but not producing, forecasts of future evolution, including of humans. In the final two paragraphs of [117] Gatlin tells us:
“We often hear the cry in our age that science is for our destruction. That is half-truth. Science is also for our salvation. Science has simply forced man to face himself … It is time for us to take the helm and accept the responsibility of shaping our own evolution and destiny.”
Gatlin clearly believes her work on evolution will help force that. She has provided one of the foundations for why biological inheritance is a necessary result of normal physical process. One hopes Gatlin’s fundamental work can become more openly discussed.
References
- Grimaldi, R. P., Discrete and Combinatorial Mathematics. 1989. Addison Wesley, Reading Ma.
- Hildon, P.; Peterson, J.; Stiger, J. On Partitions, Surjections and Stirling Numbers. Bulletin of the Belgian Mathematical Society; Belgian Mathematical Society: Brussels, Belgium; 1994 Volume 1, pp. 713–735.
- Schadach, D. “A Classification of Mappings”, reprinted in Appendix 2, Ballonoff, P. Mathematical Theory of Culture, Austrian Society for Cybernetic Studies Monograph No. 40. 1987
- Stanley, R. P. Enumerative Combinatorics, Volume 1, Second Edition, 2012, Cambridge University Press, Cambridge
- Radzevilavicius, A. L and N. W. Blackstone, “The evolution of individuality revisited”, Rev. 2018, 93, pp. 1620–1633.
- Zheng, W., Zhao, H., Mancera, E., Steinmetz, L., Snyder, M., “Genetic Analysis of Variation in Transcription Factor Binding in Yeast”, Nature, published online 17, March 2010.
- Mendel, G. Experiments in Plant Hybridisation, 1865, reprinted 1965 with introduction, Harvard University Press, Boston
- Bernstein, S. “Demonstration mathematique de la loi d’heredite de Mendel”, 1923a, Rend. Sci. Math., Pt. 1, Vol. 177, 528 – 531.
- Bernstein, S. “Principe de stationarite et generalisations de la loi deMendel”, 1923b, Rend. Sci. Math., Pt. 1, Vol. 177, 581 – 584.
- Fisher, R. A, The Genetical Theory of Natural Selection. Oxford University Press, Oxford.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part I), Transactions of the Cambridge Philosophical Society, January, 1924, Vol, 23, No, 2, pp. 19-41.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part II), Biological Reviews of the Cambridge Philosophical Society, October, 1924, pp. 158-163.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part III)," Proceedings of the Cambridge Philosophical Society, October, 1926a, Vol. 23, po. 363-372.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part IV), Proceedings of the Cambridge Philosophical Society, October, 1926b, Vol. 23, pp. 607- 615.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part V), Proceedings of the Cambridge Philosophical Society, October, 1926b, Vol. 23 pp. 838-844.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part VI), Proceedings of the Cambridge Philosophical Society, October, 1930a Vol. 26, pp. 220-230.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part VII), Proceedings of the Cambridge Philosophical Society, October, 1930b, Vol. 27, pp. 131-136.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part VIII), Proceedings of the Cambridge Philosophical Society, October, 1930c, Vol. 27, pp. 137-142.
- Haldane, J. B. S. “A Mathematical Theory of Natural and Artificial Selection” (Part IX), Proceedings of the Cambridge Philosophical Society, October, 1931, Vol. 28, pp. 244-248.
- Haldane, J. B. S. The Causes of Evolution, original 1942, republished 1990, Princeton University Press, Princeton
- Wright, S. Evolution and the Genetics of Populations: Volume 2, The Theory of Gene Frequencies. 1969, University of Chicago Press, Chicago
- Nei, M. Molecular Evolutionary Genetics, 1987, Columbia University Press, New York
- Crow, J. F and M. Kimura, An Introduction to Populations Genetics Theory, 1970. Harper and Row, New York.
- Provine, W. B. The Origins of Theoretical Population Genetics, 1971, republished 2001, University of Chicago Press, Chicago
- Provine, W. B. Sewall Wright and Evolutionary Biology, 1986, University of Chicago Press, Chicago
- Lewontin, R. C. The Doctrine of DNA, 1992, Penguin Books, London
- Ewens, W. J. Mathematical Population Genetics, I. Theoretical Introduction, Second Edition, 2000, Springer Verlag, New York.
- Rice, S. H. Evolutionary Theory: Mathematical and Conceptual Foundations, 2004, Sinauer Associates, Sunderland MA.
- Okasha, S. Evolution and the Levels of Selection, 2006, Oxford University Press, Oxford
- Dronamaraju, K. Haldane, Mayr, and Beanbag Genetics, 2011, Oxford University Pres, Oxford
- Petoukhov, S. V. “Matrix Genetics and Algebraic Properties of Multi-Level System of Genetic Alphabets”, NeuroQuabtatology, December 2011, Vol. 9, Issue 4, 799 – 820.
- Petoukhov, S. V. “The degeneracy of the genetic code and Hadamard matrices”, no date
- Petoukhov, S. V. “Matrix genetics, part 1: permutations of positions in triplets and symmetries of genetics matrices”. Institute of Physics. Serbia, 2013
- Petoukhov, S. V. “Genetic coding and united-hypercomplex systems in the models of algebraic biology”, Biosystems, 2017 pp 31 – 46
- Petoukhov, S. V. “The Genetic Coding Systems and Unitary Matrices” 2019, a publication of the Institute of Machines Science, Russian Academy of Sciences
- Petoukhov, S. V. and Castro-Chavez, F. “A Tetrahedral Representation of the Genetic Code Emphasizing Aspects of Symmetry”, BioComplexity, 2012, Issue 2, Pages 1 – 6.
- Petoukhov, S. V and Z. B. Hu, “Generalized crystallography, the genetic system and biochemical esthetics”, Chem. February 2017, Volume 28, Issue 1, pp 239–247
- Petoukhov, S. V., E. Petoukhova and V. Svirin, “Genetic alphabetic alphabets, unitary matrixes and quantum-algorithmic genetics”, 2019, ToPME, IOP Publishing, pp 1 – 5.
- Hainen, P. C. “An octonion models for physics”, 4th Conference on Emergence, Coherence, Hierarchy, and Organization (ECHO 4), Denmark, 2000.
- Rakocevic, M. “Golden and Harmonic Mean in the Genetic Code”, TABIX, Serbia, 2013.
- Khrennikov, A. and A. V. Kozyrev, Replica procedures for probabilistic algorithms as a model of gene duplication. arXiv:q-bio/1104.2893v1 original 14 May 2011, download version of November 13, 2018.
- Khrennikov, A. and A. V. Kozyrev, Genetic code on the dyadic plane. arXiv:q-bio/070107v3 original 2 November 2007, download version of August 27, 2018.
- Khrennikov, A. Hyperbolic quantum mechanics. arXiv:quantu-ph/0101002v1 original 21 December 2000, is the version of July 18, 2018.
- Khrennikov, A. and A. V. Kozyrev, p-Adic numbers in bioinformatics: from genetic code to PAM-Matrix, arXiv::q-bio/0903.0137v3 original 4 April 2009, downloaded version of November 20, 2018.
- Dragovich, B and A. Dragovich, A p-Adic Model of DNA Sequence and Genetic Code. arXiv:q-bio/0607018v1 12 July 2006
- Rakocevic, M. M., The Cipher of the Genetic Code, Biosystems 171 (2018) 31 – 47.
- Ballonoff, P. “Progress of Mathematical Cultural Theory“, 2018-A, pp. 1-18, Mathematical Anthropology and Cultural Theory, Letters and Reviews to MACT. mathematicalanthropology.org
- Ballonoff, P. “Paths of Cultural Systems”, Entropy, 2018-B, Volume 20 (1) pgs. 1 – 14.
- Macfarlane, A., “Analysis of Relationships of Consanguinity and Affinity” in Journal of the Royal Anthropological Society 1882 Vol 12 pages 46 – 63.
- Ruheman, Barbara. “A method for analyzing classificatory relationship systems” in Southwestern Journal of Anthropology 1945 1 pages 531-576
- Petoukhov, S. V. “Structural Connections between Long Genetic and Literary Texts”, a publication of the Institute of Machines Science, Russian Academy of Sciences, 2019.
- Vaz, R. M. “Relatives, Molecules, Particles”, Mathematical Anthropology and Cultural Theory, 2014, Vol. 7 No. 1, pp. 1 – 157.
- Weil, A. 1947 Appendix to Claude Levi-Strauss, 1947.
- Claude Levi-Strauss 1947 The elementary structures of kinship (in English from Beacon Press, Boston 1969)
- White, Harrison. An Anatomy of Kinship, Prentice Hall, New Jersey. 1963
- Liu, Pin-Hsiung. “Formal Analysis of Prescriptive Marriage System: The Murngin Case”, in VIII Congr. Anthropolo. Eth. Sci., Vol II Ethnology, 1968, pages 90 – 92.
- Liu, Pin-hsiung, Murngin: A mathematical solution, Institute of Ethnology. Academia Sinica, 1970, Monograph ser. B, no. 2)
- Courrege, Philippe. “Un Modele mathematique des structures elementairs de parente”, in L Homme Volume 5 No 3 – 4, pages 248 – 290, translated to English by D. Read as pages 289 – 338 in Ballonoff, P. A. (ed.) Genetics and Social Structure, Dowden, Hutchinson and Ross, Stroudsburgh Pennsylvania (1974).
- Gould, Sydney and D. Kronenfeld New System for the Formal Analysis of Kinship University Press of America. 2000
- Greechie, Richard, and Martin Ottenheimer. “An Introduction to a Mathematical Approach to Kinship” pp. 63-85 in Genealogical Mathematics (P. Ballonoff’, ed., Maison des Sciences de l’Homme, Paris, 1974
- Harris, T. R., “From Relations to Groups: A Formal Treatment of the Underlying Logic of Some Group-Theoretical Models of Kinship” pp. 85 -109, in in Genealogical Mathematics (P. Ballonoff’, ed., Maison des Sciences de l’Homme, Paris. 1974.
- Gottscheiner, A. On some classes of kinship systems, I: Abelian systems. In Mathematical Anthropology and Cultural Theory, 2008; Volume 2, pp. 1–10.
- Gottscheiner, A. On some classes of kinship systems, II: Non-Abelian systems. In Mathematical Anthropology and Cultural Theory; 2008; Volume 2, pp. 1–10.
- Rauff, James R. “The algebra of marriage: an episode in applied group theory” (BSHM Bulletin: Journal of the British Society for the History of Mathematics, 2016, 31:3 pp. 230-244)
- Cargal, James pp. 157-168 “An Analysis of the Marriage Structure of the Murnguin Tribe of Australia” (1968 Behavioral Sciences 23)
- Tjon Sie Fat, Franklin, “Circulating connubium and transitive ranking: a second solution to Leachs problem”, in Bijdragen tot de Taal-, Land- en Volkenkunde 139 (1983), no: 1, Leiden, 140 - 151
- Tjon Sie Fat, Franklin, “Age Metrics and Twisted Cylinders: Predictions from a Structural Model”, American Ethnologist, Vol. 10, No. 3 (Aug., 1983), pp. 585-604
- Tjon Sie Fat, Franklin “On the Formal Analysis of ‘Dravidian’, ‘Iroquois’, and ‘Generational’ Varieties as Nearly-Associative Combinations” pp. 59-93 in Tjon Sie Fat F.E., Godelier M. editors, Transformations of Kinship. Washington DC and London: Smithsonian Institution Press. 1998
- Tjon Sie Fat, Franklin, Representing Kinship: Simple Models of Elementary Structures, (Thesis) 1990 Leiden.
- Tjon Sie Fat, Franklin, et al, “On Mathematics in Structural Theory” [and Comments and Replies], Current Anthropology, Vol. 21, No. 3, June, 1980, 386 – 391.
- Tjon Sie Fat, Franklin, et al, “More Complex Formulae of Generalized Exchange [and Comments and Replies], Current Anthropology, Vol. 22, No. 4 (Aug., 1981), pp. 377-399
- Read, Dwight, “The Generative Logic of Crow-Omaha Terminologies: The Thonga-Ronga Kinship Terminology as a Case Study”. Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 1, pp. 1 – 37.
- Read, Dwight, “Reply to Comments on The Generative Logic of Crow-Omaha Terminologies: The Thonga-Ronga Kinship Terminology as a Case Study. Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 8, pp. 1 – 62.
- Heady, Patrick, “Comment on D. Read ‘Generative Crow-Omaha Terminologies’", Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 2, pp. 1 – 8.
- Tjon Sie Fat, Franklin, “Comment on D , Read ‘Generative Crow-Omaha Terminologies’” Mathematical Anthropology and Cultural Theory, Vol. 12, No. 3: 1 – 10.
- Hamberger, Klaus, “Comment on D. Read ‘Generative Crow-Omaha Terminologies’ ", Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 4, pp. 1 – 9.
- Patrick, “Comment on D. Read ‘Generative Crow-Omaha Terminologies’", Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 5, pp. 1 – 4.
- Trautmann, Thomas R. and Peter M.Whiteley “Comment on D. Read ‘Generative Crow-Omaha Terminologies’ ", Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 6, pp. 1 – 12.
- de Almeda, Mauro Barbosa “Comment on D. Read ‘Generative Crow-Omaha Terminologies’", Mathematical Anthropology and Cultural Theory, 2018 Vol. 12 No. 7, pp. 1 – 23.
- Leslie, P. H. “On the use of matrices in population mathematics”, 1945 Biometrika 33: 183-212.
- Leslie, P. H. “Some further notes on the use of matrices in population mathematics”, 1945 Biometrika 35:213 – 245.
- Lotka, A, “Relation Between Birth and Death Rates” in Science 1907, 26(253):435-438.
- Duchamp, T., P Ballonoff, in Chapter 3 of Ballonoff, P. Mathematical Foundations of Social Anthropology, 1975. Mouton, Paris.
- Ballonoff, P. “Mathematical Demography of Social Systems” in Trappl, R. (ed.) Progress in Cybernetics and Systems Research Vol X. 1982, pages 101 – 112, Hemisphere Publishing Company, Washington.
- Ballonoff, P. “Mathematical Demography of Social Systems II”, in Trappl, R. (ed.) Cybernetics and Systems Research Vol, XI, 1982, pages 555-560, North Holland Publishing Co.
- Ballonoff, P. Mathematical Theory of Culture, Austrian Society for Cybernetic Studies Monograph No. 40.
- Ballonoff, P. Theory of Lineage Organization. American Anthropologist, New Series. 1983. Vol. 85, No. I, pp. 70 - 91
- Ballonoff, P. Structural statistics: Models relating demography and social structure with applications to Apache and Hopi. Social Biology. 20: 4, 421 – 426, .5, No. I, pp. 70 - 91
- Schroeck, F. Quantum Mechanics on Phase Space, 1996. Kluwer Academic Publishers, Dordrecht.
- Isham, C. J. “Quantum Logic and Decohering Histories”, 1995. arXiv:quant-ph/9506028.
- Isham, C. J. Lectures on Quantum Theory 1995, Imperial College Press.
- Sorkin R.D. “Space time and causal sets” in Conf. SILARG VI, 1990 Cocoyoc, Mexico
- Sorkin R.D. and D.P. Rideout “A Classical Sequential Growth Dynamics for Causal Sets” in Rev. D 61 024002 (2000) E-print archive gr-ge/9904062.
- Wilson, E. O. Genesis: The Deep Origin of Societies. 2019. New York: Liveright Publishing.
- Denham, W. “Sociality in E.O. Wilson’s Genesis: Expanding the Past, Imagining the Future”. In Mathematical Anthropology and Cultural Theory, 2019, Vol 14, No. 1, in press.
- Read, D. From past to present: the deep history of kinship. Chapter 6 in: Saqalli M., Vander Linden M., eds, Integrating Qualitative and Social Science Factors in Archaeological Modelling. Computational Social Sciences. Springer International Publishing. https://doi.org/10.1007/978-3-030-12723-7_6.
- Pauling L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, 2nd ed. Oxford University Press, London.
- Petoukhov, P., Petoukhov, S. Hyperbolic Numbers in Modeling Genetic. Phenomena Preprints2019, 2019080284 (doi: 10.20944/preprints201908.0284.v2).
- Hirshleifer, J. Economics from a Biological Viewpoint. Journal of Law and Economics. 1977, 20(1), 1–52.
- Hausken, K. “Jack Hirshleifer: A Nobel Prize left unbestowed”. European Journal of Political Economy Volume 22, Issue 2, June 2006, Pages 251-276
- d’Ettorre, P. and D, P. Hughes, eds. Sociobiology of Communication 2008, Oxford University Press, Oxford.
- Ezhkova, I. Self-organizing representations. 2005 Cybernetics and Systems 36(8): 861-875
- Ezhkova, I. The Principles of Cognitive Relativity, Rationality and Clarity: Application to Cultural Theory. 2004 Cybernetics and Systems 35(2-3): 229-257
- Pepperberg, I. M. The Alex Studies, Cognitive and Communicative Abilities of Grey Parrots. 1999, Harvard University Press, Cambridge.
- Hauffman, S. Reinventing the Sacred. 1993, Oxford University Press, Oxford.
- Hauffman, S. The Origins of Order: self-organization and selection in evolution. 2008, Oxford University Press, Oxford.
- Maye, M and W, Provine, eds. The Evolutionary Synthesis: Perspectives on the Unification of Biology 1980, Harvard University Press.
- Ballonoff, P. On the Evolution of Self Awareness, pp. 347 - 352 in Trappl, R. (ed.), Cybernetics and Systems Volume I, 2000, Austrian Society for Cybernetic Studies.
- Joan B. Silk*. 2007. The adaptive value of sociality in mammalian groups. Trans. R. Soc. B (2007) 362, 539–559. doi:10.1098/rstb.2006.1994. Published online 26 January 2007
- B. Sherwin, “Entropy, or Information, Unifies Ecology and Evolution and Beyond” Entropy 2018, 20, 727; doi:10.3390/e20100727
- Catchpole, C. K. and P. J. B. Slater. Bird Song, Biological Themes and Variations. Second Edition. Cambridge University Press, Cambridge.
- Marler, P. and H. Slabbeloorn. Natures Music, The Science of Birdsong. Elsevier Academic Press, Amsterdam.
- Chanda, P. PhD, “Information Theory in Computational Biology”, at 5th International Electronic Conference on Entropy and its Applications, 18 – 30 November 2019.
- Chanda, P., Lara Sucheston, Aidong Zhang, Daniel Brazeau, Jo L. Freudenheim, Christine Ambrosone, and Murali Ramanathan. “AMBIENCE: A Novel Approach and Efficient Algorithm for Identifying Informative Genetic and Environmental Associations With Complex Phenotypes.” Genetics Society of America, 2008, DOI: 10.1534/genetics.108.088542
- Chanda, P., Aidong Zhang, Lara Sucheston and Murali Ramanathan, 2009, “A two-stage search strategy for detecting multiple loci associated with rheumatoid arthritis.” Genetic Analysis Workshop 16, St Louis, MO, USA 17-20 September 2009, Published: 15 December 2009. See also BMC Proceedings 2009, 3(Suppl 7):S72 doi: 10.1186/1753-6561-3-S7-S72, available from: http://www.biomedcentral.com/1753-6561/3/S7/S72
- Chanda, P., Aidong Zhang, Daniel Brazeau, Lara Sucheston, Jo L. Freudenheim, Christine Ambrosone, and Murali Ramanathan. Information-Theoretic Metrics for Visualizing Gene-Environment Interactions. Am J Hum Genet. 2007 Nov; 81(5): 939–963. Published online 2007 Oct 3. doi: 10.1086/521878. PMCID: PMC2265645. PMID: 17924337.
- GATLIN, L. L. Information Theory and the Living System, New York, Columbia University Press, 1972
- GATLIN, L. L. "The information content of DNA." J. Theor. Biol., (1966), pp. 281-300.
- GATLIN, L. L. "The information content of DNA. II," Theor. Biol., Vol. 18 (1968), pp. 181-194.
- GATLIN, L. L. Evolutionary Indices. pp. 277 – 296, in Le Cam, L. M., Neyman, J., & Scott, E. L. eds, Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley and Los Angeles, University of California Press, 1972, Vol. 5.
- GATLIN, L. L. Information Theory, Molecular Evolution, and the concepts of von Neuman. pp. 81-97, In Goodman, M., et al (eds) Molecular Anthropology, Genes and Proteins in the Evolutionary Ascent of the Primates. 1976. Plenum Press, New York.
- Shannon, C. E. 1948. The Mathematical Theory of Communications. University of Illinois Press, Urbana, Ill.
- Lotka, A. J. Contribution to the Energetics of Evolution. N. A. S. 1922, Vol. 8, 147-151
- Lotka, A. J. Natural Selection as a Physical Principle. N. A. S. 1922, Vol. 8, 151-154
- Khinchin, A. I. Mathematical Foundations of Information Theory, New York, Dover, 1967.
- B. Sherwin, A. Chao, L. Jost, and P.E. Smouse. Information Theory Broadens the Spectrum of Molecular Ecology and Evolution. Trends in Ecology & Evolution, December 2017, Vol. 32, No. 12 https://doi.org/10.1016/j.tree.2017.09.012
- Celine H. Frèrea, Michael Krützen, Janet Manna, Richard C. Connora, Lars Bejdera, and William B. Sherwin. Social and genetic interactions drive fitness variation in a free-living dolphin population. PNAS, November 16, 2010, 107, no. 46:19949–19954. www.pnas.org/cgi/doi/10.1073/pnas.1007997107
- Skene, K. R. Life’s a Gas: A Thermodynamic Theory of Biological Evolution. Entropy, 2015m 17, 5522-5548; doi:10.3390/el7085522
- Le Cam, L. M., Neyman, J., & Scott, E. L. eds, Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley and Los Angeles, University of California Press, 1972, Vol. 5.
- Holmquist, R., Theoretical Foundations of Paleogenetics, pp 314-350, in Le Cam, L. M., Neyman, J., & Scott, E. L. eds, Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley and Los Angeles, University of California Press, 1972, Vol. 5.
- He, W. and S. Petoukhov. 2011. Mathematics of Bioinformatics. Wiley and Sons. Inc., Hoboken, N.J, USA.
- Mount, D. W. 2004. Bioinformatics, Sequence and Genome Analysis. Cold Springs Harbor Laboratory Press, Cold Springs Harbor, N. Y.
- Campbell, J. 1982. Grammatical Man: Information, Entropy, Language and Life. Simon and Schuster. LOCATION
- Matta, C. and L Matta. Notes on The Energy Equivalence of Information. Phys. Chem. A 2017, 121, 47, 9131-9135.
- Vellend, M. The Theory of Ecological Communities (MPB-57); Princeton University Press: Princeton, NJ, USA, 2016.
- Brooks, D. R. and E. O. Wiley. Evolution as Entropy. University of Chicago Press, Chicago. 1998
- O’Reilly, G. D., F. Jabot · M. R. Gunn, W. B. Sherwin. 2018 Predicting Shannon’s information for genes in finite populations: new uses for old equations Conservation Genetics Resources https://doi.org/10.1007/s12686-018-1079-z
- McLeish, T. C. B., 2015. Are there ergodic limits to evolution? Ergodic exploration of genome space and convergence. Interface Focus 5: 2015004 http://dx.doi.org/10.1098/rsfs.2015.0041
- Tame, J. R. H. Approaches to Entropy. Springer Nature, Singapore. 2019.
- Erill, L. Information Theory and Biological Sequences: Insights from an Evolutionary Perspective.pp. 1 - 28 in P. Deloumeaux and J. D, Gorzalka: Information Theory: New Research. Nova Science Publishers, (no city stated) 2012.
- Obituary, Lila Lee Gatlin, The Hutchinson News, November 5, 2017. Page unstated. https://www.hutchnews.com/obituaries/20170923/lila-lee-gatlin
