Measuring the Efficiency of Energy and Carbon Emissions: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Economics
Contributor:
Hongyu Diao

The International Energy Agency (IEA, 2013) believes that energy efficiency should be taken as the first fuel rather than a hidden fuel and regards it as “a key tool for boosting economic and social development. From an economic perspective, efficiency is defined as the full and most efficient use of limited and scarce resources to satisfy people’s wants and needs given the technology, that is, produce more with less. If there is no way to make someone better off and nobody worse off, then the situation is Pareto efficient. Extending this concept to production economics, a 100% Pareto–Koopmans efficiency is achieved if and only if no inputs or outputs of any decision-making unit (DMU) can be improved without worsening the other inputs or outputs. However, in most management and social science applications, the theoretically possible Pareto efficiency is unknown. Therefore, it is replaced by relative efficiency, which is fully efficient if and only if other DMUs cannot improve inputs or outputs without worsening some of its other inputs or outputs on the basis of empirically available evidence. In this case, measuring production efficiency is actually evaluating whether there is waste of input by comparing the minimum input with the actual input while the output is unchanged or evaluating whether there is an output shortage by comparing the actual output with the maximum output with the input unchanged.

  • total-factor energy efficiency
  • total-factor carbon emissions efficiency
  • carbon neutral
  • sustainable development
  • input-output variables

1. Defining Energy Efficiency and Carbon Emissions Efficiency

1.1. The Origin of Energy Efficiency and Carbon Emissions Efficiency

From an economic perspective, efficiency is defined as the full and most efficient use of limited and scarce resources to satisfy people’s wants and needs given the technology [1], that is, produce more with less. If there is no way to make someone better off and nobody worse off, then the situation is Pareto efficient [2]. Extending this concept to production economics, a 100% Pareto–Koopmans efficiency is achieved if and only if no inputs or outputs of any decision-making unit (DMU) can be improved without worsening the other inputs or outputs. However, in most management and social science applications, the theoretically possible Pareto efficiency is unknown. Therefore, it is replaced by relative efficiency [3], which is fully efficient if and only if other DMUs cannot improve inputs or outputs without worsening some of its other inputs or outputs on the basis of empirically available evidence. In this case, measuring production efficiency is actually evaluating whether there is waste of input by comparing the minimum input with the actual input while the output is unchanged or evaluating whether there is an output shortage by comparing the actual output with the maximum output with the input unchanged.

1.2. Single-Factor Indicator of Energy Efficiency and Carbon Emissions Efficiency

1.2.1. Energy Intensity

Energy efficiency was first recorded in 1888 [4] and is known as the thermal economy of a machine [5]. Patterson [6] was the first to elaborate on energy efficiency in economic terms. He defined energy efficiency as the ratio of GDP to energy consumption, commonly referred to as energy productivity. Energy intensity, as the reciprocal of energy productivity, is widely used to measure energy efficiency [7], and is used by many international organizations and countries as a strictly binding target for carbon reduction [8][9].

1.2.2. Carbon Intensity

Actual production and energy consumption will inevitably produce environmental pollution as a by-product of economic growth, of which CO2 emissions have the greatest impact on climate deterioration. Like energy intensity, carbon intensity, measured as CO2 emissions per unit of output, is also widely used as a performance indicator of carbon emissions [10][11]. Goldemberg suggested using energy intensity to analyze national trends in energy consumption and carbon intensity to analyze climate change [12][13]. With the increasing severity of climate change, in addition to energy intensity, the International Energy Agency [14] has also incorporated CO2 intensity into its statistics to assess carbon emissions and sustainability targets.

1.2.3. Inadequacy of Single-Factor Indicator

Since only a single-input factor is considered in addition to one output, energy intensity and carbon intensity are often referred to as single-factor indicators [15][16]. Although these indicators are easy to understand and convenient to measure [17][18], they do have some shortcomings. On the one hand, the measurement of intensity does not conform to the definition of efficiency in economics. Intensity has no comparison between the optimal and actual energy consumption or carbon emissions. Blindly reducing the intensity may cause economic development to deviate from the optimal state. On the other hand, intensity only focuses on the goal of realizing energy saving, carbon emissions reduction, and output growth but pays little attention to other factors, such as capital and labor and structural changes in production [19][20]. It also fails to reflect the change in technical efficiency [21]. Energy intensity may decrease due to labor substitution or organizational structure improvements rather than technological advancement in energy efficiency [22], and it reflects energy consumption rather than energy efficiency [23]. Carbon intensity separates the intrinsic connections between CO2 emissions, energy consumption, and economic growth [24][25], making it a measure of decarburization and an assessment of energy policies at a national level rather than carbon efficiency [26]. Improving energy efficiency is the most effective way to reduce the resource reallocation cost of energy saving and emission reduction.

1.3. Total-Factor Indicator of Energy Efficiency and Carbon Emissions Efficiency

Through the previous analysis, it is not difficult to find that the definition of single-factor is inconsistent with economic theory, which is divorced from reality and not in line with the production process. In view of the deficiencies of single-factor indicators, total-factor indicators are more convincing in measuring energy saving and carbon emissions reductions.
In measuring the efficiency of DMUs with multiple inputs and multiple outputs, Farrell extends the Pareto–Koopmans property to inputs and outputs, avoiding the necessity of resource prices or other weight assumptions and formal relations between inputs and outputs. This makes it possible to determine relative efficiency by taking the performance of other DMUs to evaluate the overall behavior of each DMU. The obtained result is known as Farrell efficiency [27], which can estimate the amount of input that can be saved or the amount of output that can be increased without worsening any input and output. With the assumption of equal access to inputs by all DMUs, Farrell efficiency is restricted to expressing technical efficiency. However, Farrell’s empirical work was limited to cases of a single output and failed to take into account other non-zero slack, which is an important source for mix inefficiencies in both inputs and outputs.

1.3.1. Total-Factor Energy Efficiency

On the basis of Farrell efficiency, Charnes, Cooper, and Rhodes [28] further formalized the relative efficiency, made up for the shortcomings of Farrell’s work, and developed a dual pair of linear programming model data envelopment analysis (DEA) to identify the best-practice frontier and estimate relative efficiency. The production function is generally regarded as the basis for economics. By constructing the frontier with the possibility of multiple production functions, DEA closely relates to the theory of production economics. Compared with other methods for measuring relative efficiencies, DEA does not need to set a specific function form and strict assumptions and has less data constraints [29][30]. Therefore, since the initial study of Charnes, Cooper, and Rhodes, DEA has become widely accepted and rapidly applied in a number of fields, including the nonprofit, public, and private sectors. It is often used to estimate production efficiency and to examine the overall performance of operations and management.
With more and more extensive application, in addition to deeper development of methodologies, DEA is also used to measure various efficiency values. As the catastrophic problems caused by man-made greenhouse gas emissions become more and more serious, reducing global energy consumption and CO2 emissions has attracted great interest and become a primary focus of international attention. Ramanathan [31] was the first to introduce DEA in carbon reduction and to measure the amount of carbon emissions that each country can reduce, but he did not measure specific carbon efficiency. Considering that the prominent driving factor of CO2 emissions lies in huge energy consumption, Hu and Wang [32] further proposed the concept of total-factor energy efficiency (TFEE) by employing a DEA model. This has been widely applied since it was proposed and has vigorously supporting research on energy efficiency and carbon emissions reduction.
Taking into account the role of capital, labor, and energy consumption in the production process and their contribution to GDP, TFEE is defined and measured as:
The target energy input is the minimum energy input under the best practice. Comparing the minimum energy input with the actual energy input, TFEE conforms to the definition of efficiency in economics. A higher TFEE implies less redundancy of energy and more efficiency in energy used. The difference between the actual input and the target input is the total adjustment, which is initially referred to as radial adjustment, conforming to Farrell efficiency, and later incorporates non-zero slacks to satisfy Pareto efficiency [33]. The total adjustments of energy input can be used to measure the inefficient proportion of actual energy consumption and measure the energy-saving target ratio (ESTR) [34]. The relation between TFEE and ESTR is as follows:
The higher ESTR is, the lower is TFEE, and the greater the amount of energy consumption that can be saved under the same economic growth level.

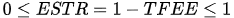
1.3.2. Total-Factor Carbon Emissions Efficiency

The scientific definition and measurement of total-factor energy efficiency is also applicable to total-factor carbon emissions efficiency. As a byproduct of economic growth generated by energy consumption, CO2 emission is generally incorporated as an undesirable output into the input-output variable [35][36]. With reference to TFEE, TFCE is calculated as follows:

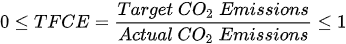
The technical efficiency measured by Charnes, Cooper, and Rhodes (1978) is the minimum efficiency value of each input and output, reflecting the overall performance of each DMU relative to inputs and outputs, so it is usually used to measure environmental or ecological efficiency [37][38]. Compared with overall efficiency, TFEE and TFCE only indicate the performance of energy saving and CO2 emissions, so they are more convincing in the measurement of specific sustainable development goals. In addition, on the basis of TFEE and TFCE, some new indicators for measuring energy consumption and carbon emissions have been developed, such as energy performance index, defined as the ratio of actual energy efficiency to target energy efficiency, and carbon performance index, measured as the ratio of target carbon intensity to actual carbon intensity [30][39].

2. Efficiency Measurement Model Based on DEA

The concept and idea of data envelopment analysis (DEA) was first proposed by Farrell [27] and is a commonly used benchmark tool to measure the production efficiency of decision-making units (DMUs) and to reflect their performance. DEA is a method that is easy to operate. It does not need to make any restrictive assumptions about relevant functions and can deal with multiple input and output variables of different units.

2.1. Radial Model

2.1.1. CCR

In 1978, Charnes, Cooper, and Rhode [28] first proposed an input-oriented data envelopment analysis, which is based on Constant Return to Scale (CRS) in the intersection of mathematics, operational research, mathematical economics, and management science. Subsequently, this method has attracted widespread attention and application. An input-oriented CRS-DEA model can be expounded as follows:

In the case of the production, technology was defined as T = x , q : q ≤ Q λ ,   x ≥ X λ . Suppose that there are I DMUs, and each DMU has N inputs and M outputs. Measuring the efficiency of the ith DMU is to solve the following mathematical programming problem:

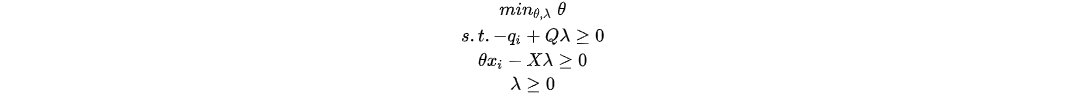
where θ is a scalar, and λ is a I × 1 vector of constants. The column vectors x i and q i represent the ith DMU’s input and output, respectively. The N × I input matrix X and the M × I output matrix Q represent the data for all I DMUs. The value of θ is the efficiency score for the ith DMU. The DMU with a score = 1 is the efficient DMU, which means the DMU is on the frontier.

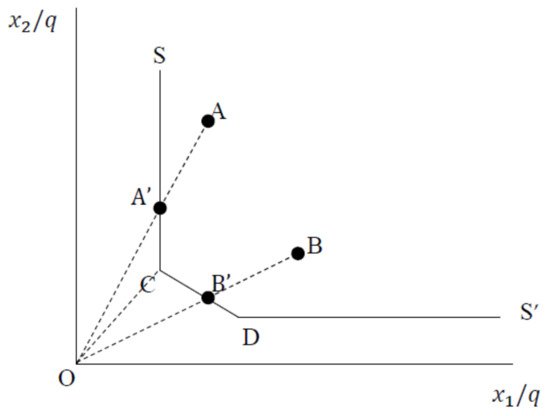
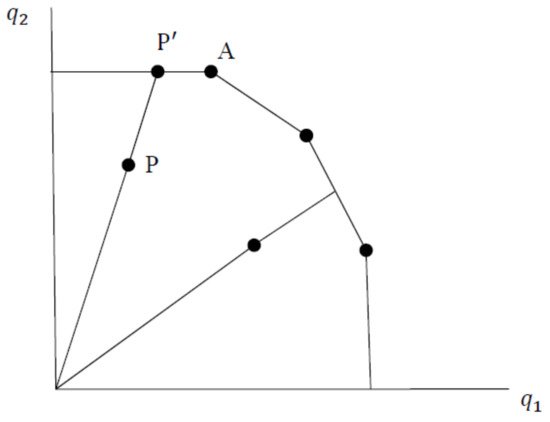
According to Figure 1, SS’ is a piece-wise linear isoquant determined by all the DMUs in the sample, where the radial contraction of the input vector is ( X λ ,   Q λ ) , the radial adjustment is AA’, and the constraints in Equation (1) ensure that the projected point cannot lie outside the feasible set. There are four firms, A, B, C, and D, where firms using input combinations C and D are the two efficient firms that define the frontier, and firms A and B are inefficient firms. Based on the measure of technical efficiency, the efficiency of A and B can be represented as OA′/OA and OB′/OB, respectively. However, it is not certain if A′ is an efficient point because when the use of input x 2 is reduced (that is, CA’), it still produces the same output. For firm B, it is effective when B moves to B′, as its input combinations change, i.e., efficiency equals one.

Energies 15 00962 g006 550
Figure 1. Input-oriented CRS-DEA model.

2.1.2. BCC

Considering that in the case of imperfect competition, government regulation, financial constraints, etc., the CRS assumptions will no longer pertain, Banker, Charnes, and Cooper [40] proposed to improve the CRS-DEA method by adding convexity constraint I 1 ′ λ = 1 into the CRS-DEA model to explain Variable Return to Scale (VRS).

In order to explain VRS, the CRS linear programming problem can be easily modified by adding the convexity constraint to Equation (2):
where I 1 is the I × 1 vector with element 1. This approach forms a convex hull of intersecting planes that more closely encloses data points than the conical hull of CRS. Therefore, the measured technical efficiency value is greater than or equal to that obtained by the CRS model.
Similar to Figure 1, in Figure 2, an output-orientated DEA with two outputs could also be represented by a piece-wise linear production possibility curve. When point P is projected to the point P′, it is on the frontier but not on the efficient frontier because the production of q i could be increased by the amount AP’ without using any more inputs.
Energies 15 00962 g007 550
Figure 2. Output-oriented VRS-DEA model.

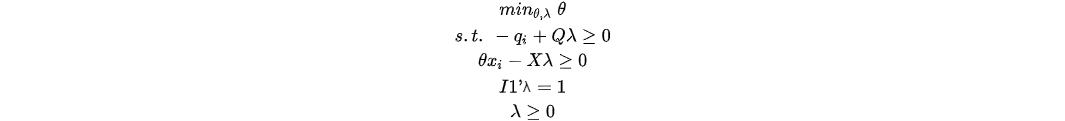
2.2. Non-Radial Model

2.2.1. Traditional Slacks-Based Measure (SBM) Model

In the traditional CRS/VRS-DEA model, the inefficient decision-making unit achieves the effective state by reducing all inputs or expanding all outputs in the same proportion. Therefore, the traditional DEA model is also referred to as a radial model. When the DMU is inefficient, there is a certain distance between the current state and the optimal target. In the radial model, this distance is equal to the sum of the radial improvement and the slack improvement, but the latter is not reflected in the efficiency measurement of the radial model.
In this context, Tone (2001) [41] proposed a non-radial and non-angular Slacks-Based Measure model, which directly introduced the slack variable into the objective function. The SBM model can find the target energy input more effectively, avoid the influence and error caused by radial and angle differences, better reflect the essence of efficiency measurement, and improve the reliability and accuracy of efficiency measurement.

2.2.2. Slacks-Based Measure (SBM) Model with Undesirable Output

Tone (2004) [42] constructed the SBM model by taking undesirable outputs into account. Therefore, compared with other DEA models, the SBM model with undesirable output can better reflect the essence of efficiency evaluation.
Suppose that there are n DMUs, and each D M U j j = 1 , 2 , … , n has m inputs x j = x 1 j , x 2 j , … , x m j ’ , s 1 desirable outputs y j g = y 1 j g , y 2 j g , … , y s 1 j g ’ , and s 2 undesirable outputs y j b = y 1 j b , y 2 j b , … , y s 2 j b ’ . The production possibility set was defined as P = { x , y g , y b | x ≥ X λ , y g ≤ Y g λ , y b ≥ Y b λ , λ ≥ 0 } . The specific model is expressed as follows:

where s − ∈ R m , s b ∈ R s 2 , and s g ∈ R s 1 are all slacks. 0 < ρ ≤ 1 , when ρ = 1 means the DMU is on the production frontier, which is completely efficient.

3. Input-Output Variables for Efficiency Measurement

The seemingly straightforward measurements have their underlying theoretical and empirical assumptions [43]. Efficiency can be defined and measured in various forms, and the results obtained can affect socio-economic development in different ways, such as placing an unfair burden of carbon reduction on consumers and isolating humans from the natural world. In efficiency measurement, social scientists call for more observation of complex social contexts and practices and the dissecting of efficiency from conceptual foundations, practical applications, and sociology [44][45][46]. This is mainly reflected in the selection of input and output variables of efficiency measurement.

3.1. Production Possibility Set

According to production economics [47][48], DMU must ensure the technological feasibility in the production process of transforming inputs into outputs. The state of technology determines and restricts the possibility of inputs to produce outputs. The most general way to express this constraint is to think of the DMU as having a production possibility set, Y ⊂ R n , where each vector y = y 1 , … , y n ∈ Y is a technologically feasible production plan, observing the convention of y j < 0 if resource j is consumed as input, and y j > 0 if it is produced as an output. In this way, the set Y can fully describe the technological possibilities facing the DMU.

In DEA, production technology set Y is set to describe a multi-input and multi-output production technology [49]. Assuming that x and q denote a non-negative N × 1 input vector and a non-negative M × 1 output vector, respectively, the set S is then defined as:

Consisting of all input-output vectors x , q , the set S can be equivalently defined using the output set P x of all output vectors q that can be produced by the input vector x or the input set L q of all input vectors x that can produce a given output vector q [50]. In addition, P x is also the basis for describing the production possibility curve of two-dimensional output vectors and is sometimes referred to as the production possibility set related to various input vectors x.

3.2. Input-Output Variables Selection

As an improvement of single-factor energy efficiency, total-factor energy efficiency overcomes the one-sidedness of single-factor energy efficiency to a certain extent and takes into account the coordination and substitution of factors. However, in the existing literature, the selected input-output variables are repeated or omitted, and this does not conform to the theory of production economics and the actual production situation.
In the current research on TFEE, the most commonly selected variables are capital, labor, and energy as input variables and value added as output variable [15][19][51]. Some scholars also chose the value of output as an output variable [52]. On this basis, some scholars consider the impact of the environment and add undesirable outputs into the output variable [53]. Some scholars have also considered other intermediate inputs [54]. However, these studies have a certain degree of repetition or omission in the selection of variables.
The input-output variables of total-factor energy efficiency (TFEE) are also applicable to the measurement of total-factor carbon emissions efficiency (TFCE). Pang (2015) chose employment, capital stock, and energy use as inputs; GDP as desirable output; and CO2 emissions as undesirable output, analyzing the impact of clean energy utilization on TFEE and TFCE, respectively. Based on the measurement of TFEE, Li and Lin (2017) also added CO2 emissions as an undesirable output and measured the TFCE.
Based on a comprehensive review of previous studies, this paper indicates an improved measurement method for total-factor efficiency and proposes a more accurate and complete measurement input-output variables of energy efficiency, which provides a scientific method for measuring energy efficiency and carbon emissions efficiency. In order to ensure the accuracy and reliability of results for energy efficiency measurement, it is necessary to select the most appropriate input-output variables. Input-output variables must be consistent with and reflect the production process as close to reality as possible.

This entry is adapted from the peer-reviewed paper 10.3390/en15030962

References

  1. Samuelson, P.A.; Nordhaus, W.D. Economics, 19th ed.; McGraw-Hill: New York, NY, USA, 2010.
  2. Jehle, G.A.; Reny, P.J. Advanced Microeconomic Theory, 3rd ed.; Prentice Hall: Harlow, UK, 2011.
  3. Cooper, W.W.; Seiford, L.M.; Zhu, J. Handbook on Data Envelopment Analysis; Kluwer Academic Publishers: Boston, MA, USA, 2004.
  4. Dunlop, T. Mind the gap: A social sciences review of energy efficiency. Energy Res. Soc. Sci. 2019, 56, 101216.
  5. Alexander, J.K. The Mantra of Efficiency: From Waterwheel to Social Control; The Johns Hopkins University Press: Baltimore, MD, USA, 2008.
  6. Patterson, M.G. What is energy efficiency?: Concepts, indicators and methodological issues. Energy Policy 1996, 24, 377–390.
  7. Cheng, M.; Yang, S.; Wen, Z. The effect of technological factors on industrial energy intensity in China: New evidence from the technological diversification. Sustain. Prod. Consum. 2021, 28, 775–785.
  8. IEA. Energy Efficiency. 2020. Available online: https://www.iea.org/reports/energy-efficiency-2020 (accessed on 14 September 2021).
  9. United Nations (UN). Sustainable Development Goals 7: Affordable and Clean Energy. Available online: https://www.un.org/sustainabledevelopment/energy/ (accessed on 14 September 2021).
  10. Su, B.; Ang, B.W. Demand contributors and driving factors of Singapore’s aggregate carbon intensities. Energy Policy 2020, 146, 111817.
  11. He, W.; Zhang, B.; Ding, T. Sources of provincial carbon intensity reduction potential in China: A non-parametric fractional programming approach. Sci. Total Environ. 2020, 730, 139037.
  12. Goldemberg, J. A note on the energy intensity of developing countries. Energy Policy 1996, 24, 759–761.
  13. Mielnik, O.; Goldemberg, J. The evolution of the carbonization index in developing countries. Energy Policy 1999, 27, 307–308.
  14. IEA. Data and Statistics. Available online: https://www.iea.org/data-and-statistics/data-browser/?country=WORLD&fuel=CO2%20emissions&indicator=CO2BySource (accessed on 14 September 2021).
  15. Borozan, D. Technical and total factor energy efficiency of European regions: A two-stage approach. Energy 2018, 152, 521–532.
  16. Wu, H.; Hao, Y.; Ren, S. How do environmental regulation and environmental decentralization affect green total factor energy efficiency: Evidence from China. Energy Econ. 2020, 91, 104880.
  17. Shi, G.-M.; Bi, J.; Wang, J.-N. Chinese regional industrial energy efficiency evaluation based on a DEA model of fixing non-energy inputs. Energy Policy 2010, 38, 6172–6179.
  18. Cheng, Z.; Li, L.; Liu, J. Industrial structure, technical progress and carbon intensity in China’s provinces. Renew. Sustain. Energy Rev. 2018, 81, 2935–2946.
  19. Huo, T.; Tang, M.; Cai, W.; Ren, H.; Liu, B.; Hu, X. Provincial total-factor energy efficiency considering floor space under construction: An empirical analysis of China’s construction industry. J. Clean. Prod. 2020, 244, 118749.
  20. Cheng, Z.; Liu, J.; Li, L.; Gu, X. Research on meta-frontier total-factor energy efficiency and its spatial convergence in Chinese provinces. Energy Econ. 2020, 86, 104702.
  21. Liu, H.; Zhang, Z.; Zhang, T.; Wang, L. Revisiting China’s provincial energy efficiency and its influencing factors. Energy 2020, 208, 118361.
  22. Renshaw, E.F. Energy efficiency and the slump in labour productivity in the USA. Energy Econ. 1981, 3, 36–42.
  23. Proskuryakova, L.; Kovalev, A. Measuring energy efficiency: Is energy intensity a good evidence base? Appl. Energy 2015, 138, 450–459.
  24. Yao, X.; Guo, C.; Shao, S.; Jiang, Z. Total-factor CO2 emission performance of China’s provincial industrial sector: A meta-frontier non-radial Malmquist index approach. Appl. Energy 2016, 184, 1142–1153.
  25. Trinks, A.; Mulder, M.; Scholtens, B. An Efficiency Perspective on Carbon Emissions and Financial Performance. Ecol. Econ. 2020, 175, 106632.
  26. Sun, J.W. The decrease of CO2 emission intensity is decarbonization at national and global levels. Energy Policy 2005, 33, 975–978.
  27. Farrell, M.J. The measurement of productive efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253–290.
  28. Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444.
  29. Wang, Q.; Su, B.; Sun, J.; Zhou, P.; Zhou, D. Measurement and decomposition of energy-saving and emissions reduction performance in Chinese cities. Appl. Energy 2015, 151, 85–92.
  30. Cheng, Z.; Li, L.; Liu, J.; Zhang, H. Total-factor carbon emission efficiency of China’s provincial industrial sector and its dynamic evolution. Renew. Sustain. Energy Rev. 2018, 94, 330–339.
  31. Ramanathan, R. Combining indicators of energy consumption and CO2 emissions-a cross-country comparison. Int. J. Glob. Energy Issues 2002, 17, 214–227.
  32. Hu, J.-L.; Wang, S.-C. Total-factor energy efficiency of regions in China. Energy Policy 2006, 34, 3206–3217.
  33. Ferrier, G.D.; Lovell, C.K.X. Measuring cost efficiency in banking Econometric and linear programming evidence. J. Econom. 1990, 46, 229–245.
  34. Honma, S.; Hu, J.-L. Total-factor energy efficiency of regions in Japan. Energy Policy 2008, 36, 821–833.
  35. Apergis, N.; Aye, G.C.; Barros, C.P.; Gupta, R.; Wanke, P. Energy efficiency of selected OECD countries: A slacks based model with undesirable outputs. Energy Econ. 2015, 51, 45–53.
  36. Deng, X.; Du, L. Estimating the environmental efficiency, productivity, and shadow price of carbon dioxide emissions for the Belt and Road Initiative countries. J. Clean. Prod. 2020, 277, 123808.
  37. Zhang, J.; Zeng, W.; Shi, H. Regional environmental efficiency in China: Analysis based on a regional slack-based measure with environmental undesirable outputs. Ecol. Indic. 2016, 71, 218–228.
  38. Wu, J.; Li, M.; Zhu, Q.; Zhou, Z.; Liang, L. Energy and environmental efficiency measurement of China’s industrial sectors: A DEA model with non-homogeneous inputs and outputs. Energy Econ. 2019, 78, 468–480.
  39. Zhou, P.; Ang, B.W.; Wang, H. Energy and CO2 emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. Oper. Res. 2012, 221, 625–635.
  40. Banker, R.D.; Charnes, A.; Cooper, W.W.; Swarts, J.; Thomas, D.A. An introduction to data envelopment analysis with some of its models and their uses. Res. Gov. Nonprofit Account. 1989, 5, 125–165.
  41. Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509.
  42. Tone, K. Dealing with Undesirable Outputs in DEA: A Slacks-based Measure (SBM) Approach Spring 2004 Research Presentation. 2004. Available online: https://www.researchgate.net/publication/284047010 (accessed on 27 September 2021).
  43. Campbell, N.R. Physics the Elements; Cambridge University Press: London, UK, 2013.
  44. Lutzenhiser, L. Through the energy efficiency looking glass. Energy Res. Soc. Sci. 2014, 1, 141–151.
  45. Herring, H. Is energy efficiency good for the environment? Some conflicts and confusions. In The UK Energy Experience: A Model or A Warning? World Scientific Publishing Co. Pte. Ltd.: Singapore, 1996; pp. 327–338.
  46. Shove, E. What is wrong with energy efficiency? Building Res. Inf. 2017, 46, 779–789.
  47. Varian, H.R. Microeconomic Analysis, 3rd ed.; W. W. Norton & Company: New York, NY, USA, 1992.
  48. Mas-Colell, A.; Whinston, M.D.; Green, J.R. Microeconomic Theory; Oxford University Press: New York, NY, USA, 1995.
  49. Färe, R.; Primont, D. Multi-Output Production and Duality: Theory and Applications; Kluwer Academic Publishers: Boston, MA, USA, 1995.
  50. Coelli, T.J.; Prasada Rao, D.S.; O’Donnell, C.J.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer Science and Business Media, Inc: New York, NY, USA, 2005.
  51. Tang, L.; He, G. How to improve total factor energy efficiency? An empirical analysis of the Yangtze River economic belt of China. Energy 2021, 235, 121375.
  52. Ali, A.; Mohsen, A.; Ghaderi, S.F.; Asadzadeh, S.M. Corrigendum to An integrated DEA PCA numerical taxonomy approach for energy efficiency assessment and consumption optimization in energy intensive manufacturing sectors? Energy Policy 2008, 35, 3792–3806.
  53. Wang, H.; Wang, M. Effects of technological innovation on energy efficiency in China: Evidence from dynamic panel of 284 cities. Sci. Total Environ. 2020, 709, 136172.
  54. Honma, S.; Hu, J.-L. Industry-level total-factor energy efficiency in developed countries: A Japan-centered analysis. Appl. Energy 2014, 119, 67–78.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback