Methods for Imaging and Evaluation of Scoliosis: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Computer Science, Artificial Intelligence | Medical Informatics
Contributor:
Daniel Feige

Scoliosis is defined as a three-dimensional spinal deformity consisting of a lateral curvature greater than 10 degrees with rotation of the vertebrae within the curve. It can be identified as congenital, neuromuscular or idiopathic. Idiopathic scoliosis (IS) can be further classified by age of onset: infantile (birth to two years), juvenile (three to nine years), and adolescent (10 years and older). It is the most common pediatric musculoskeletal disorder that causes a three-dimensional (3D) spinal deformity. The deformity is always 3D because it also involves an axial rotation of the vertebrae, not just displacement and rotation in the frontal plane. Adolescent IS is the most common form because the spinal deformity evolves during periods of significant physical growth. IS is diagnosed when other etiological factors cannot be identified, such as congenital neurological or musculoskeletal anomalies, or inflammatory or demyelinating processes leading to primary or secondary motor neuron damage (myotonia, myopathy, etc.).

  • spine
  • diagnostic imaging
  • computer analysis
  • artificial intelligence diagnosis
  • scoliosis
  • spinal curvatures

1. Methods for Imaging and Evaluation of Scoliosis Using Radiography

Radiography, commonly called X-ray [1], is very important in imaging the spine. It provides a basic image, giving a general picture of the possible two projections (anterior-posterior (AP)/posterior-anterior (PA) and lateral (LAT)). At one time, X-rays of the spine were very commonly performed, but over time, efforts have been made to limit patient exposure to X-rays. Between 1935 and 1965, the incidence of breast cancer was almost doubled [2]. Today, radiation doses are lower, but the number of x-rays that must be taken of children during adolescence after/or during diagnosis is at least 12. Unfortunately, the risk of cancer due to cumulative X-ray dose is several times higher in children than in adults [3][4][5].
The development of technology and computerization allowed for the use of optoelectronic methods to localize the problem of posture and body statics. Unfortunately, the irreplaceable advantage of X-rays so far is the possibility of calculating the angle of torsion using the Cobb method and observing morphological changes in the vertebrae. As previously mentioned, an X-ray is an examination that carries harmful radiation, which means that the diagnosis is usually stretched over time. Medical personnel are not able to precisely determine whether the applied treatment process proceeds properly or whether it brings the desired results. Therefore, the ideal diagnostic tool is computer diagnostic methods; they are precise and non-invasive without the harmful effects of X-rays. Computer methods testing the posture are of practical importance because they allow us to catch the first signs of curvature. Additionally, they allow us to observe the patient’s body in all planes and to localize the problem, which may not yet be visible to the naked eye. Computerized methods of posture examination include the Moiré bar method, ISIS method, Posturomet-S, Metrecom System method and Diers formetric III 4D optoelectronic method [6][7][8][9][10][11][12][13].

2. Method for Imaging and Evaluation of Scoliosis Using Magnetic Resonance Imaging (MRI)

Magnetic resonance imaging (MRI) is a non-invasive method that is finding more and more applications, mainly in the development of specialized methods and sequences. The test uses a hydrogen atom, which makes the magnetic resonance process possible because it has a spin and a magnetic moment. The individual magnetic moments returned are disordered, but when a strong external magnetic field (B0) is applied, the magnetic moment returns are ordered—vectors parallel or anti-parallel to the main magnetic field. Atoms with an odd number of protons and/or neutrons can be visualized as spinning charged spheres with a small magnetic moment. An MR scanner has three magnetic fields that interact with these spinning spheres, commonly called spins, namely, the main magnetic field (B0), the radio frequency (RF) field (B1) and the gradient field (G). Under the external influence of a magnetic B0, some of the spins are aligned with it and hence have a net nonzero magnetic moment.
Following excitation by an RF pulse (B1), the net magnetization vector is tipped into the transverse plane, where it rotates about the external field at the Larmor frequency, giving rise to the MR signal. A second action of the RF pulse causes the spins to become aligned in orientation or to become phase coherent in the transverse plane. Over time, it recovers back to equilibrium, with the individual spins returning to their parallel or anti-parallel orientations and losing their phase coherence. As a result, it reforms along the z-axis, parallel with the applied main magnetic field, and with a magnitude of M0. This return to equilibrium is characterized by two orthogonal processes: longitudinal (T1) and transverse (T2) relaxation, governed by the T1 and T2 relaxation time constants. T1 relaxation describes the recovery along the longitudinal (z) direction (with the T1 being the time corresponding to the recovery of 63% of the equilibrium value), whilst T2 characterizes the loss of phase coherence in the transverse plane (with the T2 time corresponding to the loss of 63% of the initial value).
This signal is detected by specially designed RF coils and sent to a computer for image reconstruction. The times at which the excited atoms of the tissues under study return to equilibrium, or relaxation times, are represented by different shades of grey in the image [14].
This phenomenon is possible because hydrogen is part of the water molecule, which makes up 60–70% of the human body. Additionally, hydrogen is located in fat. The way hydrogen is distributed in different parts of the body is a parameter that differentiates different structures. Both the relaxation times and the density of protons affect the brightness, which is the degree of grey obtained in an image. The examination is associated with a strong magnetic field; for this reason, it is not recommended for patients with metal implants. The health risks resulting from the examination are very small, usually associated with the occurrence of allergic reactions immediately after the administration of the contrast medium.
The second stage involves detecting the MR signal and reconstructing it to create an image and is termed ‘acquisition’. Spatial encoding of the MR signal requires localization in three dimensions. In single-slice Cartesian 2D imaging, one first excites the nuclear spins in a thin slice, then plays a phase-encoding gradient pulse to impose a definite phase relationship across an in-slice direction, and finally reads out the signal, while a linear magnetic field gradient is played in the perpendicular in-slice direction (frequency encoding). This sequence of RF and gradient pulses is repeated for each phase encoding gradient, and finally, a 2D Fourier transform of the acquired signal reconstructs the image [15].
Most of the modern diagnostic methods today are widely used in many specialty fields. The fields of physics, computer science and medicine can be said to have been combined. MRI can be performed on virtually any part of the body using an appropriately selected sequence.
On the one hand, society is demanding greater accessibility for diagnostic support, particularly related to MRI access and scoliosis assessment. MRI is used in the diagnosis of patients with scoliosis primarily to evaluate neural structures and the shape of the spinal canal. Of note, this examination should not be repeated more than once. The routine, preoperative use of MRI remains controversial and current indications for MRI in idiopathic scoliosis vary from study to study (e.g., early scoliosis) [16]. The literature suggests and even excludes the use of MRI in specific cases such as routine preoperative MRI in idiopathic scoliosis unless the patient has neurological deficits [17][18]. MRI are used in the suspicion of congenital bone defects of the spine, e.g., Klippel-Feil syndrome, underdevelopment of the vertebrae, semivertebrae, intermolar adhesions, adhesions of articular processes, rib adhesions and bone blocks. Nerve bone defects, e.g., meningeal hernia (myelocele, myelomeningocele), were also observed. In addition, in the diagnosis of the nervous system, e.g., Recklinghausen’s disease, spinal tumors, syringomyelia, Arnold Charie’s syndrome. MRI is also indicated for scoliosis with an atypical pattern (for example, left thoracic scoliosis), in the diagnosis of congenital curvature of the spine and for concomitant neurologic disorders to detect nervous system defects [19]. Scoliosis also causes a number of dysfunctions in a person who is sick. In addition, diseases emerge from the formation of scoliosis, such as syringomyelia [20], vertebral segmentation anomaly, intramedullary spinal tumor [21] or Chiari malformation [22].
Magnetic resonance imaging may be beneficial for patients with presumed idiopathic scoliosis, and its non-invasiveness and precision contribute to improved diagnosis in the youngest patients without unnecessary exposure to X-rays.
Measurement methods have evolved sequentially since about 2002, where Rogers et al. [23] presented a method based on measuring intervertebral rotation in the lumbar spine. The method has found application in both MRI and CT [24].
Unfortunately, because MRI scans are expensive, they have been limited to studies of patients with congenital and severe curvatures [25]. Medicine of the 21st century is more and more personalized, where we observe the development of dedicated implants. A dedicated implant is a solution that is more and more often used in spine surgery when it is necessary to recreate the correct curvature of the spine, which has been lost as a result of degenerative disease, or as a result of a congenital defect or a complicated disorder of the spine axis. Such a spine is unable to maintain a proper line and tilts to the side or rotates or slides forward.
Materials from which the implants are made include polyetheretherketone (PEEK), titanium [26], cobalt-chromium [27], or other materials, e.g., bio-absorbable materials. The former is transparent to X-rays; therefore, these implants contain small radiographic markers. Titanium implants, on the other hand, are visible on radiographs and safe in MR imaging [28].

3. Computed Tomography (CT)

Although 2D images are still widely used in clinical research, advances in medicine have led to the development of a new 3D technique, which has become an important modern tool, obtained using computed tomography (CT) [29][30] and magnetic resonance imaging (MRI). These methods are certainly being developed at a very fast pace, and these methods are completely automated or semi-automated (requiring little intervention). Computed tomography was quickly appreciated because of the difficulty of evaluating X-ray images, which were usually taken in two projections. However, this did not give a complete picture of the problem, and curvature assessment was not problematic.
Computed tomography has been successfully used to take cross-sectional images of the body parts examined since 1973 (introducing tomographs to hospitals).
The 20th and 21st centuries tightened the procedures related to the use of X-rays, introducing even more restrictions related to the application of radiological protection to the patient. Due to the desire to limit radiation exposure, cross-sections are usually made at the level of the border vertebrae, the vertebral column, and the pelvis [31]. With the ever-increasing number of medical images, more and more methods that are fully automated or semi-automated, i.e., requiring minimal manual intervention, have appeared; however, they apply mainly to digital radiography X-rays. In contrast, in CT examinations, the clinician must set adequate parameters to better check the disease or the degree of scoliosis. The parameters should be optimized, and they require very good knowledge of the influence of parameters on the results. Thus, using specially developed methods for quantitative assessment of spinal curvatures that can improve medical diagnosis, treatment, and management of spinal disorders is necessary and will support the work of doctors.
Enhancing the CT method with three-dimensional image processing is possible. This allows for spatial imaging of the spine, the detection of spinal canal deformities, the detection of congenital malformations of the spine, the visualization of the location of spinal implants, and the assessment of the quality of spondylodesis. This examination plays an important role in the choice of surgical technique.

4. Artificial Intelligence (AI) As a Method for Detection of Scoliosis

Theories of artificial intelligence: neural networks mirror the behavior of the human brain, enabling computer programs to recognize patterns and to solve common problems in the fields of artificial intelligence, machine learning and deep learning.
Neural networks, also known as artificial neural networks (ANNs) or simulated neural networks (SNNs), are part of the machine learning function and form the basis of deep learning algorithms.
Artificial neural networks (ANNs) are composed of node layers that include an input layer, one or more hidden layers and an output layer. Each node (artificial neuron) connects to another and has an associated weight and threshold. If the output of a single node exceeds a certain threshold, that node is activated when sending data to the next network layer. Otherwise, no data are passed on to the next layer of the network.
How do neural networks work? Think of each individual node as a linear regression model composed of inputs, weights, variations (or thresholds) and outputs. The formula is thus as follows:
∑ i = 1 m w i x i   + b i a s = w 1 x 1 + w 2 x 2   + w 3 x 3   + b i a s O u t p u t = f ( x ) = { 1   i f   ∑ w 1 x 1 + b ≥ 0 0   i f   ∑ w 1 x 1 + b < 0
General formula describing the operation of a neuron:
y =   f ( s )
where in:
S = ∑ i = o n x i w i
The activation function may take various forms depending on the specific model neuron. After determining the input layer, weights are assigned. Neural networks can be classified into different types and used for different purposes. The following list is not exhaustive; however, it is representative and presents the most common types of neural networks, with the oldest neural network being the perceptron, created by Frank Rosenblatt in 1958, with one neuron, and is the simplest form of neural network.
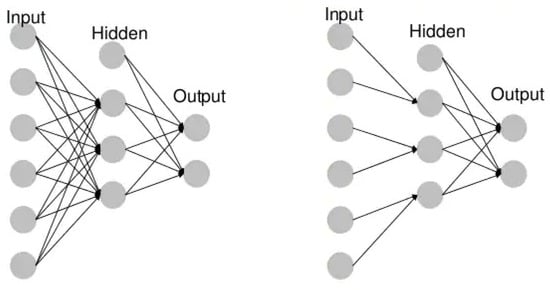
  • Unidirectional neural networks, i.e., multilayer perceptrons (MLP) (Figure 1), consist of an input layer, a hidden layer(s) and an output layer. While these neural networks are also commonly referred to as MLPs, keep in mind that they are actually sigmoidal neurons, not perceptrons, as most real-world problems are non-linear. Data are used to train these models. They form the basis of computer vision, natural language processing and other neural networks.
  • Convolutional neural networks (CNNs) are similar to unidirectional networks but are typically used for image recognition, pattern recognition and/or computer vision. These networks use the principles of linear algebra, in particular, matrix multiplication, to identify patterns in an image.
  • Recursive neural networks (RNNs) are distinguished based on feedback loops.

4.1. Neural Networks and Deep Learning

The terms “deep learning” and “neural networks” are often used interchangeably, which can be confusing. The word “deep” in “deep learning” only refers to layer depth in a neural network. A neural network that consists of more than three layers-including inputs and outputs-can be considered a deep learning algorithm. A neural network that has only two or three layers is just a basic neural network. The structure and use of deep nets has already been described in detail, which translates into the number of publications in the PubMed database. One of the newer publications, which is an interesting and modern comparison in the context of the discussed scoliosis, was presented by Chen et al. [32].
Between 2019 and 2021, the interest in artificial intelligence and methods such as deep learning and machine learning has seen an unimaginable increase; for example, they have begun to be used in the fight against COVID-19. The development of deep learning algorithms and methods also contribute to the development of other imaging methods and, consequently, diagnostics not directly related to COVID-19.
Traditional scoliosis screening methods are readily available but require referrals and radiographic exposures due to their low positive predictive value. The use of deep learning algorithms has the potential to reduce unnecessary referrals and, for example, scoliosis screening costs.
Publications directly related to the application of AI in scoliosis diagnosis that has appeared within two years are few thus far. The topic is evolving rapidly; however, the techniques are not yet used in standard diagnostics.
Yang et al. [33] presented an algorithm to identify cases with a curvature ≥ 20° and performed degree classification using uncovered back images with accuracy, sensitivity, specificity and positive predictive values (PPV) that are higher or comparable with those obtained by human experts. The use of algorithms can reduce the number of referrals, costs and time required for traditional scoliosis screening. Additionally, because deep learning algorithms (DLA) do not require radiation exposure, the method can be used as a periodic tool to monitor disease progression, thus avoiding excessive X-ray exposure. To our knowledge, this is the first large and complete study (including healthy control groups and different degrees of curvature) on intelligent scoliosis detection. The effectiveness of computer vision in scoliosis detection and classification has been demonstrated using uncovered back images.
Machine learning methods have already been used to detect spinal deformities using the torso surface defined by various techniques, including optical digitizing systems [34][35], orthogonal maps, surface topography techniques [36], laser scanners [37][38] and the Quantec system [39]. However, these methods still cannot be widely used due to the small scoliosis datasets, a lack of healthy control groups, the need for specialized equipment and the time-consuming nature of these methods. According to the authors, the above-mentioned methods, excluding X-rays, are perfectly sufficient. Limiting X-ray images is absolutely advisable and justified when specialists have alternative visualization methods.

4.2. Automatic Measurement Algorithm of Scoliosis Cobb Angle Based on Deep Learning

Zhang et al. [40] proposed a computer-aided Cobb angle measurement method based on Hough transform, which can automatically calculate the Cobb angle after manually selecting the region of interest (ROI) of the end circles and adjusting the brightness and contrast of the X-ray images. The Hough transform is based on the detection of regular shapes in computer vision. It is a special case of Radon transform known since 1917. The subject has developed relatively rapidly. In the paper by Samuvela et al. [41], an algorithm was presented to measure the Cobb angle. The algorithm was based on segmentation by applying a so-called mask. In another paper, Zhang [42] proposed an algorithm based on a deep neural network that can automatically estimate the slope of the spine after manually selecting the block of interest in the upper and lower vertebrae and can automatically measure the Cobb angle. Moreover, programs were also designed to measure the angle and improve the efficiency of radiologists [43][44]. As it turned out, the programs improved the efficiency of angle measurement; however, the upper and lower extremities of the vertebra had to be selected manually, which was time-consuming and subjective. This problem caused the development of more precise and stable methods. Image processing algorithms were improved, e.g., machine learning target detection algorithms [45] and algorithms for automatic image segmentation [46]. Thus, over several years, the methods have improved. The methods described above are related to the subjective experience of the clinician and contributed to the high measurement error of Cobb angles on scoliosis X-rays. Yongcheng et al. [47] proposed an automatic algorithm based on deep learning [48]. For spinal contour segmentation, they proposed DU-Net detection and segmentation network on spinal X-rays. The aggregated channel features in the detection algorithm are fed into the scoliosis image to detect the spine region. DU-Net is trained to segment the spinal contours. Therefore, the spine curve can be fitted to the spine contour, and the Cobb angle can be automatically measured using the tangent line of the spine curve. As a result, the Cobb angle automatic measurement method yields an average error of 2.9° compared with the orthopedist’s manual measurement.
Earlier methods of scoliosis evaluation based on segmentation consisting of filtering [40][49], active contouring [50] and physical models [51] localize the required vertebrae and calculate Cobb’s angle. These methods require the user to select circles, which is a limitation of these methods. As of 2021, no benchmarks, procedures or workflows have emerged to standardize the analysis performed and the selection of methods and algorithms.
In recent years, direct estimation methods [52][53][54], which aim to obtain relationships between medical images and clinical measurements directly without segmentation-based results, have achieved great success; they have been applied to measure scoliosis [52][53][54]. Unfortunately, these methods account for the basic relationship between AP and LAT X-rays but do not account for the unique features of AP and LAT projection images. Due to these limitations, Wang et al. [55] proposed an automated Cobb angle estimation method for scoliosis assessment using MVE-Net. They presented that MVE-Net effectively utilizes joint features and independent features in X-ray images from multiple perspectives. MVE-Net achieved high precision in Cobb angle estimation on both AP and LAT images in a large dataset of 526 X-ray images with different degrees of scoliosis. The computational method is also extendable to other clinical applications for high precision estimation.
Deep learning algorithms (DLAs) from CNNs, which have been applied to the detection of idiopathic scoliosis, were developed using 2D images [33] or Moiré topography [56][57][58]. Kokabu et al. [59] modified their system [60] to predict the Cobb angle even more accurately, which they successfully presented in their current publication.
Sensors 21 08410 g003 550
Figure 1. Example MLP vs. CNN.

This entry is adapted from the peer-reviewed paper 10.3390/s21248410

References

  1. Kalender, W.A. X-ray Computed Tomography. Phys. Med. Biol. 2006, 51, R29–R43.
  2. Hoffman, D.A.; Lonstein, J.E.; Morin, M.M.; Visscher, W.; Harris, B.S.; Boice, J.D. Breast Cancer in Women with Scoliosis Exposed to Multiple Diagnostic x Rays. J. Natl. Cancer Inst. 1989, 81, 1307–1312.
  3. Kutanzi, K.; Lumen, A.; Koturbash, I.; Miousse, I. Pediatric Exposures to Ionizing Radiation: Carcinogenic Considerations. Int. J. Environ. Res. Public Health 2016, 13, 1057.
  4. IARC Monographs on the Evaluation of Carcionogenic Risks to Humans. Available online: https://monographs.iarc.who.int/wp-content/uploads/2018/08/14-002.pdf (accessed on 1 December 2021).
  5. UNSCEAR 2013 Report to the General Assembly with Scientific Annexes Volume II: Scientific Annex B. 283. Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/UNSCEAR_2013_Report_Annex_B_Children.pdf (accessed on 1 December 2021).
  6. Harzmann, H.C. Optischer Gipsabdruck Hilft Bei Der Rückenanalyse. Süddeutscher Orthopädenkongress Kongressausgabe 1999, 2, 15.
  7. Harzmann, H.C. Stellenwert Der Videorasterstereographie Als Schulärztliche Screeningmethode von Skoliotischen Fehlhaltungen Und Strukturellen Skoliosen. PhD Thesis, Ludwig-Maximilians-Universität, Medizinischen Fakultät, München, Germany, 2000.
  8. Betsch, M.; Wild, M.; Jungbluth, P.; Thelen, S.; Hakimi, M.; Windolf, J.; Horstmann, T.; Rapp, W. The Rasterstereographic-Dynamic Analysis of Posture in Adolescents Using a Modified Matthiass Test. Eur. Spine J. 2010, 19, 1735–1739.
  9. Coblentz, A.M.; Herron, R.E. (Eds.) NATO Symposium on Applications of Human Biostereoietrics; Proceedings Volume; Society of Photo-Optical Instrumentation Engineers: Paris, France, 1980; Volume 166.
  10. Frobin, W. Rasterstereography: A Photogrammetric Method for Measurement of Body Surfaces. Photogramm. Eng. Remote. Sens. 1981, 47, 1717–1724.
  11. Hackenberg, L.; Hierholzer, E.; Pötzl, W.; Götze, C.; Liljenqvist, U. Rasterstereographic Back Shape Analysis in Idiopathic Scoliosis after Posterior Correction and Fusion. Clin. Biomech. 2003, 18, 883–889.
  12. Mangone, M.; Raimondi, P.; Paoloni, M.; Pellanera, S.; Di Michele, A.; Di Renzo, S.; Vanadia, M.; Dimaggio, M.; Murgia, M.; Santilli, V. Vertebral Rotation in Adolescent Idiopathic Scoliosis Calculated by Radiograph and Back Surface Analysis-Based Methods: Correlation between the Raimondi Method and Rasterstereography. Eur. Spine J. 2013, 22, 367–371.
  13. Schröder, J.; Schaar, H.; Korn, M.; Färber, I.; Ziegler, M.; Braumann, K.M.; Reer, R.; Mattes, K. Zur Sensitivität Und Reproduzierbarkeit Der Pedobarographie Mit Dem System PedoScan. Deutsche Zeitschrift Sportmedizin 2007, 58, 207.
  14. Seiberlich, N.; Gulani, V.; Campbell, A.; Sourbron, S.; Doneva, M.I.; Calamante, F.; Hu, H.H. Quantitative Magnetic Resonance Imaging; Academic Press: Cambridge, MA, USA, 2020; ISBN 978-0-12-817058-8.
  15. Yetişir, F. Local and Global SAR Constrained Large Tip Angle 3D KT-Points Parallel Transmit Pulse Design at 7 T, Massachusetts Institute of Technology: Massachusetts, 2014. Available online: https://dspace.mit.edu/handle/1721.1/87790 (accessed on 1 December 2021).
  16. Davids, J.R.; Chamberlin, E.; Blackhurst, D.W. Indications for Magnetic Resonance Imaging in Presumed Adolescent Idiopathic Scoliosis. J. Bone Jt. Surg. 2004, 86, 2187–2195.
  17. Maiocco, B.; Deeney, V.F.; Coulon, R.; Parks, P.F. Adolescent Idiopathic Scoliosis and the Presence of Spinal Cord Abnormalities. Spine 1997, 22, 2537–2541.
  18. Do, T.M.D.; Fras, C.M.D.; Burke, S.M.D.; Widmann, R.F.M.D.; Rawlins, B.M.D.; Boachie-Adjei, O.M.D. Clinical Value of Routine Preoperative Magnetic Resonance Imaging in Adolescent Idiopathic Scoliosis. J. Bone Jt. Surg. 2001, 83, 577–579.
  19. Wright, N. Imaging in Scoliosis. Arch. Dis. Child. 2000, 82, 38–40.
  20. Zhu, C.; Huang, S.; Song, Y.; Liu, H.; Liu, L.; Yang, X.; Zhou, C.; Hu, B.; Chen, H. Surgical Treatment of Scoliosis-Associated with Syringomyelia: The Role of Syrinx Size. Neurol. India 2020, 68, 299.
  21. Shih, R.Y.; Koeller, K.K. Intramedullary Masses of the Spinal Cord: Radiologic-Pathologic Correlation. RadioGraphics 2020, 40, 1125–1145.
  22. Bolognese, P.A.; Brodbelt, A.; Bloom, A.B.; Kula, R.W. Chiari I Malformation: Opinions on Diagnostic Trends and Controversies from a Panel of 63 International Experts. World Neurosurg. 2019, 130, e9–e16.
  23. Rogers, B.P.; Haughton, V.M.; Arfanakis, K.; Meyerand, M.E. Application of Image Registration to Measurement of Intervertebral Rotation in the Lumbar Spine. Magn. Reson. Med. 2002, 48, 1072–1075.
  24. Rogers, B.; Wiese, S.; Blankenbaker, D.; Meyerand, E.; Haughton, V. Accuracy of an Automated Method to Measure Rotations of Vertebrae from Computerized Tomography Data. Spine 2005, 30, 694–696.
  25. Carro, P.A. Magnetic Resonance Imaging in Children with Scoliosis. Semin. Musculoskelet. Radiol. 1999, 3, 257–266.
  26. Heinrich, A.; Reinhold, M.; Güttler, F.V.; Matziolis, G.; Teichgräber, U.K.-M.; Zippelius, T.; Strube, P. MRI Following Scoliosis Surgery? An Analysis of Implant Heating, Displacement, Torque, and Susceptibility Artifacts. Eur. Radiol. 2021, 31, 4298–4307.
  27. Ahmad, F.U.; Sidani, C.; Fourzali, R.; Wang, M.Y. Postoperative Magnetic Resonance Imaging Artifact with Cobalt-Chromium versus Titanium Spinal Instrumentation. J. Neurosurg. Spine 2013, 19, 629–636.
  28. Etemadifar, M.R.; Andalib, A.; Rahimian, A.; Nodushan, S.M.H.T. Cobalt Chromium-Titanium Rods versus Titanium-Titanium Rods for Treatment of Adolescent Idiopathic Scoliosis; Which Type of Rod Has Better Postoperative Outcomes? Rev. Assoc. Med. Bras. 2018, 64, 1085–1090.
  29. Buzug, T.M. Computed Tomography. In Springer Handbook of Medical Technology; Krame, R., Hoffmann, K.P., Pozos, R.S., Eds.; Springer Handbooks; Springer: Berlin/Heidelberg, Germany, 2011.
  30. Brenner, D.J.; Hall, E.J. Computed Tomography--an Increasing Source of Radiation Exposure. N. Engl. J. Med. 2007, 357, 2277–2284.
  31. Yawn, B.P.; Yawn, R.A.; Hodge, D.; Kurland, M.; Shaughnessy, W.J.; Ilstrup, D.; Jacobsen, S.J. A Population-Based Study of School Scoliosis Screening. JAMA 1999, 282, 1427–1432.
  32. Chen, K.; Zhai, X.; Sun, K.; Wang, H.; Yang, C.; Li, M. A Narrative Review of Machine Learning as Promising Revolution in Clinical Practice of Scoliosis. Ann. Transl. Med. 2021, 9, 67.
  33. Yang, J.; Zhang, K.; Fan, H.; Huang, Z.; Xiang, Y.; Yang, J.; He, L.; Zhang, L.; Yang, Y.; Li, R.; et al. Development and Validation of Deep Learning Algorithms for Scoliosis Screening Using Back Images. Commun. Biol. 2019, 2, 390.
  34. Pazos, V.; Cheriet, F.; Song, L.; Labelle, H.; Dansereau, J. Accuracy Assessment of Human Trunk Surface 3D Reconstructions from an Optical Digitising System. Med. Biol. Eng. Comput. 2005, 43, 11–15.
  35. Jaremko, J.L.; Poncet, P.; Ronsky, J.; Harder, J.; Dansereau, J.; Labelle, H.; Zernicke, R.F. Estimation of Spinal Deformity in Scoliosis From Torso Surface Cross Sections. Spine 2001, 26, 1583–1591.
  36. Komeili, A.; Westover, L.; Parent, E.C.; El-Rich, M.; Adeeb, S. Correlation Between a Novel Surface Topography Asymmetry Analysis and Radiographic Data in Scoliosis. Spine Deform. 2015, 3, 303–311.
  37. Ramirez, L.; Durdle, N.G.; Raso, V.J.; Hill, D.L. A Support Vector Machines Classifier to Assess the Severity of Idiopathic Scoliosis From Surface Topography. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 84–91.
  38. Bergeron, C.; Cheriet, F.; Ronsky, J.; Zernicke, R.; Labelle, H. Prediction of Anterior Scoliotic Spinal Curve from Trunk Surface Using Support Vector Regression. Eng. Appl. Artif. Intell. 2005, 18, 973–983.
  39. Liu, X.C.; Thometz, J.G.; Lyon, R.M.; Klein, J. Functional Classification of Patients with Idiopathic Scoliosis Assessed by the Quantec System. Spine 2001, 26, 1274–1279.
  40. Zhang, J.; Lou, E.; Hill, D.L.; Raso, J.V.; Wang, Y.; Le, L.H.; Shi, X. Computer-Aided Assessment of Scoliosis on Posteroanterior Radiographs. Med. Biol. Eng. Comput. 2010, 48, 185–195.
  41. Samuvel, B.; Thomas, V.; Mini, M.G.; Kumar, J.R. A Mask Based Segmentation Algorithm for Automatic Measurement of Cobb Angle from Scoliosis X-ray Image. In Proceedings of the 2012 International Conference on Advances in Computing and Communications, Cochin, India, 9–11 August 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 110–113.
  42. Zhang, J.; Li, H.; Lv, L.; Zhang, Y. Computer-Aided Cobb Measurement Based on Automatic Detection of Vertebral Slopes Using Deep Neural Network. Int. J. Biomed. Imaging 2017, 2017, 9083916.
  43. Wu, W.; Liang, J.; Du, Y.; Tan, X.; Xiang, X.; Wang, W.; Ru, N.; Le, J. Reliability and Reproducibility Analysis of the Cobb Angle and Assessing Sagittal Plane by Computer-Assisted and Manual Measurement Tools. BMC Musculoskelet. Disord. 2014, 15, 33.
  44. Shaw, M.; Adam, C.J.; Izatt, M.T.; Licina, P.; Askin, G.N. Use of the IPhone for Cobb Angle Measurement in Scoliosis. Eur. Spine J. 2012, 21, 1062–1068.
  45. Dollár, P.; Appel, R.; Belongie, S.; Perona, P. Fast Feature Pyramids for Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1532–1545.
  46. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation; Springer: Berlin/Heidelberg, Germany, 2015.
  47. Yongcheng, T.; Nian, W.; Fei, T.; Hemu, C. Automatic Measurement Algorithm of Scoliosis Cobb Angle Based on Deep Learning. J. Phys. Conf. Ser. 2019, 1187, 042100.
  48. Forsberg, D.; Lundström, C.; Andersson, M.; Vavruch, L.; Tropp, H.; Knutsson, H. Fully Automatic Measurements of Axial Vertebral Rotation for Assessment of Spinal Deformity in Idiopathic Scoliosis. Phys. Med. Biol. 2013, 58, 1775–1787.
  49. Anitha, H.; Prabhu, G.; Karunakar, A.K. Reliable and Reproducible Classification System for Scoliotic Radiograph Using Image Processing Techniques. J. Med. Syst. 2014, 38, 124.
  50. Anitha, H.; Prabhu, G.K. Automatic Quantification of Spinal Curvature in Scoliotic Radiograph Using Image Processing. J. Med. Syst. 2012, 36, 1943–1951.
  51. Sardjono, T.A.; Wilkinson, M.H.F.; Veldhuizen, A.G.; van Ooijen, P.M.A.; Purnama, K.E.; Verkerke, G.J. Automatic Cobb Angle Determination from Radiographic Images. Spine 2013, 38, E1256–E1262.
  52. Sun, H.; Zhen, X.; Bailey, C.; Rasoulinejad, P.; Yin, Y.; Li, S. Direct Estimation of Spinal Cobb Angles by Structured Multi-Output Regression. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone, IA, USA, 25–30 June 2017.
  53. Xue, W.; Islam, A.; Bhaduri, M.; Li, S. Direct Multitype Cardiac Indices Estimation via Joint Representation and Regression Learning. IEEE Trans. Med. Imaging 2017, 36, 2057–2067.
  54. Wu, H.; Bailey, C.; Rasoulinejad, P.; Li, S. Automated Comprehensive Adolescent Idiopathic Scoliosis Assessment Using MVC-Net. Med. Image Anal. 2018, 48, 1–11.
  55. Wang, L.; Xu, Q.; Leung, S.; Chung, J.; Chen, B.; Li, S. Accurate Automated Cobb Angles Estimation Using Multi-View Extrapolation Net.Medical Image Analysis. Med. Image Anal. 2019, 58, 101542.
  56. Watanabe, K.; Aoki, Y.; Matsumoto, M. An Application of Artificial Intelligence to Diagnostic Imaging of Spine Disease: Estimating Spinal Alignment from Moiré Images. Neurospine 2019, 16, 697–702.
  57. Choi, R.; Watanabe, K.; Jinguji, H.; Fujita, N.; Ogura, Y.; Demura, S.; Kotani, T.; Wada, K.; Miyazaki, M.; Shigematsu, H.; et al. CNN-Based Spine and Cobb Angle Estimator Using Moire Images. J. Med. Syst. 2017, 5, 135–144.
  58. Choi, R.; Watanabe, K.; Fujita, N.; Ogura, Y.; Matsumoto, M.; Demura, S.; Kotani, T.; Wada, K.; Miyazaki, M.; Shigematsu, H.; et al. Measurement of Vertebral Rotation from Moire Image for Screening of Adolescent Idiopathic Scoliosis. IEEE Trans. Image Electron. Vis. Comput. 2018, 6, 55–64.
  59. Kokabu, T.; Kanai, S.; Kawakami, N.; Uno, K.; Kotani, T.; Suzuki, T.; Tachi, H.; Abe, Y.; Iwasaki, N.; Sudo, H. An Algorithm for Using Deep Learning Convolutional Neural Networks with Three Dimensional Depth Sensor Imaging in Scoliosis Detection. Spine J. 2021, 21, 980–987.
  60. Sudo, H.; Kokabu, T.; Abe, Y.; Iwata, A.; Yamada, K.; Ito, Y.M.; Iwasaki, N.; Kanai, S. Automated Noninvasive Detection of Idiopathic Scoliosis in Children and Adolescents: A Principle Validation Study. Sci. Rep. 2018, 8, 17714.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback