Fuzzy Logic Control for Refrigeration Systems

Fuzzy Logic Control for Refrigeration Systems: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Engineering, Mechanical

Contributor:

Logic fuzzy systems are based on the human ability to think, which has allowed controllers to adapt better to systems by finding an approximation to their real behavior.

control strategies
energy saving
humidity
refrigeration systems

1. Introduction

Refrigeration systems based on vapor compression are widely used in different sectors, such as domestic, commercial, and industrial. In fact, in recent decades the demand for these refrigeration and air conditioning systems, RACs, has increased significantly, and it is estimated that there are around five billion systems in operation worldwide. Thus, the refrigeration sector represents one of the main energy consumers; it is estimated that these systems consume around 20% of the total electrical energy demanded worldwide [1].

Given the incipient deficiency of energy resources, saving the energy consumption by RACs has become an increasingly urgent area to address. Therefore, different strategies have been developed which have led to energy improvements; in addition to the above, mitigation of the environmental impact due to the use of RACs. These strategies include the use of alternative refrigerants with low greenhouse potential, GWP (Global warming potential) [2], or the use of nano refrigerants and nano lubricants [3]; the development of reliable profiles for RACs loads [4]; the use of new phase change materials [5]; the use of expanders [6]; the thermal design of heat exchange equipment [7]; and the inclusion of control systems [8], among many others. Consequently, control systems play a very important role in the operation of RACs.

2. Fuzzy Controller Design Applied to RACs

Logic fuzzy systems are based on the human ability to think, which has allowed controllers to adapt better to systems by finding an approximation to their real behavior. This has been observed mainly in those systems where their analytic functions are difficult to obtain. These controllers, through the creation of a database of knowledge with fuzzy linguistic expressions and rules, can make decisions about the control of a process using a method called inference. This method simulates the human thinking process allowing us to understand mathematically the knowledge represented in rules of the type IF-THEN to obtain an output value from the controller. In this sense, the inference method of Mamdani (Max-Min) is most commonly used in the design of fuzzy controls for the RACs. Another method also used in the field of refrigeration is the Sugeno method or Takagi-Sugeno-Kang, TSK. Figure 1 shows the typical structure of a fuzzy control system. It has four stages: fuzzification, rule base, inference engine, and defuzzification. During the fuzzification stage, the crisp inputs (the numeric values), by using membership functions, will determine the fuzzy values (μ(x)) in the range from zero to one. Then, the inference engine takes the fuzzy variables and evaluates the rules established in the rule base, and one or more fuzzy sets representing the output fuzzy variables can be obtained. Finally, defuzzification converts the fuzzy variables into crisp values that can be used by the actuator in a control system [20]. At this stage, it is possible to use different methods to perform this transformation from fuzzy values to real values.

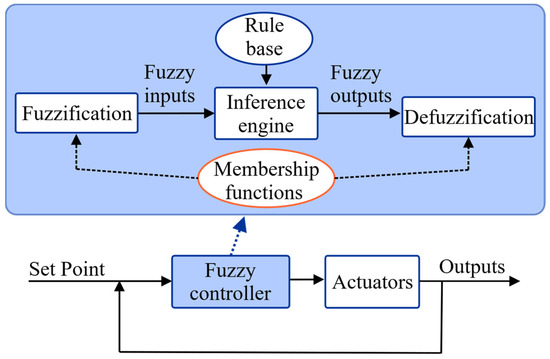
Figure 1. General scheme of a fuzzy controller.

Generally speaking, the fuzzy control applied to the RACs focuses on the control of temperature and humidity. Consequently, variables, such as the duty cycle, the electric frequency of the compressor, the opening of the expansion valve, and the flux of the refrigerant are manipulated. Because of the similarity between the controlled variables (temperature and humidity) and the manipulated variables (operating duration or compressor frequency), the design of controllers for the RACs shares some characteristics independently of the system to which it is applied. The first element corresponds to the design of the membership functions for the input and output variables of the fuzzy system. Figure 2 shows the fuzzy sets most used for the RACs, these present a combination of triangular and Gaussian functions. In these sets, two of the functions are placed at the ends and they correspond to trapezoidal functions (Figure 2a) or Gaussian functions (Figure 2b). In the study of the RACs, the triangular function is most commonly used around 70% of the published research papers present controllers using a combination of triangular functions. This is because a triangle or a trapezius often provides an adequate representation of the expert knowledge, and at the same time, these two shapes simplify significantly the computation process [21] and they can additionally improve the dynamics of the system [22]. However, Islam and Hossain [23] showed that the use of triangular or trapezoidal membership functions affects the performance of the controller and, in particular, for air conditioning systems, trapezoidal functions are the most suitable.

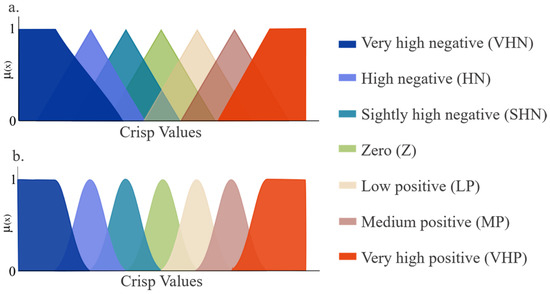
Figure 2. Membership function sets for the input and output variables. (a) trapezoidal functions; (b) Gaussian functions.

The set of the membership functions may depend directly on the variable or the error. With low frequency, sets of fuzzy functions in which the domain depends directly on the variable are presented. In these cases, the domain of the set of membership functions (or universe) includes all possible values that the variable can take. In most cases, there are sets in which the membership functions depend on the error, the derivative of the error, or the integral of the error. Therefore, the range of the set of functions exhibits negative and positive values. The range of the values that the universe can take is very diverse and depends on the range of the measurement of the variables that are taken into consideration for the design of each controller.

Additionally, it is very common in the design of a controller that the names of the linguistic variables are similar to the names of the membership functions. For instance, if the function is centered around zero, the name would be Z. On the other hand, if the function is positive, the name would be P. When the function is negative, the name could be N. In the same sense, it is customary to use the modifiers “very” (V), “medium” (M), “low” (L), etc. To establish some of the linguistic terms, such as “very positive” (VP) or “slightly low negative” (SLN), it is necessary to assign these names based on the number of functions in the controller. Table 1 shows a summary of the description of the linguistics variables most frequently used in the design of fuzzy logic controllers for the input and output variables.

Table 1. Linguistic variables frequently used in RACs.

Inputs			Outputs
Variable	Linguistic Term	Description	Variable	Linguistic Term	Description
Temperature	VHP	Very high positive	Compressor speed, airspeed, fan speed, opening percentage of EEV	VHS	Very high speed
	MP	Medium positive		MED	Medium
	LP	Low positive		SLH	Slightly high
	Z	Zero		VH	Very high
	SHN	Slightly high negative		NM	Normal
	HN	High negative		SLL	Slightly low
	VHN	Very high negative		VLS	Very low speed
Humidity	H	High		SLS	Slightly low speed
	VL	Very low		LS	Low speed
	SH	Slightly high		MS	Medium speed
	M	Medium		SHS	Slightly high speed
	L	Low		VLS	Very low speed
	SH	Slightly high		OFF	Off

The output variables in the fuzzy logic controllers in the RACs correspond to variables of the actuators. For instance, temperature control is performed by modifying mainly the speed of the compressor, the duty cycle of the compressor, and the opening of the expansion valves. For humidity control, it is regulated by modifying the speed of the fans or opening the gates. The fuzzy sets for the input and output variables generally coincide in quantity and shape. For the RACs, systems with five membership functions for the input and the output are generally designed. However, Almasani et al. [24] presented a set of membership functions with different quantities and shapes for the input and output variables, showing that it is not necessary to use the same type and number of functions to attain satisfactory results in temperature control. Additionally, Islam et al. [25] demonstrated that according to the defuzzification method, the behavior of the output variables is affected and values with considerable differences are obtained that directly affect the behavior of the system.

Fuzzy Logic Integrated with Other Control Systems for RACs

One of the advantages of fuzzy logic is its ease of integration with other controllers; this integration has shown an improvement in the regulation of process variables. One of the most common integrations in RACs is with Proportional Integral Derivate, PID, controllers. Figure 3 shows the general diagram of a fuzzy PID controller. This diagram shows the most frequent application in RACs, where fuzzy control supervises the adjustment of the constants kp, ki, and kd of the PID control, generating self-adjusting controls or adaptive controllers. There are also alternatives in the application of PID fuzzy controllers. For example, determining one or two PID control constants kp and ki or kp or kd [24], application of cascade controls [25]. There is also the possibility that fuzzy control regulates the output of the PID controller [26].

Figure 3. General scheme of a PID-fuzzy controller.

This entry is adapted from the peer-reviewed paper 10.3390/app12031302

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.