Topological and Dissipative Solitons in Liquid Crystals: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Physics, Condensed Matter
Contributor:
Yuan Shen

Solitons are self-sustained localized packets of waves in nonlinear media that propagate without changing shape. They are found everywhere in our daily life from nerve pluses in our bodies to eyes of storms in the atmosphere and even density waves in galaxies. Solitons in liquid crystals have received increasing attention due to their importance in fundamental physical science and potential applications in various fields. 

  • liquid crystal
  • soliton
  • toron
  • skyrmion
  • nematic
  • cholesteric
  • micro-cargo transport

1. Introduction

Nowadays, solitons have appeared in every branch of physics, such as nonlinear photonics [1], Bose-Einstein condensates [2], superconductors [3], and magnetic materials [4], just to name a few. Generally, solitons appear as self-organized localized waves that preserve their identities after pairwise collisions [5]. This ideal nonlinear property of solitons may enable distortion-free long-distance transport of matter or information and thus makes them considerably attractive to both fundamental research and technological applications [6][7][8].

Liquid crystals (LCs) are self-organized anisotropic fluids that are thermodynamically intermediate between the isotropic liquid and the crystalline solid, exhibiting the fluidity of liquids as well as the order of crystals [9][10]. Generally, LCs consist of anisotropic building blocks with rod- or disc-like shapes, which spontaneously orient in a specific direction on average, called director, n. As a typical nonlinear material, LCs have been broadly used as an ideal testbed for studying solitons, in which different kinds of solitons have been generated in the past five decades.

2. Early Works

The study of solitons in LCs was started in 1968 by Wolfgang Helfrich [11]. He theoretically modelled alignment inversion walls as static solitons in an infinite sample of nematic order. By applying a magnetic field, H, depending on the assumed orientation of the director at infinity, there are three types of possible walls, i.e., twist wall, splay-bend wall parallel to the applied field, and the splay-bend wall perpendicular to the field, which are analogous to the Bloch and Neel walls in ferromagnetics (Figure 1). Such a model was later improved by de Gennes who studied the boundary effects of the substrate and the movement of the walls [12].
Crystals 12 00094 g001 550
Figure 1. Schematic diagrams of different alignment inversion walls. (a) Twist wall. (b) Splay-bend wall parallel to the magnetic field. (c) Splay-bend wall vertical to the magnetic field. Reprinted with permission from Ref. [11]. Copyright 1968 American Physical Society.

3. Nematicons

Nematicons are self-focused light beams (spatial optical solitons) that propagate in nematic LCs. The beginning may date back to the early works by Braun et al. in which optical beams of complex structures, such as the formation of focal light spots, the onset of transverse beam undulations, and the development of multiple beam filaments, are realized by interacting a low-power laser beam with a nematic LC [13][14]. Compared to most materials, the nonlinear coefficient of nematic LC is extremely large (106 to 1010 times greater than that of typical optical materials such as CS2), making it an ideal system for investigating spatial optical solitons [13]. As shown in Figure 2, a linearly polarized beam propagates along the z-axis and enters a nematic cell. The polarization of the beam is parallel to the y-axis. 
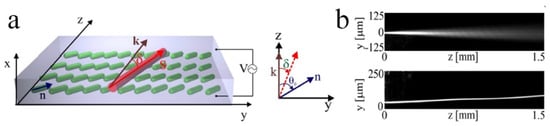
Crystals 12 00094 g005 550
Figure 2. (a) Schematic of the formation of a nematicon in a planar nematic LC cell. (b) Photographs of a propagating ordinary light beam (top) and a nematicon (bottom). Reprinted with permission from Ref. [15]. Copyright 2019 Optical Society of America.

4. Topological Solitons in Chiral Nematics

Topological solitons are continuous but topologically nontrivial field configurations embedded in uniform physical fields that behave like particles and cannot be transformed into a uniform state through smooth deformations [16]. They were probably first proposed by the great mathematician Carl Friedrich Gauss, who envisaged that localized knots of physical fields, such as electric or magnetic fields, could behave like particles [17]. Kelvin and Tait noticed the importance of this concept in physics and proposed one of the early models of atoms, in which they tried to explain the diversity of chemical elements as different knotted vortices [17]. Based on these theories, Hopf proposed the celebrated mathematical Hopf fibration [18], which was later applied to three-dimensional physical fields by Finkelstein [19] and led to the increasing interest of topological solitons to mathematicians and physicists. Nowadays, topological solitons have been investigated in many branches of physics such as instantons in quantum theory [20][21], vortices in superconductors [22], rotons in Bose-Einstein condensates [23], and Skyrme solitons in particle physics [24], etc. 
In CNLCs, topological solitons such as 2D merons and skyrmions (low-dimensional analogs of Skyrme solitons) can be generated and have recently received great attention. The molecules of a CNLC form a “layered” structure. Generally, by applying an electric field to a CNLC or sandwiching it between surfaces of homeotropic anchoring, the helical superstructure of the CNLC will be deformed, leading to the formation of string-like cholesteric fingers [25] and/or nonsingular solitonic field configurations [26]. The solitons are composed of a double-twist cylinder closed on itself in the form of a torus and coupled to the surrounding uniform field by point or line topological defects and are called “torons” (Figure 3a). The authors successfully demonstrated the structure and stability of the torons by the basic field theory of elastic director deformations and obtained the equilibrium field configuration and elastic energy of torons through numerical simulations. Later, the same authors reported the generation of 2D reconfigurable photonic structures composed of ensembles of torons [27][28][29]. In 2013, Chen et al. reported the generation of Hopf fibration (Figure 3c) in a CNLC by manipulating the two point defects of torons [30]. They demonstrate the relationship between Hopf fibration and torons through a topological visualization technique derived from the Pontryagin-Thom construction. In the following years, a variety of different kinds of skyrmionic solitons, such as half-skyrmions, twistion, skyrmion bags, skyrmion spin ice, skyrmion-dressed colloidal particles, and more complicated structures composed of torons, hopfions, and various disclinations, were realized and reported by different groups [31][32][33][34][35][36][37][38][39]. The self-assembly of torons (Figure 3d) [40][41][42] and hopfions in ferromagnetic LCs were later realized by Ackerman et al. [43]. Furthermore, the continuous transformation of 3D Hopf solitons [44] and the generation of 3D knots dubbed “heliknotons” (Figure 3e,f) [45] in CNLCs were reported by Tai et al. Due to the continuous twist of the director field within topological solitons, they can be used as optical devices for controlling and modulating the propagation of light [46][47][48][49]. 
Crystals 12 00094 g006 550
Figure 3. (a) Configuration of a toron. (b) Polarizing microscopy texture of different defect-proliferated torons. Reprinted with permission from Ref. [50]. Copyright 2010 Nature. (c) Flow lines and preimage surfaces of Hopf fibration. Reprinted with permission from Ref. [30]. Copyright 2013 American Physical Society. (d) Self-assembly of skyrmions. Reprinted with permission from Ref. [40]. Copyright 2015 Nature. (e) Knotted co-located half-integer vortex lines in a heliknoton. (f) Polarizing microscopy texture of heliknotons. Reprinted with permission from Ref. [45]. Copyright 2019 Science.

5. Dynamic Dissipative Solitons in Liquid Crystals

Dissipative solitons are stable localized solitary deviations of a state variable from an otherwise homogeneous stable stationary background distribution. They are generally powered by an external driver and vanish below a finite strength of the driver [51]. Experimentally, dissipative solitons were generated in the form of electric current filaments in a 2D planar gas-discharge system [52]. In LCs, different kinds of dissipative solitons have been generated and reported recently [53][54][55][56][57][58][59].
In 2018, Li et al. reported the formation of 3D dissipative solitons in an electrically driven nematic, which were called “director bullets” [53] or “directrons” [54] by the authors (Figure 4). These solitons were first reported by Brand et al. in 1997, and were called “butterflies”, but did not receive much attention at that time. The directrons (we will refer to them as “directrons” to distinguish them from other solitons) are self-confined localized director deformations. While the nematic aligns homogeneously outside the directrons, the director field is distorted and oscillates with the frequency of the applied AC electric field within the directrons. Such an oscillation breaks the fore-aft symmetry of the structure of the directrons and leads to the rapid propagation perpendicular to the alignment direction. 
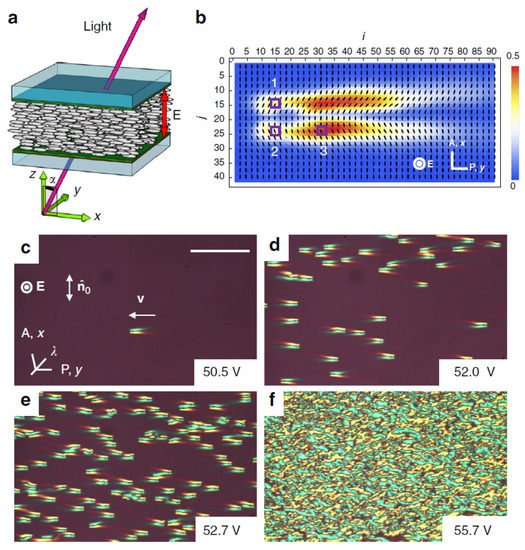
Crystals 12 00094 g008 550
Figure 4. Director bullets in a planar nematic cell. (a) Cell scheme. (b) Transmitted light intensity map and director distortions in the xy plane within a single bullet. (c–e) Polarizing microscopy of the director bullets at varied voltages. (f) Polarizing microscopy of the electro-hydrodynamic pattern. Scale bar 200 μm. Reprinted with permission from Ref. [53]. Copyright 2018 Nature.

6. Conclusions

Although recent studies of topological solitons and dissipative solitons have received great attention, many fundamental questions remain unanswered. For instance, the existence of topological solitons with higher dimensions in biaxial liquid crystal systems, a systematic classification of the topological solitons, the stability of the topological and dissipative solitons, the transformation between different topological solitons, the influence of the topological structure on the dynamics and interactions of topological solitons, the formation mechanism of the directrons, the role of ions played in the formation and motion of dissipative solitons, the influence of surface anchoring on the stability, formation and dynamics of the solitons, the effect of chirality on the structure and dynamics of the solitons, the interactions between solitons and colloidal particles, the self-assembly and collective behavior of the solitons, the existence of topological and dissipative soliton in lyotropic and active LC systems, the relation between the solitons in LCs and the solitons in other physical systems, etc. All these questions remain elusive and require further experimental and theoretical investigations to answer.
After over five decades of research, various solitons have been created and described in different liquid crystalline systems. This not only broadens the research and understanding of LCs, but also enhances our understanding of solitons in other physical systems. Furthermore, the solitons in LCs may even lead to novel phenomena, such as emergent collective motion of solitons [60][61], and applications, such as micro-cargo transport [56][57][62], optic processing [47][48], or fast LC displays [63]. 

This entry is adapted from the peer-reviewed paper 10.3390/cryst12010094

References

  1. Du, L.; Yang, A.; Zayats, A.V.; Yuan, X. Deep-subwavelength features of photonic skyrmions in a confined electromagnetic field with orbital angular momentum. Nat. Phys. 2019, 15, 650–654.
  2. Ray, M.W.; Ruokokoski, E.; Kandel, S.; Möttönen, M.; Hall, D. Observation of Dirac monopoles in a synthetic magnetic field. Nature 2014, 505, 657–660.
  3. Harada, K.; Matsuda, T.; Bonevich, J.; Igarashi, M.; Kondo, S.; Pozzi, G.; Kawabe, U.; Tonomura, A. Real-time observation of vortex lattices in a superconductor by electron microscopy. Nature 1992, 360, 51–53.
  4. Yu, X.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904.
  5. Scott, A.C.; Chu, F.Y.F.; McLaughlin, D.W. The soliton: A new concept in applied science. Proc. IEEE 1973, 61, 1443–1483.
  6. Bullough, R. Solitons. Phys. Bull. 1978, 29, 78.
  7. Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclassical Opt. 2005, 7, R53.
  8. Dauxois, T.; Peyrard, M. Physics of Solitons; Cambridge University Press: Cambridge, UK, 2006.
  9. De Gennes, P.-G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Oxford University Press: Oxford, UK, 1993; Volume 83.
  10. Shen, Y.; Dierking, I. Perspectives in Liquid-Crystal-Aided Nanotechnology and Nanoscience. Appl. Sci. 2019, 9, 2512.
  11. Helfrich, W. Alignment-Inversion Walls in Nematic Liquid Crystals in the Presence of a Magnetic Field. Phys. Rev. Lett. 1968, 21, 1518–1521.
  12. De Gennes, P. Mouvements de parois dans un nématique sous champ tournant. J. De Phys. 1971, 32, 789–792.
  13. Braun, E.; Faucheux, L.; Libchaber, A.; McLaughlin, D.; Muraki, D.; Shelley, M. Filamentation and undulation of self-focused laser beams in liquid crystals. EPL (Europhys. Lett.) 1993, 23, 239.
  14. Braun, E.; Faucheux, L.P.; Libchaber, A. Strong self-focusing in nematic liquid crystals. Phys. Rev. A 1993, 48, 611.
  15. Laudyn, U.A.; Kwaśny, M.; Karpierz, M.A.; Assanto, G. Electro-optic quenching of nematicon fluctuations. Opt. Lett. 2019, 44, 167–170.
  16. Manton, N.; Sutcliffe, P. Topological Solitons; Cambridge University Press: Cambridge, UK, 2004.
  17. Kauffman, L.H. Knots and Physics; World Scientific: Farrer Road, Singapore, 2001; Volume 1.
  18. Hopf, H. Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche. Math. Ann. 1931, 104, 637–665.
  19. Finkelstein, D. Kinks. J. Math. Phys. 1966, 7, 1218–1225.
  20. Shuryak, E.V. The role of instantons in quantum chromodynamics:(I). Physical vacuum. Nucl. Phys. B 1982, 203, 93–115.
  21. Shuryak, E.V. The role of instantons in quantum chromodynamics:(II). Hadronic structure. Nucl. Phys. B 1982, 203, 116–139.
  22. Abrikosov, A.A. Nobel Lecture: Type-II superconductors and the vortex lattice. Rev. Mod. Phys. 2004, 76, 975–979.
  23. O’dell, D.; Giovanazzi, S.; Kurizki, G. Rotons in gaseous Bose-Einstein condensates irradiated by a laser. Phys. Rev. Lett. 2003, 90, 110402.
  24. Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569.
  25. Oswald, P.; Baudry, J.; Pirkl, S. Static and dynamic properties of cholesteric fingers in electric field. Phys. Rep. 2000, 337, 67–96.
  26. Haas, W.E.L.; Adams, J.E. New optical storage mode in liquid crystals. Appl. Phys. Lett. 1974, 25, 535–537.
  27. Trushkevych, O.; Ackerman, P.; Crossland, W.A.; Smalyukh, I.I. Optically generated adaptive localized structures in confined chiral liquid crystals doped with fullerene. Appl. Phys. Lett. 2010, 97, 201906.
  28. Ackerman, P.J.; Qi, Z.; Smalyukh, I.I. Optical generation of crystalline, quasicrystalline, and arbitrary arrays of torons in confined cholesteric liquid crystals for patterning of optical vortices in laser beams. Phys. Rev. E 2012, 86, 021703.
  29. Smalyukh, I.I.; Kaputa, D.; Kachynski, A.V.; Kuzmin, A.N.; Ackerman, P.J.; Twombly, C.W.; Lee, T.; Trivedi, R.P.; Prasad, P.N. Optically generated reconfigurable photonic structures of elastic quasiparticles in frustrated cholesteric liquid crystals. Opt. Express 2012, 20, 6870–6880.
  30. Chen, B.G.-G.; Ackerman, P.J.; Alexander, G.P.; Kamien, R.D.; Smalyukh, I.I. Generating the Hopf fibration experimentally in nematic liquid crystals. Phys. Rev. Lett. 2013, 110, 237801.
  31. Ackerman, P.J.; Trivedi, R.P.; Senyuk, B.; van de Lagemaat, J.; Smalyukh, I.I. Two-dimensional skyrmions and other solitonic structures in confinement-frustrated chiral nematics. Phys. Rev. E 2014, 90, 012505.
  32. Ackerman, P.J.; Smalyukh, I.I. Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions. Phys. Rev. X 2017, 7, 011006.
  33. Ackerman, P.J.; Smalyukh, I.I. Reversal of helicoidal twist handedness near point defects of confined chiral liquid crystals. Phys. Rev. E 2016, 93, 052702.
  34. Nych, A.; Fukuda, J.-i.; Ognysta, U.; Žumer, S.; Muševič, I. Spontaneous formation and dynamics of half-skyrmions in a chiral liquid-crystal film. Nat. Phys. 2017, 13, 1215.
  35. Fukuda, J.-I.; Nych, A.; Ognysta, U.; Žumer, S.; Muševič, I. Liquid-crystalline half-Skyrmion lattice spotted by Kossel diagrams. Sci. Rep. 2018, 8, 1–8.
  36. Duzgun, A.; Nisoli, C. Artificial spin ice of liquid crystal skyrmions. arXiv 2019, arXiv:1908.03246.
  37. Foster, D.; Kind, C.; Ackerman, P.J.; Tai, J.-S.B.; Dennis, M.R.; Smalyukh, I.I. Two-dimensional skyrmion bags in liquid crystals and ferromagnets. Nat. Phys. 2019.
  38. Pandey, M.B.; Porenta, T.; Brewer, J.; Burkart, A.; Čopar, S.; Žumer, S.; Smalyukh, I.I. Self-assembly of skyrmion-dressed chiral nematic colloids with tangential anchoring. Phys. Rev. E 2014, 89, 060502.
  39. Porenta, T.; Čopar, S.; Ackerman, P.J.; Pandey, M.B.; Varney, M.C.M.; Smalyukh, I.I.; Žumer, S. Topological Switching and Orbiting Dynamics of Colloidal Spheres Dressed with Chiral Nematic Solitons. Sci. Rep. 2014, 4, 7337.
  40. Ackerman, P.J.; van de Lagemaat, J.; Smalyukh, I.I. Self-assembly and electrostriction of arrays and chains of hopfion particles in chiral liquid crystals. Nat. Commun. 2015, 6, 6012.
  41. Kim, Y.H.; Gim, M.-J.; Jung, H.-T.; Yoon, D.K. Periodic arrays of liquid crystalline torons in microchannels. RSC Adv. 2015, 5, 19279–19283.
  42. Sohn, H.R.O.; Liu, C.D.; Wang, Y.; Smalyukh, I.I. Light-controlled skyrmions and torons as reconfigurable particles. Opt. Express 2019, 27, 29055–29068.
  43. Ackerman, P.J.; Smalyukh, I.I. Static three-dimensional topological solitons in fluid chiral ferromagnets and colloids. Nat. Mater. 2016, 16, 426.
  44. Tai, J.-S.B.; Ackerman, P.J.; Smalyukh, I.I. Topological transformations of Hopf solitons in chiral ferromagnets and liquid crystals. Proc. Natl. Acad. Sci. USA 2018, 115, 921.
  45. Tai, J.-S.B.; Smalyukh, I.I. Three-dimensional crystals of adaptive knots. Science 2019, 365, 1449.
  46. Varanytsia, A.; Chien, L.-C. Photoswitchable and dye-doped bubble domain texture of cholesteric liquid crystals. Opt. Lett. 2015, 40, 4392–4395.
  47. Hess, A.J.; Poy, G.; Tai, J.-S.B.; Žumer, S.; Smalyukh, I.I. Control of light by topological solitons in soft chiral birefringent media. Phys. Rev. X 2020, 10, 031042.
  48. Poy, G.; Hess, A.J.; Smalyukh, I.I.; Žumer, S. Chirality-enhanced periodic self-focusing of light in soft birefringent media. Phys. Rev. Lett. 2020, 125, 077801.
  49. Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Subnanowatt Opto-Molecular Generation of Localized Defects in Chiral Liquid Crystals. Adv. Mater. 2014, 26, 4242–4246.
  50. Smalyukh, I.I.; Lansac, Y.; Clark, N.A.; Trivedi, R.P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2009, 9, 139.
  51. Purwins, H.-G.; Bödeker, H.; Amiranashvili, S. Dissipative solitons. Adv. Phys. 2010, 59, 485–701.
  52. Bödeker, H.; Röttger, M.; Liehr, A.; Frank, T.; Friedrich, R.; Purwins, H.-G. Noise-covered drift bifurcation of dissipative solitons in a planar gas-discharge system. Phys. Rev. E 2003, 67, 056220.
  53. Li, B.-X.; Borshch, V.; Xiao, R.-L.; Paladugu, S.; Turiv, T.; Shiyanovskii, S.V.; Lavrentovich, O.D. Electrically driven three-dimensional solitary waves as director bullets in nematic liquid crystals. Nat. Commun. 2018, 9, 2912.
  54. Li, B.-X.; Xiao, R.-L.; Paladugu, S.; Shiyanovskii, S.V.; Lavrentovich, O.D. Three-dimensional solitary waves with electrically tunable direction of propagation in nematics. Nat. Commun. 2019, 10, 3749.
  55. Aya, S.; Araoka, F. Kinetics of motile solitons in nematic liquid crystals. Nat. Commun. 2020, 11, 1–10.
  56. Shen, Y.; Dierking, I. Dynamics of electrically driven solitons in nematic and cholesteric liquid crystals. Commun. Phys. 2020, 3, 1.
  57. Shen, Y.; Dierking, I. Dynamic dissipative solitons in nematics with positive anisotropies. Soft Matter 2020, 16, 5325.
  58. Shen, Y.; Dierking, I. Electrically driven formation and dynamics of swallow-tail solitons in smectic A liquid crystals. Mater. Adv. 2021.
  59. Lavrentovich, O.D. Design of nematic liquid crystals to control microscale dynamics. Liq. Cryst. Rev. 2020, 8, 59–129.
  60. Sohn, H.R.O.; Liu, C.D.; Smalyukh, I.I. Schools of skyrmions with electrically tunable elastic interactions. Nat. Commun. 2019, 10, 4744.
  61. Sohn, H.R.; Liu, C.D.; Voinescu, R.; Chen, Z.; Smalyukh, I.I. Optically enriched and guided dynamics of active skyrmions. Opt. Express 2020, 28, 6306–6319.
  62. Li, B.-X.; Xiao, R.-L.; Shiyanovskii, S.V.; Lavrentovich, O.D. Soliton-induced liquid crystal enabled electrophoresis. Phys. Rev. Res. 2020, 2, 013178.
  63. Lam, L.; Prost, J. Solitons in Liquid Crystals; Springer Science & Business Media: New York, NY, USA, 2012.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback