Orientation Detection Mechanism Based on Artificial Visual System: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Computer Science, Artificial Intelligence
Contributor:
Yuki Todo

As an important part of the nervous system, the human visual system can provide visual perception for humans. The research on it is of great significance to improve our understanding of biological vision and the human brain. Orientation detection, in which visual cortex neurons respond only to linear stimuli in specific orientations, is an important driving force in computer vision and biological vision. However, the principle of orientation detection is still unknown. 

  • artificial visual system
  • orientation detection
  • dendritic neuron model
  • convolutional neural network
  • noise resistance

1. Introduction

The study of orientation detection mechanism and visual nervous system provides a strong clue for us to further understand the functional mechanism of the human brain. David Hubel and Torsten Wiesel discovered directed selection cells in the primary visual cortex (V1) in 1981 and presented a simple but powerful model of how such directed selection arises from non-selective thalamic cortical inputs [1][2]. The model has become a central frame of reference for understanding cortical computing and its underlying mechanisms [3]. Hubel and Wiese won the Nobel Prize for Medicine for their landmark discovery of orientational preference and other related work. In this period, they conducted a series of studies and experiments about cortex cells on rabbits and monkeys and observed some biological phenomena: (1) The visual cortex cells especially respond to rectangular light spot and slit; (2) there is a simple type of cortical cells in the visual cortex that only respond to specific angle stimulation in the receptive field [4][5]. The properties of these neurons are called orientation selectivity. These neurons can simply be fired to a specific orientation but with no or little response to other orientations. Orientation detection is one of the basic functions of the visual system and helps us recognize the environment around us and make judgments and choices.
However, questions remain unanswered as to how the computations performed in V1 represent computations performed in many areas of the cerebral cortex, and whether V1 contains highly specific and unique mechanisms for computing orientation from retinal images [6][7][8]. Recent studies provide strong, indirect support that dendrites play important and possibly crucial roles in visually computing invertebrates [9][10][11][12][13][14][15][16][17][18]. The nonlinear interaction of dendrite trees is to use Boolean logic and representation (together), or (separation), rather than (negation), or soft minimum, even for multiplication, and soft maximum [19][20][21][22]. Experiments also show that a single neocortex pyramidal neuron of dendrites can categorize linear, inseparable inputs, the calculation of which is traditionally believed to need a multilayer network [23][24][25].
Almost 60 years ago, Hubel and Wiesel indeed observed that individual cortical cells have directional selectivity, that is, individual neurons respond selectively to certain orientations of the bar or grating and not to others. However, the details of these individual neurons are still unknown [26]. How, to what extent, and by what mechanism does cortical processing affect orientation choice remain unclear. In this paper, we propose a new quantitative mechanism to explain how a circuit model based on V1 cortical anatomy produces directional selectivity. We first hypothesized the presence of locally directed detection neurons in the visual nervous system. Each local orientation detection neuron receives its photoreceptor input, selectively takes adjacent photoreceptor input, and computes to respond only to the orientation of the selected adjacent photoreceptor input. Based on the dendrite neuron model, the local orientation detection neuron is realized and extended to a multiorientation detection neuron. To demonstrate the effectiveness of our mechanism, we conducted a series of experiments on a total dataset of 252,000 images of different shapes, sizes, and positions, moving in different orientations of motion. Computer simulation shows that the machine can detect the motion orientation well in all experiments.

2. Mechanism

2.1. Dendritic Neuron Model

Artificial neural network (ANN) has been a research hotspot in the field of artificial intelligence since the 1980s [27][28]. By stimulating brain synaptic connection structure and information technology processing mechanisms through mathematical learning models, neural networks play important roles in various fields, such as medical diagnosis, stock index prediction, and autonomous driving, in which they have shown excellent performance [29][30][31].
All of these networks use the traditional McCulloch–Pitts neuron model as their basic computing unit [32]. However, the McCulloch–Pitts model did not take into account the nonlinear mechanism of dendrites [33]. At the same time, recent research on dendrites in neurons plays a key role in the overall calculation, which provides strong support to future research [34][35][36][37][38][39][40][41]. Koch, Poggio, and Torre proposed that, in the dendrites of retinal ganglion cells, if activated inhibitory synapses are closer to the cell body than excitatory synapses, excitatory synapses will be intercepted [42][43]. Thus, the interaction between synapses on the dendritic branch can be regarded as a logical AND operation. The branch node can sum up the current coming from the branch, which can be simulated as a logical OR operation. The outputs of branch nodes are directed to the cell body (soma). When the signal exceeds the threshold, the cell will be fired and send a signal through its axon to other neurons. Figure 1a shows an ideal δ cell model. Here, if the inhibition interaction is described as a NOT gate, the output of the δ cell model can be expressed as follows:
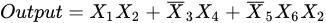
where X1, X2, X4, and X6 denote excitatory inputs, whereas X3 and X5 denote inhibitory inputs. Each input can be simulated as a logical 0 or 1 signal. Therefore, the cell body (soma) signal will generate a logical 1 signal only in the following three cases: (i) X1 = 1 and X2 = 1; (ii) X3 = 0 and X4 = 1; (iii) X5 = 0, X6 = 1 and X2 = 1. In addition, the γ cell receives signals from the excitatory and inhibitory synapses, which is presented in Figure 1b. The output of the γ cell model can be described as follows:
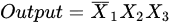
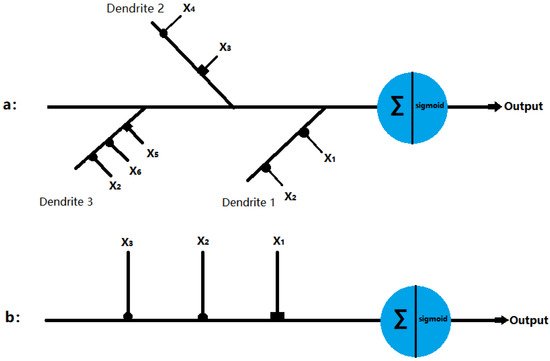
Electronics 11 00054 g001 550
Figure 1. Structure of the dendritic neuron model with inhibitory inputs (■) and excitatory inputs (•): (a) δ cell and (b) γ cell.

2.2. Local Orientation Detection Neuron

In this section, we describe in detail the structure of the neuron and how it detects orientation. We hypothesized that simple ganglion neurons can provide orientation information by detecting light signals in themselves and around them.
For the sake of simplicity, we set the receptive field as a two-dimensional MXN region; each region corresponds to the smallest visible region [44]. When light hits a receptive region, the electrical signal is transmitted through its photoreceptors to ganglion cells, which process various visual information. The input signal can be represented as Xij, where i and j represent the positions of the two-dimensional receptive field. For the input signal Xij, we used the current neuron and the eight surrounding regions, and the local orientation information can be obtained, as presented in Figure 2.
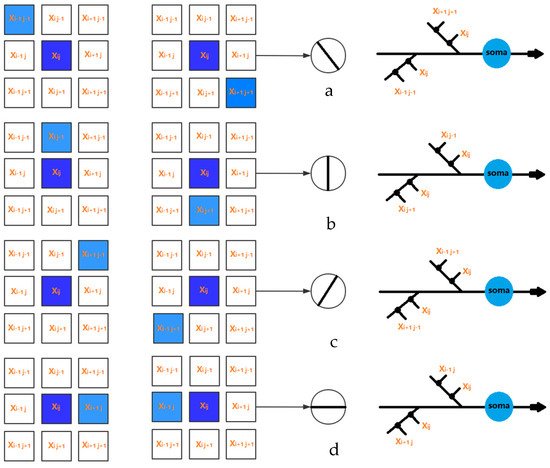
Electronics 11 00054 g002 550
Figure 2. The local orientation detection neurons for (a) 0 degree, (b) 45 degree, (c) 90 degree, and (d) 135 degree.
In this study, the receptive field was set to a 3 × 3 matrix. Thus, the active states of eight neurons corresponding to four orientation information can be obtained, where 135° and 315° are 135° inclines, 90° and 270° are vertical, 45° and 225° are 45° inclines, and 0° and 180° are horizontal. In addition, more orientation information can be achieved with the increasing size of the receptive field.

2.3. Global Orientation Detection

As mentioned above, locally directed detection neurons interact by performing the effects of light falling on their receiving fields. Here, we hypothesized that the local information can be used to determine the global orientation. Therefore, we can measure the activity intensity of all local orientations of the detected neurons in the receptive field and make orientation judgments by summarizing the output of neurons in different orientations.
To measure the activity intensity of local orientational detection neurons in the two-dimensional receptive field (MXN), we have four possible solutions as follows: (1) One neuron scheme—it is assumed that there is only one local orientation detection of retinal ganglion neuron, the neuron scans eight orientations for each location; (2) multiple neuron scheme—it is assumed that eight different neurons scan eight adjacent positions in different orientations to provide local orientation information; (3) neuron array scheme—it is assumed that a number of non-overlapping neurons slide on the receptive field to provide orientation information; (4) all-neuron scheme—we assumed that each photoreceptor corresponds to a 3 × 3 receptive field, which has its local orientation in eight positions. Therefore, in each receptive field, local orientation detection neurons can extract basic orientation information. Then, the global orientation can be judged by local orientation information. To understand the mechanism by which the system performs orientational detection, we used a simple two-dimensional (5 × 5) image with a target angle of 45 degrees, which is shown in Figure 3. Without losing generality, we used the first solution. Local detection of retinal ganglion neurons scan each position from (1,1) to (5,5) on the receptive field and generate local orientation information. As shown in Figure 3, the activation level of 45° neurons is the highest, which is consistent with the target.
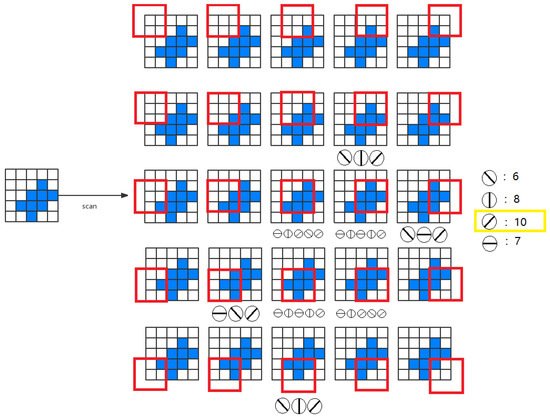
Electronics 11 00054 g003 550
Figure 3. An example of global orientation detection.

2.4. Artificial Visual System (AVS)

The visual system consists of the sensory organs (the eyes), pathways connecting the visual cortex, and other parts of the central nervous system. In the visual system, local visual feature detection neurons can extract local orientation information and other basic local visual features. These features are then combined by subsequent layers to detect higher-order features. Based on this mechanism, we developed an artificial vision system (AVS), as shown in Figure 4. Layer 1 neurons (also known as the layer of local feature detector neurons (LFDNs) correspond to neurons in the V1 region of the cortex, such as local orientation detection neurons, which extract basic local visual features. These features are then sent to a subsequent layer (also known as the global feature-detecting neuron layer) corresponding to the middle temporal (MT) region of the primate brain to detect higher-order features, for example, the global orientation of an object. Neurons in this layer can be the sum of the output of neurons in the simple layer 1, such as the neurons for orientation detection, motion direction detection, motion speed detection, and binocular vision perception; this can be a one-layer, a two-layer corresponding to V4 and V6, or a three-layer corresponding to V2, V3, and V5, and even a multilayer network, for example, for pattern recognition. It is worth noting that AVS is a feedforward neural network, and any feedforward neural network can be trained by error backpropagation. The difference between AVS and traditional multilayer neural networks and convolutional neural networks is that LFDNs of AVS layer 1 can be designed in advance according to prior knowledge, so in most cases, they do not need to learn. Even if learning is required, AVS learning can start from a good starting point, which can greatly improve the efficiency and speed of learning. In addition, the hardware implementation of AVS is simpler and more efficient than CNN, requiring only simple logical calculations for most applications.
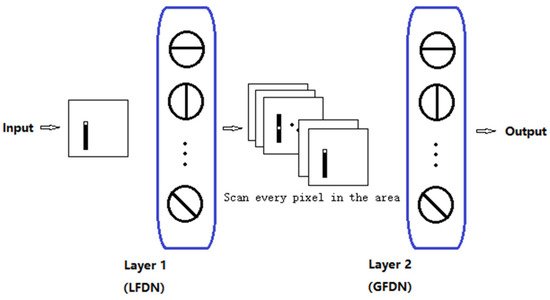
Electronics 11 00054 g004 550
Figure 4. Artificial visual system (AVS).

This entry is adapted from the peer-reviewed paper 10.3390/electronics11010054

References

  1. Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154.
  2. Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574–591.
  3. Gilbert, C.D.; Li, W. Adult visual cortical plasticity. Neuron 2012, 75, 250–264.
  4. Hubel, D.H.; Wiesel, T.N. Exploration of the primary visual cortex, 1955–1978. Nature 1982, 299, 515–524.
  5. Hubel, D.H.; Wiesel, T.N. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968, 195, 215–243.
  6. Jin, J.; Wang, Y.; Swadlow, H.A.; Alonso, J.M. Population receptive fields of ON and OFF thalamic inputs to an orientation column in visual cortex. Nat. Neurosci. 2011, 14, 232–238.
  7. Priebe, N.J.; Ferster, D. Mechanisms of neuronal computation in mammalian visual cortex. Neuron 2012, 75, 194–208.
  8. Wilson, D.E.; Whitney, D.E.; Scholl, B.; Fitzpatrick, D. Orientation selectivity and the functional clustering of synaptic inputs in primary visual cortex. Nat. Neurosci. 2016, 19, 1003–1009.
  9. McLaughlin, D.; Shapley, R.; Shelley, M.; Wielaard, D.J. A neuronal network model of macaque primary visual cortex (v1): Orientation selectivity and dynamics in the input layer 4cα. Proc. Natl. Acad. Sci. USA 2000, 97, 8087–8092.
  10. Chen, C.; Tonegawa, S. Molecular genetic analysis of synaptic plasticity, activity-dependent neural development, learning, and memory in the mammalian brain. Annu. Rev. Neurosci. 1997, 20, 157–184.
  11. Golding, N.L.; Spruston, N. Dendritic sodium spikes are variable triggers of axonal action potentials in hippocampal CA1 pyramidal neurons. Neuron 1998, 21, 1189–1200.
  12. Häusser, M.; Spruston, N.; Stuart, G.J. Diversity and dynamics of dendritic signaling. Science 2000, 290, 739–744.
  13. Martina, M.; Vida, I.; Jonas, P. Distal initiation and active propagation of action potentials in interneuron dendrites. Science 2000, 287, 295–300.
  14. Schwindt, P.C.; Crill, W.E. Local and propagated dendritic action potentials evoked by glutamate iontophoresis on rat neocortical pyramidal neurons. J. Neurophysiol. 1997, 77, 2466–2483.
  15. Stuart, G.; Spruston, N.; Sakmann, B.; Häusser, M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci. 1997, 20, 125–131.
  16. Velte, T.J.; Masland, R.H. Action potentials in the dendrites of retinal ganglion cells. J. Neurophysiol. 1999, 81, 1412–1417.
  17. Taylor, W.; Vaney, D.I. New directions in retinal research. Trends Neurosci. 2003, 26, 379–385.
  18. Fried, S.I.; Münch, T.A.; Werblin, F.S. Mechanisms and circuitry underlying directional selectivity in the retina. Nature 2002, 420, 411–414.
  19. Oesch, N.; Euler, T.; Taylor, W.R. Direction-selective dendritic action potentials in rabbit retina. Neuron 2005, 47, 739–750.
  20. Koch, C. Biophysics of Computation: Information Processing in Single Neurons; Oxford University Press: Oxford, UK, 2004.
  21. Silver, R.A. Neuronal arithmetic. Nat. Rev. Neurosci. 2010, 11, 474–489.
  22. Todo, Y.; Tamura, H.; Yamashita, K.; Tang, Z. Unsupervised learnable neuron model with nonlinear interaction on dendrites. Neural Netw. 2014, 60, 96–103.
  23. Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; John Wiley and Sons: Hoboken, NJ, USA, 1949.
  24. Gidon, A.; Zolnik, T.A.; Fidzinski, P.; Bolduan, F.; Papoutsi, A.; Poirazi, P.; Holtkamp, M.; Vida, I.; Larkum, M.E. Dendritic action potentials and computation in human layer 2/3 cortical neurons. Science 2020, 367, 83–87.
  25. Ramon y Cajal, S. Histologie du Système Nerveux de l’Homme et des Vertébrés; Maloine: Paris, France, 1911; Volume 2, pp. 153–173.
  26. Poirazi, P.; Brannon, T.; Mel, B.W. Pyramidal neuron as two-layer neural network. Neuron 2003, 37, 989–999.
  27. Hubel, D.H.; Wiesel, T.N. Receptive fields of optic nerve fibres in the spider monkey. J. Physiol. 1960, 154, 572–580.
  28. Hsu, K.-L.; Gupta, H.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530.
  29. Hassoun, M.H.; Intrator, N.; McKay, S.; Christian, W. Fundamentals of artificial neural networks. Comput. Phys. 1996, 10, 137.
  30. Al-Shayea, Q.K. Artificial neural networks in medical diagnosis. Int. J. Comput. Sci. Issues 2011, 8, 150–154.
  31. Khashei, M.; Bijari, M. An artificial neural network (p,d,q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489.
  32. Guresen, E.; Kayakutlu, G.; Daim, T.U. Using artificial neural network models in stock market index prediction. Expert Syst. Appl. 2011, 38, 10389–10397.
  33. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133.
  34. London, M.; Häusser, M. Dendritic computation. Annu. Rev. Neurosci. 2005, 28, 503–532.
  35. Agmon-Snir, H.; Carr, C.E.; Rinzel, J. The role of dendrites in auditory coincidence detection. Nat. Cell Biol. 1998, 393, 268–272.
  36. Anderson, J.C.; Binzegger, T.; Kahana, O.; Martin, K.A.C.; Segev, I. Dendritic asymmetry cannot account for directional responses of neurons in visual cortex. Nat. Neurosci. 1999, 2, 820–824.
  37. Artola, A.; Brocher, S.; Singer, W. Different voltage-dependent thresholds for inducing long-term depression and long-term potentiation in slices of rat visual cortex. Nat. Cell Biol. 1990, 347, 69–72.
  38. Euler, T.; Detwiler, P.; Denk, W. Directionally selective calcium signals in dendrites of starburst amacrine cells. Nat. Cell Biol. 2002, 418, 845–852.
  39. Magee, J.C. Dendritic integration of excitatory synaptic input. Nat. Rev. Neurosci. 2000, 1, 181–190.
  40. Single, S.; Borst, A. Dendritic integration and its role in computing image velocity. Science 1998, 281, 1848–1850.
  41. Spruston, N.; Stuart, G.; Hausser, M. Dendritic integration. In Dendrites; Stuart, G., Spruston, N., Hausser, M., Eds.; Oxford University Press: Oxford, UK, 2008.
  42. Dringenberg, H.C.; Hamze, B.; Wilson, A.; Speechley, W.; Kuo, M.-C. Heterosynaptic facilitation of in vivo thalamocortical long-term potentiation in the adult rat visual cortex by acetylcholine. Cereb. Cortex 2006, 17, 839–848.
  43. Koch, C.; Poggio, T.; Torre, V. Nonlinear interactions in a dendritic tree: Localization, timing, and role in information processing. Proc. Natl. Acad. Sci. USA 1983, 80, 2799–2802.
  44. Koch, C.; Poggio, T.; Torre, V. Retinal ganglion cells: A functional interpretation of dendritic morphology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1982, 298, 227–263.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback