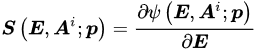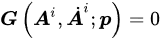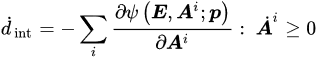Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Biomedical
Biomechanical investigations of surgical procedures and devices are usually developed by means of human or animal models. The exploitation of computational methods and tools can reduce, refine, and replace (3R) the animal experimentations for scientific purposes and for pre-clinical research. The computational model of a biological structure characterizes both its geometrical conformation and the mechanical behavior of its building tissues. Model development requires coupled experimental and computational activities. Medical images and anthropometric information provide the geometrical definition of the computational model. Histological investigations and mechanical tests on tissue samples allow for characterizing biological tissues’ mechanical response by means of constitutive models. The assessment of computational model reliability requires comparing model results and data from further experimentations. Computational methods allow for the in-silico analysis of surgical procedures and devices’ functionality considering many different influencing variables, the experimental investigation of which should be extremely expensive and time consuming.
- computational methods
- constitutive model
- dental implantology
- surgery
1. Introduction
Cooperation among clinicians and bioengineers has historically proved its efficacy and strength by providing tools, devices and methodologies for the optimization of health-care systems, devices, procedures and approaches [1]. With specific regard to the field of surgery, the combination of the typical rationalism of engineers and the creativity of surgeons led to novel and unimaginable evolutions and solutions [2][3]. Nowadays, a challenge pertains to the 3R approach, as reduce, refine and replace, to the use of animal models for scientific purposes and pre-clinical research. The 3R approach greatly influences common procedures for the definition, the design, the optimization, the reliability assessment and the certification of surgical procedures, instrumentations and devices. Aiming at this ethical and mandatory 3R approach, the competences and the skills of bioengineers can play a meaningful role [4]. Computational biomechanics provides structural modeling tools that allow for simulating the mechanical behavior of anatomical regions and the interaction phenomena occurring among such biological structures and surgical instrumentations [5] and/or prosthetic devices [6]. The accuracy and the reliability of computational methods continuously improve, because of the advancements in modelling research and the increase in computational power. In this sense, in-silico analyses and simulations can actually replace, reduce and refine experimentations on animal models [7].
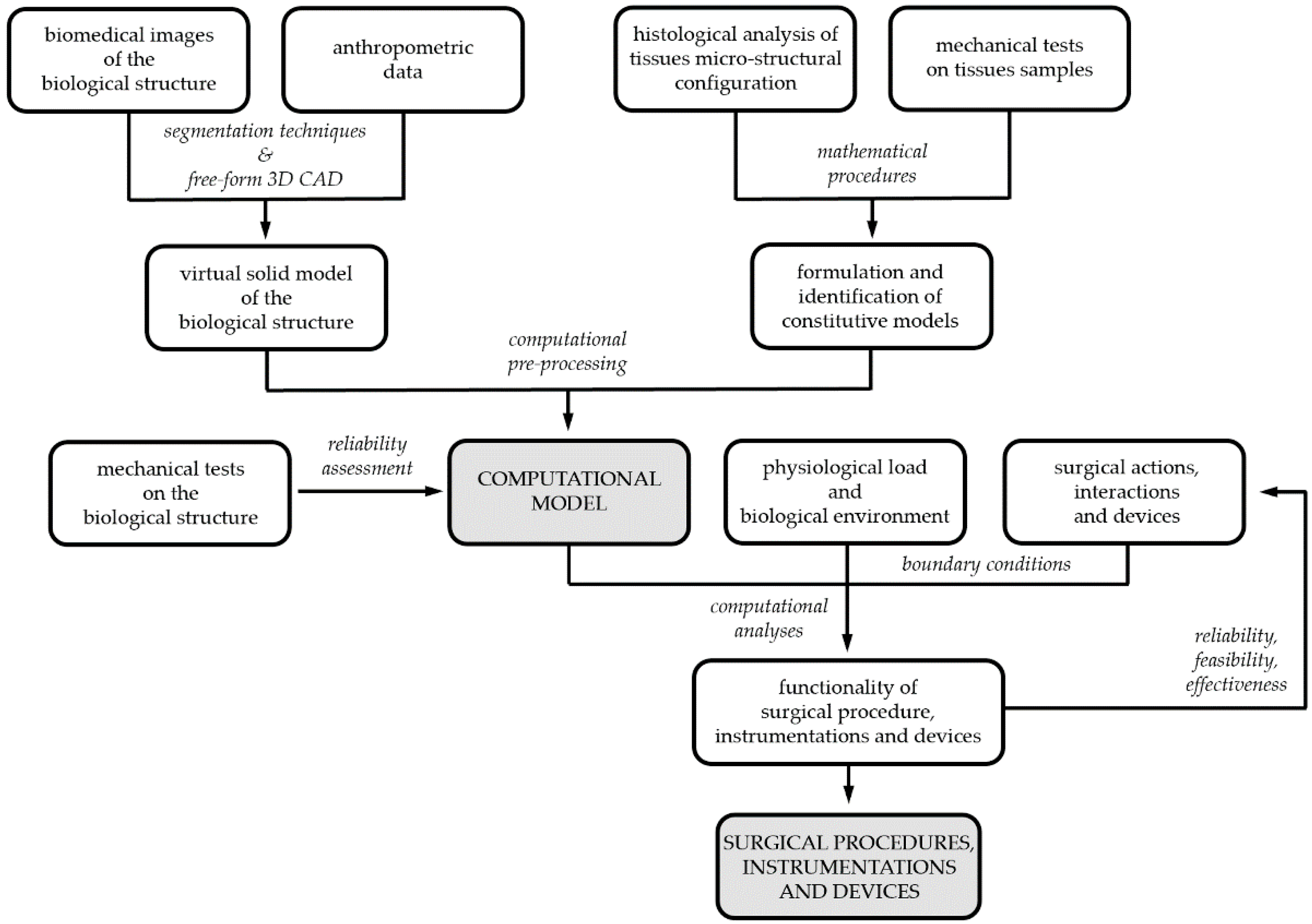
Developing the biomechanical model of a biological structure requires the characterization of both the geometrical conformation of the anatomical district, by means of virtual modelling techniques, and the mechanical behavior of building tissues, by means of constitutive investigations. Coupled experimental and computational activities are usually adopted to reach such a goal (Figure 1) [8]. Experimentations are mandatory for models’ definition, identification and reliability assessment [9]. Biomedical images from tomographic techniques, such as CT and/or MRI, together with anthropometric information lead to 3D CAD virtual models, whose discretization by finite element pre-processing software provides the geometrical definition of the computational model. The constitutive analysis of biological tissues requires information about both tissues micro-structural configuration, from histological investigation, and tissues’ mechanical behavior, from experimental tests on tissue samples. Finally, the assessment of computational model reliability requires comparing model results and data from further experimentations, which must be performed on the entire biological structure. According to the 3R approach, experimentations can be frequently performed on samples from animal models, as wastes from local abattoirs, and human surgical scraps.
Figure 1. Biomechanical models and computational techniques for surgery: coupled experimental and computational activities for model’s definition, identification and validation; model exploitation for designing, optimizing and certifying surgical procedures, instrumentations and devices.
2. Overview on Computational Modeling of Biological Structures
The biomechanical model of a biological structure aims at describing its mechanical behavior, as the deformation of the structure when mechanical loads act on the structure itself. Fundamental balance principles, such as the conservation of mass, equilibrium of forces and equilibrium of momenta, govern such evolution by means of partial differential equations. External loads and constraints specify the boundary conditions of the problem [10]. The complexity of the problem usually denies the analytical approach, and numerical methods, as the finite element method, must be adopted [11][12]. Practically, numerical methods transpose the differential problem into an algebraic problem, which is suitable for computational implementation and processing.
The development of the computational model of a biological structure requires the geometrical definition, which is achieved by means of virtual solid and finite element models, and the mechanical characterization of the building tissues by means of constitutive formulations. Boundary conditions specify the surgical actions. Moreover, the specific analysis techniques and computational strategies must be addressed.
3. Geometrical Characterization of Biological Structures
Three-dimensional virtual solid models of biological structures are usually developed by processing images from tomographic or histo-anatomical techniques together with anthropometric data. CT and MRI are typical tomographic technologies, which capture contiguous series of image slices. A slice defines a cut through the scanned biological structure and different slices are performed according to a settled thickness. The pixels of the image slice provide measurements of local material properties. Regions of homogeneous pixel values usually represent the inner portions of anatomical elements, whereas strong variations of pixel values identify tissue boundaries. Concatenating image slices leads a three-dimensional image stack, and anatomical elements can be traced between adjacent images. Virtual solid models of anatomical elements are extrapolated by means of segmentation procedures and 3D CAD free-form operations [13].
The next step of geometrical modelling pertains to finite element discretization, the fundamental issues of which are element topology and mesh density [12]. Mesh density is usually a compromise between the accuracy of results and computational effort. Non-uniform mesh density is frequently assumed; refined finite element discretization may be provided considering specific regions of the model, where the geometry is particularly complex or a more accurate solution is required [14].
4. Constitutive Analysis of Biological Tissues’ Mechanics
The constitutive model defines the mechanical response of a material by means of mathematical relationships, which specify the stress that the material experiences in terms of other field functions, such as the strain history [10][15]. The constitutive analysis of a biological tissue requires experimentally investigating both the microstructural arrangement and the mechanical behavior [8]. Complex and hierarchical microstructural configurations characterize biological tissues, the organizations of which are optimized to fulfill their specific mechanical functions. Microstructural rearrangement processes establish the phenomenological mechanical behavior of the material, as the response that the material exhibits during mechanical tests and, more generally, during mechanical loading. Microstructural information and data from experimental activities suggest the mathematical formulation of the constitutive model, which must be defined in the framework of the axiomatic theory of constitutive laws. The axiomatic theory provides for the following general rules [10]:
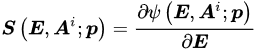
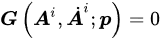
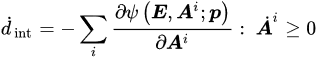
where E and S are appropriate and corresponding strain and stress tensors, respectively. Material straining entails energy consumption, as the work of the stress. Such energy is partially stored into the material in a recoverable form; the material will give it back in the form of mechanical work. The remaining part of the work of the stress is dissipated. From a microstructural point of view, material straining leads to modifications of the microstructural configuration and energy adsorption. Such microstructural modifications may be reversible, leading to recoverable energy storage; otherwise, irreversible modifications entail energy dissipation. Furthermore, friction phenomena may occur during microstructural modifications, providing further energy dissipation in heat. The development of dissipative phenomena, as the irreversible microstructural modifications and the friction effects, is described by means of internal variables Ai. From a phenomenological point of view, the internal variables may describe plastic strains, damage effects, non-equilibrated viscous stress components, etc. The Helmholtz free energy ψ evaluates the recoverable stored energy, which is a function of the material strain history in terms of the strain E and the internal variables Ai. Differentiation operations lead to the stress–strain relationship (Equation (1)). Algebraic differential equations G specify the evolution of internal variables with the strain history (Equation (2)). The Helmholtz free energy ψ and the evolution equations G must satisfy the dissipation rule (Equation (3)), which states that the energy dissipated during the strain history, as dint, has to increase or remain constant.
A particular class of constitutive equations—a class that includes elastic and, more precisely, hyperelastic formulations—assumes the absence of dissipative phenomena (dint remains constant). All the work of the stress is recoverably stored and is evaluated by the Helmholtz free energy. According to the dissipation rule (Equation (3)) and to the stress–strain relationship (Equation (1)), the Helmholtz free energy ψ and the stress S are functions of the strain E only; the Helmholtz free energy ψ is a potential of the strain E and is denominated strain energy function W. Otherwise, the dissipated energy dint increases during the strain history, and the material is said to have inelastic or dissipative behavior.
The vector of constitutive parameters p is related to the properties of the specific material (i.e., elastic constants, viscous parameters, yielding and hardening constants, damage limits, etc.). Once the model mathematical formulation has been defined, the next step of the constitutive analysis pertains to the identification of such parameters. The action is usually based on an inverse analysis by assuming a stress–strain history given by experimental data, designed at the purpose, and estimating the parameters that yield the best fit with analytical or computational results based on the assumed constitutive model. Aiming at the univocal identification of parameters, the required experimental situations must be accurately defined [3].
5. Computational Analysis Techniques
Biomechanical investigations aim at analyzing the response of the biological structure when specific actions are applied. Boundary conditions define such actions, together with motion constraints and interaction phenomena among the biological structure and surrounding environment and/or objects.
The biomechanical analysis may concern dynamic or quasi-static problems [11]. A dynamic approach is required if significant inertial effects occur, otherwise static procedures are suitable. A further issue pertains to the linearity or nonlinearity of the problem. Linear problems involve small displacements and strains, linear constitutive relationships, and linear boundary conditions. Otherwise, the mechanical problem is nonlinear. The numerical formulation of the problem entails the transposition of a differential problem to the solution of algebraic equations. The linearity or nonlinearity of the problem entails linearity or nonlinearity of numerical algebraic procedures. Greater computational effort characterizes nonlinear problems, because iterative solution algorithms are mandatory. Finally, the biomechanical problem may involve other physical phenomena, such as fluid dynamics, thermal, electromagnetic and/or diffusion processes. Multiphysics techniques provide coupled approaches in the numerical solution of such multiple interacting physical domains.
This entry is adapted from the peer-reviewed paper 10.3390/bioengineering7020048
References
- Huiskes, R.; Chao, E.Y.S. A survey of finite element analysis in orthopedic biomechanics: The first decade. J. Biomech. 1983, 16, 385–409.
- Payan, Y. Biomechanics Applied to Computer Assisted Surgery; Research Signpost: Kerala, India, 2005.
- Carniel, E.L.; Fontanella, C.G.; Polese, L.; Merigliano, S.; Natali, A.N. Computational tools for the analysis of mechanical functionality of gastrointestinal structures. Technol. Health Care 2013, 21, 271–283.
- Carusi, A. In silico medicine: Social, technological and symbolic mediation. HUMANA. MENTE J. Studies 2016, 9, 67–86.
- Carniel, E.L.; Frigo, A.; Fontanella, C.G.; De Benedictis, G.M.; Rubini, A.; Barp, L.; Pluchino, G.; Sabbadini, B.; Polese, L. A biomechanical approach to the analysis of methods and procedures of bariatric surgery. J. Biomech. 2017, 56, 32–41.
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. Biomechanical analysis of the interaction phenomena between artificial urinary sphincter and urethral duct. Int. J. Numer. Method Biomed. Eng. 2020, 36, e3308.
- Viceconti, M.; Henney, A.; Morley-Fletcher, E. In silico clinical trials: How computer simulation will transform the biomedical industry. Int. J. Clin. Trials 2016, 3, 37–46.
- Carniel, E.L.; Gramigna, V.; Fontanella, C.G.; Stefanini, C.; Natali, A.N. Constitutive formulations for the mechanical investigation of colonic tissues. J. Biomed. Mater. Res. A 2014, 102, 1243–1254.
- Henninger, H.B.; Reese, S.P.; Anderson, A.E.; Weiss, J.A. Validation of computational models in biomechanics. Proc. Inst. Mech. Eng. H 2010, 224, 801–812.
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Hoboken, NJ, USA, 2000; Chapter 6; pp. 205–304.
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013.
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000.
- Young, P.G.; Beresford-West, T.B.; Coward, S.R.; Notarberardino, B.; Walker, B.; Abdul-Aziz, A. non-linear viscoelastic laws for soft biological tissues. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 3155–3173.
- Zhang, Y.J. Geometric Modeling and Mesh Generation from Scanned Images; Taylor & Francis Group: Abingdon, UK, 2016.
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: Berlin/Heidelberg, Germany, 1998; Chapter 10; pp. 336–366.
This entry is offline, you can click here to edit this entry!
