Direct Torque Controllers in Five-Phase Electrical Drives

Direct Torque Controllers in Five-Phase Electrical Drives: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Engineering, Electrical & Electronic

Contributor:

Machines with more than three phases are called multiphase machines, which provide a better current distribution among phases, and lower current harmonic production in the power converter, than conventional three-phase machines. However, multiphase drive applications require the development of complex controllers to regulate the torque (or speed) and flux of the machine. In this regard, direct torque controllers have appeared as a viable alternative due to their easy formulation and high flexibility to incorporate control objectives.

direct torque control
multiphase
electrical drives

1. Introduction

Electric drives are the basis of locomotive traction, electric ship propulsion, electric aircraft with various auxiliary functions (e.g., fuel pumps, starter/generator solutions, etc.), and renewable energy production. Although conventional three-phase drives represent the principal choice for industrial applications, multiphase ones have recently aroused the interest of practitioner engineers and researchers in the field. Any energy conversion system formed by a multiphase electric machine and converter and regulated by a certain control technique is called a multiphase drive. The first application of such a system, particularly for a five-phase drive, was used in the late 1960s ^[1], showing the advantages of multiphase systems over conventional three-phase ones. The main interest in the proposal was that the higher number of phases yields a torque ripple three times lower with respect to the equivalent three-phase case due to a better power distribution per phase, this being one of the most reported problems in conventional drives at that time. However, it was not until the end of the 20th and the beginning of the 21st centuries that the interest of researchers in multiphase machines was renewed due to two main reasons. First, the development of high-power and high-frequency semiconductors and, consequently, the appearance of pulse width modulation (PWM) methods to control the ON and OFF states of these electronic devices, as well as the energy conversion process. Second, there is the development of microelectronic technology and the appearance of powerful electronic devices with the ability to implement control algorithms in real time, such as digital signal processors (DSPs) and field-programmable gate arrays (FPGAs).

Notwithstanding the above, the crucial reason for the renewed interest in multiphase drives can be found in the intrinsic benefits that they provide versus the conventional three-phase ones. These benefits are based on the extra degrees of freedom introduced by the higher number of phases and are principally the following:

The fault-tolerant capability against a fault situation in the machine and/or the power converter, first presented in ^[2]. An n-phase machine can operate after one or several fault occurrences without any external equipment, as long as the number of healthy phases remains greater than or equal to three (assuming a single isolated neutral connection). Consequently, the system reliability is enhanced at the expense of a reduction in the post-fault electrical torque production.
The capability of increasing the power density in healthy operation by injecting specific current harmonics, exposed in ^[3]. This is possible in certain multiphase machine configurations based on concentrated windings, where the lower current harmonic components can be used to increase the torque production.

Although field-oriented control (FOC) methods, based on decoupled control of the flux and electromagnetic torque and assisted by modulation stages, can be considered as the most popular control technique for conventional and multiphase drives ^[4]^[5], direct control techniques have recently been presented as interesting competitors ^[6]^[7]^[8]. The essence of direct controllers is to eliminate any form of modulation, forcing the states of the power switches to rapidly track a reference value. Then, the meaning of ‘direct control’ techniques is related to control strategies without the intervention of a pulse width modulation or any other form of modulation, providing control commands that are applied directly to the power converter. As a main consequence, direct controllers, being direct torque controllers (DTC) are the most extended industrial alternative, can favor fast torque responses and control robustness with respect to the variation of the electrical parameters of the machine. In this regard, DTC appears to be a viable (from a commercial perspective) control alternative in conventional three-phase drives due to an easy formulation and high flexibility to incorporate different control objectives. However, the use of DTC in multiphase drives is restricted in normal operation due to the impossibility of regulating more than two degrees of freedom (electrical torque and stator flux).

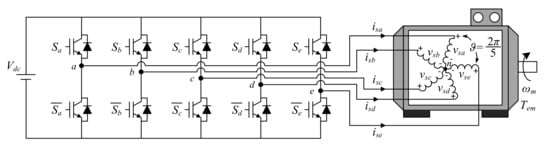
2. Five-Phase Distributed Windings Induction Motor Drive Using a Conventional Two-Level VSI

A graphical representation of the analyzed system is shown in Figure 1. It is based on a five-phase Induction Machine (IM) with a squirrel-cage rotor and symmetrically distributed stator windings (spatial equal displacement between windings) fed by a DC power supply through a five-phase two-level voltage source inverter (VSI).

Figure 1. Schematic diagram.

Figure 2 shows the two-dimensional projections obtained for every vector, identified with the decimal number equivalent of their respective switching state [S_a S_b S_c S_d S_e]^T expressed in binary logic (1 or 0), being S_a and S_e the most and the least significant bits, respectively. These vectors uniformly divide the space that they occupy in 10 sectors with a separation of π/5 between them. Likewise, active voltage vectors can be classified according to their magnitude in long (0.647 V_dc), medium (0.4 V_dc), and short (0.247 V_dc) vectors. The switching states that generate long vectors in the α–β plane correspond to those that generate short vectors in the plane x–y and vice versa. The switching states corresponding to vectors of medium magnitude in the α–β plane, also generate medium vectors in the plane x–y. Null vectors are generated by the same switching states in both planes. This transformation allows for a detailed study of the harmonic components, since they are projected in certain planes. In particular, the fundamental frequency together with the harmonics of order 10 k ± 1 (k = 0, 1, 2, etc.) are mapped in the α–β plane, while the harmonics of order 10 k ± 3 are related to the plane x–y. The homopolar component and harmonics of order 5 k are projected on the z-axis.

Figure 2. Mapping of the phase stator voltages of the two-level five-phase VSI in the α–β (left graph) and x–y (right graph) planes.

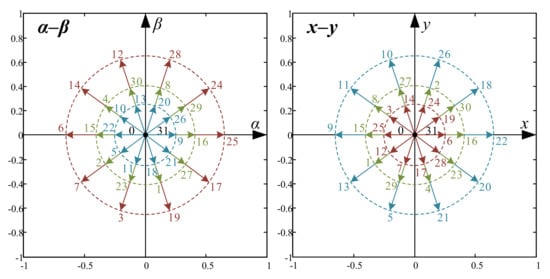
3. DTC in Five-Phase Drives

Direct Torque Control is a well-known strategy for three-phase electrical drives. It was presented in the mid-1980s by Takahashi ^[9] and Depenbrock ^[10], showing fast flux and torque responses, as well as more robustness with respect to the variation of the electrical parameters of the machine and generating a high-torque/flux ripple and harmonic current content, compared to the more standard field-oriented control technique. The operating principle is based on an off-line look-up table, which is used to select the stator voltage to be applied to the machine. The selection is made taking into account the position of the flux vector and the stator flux and electromagnetic torque error signals, obtained from the difference between reference and estimated values and processed using hysteresis comparators. Another disadvantage of DTC that should be considered from the analysis of its operating principle is that it does not generate a constant switching frequency. In fact, this switching frequency is variable and depends on the operating point and the bandwidth of the hysteresis controllers. Note, however, that DTC schemes have been proposed to also be used with PI regulators and space vector PWM methods (see ^[11]), to compensate for the variable switching frequency and reduce the torque and flux ripple.

DTC has been commercialized ^[12] and extended to the case of multiphase drives in recent times, considering different types of machines ^[13]^[14], machine neutral connections ^[15]^[16], and drives without speed sensors ^[17]. In the case of multiphase drives, since the controller has only two freedom degrees (stator flux and electromagnetic torque), there is no chance of regulating the current and voltage components in the orthogonal α–β and x–y planes. In this sense, some DTC strategies have been developed that satisfy this additional requirement, controlling the current and voltage components in the α–β plane while reducing at the same time the current and voltage components in the x–y plane. For example, in ^[18]^[19], a modification of the traditional control scheme is proposed, performing a two-step search to minimize the effect of low-order harmonics. Alternatively, the use of virtual vectors has been suggested to reduce current distortion ^[17]. Some criteria have also been included in the selection process within the look-up table to improve its performance in the low-speed region and an optimization between the two zero vectors to minimize the average switching frequency obtained ^[20]. On the other hand, and based on the virtual vectors defined in ^[17], different DTC schemes are presented defining new virtual vectors and avoiding the use of the zero vector to reduce the common-mode voltage generated by the VSI in ^[21]^[22], to improve open-phase fault operations in ^[23], or to avoid any reconfiguration of the controller when open-phase faults appear ^[24].

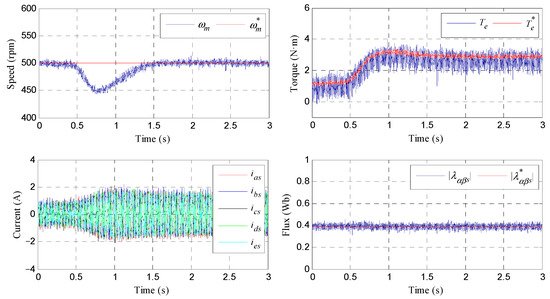
4.1. Steady-State Operation

First, the performance of the system in steady-state operation at 500 rpm is analyzed in Figure 3 and Figure 4, where different load torques are applied (1 N·m in Figure 3 and 2.75 N·m in Figure 4). The reference and measured values are colored red and blue, respectively. The speed and electrical torque responses are shown in the upper rows, where it is appreciated that the controller works well and the mechanical speed is successfully maintained in the reference value. Note that the electrical torque is mathematically estimated using the machine model, which produces some estimation errors. The reference and estimated stator flux in the regulated α–β plane are then shown in the second row, where it can be observed that the estimated stator flux values coincide with their references. Lastly, the measured stator currents are depicted in the last two rows, where it is appreciated that the α–β stator current vector describes a circular trajectory, with nearly null x–y stator current components. Therefore, the control goals are met using the DTC controller in steady-state operation because the results obtained can be extended to different reference speed and load torques.

Figure 3. Experimental steady-state operation test where the reference speed is settled at 500 rpm and a load torque of 1 N·m is applied. Upper row: speed and torque responses. Second row: stator flux waveforms. Third row: current trajectories of the stator in the α–β and x–y planes. Last row: stator phase currents.

Figure 4. Experimental steady-state operation test where the reference speed is set at 500 rpm and a load torque of 2.75 N·m is applied. Upper row: speed and torque responses. Second row: stator flux waveforms. Third row: current trajectories of the stator in the α–β and x–y planes. Last row: stator phase currents.

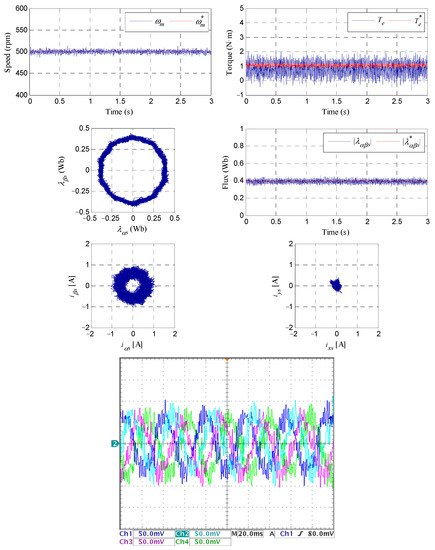
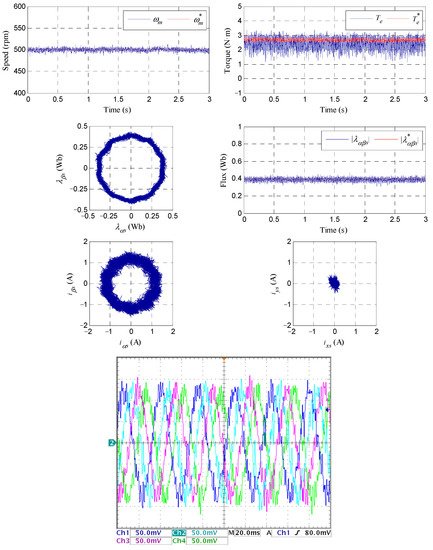
4.2. Load Torque Rejection

Then load torque rejection tests were performed. The results obtained are summarized in Figure 5, where the reference speed is 500 rpm and the coupled DC machine imposes a heavy load torque within the system limits at t = 0.5 s. A drop in the speed is observed when the load is suddenly applied; although, the controller successfully manages this disturbance, upper-left plot. The estimated electrical torque is also regulated to be the referred one in steady and transient states, as shown in the upper right figure, while stator phase currents increase to manage the increment in the load (see bottom-left timing diagram). The estimated stator flux value is regulated in steady and transient states to coincide with the references, as can be appreciated in the bottom right figure. Then, these results, which summarize the ones obtained under different operating conditions, prove a controlled electrical torque in the multiphase drive. Note that flat lines are also observed in the x–y plane polar diagrams of the stator current, similar to the ones shown in Figure 3 and Figure 4.

Figure 5. Experimental response of the controlled system in a load torque rejection test. The reference speed is 500 rpm and a load torque is applied at 0.5 s. The upper row shows the speed and torque responses. The lower row shows the stator current waveform and modulus of the stator flux during the test.

This entry is adapted from the peer-reviewed paper 10.3390/app112411964

References

Warg, E.E.; Härer, H. Preliminary investigation of an inventor-fed 5-phase induction motor. Proc. Inst. Electr. Eng. 1969, 116, 980–984.
Jahns, T.M. Improved reliability in solid-state AC drives by means of multiple independent phase drive units. IEEE Trans. Ind. Appl. 1980, IA-16, 321–331.
Toliyat, H.A.; Lipo, T.A.; White, J.C. Analysis of a concentrated winding induction machine for adjustable speed drive applications. I. Motor analysis. IEEE Trans. Energy Convers. 1991, 6, 679–683.
Barrero, F.; Duran, M.J. Recent advances in the design, modeling, and control of multiphase machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458.
Duran, M.J.; Barrero, F. Recent advances in the design, modeling, and control of multiphase machines—Part II. IEEE Trans. Ind. Electron. 2016, 63, 459–468.
Bermúdez, M.; Martín, C.; González, I.; Duran, M.J.; Arahal, M.R.; Barrero, F. Predictive current control in electrical drives: An illustrated review with case examples using a five-phase induction motor drive with distributed windings. IET Electr. Power Appl. 2020, 14, 1291–1310.
Arahal, M.R.; Martin, C.; Barrero, F.; Duran, M.J. Assessing variable sampling time controllers for five-phase induction motor drives. IEEE Trans. Ind. Electron. 2020, 67, 2523–2531.
Arahal, M.R.; Satué, M.G.; Barrero, F.; Ortega, M.G. Adaptive Cost Function FCSMPC for 6-Phase IMs. Energies 2021, 14, 5222.
Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, IA-22, 820–827.
Depenbrock, M. Direct self-control (DSC) of inverter-fed induction machine. IEEE Trans. Power Electron. 1988, 3, 420–429.
Fei, Y.; Xiaofeng, Z.; Minzhong, Q.; Chengdong, D. The direct torque control of multiphase permanent magnet synchronous motor based on low harmonic space vector PWM. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT-2008), Chengdu, China, 21–24 April 2008; pp. 1–5.
ABB Group. DTC: A Motor Control Technique for All Seasons. ABB White Paper. 2015. Available online: http://library.e.abb.com/public/0e07ab6a2de30809c1257e2d0042db5e/ABB_WhitePaper_DTC_A4_20150414.pdf (accessed on 27 October 2021).
Hadiouche, D.; Razik, H.; Rezzoug, A. On the modeling and design of dual-stator windings to minimize circulating harmonic currents for VSI fed AC machines. IEEE Trans. Ind. Appl. 2004, 40, 506–515.
Buja, G.S.; Kazmierkowski, M.P. Direct torque control of PWM inverter-fed AC motors—A survey. IEEE Trans. Ind. Electron. 2004, 51, 744–757.
Kianinezhad, R.; Nahid, B.; Betin, F.; Capolino, G.A. A novel Direct Torque Control (DTC) method for dual three phase induction motors. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT 2006), Mumbai, India, 15–17 December 2006; pp. 939–943.
Kianinezhad, R.; Alcharea, R.; Nahid, B.; Betin, F.; Capolino, G.A. A novel direct torque control (DTC) for six-phase induction motors with common neutrals. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2008), Ischia, Italy, 11–13 June 2008; pp. 107–112.
Zheng, L.; Fletcher, J.E.; Williams, B.W.; He, X. A Novel Direct Torque Control Scheme for a Sensorless Five-Phase Induction Motor Drive. IEEE Trans. Ind. Electron. 2011, 58, 503–513.
Parsa, L.; Toliyat, H.A. Sensorless Direct Torque Control of Five-Phase Interior Permanent-Magnet Motor Drives. IEEE Trans. Ind. Appl. 2007, 43, 952–959.
Gao, Y.; Parsa, L. Modified Direct Torque Control of Five-Phase Permanent Magnet Synchronous Motor Drives. In Proceedings of the 22nd Annual IEEE Applied Power Electronics Conference and Exposition (APEC 2007), Anaheim, CA, USA, 25 February–1 March 2007; pp. 1428–1433.
Gao, L.; Fletcher, J.E.; Zheng, L. Low-Speed Control Improvements for a Two-Level Five-Phase Inverter-Fed Induction Machine Using Classic Direct Torque Control. IEEE Trans. Ind. Electron. 2011, 58, 2744–2754.
Riveros, J.A.; Duran, M.J.; Barrero, F.; Toral, S. Direct torque control for five-phase induction motor drives with reduced common-mode voltage. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society (IECON 2012), Montreal, QC, Canada, 25–28 October 2012; pp. 3616–3621.
Tatte, Y.N.; Aware, M.V. Direct Torque Control of Five-Phase Induction Motor with Common-Mode Voltage and Current Harmonics Reduction. IEEE Trans. Power Electron. 2017, 32, 8644–8654.
Chikondra, B.; Muduli, U.R.; Behera, R.K. An Improved Open-Phase Fault-Tolerant DTC Technique for Five-Phase Induction Motor Drive Based on Virtual Vectors Assessment. IEEE Trans. Ind. Electron. 2021, 68, 4598–4609.
Barrero, F.; Bermúdez, M.; Durán, M.J.; Salas, P.; González-Prieto, I. Assessment of a Universal Reconfiguration-less Control Approach in Open-Phase Fault Operation for Multiphase Drives. Energies 2019, 12, 4698.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.