1. Definitions

The principal concepts discussed here are various types of topological groups, Lie groups, and Pro-Lie Groups.

All topological spaces considered here satisfy the Hausdorff separation axiom.

A topological group is a group defined on a topological space such that the defining operations multiplication and inversion are continuous functions. It is called a locally compact group if the underlying space is locally compact, a connected group, if it is connected, and an almost connected group, if the space of connected components is compact. In one form or another, the technical concept of a Lie group (Sophus M. Lie, 1842-1847, see^[21]), is very well-known. There is a variety of definitions of Lie group:

1. A Lie group is a group on a differential (smooth, analytic) manifold with its defining operations being differentiable (smooth, analytic).
2. A Lie group is a topological group G together with a completely normable Lie algebra (see ^[3]) g whose local Campbell-Hausdorff multiplication (^{[3][12][18][19]}) matches the defining operations of G near the identity (details e.g. in^[18]) via an exponential function exp: g → G (see^[18]). g is called the Lie algebra of G.
3. A topological group G is a linear Lie group if it may be identified with a closed subgroup of the group of invertible elements of a completely normable algebra with identity such that there is a closed vector subspace g of A also closed under the operation 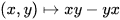such that the exponential function of A maps some neighborhood of 0 in g homeomorphically onto a neighborhood of 1 in G. (See^[19], Definition 5.32, p. 171.)

In finite dimensions Definition 1 and 2 are equivalent and every linear Lie group is a Lie group and every Lie group is locally isomorphic to a linear Lie group. Traditionally, it is usually assumed that a Lie group G is finite dimensional, i.e., its Lie algebra is finite-dimensional.

Finally, a topological group G is called a pro-Lie group if there is a collection of normal subgroups N of G such that G/N is a finite dimensional Lie group and the natural function G → ∏ {G/N:  N∈ Ν} yields an isomorphism of topological groups from G onto its image. The class of pro-Lie groups has a thoroughly developed “Lie Theory” (see ^[18]). Totally disconnected compact groups are profinite and thus are pro-Lie groups but have no Lie theory.

2. Some history

Groups emerged in 1770 in the work Joseph-Louis Lagrange (1736-1813) and in 1799 in the attempt to solving quintic equations by Paolo Ruffini (1765-1822). Abstract groups go back to Augustin-Louis Cauchy (1789-1857), Niels Henrik Abel (1802-1829), and Évariste Galois (1811-1832). The word “group” was first used by Galois (in French). The beginnings of Topology reach far back, however, in the words of August Ferdinan Möbius (1790-1868) it was Jules Henri Poincaré (1854-1912) who “gave topology wings”. The latter's first article appeared in 1895. Johann Benedict Listing (1808-1882) introduced the German word Topologie in 1847. While Topology as an independent area had not yet crystallized, Geometry was quite present, when Felix Klein (1849-1925) and Sophus Lie (1842-1899) (and followers like Friedrich Engel (1861-1941) and Wilhelm Karl Joseph Killing (1847-1923)) founded what became known as the theory of Lie groups. Algebra, geometry, and analysis were thoroughly mixed into the genesis of Lie group theory. In 1900, at the International Congress of Mathematicians in Paris, David Hilbert (1862-1943) predicted crucial developments in mathematics in the 20th century by formulating 23 open problems. By that time topology was quite present in the minds of mathematicians. Hilbert formulated for instance, his famous Fifth Problem (expressed in current terminology): Is a topological group on a euclidean manifold a Lie group? He envisioned a positive answer. However, it took a little over half a century to confirm his vision. Yet this half century advanced the research of topological groups enormously. The most consequential steps were:

(i) the discovery of fundamental properties of compact groups by Hermann Weyl (1885-1955) and his doctoral student Fritz Peter (1899-1949) in 1927 showing within their basic theory that every compact group is a pro-Lie group;

(ii) the discovery that every locally compact group has a (left) invariant measure by Alfréd Haar (1885-1933) in 1932;

(iii) the discovery in 1934 of the duality between the category of (discrete) abelian groups and the category of compact abelian groups by Lev Semyonovich Pontryagin (1908-1988), generalized in 1935 to the self-duality of locally compact abelian groups by Egbert van Kampen (1908-1942), and by André Weil (1906-1998) in 1938, who also established that a complete topological group with a Haar measure has to be locally compact; (See^[9][19]).

(iv) the enormously influential contribution to the structure of locally compact groups in 1949 by Kenkichi Iwasawa (1917-1998) (see^[22]); 

(v) the positive solution of Hilbert's Fifth Problem, given in 1952 (indeed 9 years after the death of Hilbert) by Andrew Mattei Gleason (1921-2008), Deane Mongomery (1909 -1992), and Leo Zippin (1905-1995); and

(vi) the proof in 1953 by Hidehiko Yamabe (1923-1960) that every almost connected locally compact group is a pro-Lie group.

The research of the structure and representation theories of Lie groups and locally compact groups and their combination in the second half of the 20th century was supported by the preceding rapid development of functional analysis and harmonic analysis. The classes of compact and of commutative groups serve as distinguished samples of research. The appearance of weighty monographs and textbooks exemplify the trend. Here are some of the authors: A. Weil, 1941,^[31], N. Bourbaki, 1940-1982^[3], C. Chevalley, 1946^[5], E. Hewitt and K. A. Ross I and II}, 1963 and 1970^[11], G. P. Hochschild, 1965^[14], S. A. Morris, 1977^[26], D. L. Armacost, 1981^[1], J. Hilgert, K. H. Hofmann, and J. D. Lawson, 1989^[13], K. H. Hofmann and S. A. Morris, 1998 ^[19]. Such a sample continues into the 21st century:

M. Stroppel, 2006 ^[29],

K. H. Hofmann and S. A. Morris, 2006^[18],

K. H. Hofmann and S. A. Morris, 2007^[19],

J. Hilgert and K.-H. Neeb, 2012^[12],

K. H. Hofmann and S. A. Morris, 2013^[19],

E. Kaniuth and K. F. Taylor, 2013^[24],

Y. Cornulier and P. de la Harpe, 2016 [6],

C. Jacoby and P. Loth, 2019^[23]

K. H. Hofmann and S. A. Morris, 2020^[19].

During the development of abstract algebra and Galois theory in the 20th century, the development of profinite groups, i.e., compact totally disconnected groups, in some sense opposite to Lie theory, experienced substantial development (cf. ^[27]). For a p-adic Lie theory see P. Schneider, 2020, ^[28]. Important steps in a general structure theory of not necessarily compact locally compact totally disconnected groups were taken in the 1990s by G.A. Willis innovating the theory by introducing concepts such as tidy subgroups and scaling functions. See^[33][34].

3. The 21st century

After the turn of the millenium the Lie theory turned from Lie groups proper to pro-Lie groups and so from the incomplete category of locally compact groups to the complete category of pro-Lie groups. Meanwhile the concepts of a Lie group had been extended to work for locally convex topological vector spaces yielding locally the underlying spaces of a Lie group. The natural question for the precise overlap of Lie groups and pro-Lie groups then was answered in 2009 by Hofmann and Neeb in a purely topological spirit: A pro-Lie group G is a Lie group if an only it it is locally contractible^[17].

The global structure of almost connected pro-Lie groups was settled by Hofmann and Morris in 2011: Let G be an almost connected pro-Lie group. Then every compact subgroup is contained in a maximal one and all of these are conjugate. There is a closed subspace homeomorphic to a weakly complete vector space E in G such that for each maximal compact subgroup C the function 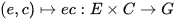is a homeomorphism ^[20]. It follows from results on compact groups that the topological nature of an almost connected pro-Lie group is completely known: Any infinite almost connected pro-Lie group is homeomorphic to a pro-Lie group of the form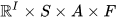

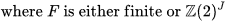
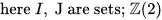
is the two-element group, where S is a compact connected group that agrees with its commutator subgroup S' and is, modulo a central profinite subgroup, a cartesian product of compact connected simple Lie groups, and where, finally, A is a compact connected abelian group. ^[21]

The Lie algebras of pro-Lie groups are profinite dimensional in the sense that they are projective limits of finite dimensional Lie algebras. In the background is the even simpler idea of (real) profinite dimensional vector spaces. It emerged (e.g. in^[19] in 1998) that a vector space is profinite dimensional iff it is the dual of a real vector space with the topology of pointwise convergence iff it is isomorphic as a topological vector space of the form

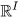
(with the Tychonov topology for some set I) iff it is the Pontryagin dual of a real vector space with its finest locally convex vector space topology. (Cf.^[19], Appendix 7). Such topological vector spaces became known as being weakly complete. In particular, the Lie algebra of any pro-Lie group is weakly complete and so is,by Yamabe's Theorem, the Lie algebra of any locally compact group. It turned out to be useful to note that the categories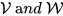

of real vector spaces, respectively, weakly complete vector spaces, are dual.

In this context it is natural to describe the associative multiplication of a weakly complete real algebra A with identity as a continuous linear map, or morphism

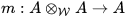
with appropriate properties. The duality between

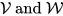
describes this situation by an appropriate linear map

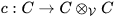
with the dual C of A. Since the middle of the last century such an algebraic object (C,c) became known as a coalgebra. Pure linear algebra showed that such a coalgebra always is the ascending union of the finite dimensional vector subspaces C_j such that

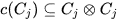
(Cartier's Lemma; cf. ^[25].) Duality now yields to the following remarkable result (where “algebra” means “associative algebra with identity”: Every real weakly complete topological algebra A is profinite dimensional, that is, is a projective limit of finite dimensional quotient algebras A/I modulo closed two-sided ideals I. (See ^[2].) The multiplicative group L of invertible elements is a dense subset of A. As a consequence of the result above, L is the projective limit of the finite dimensional quotients 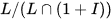and so is an almost connected pro-Lie group. Its Lie algebra is A_Lie , the weakly complete vector space underlying A with Lie bracket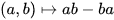

and its exponential function is the exponential function of A defined by the exponential series converging everywhere. A weakly complete symmetric Hopf algebra A is only a step away from a weakly complete algebra: It has a continuous comultiplication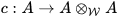

a continuous coidentity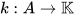

and a continuous symmetry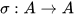

(see^[19], Definition A3.93 on p.856). The elements     

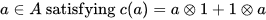satisfying are called primitive and those satisfying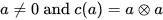

grouplike. The connection with Lie theory is evident through the following fact: The set 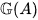of grouplike elements of a weakly complete symmetric Hopf algebra A is a pro-Lie group contained in L. The set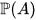

of primitive elements is a pro-finite dimensional Lie subalgebra of A_Lie. Finally,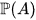

is the Lie algebra of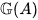

whose exponential function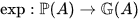

is induced by the exponential function of A. (See^[2][7][9].)

4. Lie theory and algebras

The emergence of weakly complete algebras and Hopf algebras transformed pro-Lie group theory. This is seen, firstly, by the theory of weakly complete group algebras of pro-Lie groups, notably, compact groups (cf. ^[7][15][19]) and, secondly, the foundations of weakly complete universal enveloping algebras of profinite dimensional Lie groups (cf. ^[15][16]). The weakly complete group algebra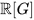

of a pro-Lie group G is in fact a weakly complete symmetric Hopf algebra containing a copy of G as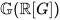

and a copy of its Lie algebra as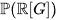

 For a compact group G, the algebra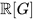

is a product of finite dimensional minimal ideals whose structure one knows in detail (cf. ^[19], Chapter 3). If, in a weakly complete symmetric real Hopf algebra A, the subset of grouplike elements (see ^[19], Definition A3.95, p.857) is compact, and if its linear span is dense in A, then we call A compactlike. Now one has the following fundamental equivalence theorem: For a compact group G, the weakly complete group algebra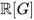

is compactlike and all compactlike weakly complete symmetric Hopf algebras are so obtained. That is, the two categories of compact groups and that of compactlike weakly complete symmetric Hopf algebras are equivalent. The duality of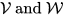

establishes a duality precisely between the categories of real symmetric Hopf algebras and of weakly complete symmetric Hopf algebras. If we call a symmetric Hopf algebra reduced provided that its weakly complete dual is compactlike, we obtain the following  duality theorem: The category of compact groups is dual to the category of real reduced symmetric Hopf algebras. This is the Duality Theorem of Tannaka,1939, (see^[30]) and  Hochschild, 1965, (see ^[14]) in contemporary formulation.

The weakly complete universal enveloping algebra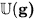

of a profinite-dimensional Lie algebra g over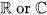

is a weakly complete symmetric Hopf algebra containing g in the Lie algebra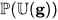

of its primitive elements, and it is characterized by the following universal property: Every continuous Lie algebra morphism g → A_Lie  for a  weakly complete algebra A extends uniquely to a continuous morphism of weakly complete algebras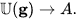

It contains a dense copy of the classical universal enveloping algebra generated by g. The universal enveloping algebra of a profinite-dimensional Lie algebra g stands for what is traditionally known by “Lie's Third Fundamental Theorem” known as the slogan “each Lie algebra is the Lie algebra of some group”. Indeed in the current context we have: For any real profinite-dimensional Lie algebra g, its universal enveloping algebra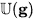  

contains in its group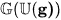

of grouplike elements a pro-Lie group G having g as its Lie algebra, such that its exponential function g → G is induced by the exponential function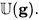 

( See ^[16].）

This entry is adapted from the peer-reviewed paper 10.3390/axioms10030190