Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Biomedical
Reverse total shoulder arthroplasty (RTSA) is an established treatment for elderly patients with irreparable rotator cuff tears, complex proximal humerus fractures, and revision arthroplasty. Computational modeling has been used to investigate the effects of implant design, intraoperative component placement, and surgical technique on postoperative shoulder biomechanics after RTSA, with the findings ultimately used to elucidate and mitigate complications.
- reverse shoulder prosthesis
- finite element model
- biomechanical model
- rigid body model
1. Introduction
Reverse total shoulder arthroplasty (RTSA) has traditionally been used in the treatment of patients with a rotator cuff-deficient arthritic shoulder. However, over recent years, indications for RTSA have expanded to include irreparable rotator cuff tears, complex proximal humerus fractures in elderly patients, severe glenoid bone loss, revision arthroplasty, and tumour resection. In the United States, the number of primary RTSAs has almost tripled from 2012 to 2017, accounting for around 60% of all total shoulder arthroplasty procedures in 2017 [1]. In Australia, over 80% of total shoulder arthroplasty procedures performed in 2019 were RTSA [2].
RTSA, originally designed by Professor Paul Grammont in 1985, reverses the ball-and-socket anatomy of the anatomical glenohumeral joint [3]. This has the effect of medialising the centre of rotation of the glenohumeral joint, thereby increasing the moment arms (leverage) of the deltoid and facilitating the recruitment of more of its fibres during elevation [4,5,6]. The semi-constrained joint articulation confers stability, compensating for absence of rotator cuff muscles to a degree, while the prosthesis design also distalizes the humerus which tensions the deltoid, ultimately allowing for increased force generation and range of joint motion [7].
Despite the biomechanical benefits and widespread use of RTSA, complication rates remain a concern [8,9,10,11,12,13,14,15,16]. A recent study of 4124 shoulders with RTSA reported a complication rate of 16.1% [17]. Shoulder instability, periprosthetic fracture, infection, and component loosening are the leading causes of revision RTSA [17,18]. Scapular notching, acromial fractures, instability, and component loosening are a consequence of post-operative joint biomechanics and can be directly attributed to implant design and placement. The need for a deeper understanding of muscle and joint function after RTSA, to inform strategies to mitigate complication, has motivated the development of more sophisticated computational models of RTSA.
2. Computational Modeling Techniques
Computational modeling of RTSA facilitates estimation of muscle and joint loading, which is currently impossible to measure non-invasively in vivo. Modeling and simulation of RTSA has played a critical role in guiding implant positioning and surgical technique [19,20,21,22], prosthesis selection [23,24], implant design [25,26], and post-operative rehabilitation prescription [27,28]. To date, most modeling and simulation tools require high levels of expertise and are generally restricted to the research setting.
Biomechanical computer models are broadly categorized into three groups: rigid body models, finite element (FE) models, and multi-body models. Rigid body models characterize bones as non-deformable segments. Through simulating joint kinematics and internal and external forces, these models are used to investigate changes in muscle and joint function after RTSA [29,30]. The primary advantage of rigid body models is that they can run quickly and at a low computational cost. For example, shoulder muscle forces during upper limb elevation can be calculated in several minutes using a subject-specific rigid body model (Figure 1A) [28,31]; however, since deformation mechanics is neglected, the internal stresses and strains in the bone and implant cannot be accurately evaluated using this method. An important utility of rigid body models has been in their capacity to estimate the influence of arthroplasty on muscle moment arms, muscle and joint forces, and range of motion (ROM) at the shoulder, which are primary indicators of implant functional performance [21,23,24,29,30,31,32,33,34,35,36,37,38,39,40].
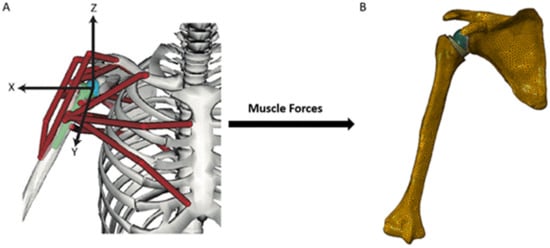
Figure 1. A multi-body modeling framework used to investigate joint stability after RTSA [28], including a rigid body model to simulate muscle and joint loading at the shoulder (A), and a FE model to calculate internal stresses and strains at the bone and implant (B). The muscle and joint forces calculated from the rigid body model were input into the finite element model and used to drive simulations of joint loading during activities of daily living.
In contrast, FE models provide estimates of material deformation by discretization of structures into a finite number of elements, each element of which can be interrogated for load response such as stress, strain and displacement. This may reveal, for instance, how joint load is transmitted to bone via joint contact loading. The FE method has been used to investigate wear, component fixation, and joint stability after RTSA [41,42,43,44,45], which has aided in implant selection, intraoperative positioning, and fixation [20,44,46,47]. However, in contrast to rigid body models, FE model simulations can be computationally expensive. A FE model of the shoulder after RTSA, containing around half a million elements (Figure 1B), takes more than thirty minutes to run using a standard desktop computer [28].
Finally, multi-body musculoskeletal models input muscle and/or joint reaction force estimations from a secondary model simulation, typically derived from a rigid body model, into a FE analysis. This approach provides a basis for muscle and joint force prediction, as well as bone and implant deformation. Multi-body modeling has been used to assess the performances of different implant designs and surgical techniques in RTSA, with the capability to take into account accurate and physiologically meaningful boundary conditions [28,48,49,50,51].
This entry is adapted from the peer-reviewed paper 10.3390/jcm10225336
This entry is offline, you can click here to edit this entry!
