Ejectors: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Agricultural Engineering
Contributor:
Linh Ve

Ejectors are broadly of two types based on geometric construction, constant area mixing (CAM) and constant pressure mixing (CPM). Eamesproposed a new design with constant rate of momentum change, which has the advantage of both CAM and CPM. Computational and experimental studies show better overall performance of ejectors with increases in critical condensing temperatures and higher entrainment ratios.

  • ejector
  • design modification
  • sustainable design

1. Ejectors

1.1. Construction

A general ejector is constituted of the inlet pipe, nozzle, suction chamber, mixing chamber, throat and diffuser (Figure 1). Motive and suction fluid of the same or different phases flow through the inlet and suction port, mix in the mixing chamber, accelerate through the nozzle and recover pressure in the diffuser. Primary nozzles are usually of converging/diverging type (based on application). Carbon steel, stainless steel, brass, titanium, PTFE, carbon, poly propylene, UPVC, AB and Hastelloy are common materials used for their construction [1].
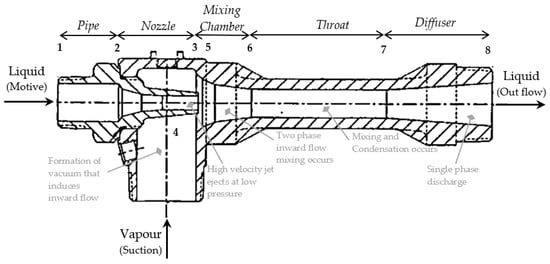
Fluids 06 00409 g002 550
Figure 1. Components in simple ejectors.

1.2. Applications

Operationally, ejectors can be single phase or multiphase systems with compressible or incompressible flow functioning as pump, compressor, heat exchanger, vacuum pump or condenser. Depending on the application, the primary fluid can be liquid, or gas and the secondary fluid can be liquid, gas or particles. Broadly, they are categorized as liquid–liquid, liquid–gas, gas–liquid, gas–gas, liquid–particle and gas–particles ejectors. The application and function of ejectors in several processes has been highlighted below:

1.2.1. Vacuum Pumping and Degassing

The fact of installation flexibility and efficient operation supports ejectors as a suitable alternative for vacuum generation. They are used in vacuum packing, drying, evaporation, gas ejection, etc. processes in industries. [2] There is zero secondary flow, while using ejectors as a vacuum pump. Macia et al. explains the influence of zero secondary flow on unsteady phenomenon in vacuum ejectors. [3] The physics of vacuum generation and formation of recirculation bubbles on circumference of jets has been visually explained by Kumar et al. [4]. In steel industries, larger rejection due to voids and strength led to adaptation of ejector-aided vacuum cooling. After placing of the ladle/mold in the cooling chamber, degassing is performed, which ejects hydrogen, oxygen, nitrogen and other dissolved gases trapped within the mold, ensuring cleanliness, ductility and toughness of the steel. This vacuum is increased at different steps by regulating motive flow [5][6]. A case study from National Forge Company, PA, recommended vacuum degassing through ejector, as an essential step in producing high quality steel. The installed system was not able to meet the vacuum requirement after being in operation for thirty-six years, pumping hot and dirty gases from steel at a temperature of around 3000 °F. The new system was developed with SS 303 material and ensured periodic cleaning of scales [7].

1.2.2. Power Cycle

Although the operational limit of gas turbines is 1200 °C, cost, life and ash deposition limit the maximum steam temperature to 560 °C. The physical structure allows high temperature operation for better efficiency of Rankine cycle but the high steam pressure and resultant dynamic effect on blades limits the range. A topping cycle allows operation of high temperature boilers at low pressures by using very low vapor pressure top fluid, but they require high temperature turbines. [8] With an ejector-based topping cycle, they compress secondary gas which prevents loss of exergy through secondary work [9]. Oliveira et al. [10] developed a combined power generation and cooling cycle in ejector-based Rankine cycles. A part of turbine power output was utilized in running ejector-based cooling systems. The performance of these combined systems was also evaluated by Zhang et al. and Zhang et al. [11][12].

1.2.3. Other Applications

Desalination: is the major application objective of this work. The prospective application of ejectors in desalination systems for combined vacuum pumping and condensation with active vapor transport has been examined in the later section.
Pump priming: This is essential to minimize start-up damage on the impeller by reducing the gas boundary. Ejectors have been a compulsory part for priming of self-non-priming industrial centrifugal pumps [13]. Liquid/compressed air as motive fluid creates a vacuum inside the suction line of the pump, which draws the liquid to submerse the impeller (Figure 2). Vacuum pumps either require liquid supply or limit liquid injection during dry operation, hence ejectors stand out as superior (compared to vacuum pump, priming tank and foot valves). They were found to be installed in any orientation and recorded to be effective in priming up to 8 m suction head with primary fluid pressure of 4–10 bar [14]. The flexibility on adjustment of vacuum level and priming speed though primary flow and simple construction and installation makes it more favorable [15][16][17][18].
Refrigeration: The requirement of low capital and operational cost, low energy and simplicity has suggested ejector refrigeration systems as a strong alternative to mechanical compressor-based systems [19][20]. Details on the application in refrigeration technology has been reviewed by several reviewers in the past [21][22].
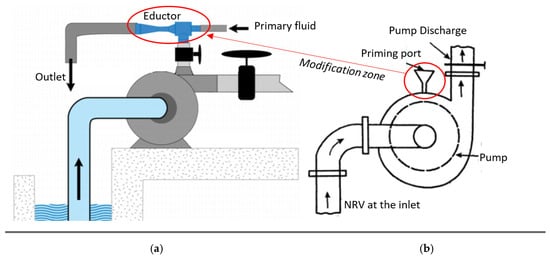
Fluids 06 00409 g003 550
Figure 2. (a) Ejector priming, (b) manual priming (source [23]).
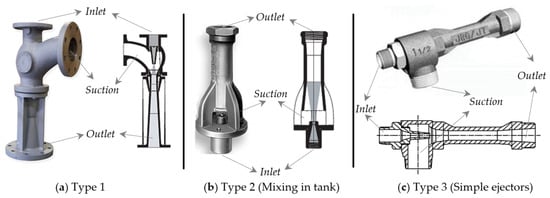
Based on the application in the industrial technologies various ejectors are available in the market. The construction and shapes of ejectors are shown in Figure 3.
Fluids 06 00409 g004 550
Figure 3. Commercial products available on the market [24][25][26][27][28][29].

1.3. Operational Principle

In the case of ejectors, the jet passing nozzle induces steady flow eddy current to its surroundings, at the suction chamber, due to momentum transfer, which accelerates the secondary flow. During this momentum exchange of primary fluid into secondary, the secondary phase forms dispersed bubbles inside the primary flow stream. This momentum exchange is defined by the momentum exchange coefficient which is a function of drag coefficient, bubble size and phase velocities [30]. The potential energy in two phases is converted to kinetic energy through a special case of Bernoulli—Venturi effect, where flow mixes and accelerates through the mixing chamber. The two-phase mixing results in the induction of pressure shock waves of high frequencies. The accelerated flow with dropped static pressure passes through the throat; this causes further movement of the secondary phase from the suction port into the motive stream. At the diffuser section, velocity decreases and hence the fluid recovers pressure energy and compress the secondary phase before discharge. Thus far, the system has been able to recover only about 40% of pressure energy. Here, the system is performing three operations at once, causing suction of low-pressure fluid, mixing it with mainstream and discharging at a higher pressure. The discharge occurs at an intermediate of motive and suction pressure [31][32].
The static pressure difference in the two-phase flow through a narrow constriction, may result in fan out of primary flow core and form a fictive throat, where flow continues after the secondary flow attains sonic condition. Although not practiced, but concepts on the use of additional suction nozzle for pre-acceleration of stagnant suction fluid has been discussed to reduce large shearing loss during mixing of phases at the high-velocity difference. It can also be a supporting factor to minimize the fan out phenomenon. Performance characteristics of ejectors are defined through suction pressure ratio and mass entrainment ratio. The ratio of system exits to suction flow pressure is suction pressure ratio and the ratio of suction to motive mass flow rate is entrainment ratio. A system is said to be well designed if it has large suction pressure and mass entrainment ratios at the same time [33].

1.4. Performance Estimation Parameters

For almost all applications, performance is measured through entrainment ratio (ER) and compression ratio (CR). Compression ratio is the fraction of delivery pressure to suction pressure and entrainment ratio is a fraction of suction mass to motive mass flow rate, numerically defined by equations.˙m
dP
Calculated values of ER for each of the cases of CR are plotted for Figure 4, which forms performance characteristics for the ejector. There are two operational conditions, stable and unstable. With momentum induction of motive flow, secondary flow continuously entrains, resulting in declination of secondary flow pressure, this causes a gradual increment in CR of the ejector. Figure 3 describes three prime operation modes, stable, critical and unstable. At stable, the entrainment ratio remains unchanged until its critical CR is reached. At critical CR, the highest suction occurs, hence it is called maximum discharge point (MDP). Post this, fluctuation and drop in entrainment ratio were observed along with reversed flow. Reversed flow condition is the minimum ER above which motive flow reverses in the loop. Practically, the performance curve is drawn by varying back pressure, at constant inlet pressure and temperature [34].
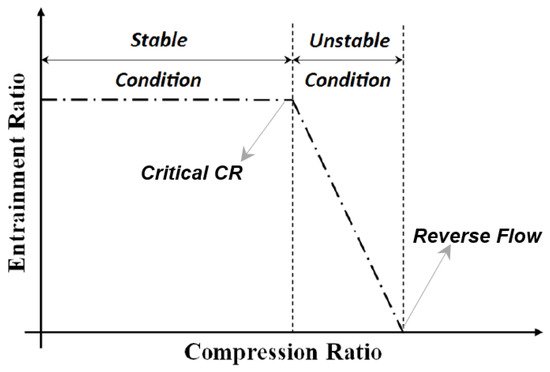
Fluids 06 00409 g005 550
Figure 4. Ejector performance curve.
Experimental methods with implementation of pressure and flow sensors or orifices have been used to log the result for performance estimation. Computational methods with pressures as boundary conditions were found to be abundantly implemented, along with an additional definition of condensation model in some of the cases.

2. Design Modifications of Ejector

Ejectors are broadly of two types based on geometric construction, constant area mixing (CAM) and constant pressure mixing (CPM). Eames [35] proposed a new design with constant rate of momentum change, which has the advantage of both CAM and CPM. Computational and experimental studies show better overall performance of ejectors [36] with increases in critical condensing temperatures and higher entrainment ratios. Kumar et al. [37] considered the rate of energy change as a primary consideration for ejector design. The constant rate of kinetic energy change method allows overcoming the thermodynamic shock by shifting to a description of flow physics.

2.1. Nozzle

Ariafar et al. [38] numerically studied the effect of three different nozzle geometries (throat diameter ranging from 10.2 to 12 mm) on the performance of the thermo compressor, using water vapor as motive fluid with pressure ranging from 1.25 to 1.75 bar. With larger nozzle diameter, higher mass flow rate occurs resulting in higher momentum and kinetic energy hence it results in the formation of high critical back pressure at the system outlet. This in turn has been found to decrease the entrainment ratio (Figure 5).
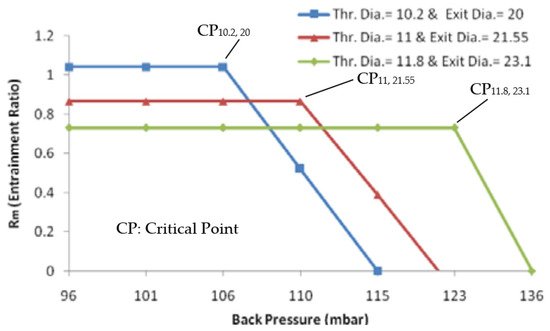
Fluids 06 00409 g006 550
Figure 5. Entrainment ratio vs. back pressure for the ejector (source [38]).
Behtash et al. [39] discussed the effect of different primary flow geometries (two circular nozzles of diameter 15 and 30 mm, two elliptical nozzles with minor and major axis ratios of 0.4 and 0.6 with b = 30 mm, a square nozzle with length 30 mm and two exits) on the interaction of diffracted shock wave patterns and resulting vortex loop emissions.
Sharifi et al. [40] numerically optimized and verified the performance of a malfunctioning steam jet ejector, for its compression ratio, as the designed primary pressure was 6 bar while its operational requirement of vacuum was achieved when raised to 8 bar. Focusing its application for the MED desalination process for maintaining low pressure inside the evaporator, the study was performed on ten different nozzle geometries for highest entrainment at constant boundary condition. Figure 6 is the result of numerical simulation for the designed pressure of 6 bar and operating pressure of 8 bar. Compared to operating pressure, the designed pressure condition has higher entrainment ratio as the motive mass flow through choked nozzle is higher, while maximum discharge point (MDP) is higher with operating pressure because of larger compression ratio caused by high energy motive steam at high pressure entering the system. Optimization may be affected by several methods but one of the important factors is improving geometries. For technical and financial feasibility, with a goal of attaining desired vacuum level at suction chamber at nominal operating condition of 6 bar, optimization was performed. A nozzle has major dimension parameters, namely, converging and diverging length, inlet, outlet and throat diameters. Higher ER refers to higher suction flow, the 9th profile in the observation shows the highest ER of 0.155 with CR of 5.27.
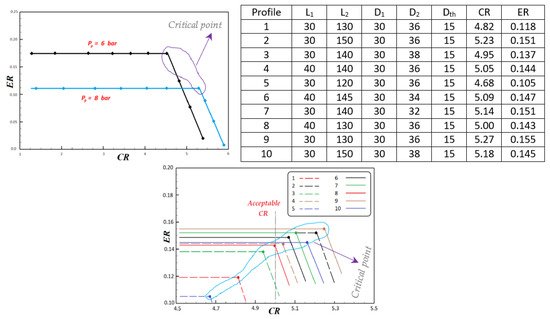
Fluids 06 00409 g007 550
Figure 6. Performance curve of an ejector for designed and operating pressures, 6 bar and 8 bar (source [40]).
Sag et al. [41] experimentally studied the effect of throat diameter and position of primary nozzle on performance of the vapor compression system, with design and manufacturing of ejectors based on established mathematical relations. The system operates on motive fluid such as R134a, causing entrains from the evaporator. Primary nozzles have diameters of 12 mm and angles of 36°, with primary nozzle throat diameters of 2.1, 2.2, 2.4 and 2.5 mm, having constant section throat and mixing chamber of 9 mm. Figure 7 shows entrainment ratios at different motive nozzle throat diameters; at 2.3 mm, the maximum entrainment ratio was observed since the ratio of missing chamber cross-section to cross-sectional area of nozzle throat is optimum. The variation of around 4% with geometry was observed.
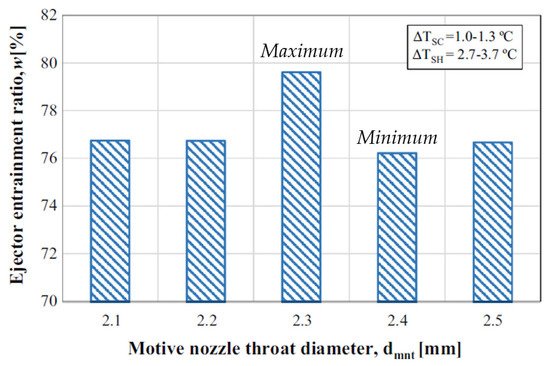
Fluids 06 00409 g008 550
Figure 7. Effect of primary nozzle throat diameter on entrainment ratio [41].
Xue et al. [42] used a computational method to study the effect of three nozzles (conical, petalage and crenation nozzles) on performance of supersonic ejectors. Except for outlet shape, all other parameters are kept constant (area ratio, area of throat of mixing chamber to nozzle throat = 3.24, primary throat diameter = 10 mm, length of ejector’s throat is 6 times its diameter; 18 mm, with constant, exiting area). The study focused on critical, sub-critical and back flow operational modes where both back pressure and entrainment ratio were examined to explore the highest back pressure and entrainment ratios. Figure 8 is the plot for entrainment ratio versus back pressure, computed from the numerical study; at initial conditions, entrainment ratio is higher for crenation while at critical back pressure, petalage has highest entrainment as well as back pressure.
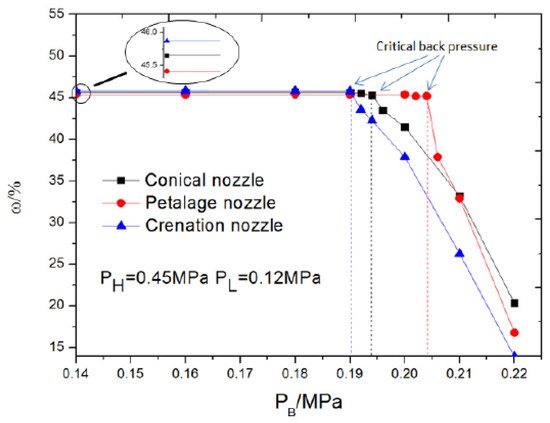
Fluids 06 00409 g009 550
Figure 8. Entrainment ratio vs. back pressure for different nozzle geometries [42].
Elhub et al. [43] studied the optimum position of nozzle exit for cooling cycle in R134a refrigeration systems, through computational method. An extended work is presented with a provision for a movable ejector at varying distance from 2 to 8 mm, to accommodate varying operational requirements and conditions. At low distance, improper mixing between primary and secondary flow resulted in low entrainment, while at higher distance, outlet pressure is found to be more dominant in causing back pressure, hence 3 mm is the optimum distance at which entrainment ratio of about 0.7 was achieved.
Seckin [44] used an empirical method to study the effect of constant pressure two-phase ejector primary nozzle throat diameter, on the ejector expansion refrigeration cycle using R134a as the refrigerant. At condenser temperatures of 50, 60 and 70 °C and evaporator temperatures of 0 °C, nozzle throat diameter, condenser temperature and entrainment ratio are affected. With increasing temperature of condenser, larger diameter nozzles are required.
Xu et al. [45] performed experimental investigation on supersonic (converging-diverging with throat diameter of 1.3 mm and exist diameter of 1.36 mm) and subsonic (converging with throat diameter of 1.3 mm) nozzle with variable geometry ejector to utilize unstable solar heat as driving energy for stable refrigeration systems. The diameter and length of mixing sections are 2.08 and 10.0 mm, respectively. Driving and suction flow are induced through generator and evaporator, respectively, using R134a as working fluid. Variable geometry ejectors were found to have achieved better performance in varying operating conditions and supersonic nozzles were found to demonstrate better performance compared to subsonic nozzles. Figure 9 shows the performance of ejectors for varying nozzle openings for two different nozzle geometries, where optimum point for best performance was observed, which decreases on both sides.
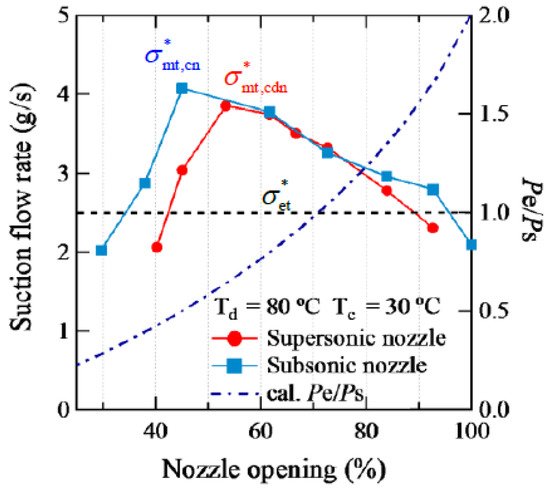
Fluids 06 00409 g010 550
Figure 9. Performance with different nozzle structure at condensing temperature of 30 °C [45].

2.2. Primary Nozzle Position

Conventional ejectors are designed to operate at a single optimum point; in practice operation may vary from it, which results in performance deterioration. Nozzle optimum position is to be set such that no secondary flow occurs.
In the mixing section, motive and suction fluid mixes in the phenomena of heat and mass transfer, during pressure recovery of this flow shock waves are induced in the diffuser. Zhang et al. [46] computationally studied the effect of varying primary nozzle openings on ejector operation. Pressure of 300 kPa, 80 kPa and 220 kPa were selected for motive inlet, suction and outlet, with water vapor as motive fluid. Results based on turbulence models k-e standard, k-e RNG and k-e RSM, were compared with experiments and were compared with experimental conditions. Performance deterioration with exceeding discharge pressure beyond critical pressure was observed, where computational results with k-e RSM, were in better agreement with experiments. A difference in entrainment ratio of 0.1 was observed, which is around a 47% improvement.
Dong et al. [47] used movable primary nozzles of three kinds and diffusers of two kinds for identifying its optimum position and design, respectively, experimentally in the refrigeration cycle (described in Figure 10). Variation in optimum operational position was observed in all the cases with better coefficient of performance for nozzle 1, location of position optimum position is dependent on the kind of nozzle being used and it is independent of the type of diffuser being used.
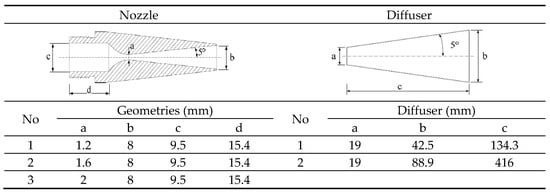
Fluids 06 00409 g012 550
Figure 10. Geometry considered for this study [47].
Mani et al. [48] used UDF function to define oscillation between two points, for computational analysis of oscillating primary nozzle. Figure 11a,b is the velocity contour plot for oscillation at 5 Hz frequency at 2° and 10° angles, with inlet, suction and outlet pressure boundary conditions as 4.5 bar, 1 bar and 1 bar respectively. It shows that velocity waves transport along with the axial plane of the system. Figure 11c is the plot for varying frequency at different oscillation angles. In observed cases, ER is lower compared to the steady result, but comparing absolute oscillating ranges, it shows improvement in results with increasing oscillation angle; R&D can focus on discovering a suitable combination of amplitude and frequency to enhances performance. There are challenges in integration of actuator for consistency in oscillation in the technology.
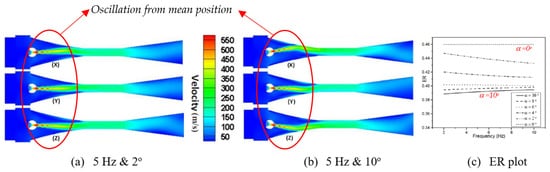
Fluids 06 00409 g013 550
Figure 11. (a,b) Velocity contours at different oscillation angles with 5 Hz frequency (c) ER plot at different frequency and oscillation angles (source [48]).

2.3. Inlet Swirling Vanes

Performance of the ejector system can be enhanced by proper mixing of motive and suction flow. Improvement in entrainment ratio by inducing swirl in primary flow has been studied [49], it has been highlighted to have increased contact time between primary and secondary flow with increased shear force effect.
Yan et al. [50] studied the effect of swirling vanes (for both steam and water) on injectors with central water jets (Figure 12). Two swirling water vanes were present at the beginning of nozzle throat while eight steam swirling vanes were present, which caused disturbance in the velocity field inducing vortexes when flow passes through it. Observations for entrainment ratio and resistance coefficient were performed for an inlet pressure of steam and water and temperature. Water swirling vanes were found to be efficient in improving entrainment ratios, exergy and resistance coefficients, while steam swirling vanes caused degradation in performance.
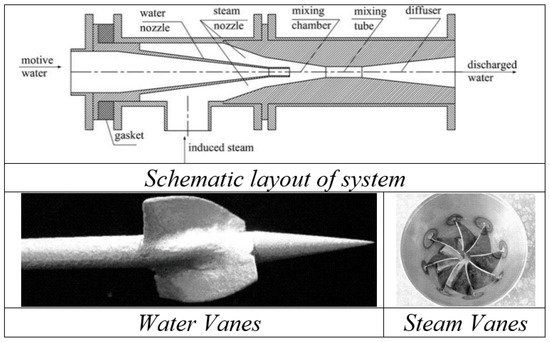
Fluids 06 00409 g014 550
Figure 12. Schematic test setup with swirling vanes for water and stem nozzle [50].
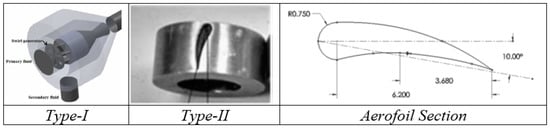
Banu et al. [51] focused on an air ejector system to analyze the influence of swirl for prospective application in vapor jet refrigeration. A three-dimensional numerical approach basis, with and without swirl, has been studied and verified through PIV technique. Figure 13 depicts the aerofoil cross-sectioned swirl generators, type-I and type-II, implemented in the system, placed at convergent section upstream. For geometry with primary nozzle diameter and area ratio of 3.2 mm and 2.56, an air compressor system with 100 L reserve was used in a transparent system. Primary flow measurement was performed through rotameter while secondary is measured with an orifice meter. With an increase in radial velocity compared to no swirl, there has been an enhancement of performance by 5% [52], 2% and <2% for cases with type-I, type-II with 5 vanes and type-II with 3 vanes.
Fluids 06 00409 g015 550
Figure 13. Swirl generator of Banu et al. [51][52].
Banu et al. [53], performed 3D numerical simulations for a different arrangements of type-I swirl generators with sweep angles of 10°, 20° and 30°, discussed in [20] along with verification through PIV. The swirling intensity was quantified with the non-dimensional parameter swirl number (SN); a ratio of the axial flux of tangential momentum to axial momentum as defined by the following equation [54].x Uθ r dAR∫R0ρ Ux2 dA
Figure 16 shows a reduction in axial velocity with primary stream pressure due to decreasing static pressure at the throat, causing velocity decay exponentially along the ejector. A sweep of 30° in cavity type swirl generator showed 15% improvement in ER.
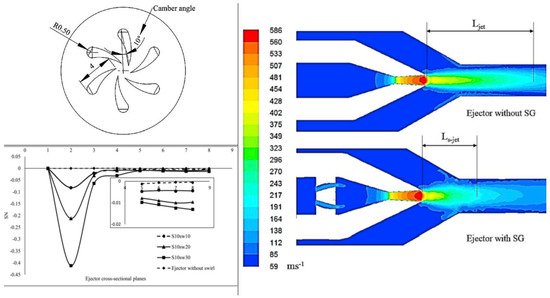
Fluids 06 00409 g016 550
Figure 14. Swirl generator design, its intensity and effect on flow passing jet [53].
Chlappetta et al. [55] created a US patent for swirl vanes in vapor compression refrigeration systems shown in Figure 15. In addition to stationary swirling vanes, free spinning rotors were actively used in exchanging pressure and enhancing mixing. Garris et al. [56] mounted a free-spinning rotor on a fixed spindle (Figure 16). It uses non-steady fluid and supersonic flow principles to obtain compression of induced flow. This reduces losses during turbulent mixing, allowing better adiabatic efficiency during the topping cycle of rankine and gas cycles and refrigeration cycles. Hong et al. [57] updated the research status of this novel design computationally, with various geometrical arrangements; the geometry of rotor vanes was prioritized with leading and trailing edge and cross-sectional shape [58].
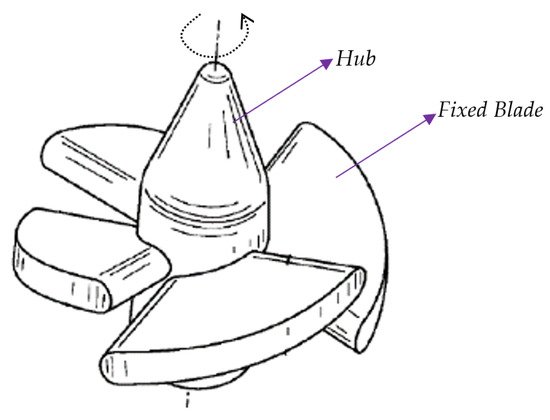
Fluids 06 00409 g017 550
Figure 15. Swirl vanes proposed by Chlappetta et al. [55].
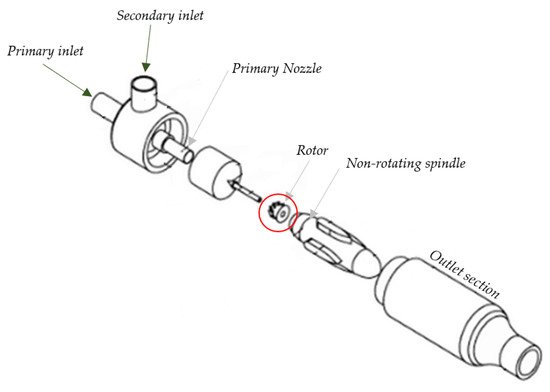
Fluids 06 00409 g018 550
Figure 16. Free spinning pressure exchange device in ejector by Garris et al. [56].

2.4. Throat Sizes

Water is an excellent refrigerant with high latent heat of vaporization, specific heat, suitable heat transfer characteristics, non-corrosive and adoptable by environmental concerns. In refrigeration systems, ejector performance is the deciding factor governing overall coefficient of performance. Ejector efficiency is governed by the entropy generation process, where conventional systems have two major sources: turbulent mixing and strong normal shock waves.
Alhussan et al. [59] varied the throat diameter ratio to investigate the structure of flow induction in an unsteady supersonic fluid with steam as the motive fluid. The pressure exchange ejector showed the mass flow ratio to be near to unit with high-pressure recovery.
In a vapor compression refrigeration cycle, throttling is a significant loss, hence modification through adaption of ejectors ensure optimized performance. Chaiwongsa et al. [60] studied the effect of throat diameter of the motive nozzle (0.8 mm, 0.9 mm and 1 mm) on CoP of a refrigeration systems with R134a for primary and secondary flow. A system with smaller diameter is found to have larger COP.
Bi et al. [61] developed a computational model to study the effect of throat diameter. Their results showed no significant change in the entrainment ratio location of diamond shock (abrupt standing shock wave variation) (Figure 17). Increasing length increased friction resistance, which eventually increased the critical back pressure up to its maximum value of operation and then decreases. For operational conditions, there is always an optimum point, and in this case, it was 550 mm.
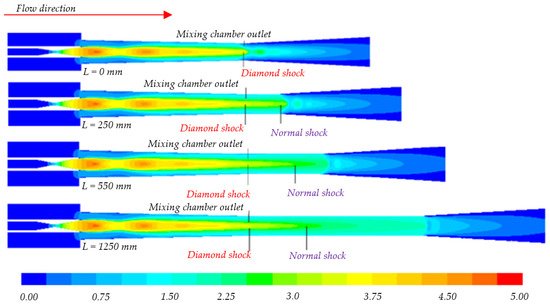
Fluids 06 00409 g019 550
Figure 17. Mach number contour for varying throat length [61].
Saini et al. [62] experimentally studied vacuum pressure for three throat lengths (10 cm, 20 cm and 30 cm) with constant throat diameter of 2 cm. Suction capacity was examined based on the absorbed weight of saw dust from the suction port. At 30 cm, a minimum pressure of 87.5 kPa and maximum suction of saw dust 32.2 grams were measured, as compressive strength at the top of the ejector will be converted to flow velocity with longer length.
Ren et al. [63] used a two-throat nozzle ejector in a TPERC (two-phase ejector refrigeration cycle) system and experimentally observed the consequent entrainment ratio using R134a refrigerant. Figure 18 provides the geometric description for de Laval and two throat nozzles, in both cases entrainment ratio was increased with cross-sectional area, but the value was larger (i.e., 0.375) for the two-throat system.
Fluids 06 00409 g020 550
Figure 18. Schematic diagram of two-throat nozzle ejector with throat CSA (mm2) [63].

This entry is adapted from the peer-reviewed paper 10.3390/fluids6110409

References

  1. Berkeley, F.D. Ejectors; Graham Manufactring Company Inc.: Batavia, IL, USA, 1958; Available online: https://www.graham-mfg.com/usr/pdf/TechLibVacuum/25.PDF (accessed on 1 June 2019).
  2. Shaozhi, Z.; Luo, J.; Wang, Q.; Chen, G. Step utilization of energy with ejector in a heat driven freeze dring system. Energy 2018, 164, 734–744.
  3. Macia, L.; Castilla, R.; Gámez, P.J. Simulation of ejector for vacuum generation. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 659, pp. 1–7.
  4. Kumar, R.A.; Rajesh, G. Physics of vacuum generation in zero-secondary flow ejectors. Phys. Fluids 2018, 30, 066102.
  5. Knight, J.; Met, M. The use of steam Ejectors for the Vacuum Degassing of steel. Proc. Inst. Mech. Eng. 1966, 181, 225–241.
  6. Kuznetsov, V.A.; Kats, Y.L. Economical vacuum degassing of steel with the use of mechanical pumps. Metallurgist 2007, 51, 220–225.
  7. Winter, R.D.; Caldwell, J.E. Vacuum Degassing with Ejector Technology; National Forge Company: Irivne, CA, USA, 1997.
  8. Freedman, B.Z.; Lior, N. A Novel High-Temperature Ejector-Topping Power Cycle. J. Eng. Gas Turbines Power 1994, 116, 1–7.
  9. Garris, C.A. Pressure Exchange Ejector. USA Patent US7497666B2, 20 September 2005.
  10. Oliveira, A.; Afonso, C.; Matos, J.; Riffat, S.; Nguyen, M.; Doherty, P. A combined heat and power system for buildings driven by solar energy and gas. Appl. Therm. Eng. 2002, 22, 587–593.
  11. Zhang, C.; Lin, J.; Tan, Y. A theoretical study on a novel combined organic Rankine cycle and ejector heat pump. Energy 2019, 176, 81–90.
  12. Zhang, K.; Chen, X.; Markides, C.N.; Yang, Y.; Shen, S. Evaluation of ejector performacne for an organic Rankine cycle combined power and cooling system. Appl. Energy 2016, 184, 404–412.
  13. The Process Piping. Introduction to Priming in Pumps, The Process Piping. 2020. Available online: https://www.theprocesspiping.com/introduction-to-priming-in-pumps/ (accessed on 17 October 2020).
  14. Sulzer. Sulzer Ejector for Priming. 2020. Available online: https://www.sulzer.com/china/-/media/files/products/pumps-accessories/pump-and-lifiting-station-accessories/brochures/ejectorforpriming_e10514.ashx?la=en (accessed on 17 October 2020).
  15. Techmon. Variator Priming Ejector–VG. 2020. Available online: https://www.techmon.eu/products/varitor-priming-ejector-vg/ (accessed on 7 July 2020).
  16. Iron Pump. P-type Ejectors—Dimensions & Weights. 2020. Available online: https://ironpump.com/images/Products/Ejector-P-Type-Data-Sheet.pdf (accessed on 17 October 2020).
  17. G.A. Hanrahan Pty. Ltd. Ejector for Steam or Air Operation. 2020. Available online: http://www.hanrahanengineering.com.au/brown-ejector/ (accessed on 17 October 2020).
  18. Prime Tech Ejectors. Pump Priming Eductor-E-PM-3501/3502. 2020. Available online: http://primetechejectors.com/pdf/pump_priming_eductor.pdf (accessed on 17 October 2020).
  19. Ullah, K.R.; Saidur, R.; Ping, H.W.; Akikur, R.K.; Shuvo, N.H. A review of solar thermal refrigeration and cooling methods. Renew. Sustain. Energy Rev. 2013, 24, 499–513.
  20. Vakiloroaya, V.; Samali, B.; Fakhar, A.; Pishghadam, K. A review of different strategies for HVAC energy saving. Energy Convers. Manag. 2014, 77, 738–754.
  21. Chunnanond, K.; Aphornratana, S. Ejectors: Applications in refrigeration technology. Renew. Sustain. Energy Rev. 2004, 8, 129–155.
  22. Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407.
  23. Fox Venturi Products, Pup Priming Ejectors, Fox Venturi Products. 2020. Available online: https://www.foxvalve.com/air-gas-steam-vacuum-ejectors/pump-priming-ejectors/ (accessed on 17 October 2020).
  24. SWT Water. Eductors. 2018. Available online: https://www.swtwater.com/catalog/eductors_index.htm (accessed on 7 September 2018).
  25. Cebeco. Products-Eductors. 2010. Available online: http://www.cebeco.com.au/products/eductors/jt-eductors (accessed on 28 July 2018).
  26. Schutte & Koerting. Eductors & Syphons–Water Jet Eductor. 2018. Available online: https://www.s-k.com/eductors-syphons/water-jet-eductors.cfm (accessed on 15 January 2020).
  27. Fox Valve, Fox Mini-Eductors. 2017. Available online: https://www.foxvalve.com/mini-eductors/introduction/ (accessed on 1 April 2021).
  28. Bamford & Morris Ltd. Custom Eductor Solutions for Pumping Gases. 2018. Available online: http://www.bamfordandmorris.com/eductors-for-gas.html (accessed on 15 January 2020).
  29. Applied Vacuum. Liquid Eductors. 2017. Available online: http://www.appliedvacuum.co.za/products/liquid-educators/ (accessed on 5 January 2020).
  30. Boysan, F. A Two-Fluid Model for Fluent; Flow Simulation Consultants Ltd.: Sheffield, UK, 1990.
  31. Oh, J.-T.; Ngoc, C.N. Development of heat pump system using thermobank and ejector for heating room and cold storage. In Electric Vehicles and the Future of Energy Efficient Transportation; IGI Global: Hershey, PA, USA, 2015; pp. 784–802.
  32. AB Progetti, Liquid Ejectors. 2018. Available online: http://www.abprogetti.com/liquid-ejectors.html (accessed on 25 December 2020).
  33. Elbel, S.; Hrnjak, P. Ejector Refrigenration: An Overview of Historical and Present Developments with an Emphasis on Air-Conditioning Applications. In Proceedings of the International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 14–17 July 2008.
  34. Chen, X.; Somer, S.; Worall, M.; Riffat, S. Recent developments in ejector refrigeration technologies. Renew. Sustain. Energy Rev. 2013, 19, 629–651.
  35. Eames, W. A new prescription for the design of supersonic jet-pumps: The constant rate of momentum change method. Applied Therm. Eng. 2002, 22, 71–87.
  36. Kitrattana, B.; Aphornratana, S.; Thongtip, T.; Ruangtrakoon, N. Comparison of traditional and CRMC ejector performance used in a steam ejector refrigeration. Energy Precedia 2017, 138, 476–481.
  37. Kumar, V.; Singhal, G.; Subbarao, P. Realization of novel constant rate of kinetic energy change (CRKEC) supersonic ejector. Energy 2018, 164, 694–706.
  38. Ariafar, K.; Toorani, A. Effect of nozzle geometry on a model thermocompressor performance—A numerical evaluation. In Proceedings of the Annual International Conference on Mechanical Engineering, Shiraz, Iran, 16–18 May 2012.
  39. Zare-Behtash, H.; Gongora-Orozco, N.; Kontis, K. Effect of primary jet geometry on ejector performance: A cold-flow investigation. Int. J. Heat Fluid Flow 2011, 32, 596–607.
  40. Sharifi, N.; Sharifi, M. Experimental improvement of ejector performance through numerical optimization of nozzle geometry. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013.
  41. Sag, N.B.; Ersoy, H.K. Experimental investigation on motive nozzle throat diameter for an ejector expasion refrigeration system. Energy Convers. Manag. 2016, 124, 1–12.
  42. Xue, K.; Li, K.; Chen, W.; Chong, D.; Yan, J. Numerical Investigation on the performance of different primary nozzle structures in the supersonic ejector. In Proceedings of the Eigth International Conference on Applied Energy, Beijing, China, 8–11 October 2016.
  43. Elhub, B.; Mat, S.; Sopian, K.; Elbreki, A.; Ruslan, M.H.; Ammar, A. Performance evaluation and parametric studies on variable nozzle ejector using R134A. Case Stud. Therm. Eng. 2018, 12, 258–270.
  44. Seckin, C. Investigation of the effect of the primary nozzle throat diameter on the evaporator performance of an Ejector expansion refrigeration cycle. J. Therm. Eng. 2018, 4, 1939–1953.
  45. Xu, J.; Zhozhou, C.; Chaobin, D.; Eiji, H. Study on the Performance of a Variable Geometry Ejector. In Proceedings of the 12th IEA Heat Pump Conference 2017, Rotterdam, The Netherlands, 15–18 May 2017.
  46. Zhang, S.; Shen, S.; Yang, Y. Numerical investigation on performance of the adjustable ejector. Int. J. Low Carbon Technol. 2010, 5, 51–56.
  47. Dong, J.; Ma, H.B. Study of optimum nozzle exit position (NXP) in a steam ejector refrigeration system. In Proceedings of the 7th International Symposium on Multiphase Flow, Heat Mass Transfer and Energy Conversion, Xi’an, China, 26–30 October 2013; pp. 115–123.
  48. Mani, K.; Tiwari, S.; Annamalai, M. Computational analysis of ejector with oscillating nozzle. In Proceedings of the International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 9–12 July 2018.
  49. Park, S. Enhancement of entraining performance on Thermal vapor compressor for Multi-Effect Desalination Plants by Swirl Effects of Motive Steam. Numer. Heat Transf. 2009, 56, 406–421.
  50. Yan, J.; Chong, D.; Wu, X. Effect of swirling vanes on performance of steam-water jet injector. Appl. Therm. Eng. 2010, 30, 623–630.
  51. Banu, P.; Mallikarjuna, J.M.; Mani, A. Experimental and numerical investigation of ejector jet refrigeration system with primary stream swirl. In Proceedings of the 16th International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 11–14 July 2016.
  52. Banu, P.; Tiwari, J.S.; Mani, A. Three-dimensional numerical investigations on ejector of vapour jet refrigeration system. In Proceedings of the Purdue Conference at Purdue, West Lafayette, IN, USA, 14–17 July 2014.
  53. Banu, J.P.; Mani, A. Numerical studies on ejector with swirl generator. Int. J. Therm. Sci. 2019, 137, 589–600.
  54. Gupta, K.; Lilley, D.G.; Syred, N. Swirl Flows; Abacus Press: Tunbridge Wells, UK, 1984.
  55. Chlappetta, L.; Verma, P.; Radcliff, T.D. Ejector with Motive Flow Swirl. Farmington Patent US2014/0083121 A1, 10 April 2012.
  56. Garris, A. Pressure Exchanging Ejector and Methods to Use. USA Patent US6138456A, 31 October 2000.
  57. Hong, W.J.; Alhussan, K.; Zhang, H.; Garris, C.A., Jr. A novel thermally driven rotor-vane/pressure-exchange ejector refrigeration system with environmental benefits and energy efficiency. Energy 2004, 29, 2331–2345.
  58. Hong, W.; Alhussan, K.; Garris, J.C. The supersonic/rotor-vane/pressure-exchange ejector. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2001.
  59. Alhussan, K.; Garris, C. Effect of Changing Throat Diameter Ratio on A Steam Supersonic Pressure Exchange Ejector. Mod. Phys. Lett. B 2005, 19, 1715–1718.
  60. Chaiwongsa, P.; Wongwises, S. Effect of throat diameters of the ejector on the performance of the refrigeration cycle using a two-phase ejector as an expansion device. Int. J. Refrig. 2007, 30, 601–608.
  61. Bi, R.; Hu, M.; Wang, S.; Tan, X.; Zheng, S. Effect of Throat Length on Stream Ejector Critical Back Pressure. Chem. Eng. Trans. 2017, 61, 1945–1950.
  62. Saini, S.; Yunus, R.; Nur, I. Effect of variations throat length on Ejector Performance. Int. J. Eng. Inf. Sci. Appl. Sci. 2018, 1, 1–6.
  63. Ren, Q.; Guo, X.M.; Guo, X.W.; Li, T.L. Experimental study on Performance of Two Phase Ejector Refrigeration cycle system with Two-throat Nozzle. In Proceedings of the International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 14–17 July 2014.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback