The traditional power system is inefficient because it entirely depends on fossil fuels, and having centralized generation that is far away from consumers. In these circumstances, the generated electricity needs to be transmitted and distributed to consumers via transmission and distribution lines over long distances, spending many resources on construction, maintenance of all systems involved and high levels of technical losses. In smart grid, energy management is an indispensable for reducing energy cost of consumers while maximizing user comfort and alleviating the peak to average ratio and carbon emission under real time pricing approach.
1. Introduction
The traditional power system is inefficient because it entirely depends on fossil fuels, and having centralized generation that is far away from consumers. In these circumstances, the generated electricity needs to be transmitted and distributed to consumers via transmission and distribution lines over long distances, spending many resources on construction, maintenance of all systems involved and high levels of technical losses
[1]. According to
[2], centralized power systems suffer from severe transmission and distribution energy losses because of long distances between consumers and generating stations. Furthermore, centralized generation usually causes more environmental pollution than distributed generation technologies. From the consumer’s point of view, practically, electricity is used in unintelligent manner without control. Keeping in view both perspectives, new paradigms of distributed generation and smart grid have emerged for electricity generation and consumption. These paradigms are prominent in the electricity market around the world because they have low transmission losses and provide electricity intelligently with control to consumers. According to
[1], the distributed generation definitely refers to microgrids, which is small-sized, near to consumers, and directly connected to the distribution system. Smart grids are power grids with advanced communication and control technologies between consumers and generating stations, delivering optimized power usage, clean energy at reduced cost, and improving the quality of energy and efficiency of the power grid. They also provide reductions in technical losses and greenhouse gas emissions, and solve the high carbon emissions problem, where 23% and 41% pollution emission is caused by transport sector, and energy sector, respectively, around the globe
[3]. Thus, the conventional power gird is not able to meet future electricity demand due to dependence on limited and environment foe fossil fuels.
With microgrids, evolution dependence on fossil fuels is reduced, and high carbon emission problem is resolved. Furthermore, the microgrid can be connected with smart homes in modes like grid-connected and islanded. In islanded mode, microgrids and commercial grids couldnot initiate the purchase/sell mechanism of energy. On the other hand, in grid-connected mode, the microgrid purchases and sells electricity from/to the external power grid. In the recent past, a significant variety of forecasts have been employed. The selection of a forecasting model is typically dependent on the available data, the model network mechanism’s aims, and the energy planning operation. In this paper, we examine renewable energy and power forecast models used as an energy planning tool in a critical and precise way, the application of these techniques for forecasting, their accuracy for geographical and temporal prediction, and their significance to policy and planning purposes are all explored. Machine learning models handling enormous data while also providing precise predictive analyses. By integrating various models and using ensemble methods, we may improve forecasting accuracy. Artificial neural networks, when utilised correctly, can help one make better decisions because they can extract and model previously unknown correlations and characteristics
[4]. The microgrid includes renewable energy sources (RES) such as solar, wind etc., to generate electricity, contributing to pollution emission minimization. Furthermore, RES are intermittent in nature; thus, one cannot rely on them. Therefore, ESSs and EVs are used with RES to solve this problem.
One of the problems to be catered within smart grid/smart home is energy management, whose purpose is to give greater control to the user’s over their power usage to promote the efficient use of electricity, which is possible with the implementation of demand response (DR). The DR is classified in two classes, namely: direct DR program, in which the electric utility company (EUC) operator disconnects or interrupts the load as per an interruption contract signed with the consumer; indirect DR program, where the consumer changes/adapts their demand in response to the offered pricing signaled by the EUC operator
[5]. The latter DR program is the focus of this work.
2. System Model
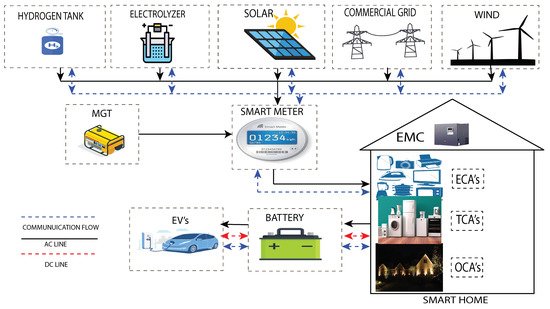
The proposed system model is composed of a residential smart home equipped with smart meter and smart appliances, and a smart microgrid comprising WT, PV panels, electrolyzer, and hydrogen tank. The proposed system model is depicted in Figure 1. However, residential consumers load and electricity generation of a microgrid is stochastic and uncertain. Thus, an ANN-mEDE-based prediction model is developed for efficient energy management. An efficient EMC based on ACO algorithm (whose control parameters are listed in Table 1) is installed to systematically schedule load and EVs charging/discharging connected to a smart microgrid according to RTP signal. In our proposed work, the simulation time T is assumed to be 1 day, which is split into sub-timeslots of equal duration denoted by t(1h). The detailed description of each component of the proposed system model is as follows.
Figure 1. Proposed system model schematic diagram.
Table 1. ACO Parameters.
| Technique |
Parameters |
Values |
| |
Number of Ants |
15 |
| |
Maximum number of Iterations |
250 |
| Ant Colony Optimization |
Evaporation Rate |
7 |
| |
Pheromone Factor |
3 |
| |
Stopping criteria |
When Maximum iteration reached |
3. Energy Generation Prediction Model
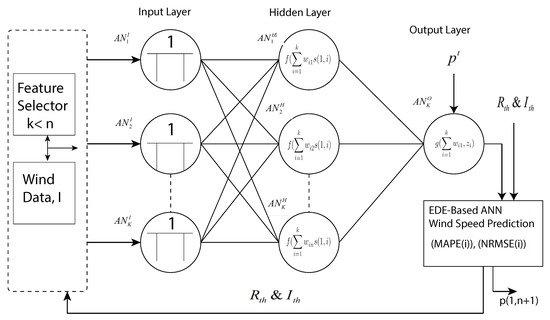
This section describes the prediction model to predict solar irradiation and wind speed for effective generation estimation. In this regard, a framework of ANN-mEDE is developed to predict solar irradiation and wind speed for effective estimation of generation. The proposed prediction model is composed of three parts: (i) feature selector, (ii) forecaster, and (iii) optimizer. Feature selector phase of the prediction model based on mutual information technique uses time-series solar irradiation and wind speed as input. The mutual information technique rank the inputs and passed the ranked inputs to redundancy and irrelevancy filters for the removal of irrelevant and redundant features. Then, the selected inputs are split into training and testing datasamples.
The forecaster phase is based on an artificial neural network (ANN), which uses training and testing sets to forecast solar irradiation and wind speed for a day-ahead time horizon. The ANN is a multilayer feed-forward network, where each succeeding layer gets input from the preceding layers. In other words, the outputs of one layer’s nodes are used as inputs in the next layer. A weighted linear combination is used to combine the inputs, which are changed by a nonlinear function
[6] to generate output.
The ANN has three layers layout having input, hidden, and output layers, where Artificial Neurons (ANs) in each layer are exploited by sigmoidal activation function
[7], which is shown in Equation (
1) as follows.
The input signal is S with attributes (as discussed in the first module). The parameter β is for steepness control of the activation function and b indicates the bias value. As discussed above, the developed prediction model is enabled via training to learn and accurately estimate future energy generation. In the literature, learning mechanisms such as unsupervised, supervised, and re-enforcement learning exist. The developed forecasting framework learns from time series analysis with the supervised learning approach, which employs multivariate autoregressive rules due to high convergence than benchmark learning rules
[8]. Solar irradiation and wind speed prediction model is illustrated in
Figure 2. The RESs three-year weather data is adopted from
[9]. The acquired data is divided into training and testing sets of 80% and 20%, respectively, as per the mechanism available
[10][11][12].
Figure 2. Solar irradiance and wind speed prediction model for estimation of electricity.
The training set trains the forecasting framework to predict future values, and testing set validates the forecasting framework to show the accuracy of the obtained predicted results compared to the ground-truth observations. Mean absolute percentage error (MAPE) is a validation metric (to illustrate the relationship between ANN predicted output and observed values), which is formulated as follows in Equation (
2)
[7].
Where pactual(i,j) denotes the actual and pforecast(i,j) represents forecasted solar irradiation and wind speed. m denotes number of days under observation. The control parameters are tuned using Levenburg Marquart algorithm until the error is minimized. The forecasted values (solar irradiation and wind speed) by ANN forecaster is fed to optimizer phase of the prediction model for further error minimization.
In the optimizer phase, the error is calculated between estimated and observed value, and this error is further minimized with the use of the mEDE algorithm in the optimizer phase. The meta-heuristic algorithms such as GA, PSO, FA, DE and GWO are widely used in prediction problems. The DE among these algorithms is selected due to its better performance in the aspects of fast converging speed, computational efficiency, and avoidance of premature convergence while seeking a global optimal solution. This better performance of DE is due to the different vector-based mechanism, which expands its search space
[13]. On this note, the authors of
[14][15][16][17] used DE and GA techniques, respectively; with this as motivation, we developed modified enhanced DE to optimize control parameters of the prediction model for returning accurate estimation without trapping into local optima and avoiding premature convergence. The energy estimations returned from the optimizer phase are more accurate and utilized for efficient energy management.
This entry is adapted from the peer-reviewed paper 10.3390/su132011429