Bio-Photonic Cavities: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Materials Science, Biomaterials | Biochemistry & Molecular Biology | Optics
Contributor:
Antonio De Luca

An eco-friendly approach to usual optical cavities, in which an electromagnetic radiation can release energy to matter by interacting with its molecular or atomic structure. Based on bio-inspired and biodegradable meta-surfaces, able to behave as a resonator for light, their optical response can be engineered at will to accomplish a particular optical task.  

  • bio-photonic cavities
  • quantum electrodynamic framework
  • light matter interaction

1. Resonant Meta-Surfaces

The first step toward the design of a bio-photonic cavity is to select the right optical resonator. If a bio-inspired approach has to be followed, commonly used materials for optoelectronics are excluded. In this case, indeed, due to the inability of common bio-inspired and biodegradable materials to behave like metals or dielectric mirrors, commonly used optoelectronic architectures are ruled out. New paradigms have to be explored, such as the so-called resonant meta-surfaces[1][2][3].
Meta-surfaces are novel nano-architectures whose performance and miniaturization capabilities are challenging the certainties of classic optics [4]. The prefix “meta” refers to meta-materials, the wider category to which meta-surfaces belong, since their properties go well beyond those of the constituent materials, and are mainly determined by their geometry. The term “surface”, instead, points out that these structures share a planar nature which is in perfect agreement with the use of biopolymers. In other words, meta-surfaces (MS) can be considered as nanostructured surfaces whose optical response can be engineered at will to accomplish a particular optical task. To achieve a specific functionality, meta-surfaces can rely on both metallic or dielectric nano-elements [5][6][7][8][9][10][11][12][13][14]. For our purposes, dielectric meta-surfaces are the ones of interest. Manifesting high-Q resonances in the visible range is only one of the results achievable with meta-surfaces [15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31][32].
One way to achieve a high-Q-resonant response by means of a meta-surface is to engineer a so-called “biperiodic” disk lattice [32]. Such a recently studied configuration relies on a particular lattice arrangement of high-refractive-index dielectric elements in which the unitary cell consists of two disks: a larger one, with a diameter equal to d + (Δ/2), and a smaller one, with a diameter of d − (Δ/2) (see Figure 1a). In the case reported in ref. [5] d = 92 nm, Δ is a spatial component to be added to d to obtain the large disk and to be subtracted to d to obtain the small disk. The asymmetry of the system can be evaluated via an “asymmetry parameter” α = Δ/d. In the case in which Δ = 0 nm (α = 0), corresponding to the mono-periodic lattice, no high-Q resonances are present in the transmittance spectrum (see Figure 1b, dashed line). When a small asymmetry is introduced between the two disks composing the unitary cell, such that Δ = 9.2 nm (α = 0.1), two steep minima in the transmittance spectrum arise, constituting the high-Q-factor resonances excited in the bi-periodic meta-surface. These resonances are found to possess a dipole-like character. In particular, the high-wavelength resonance has a magnetic-like character (mα), while the other has an electric-like character (pα). The Q-factor of these modes is about 500 and 1000, respectively, but it can be further increased by changing the asymmetry of the unitary cell.
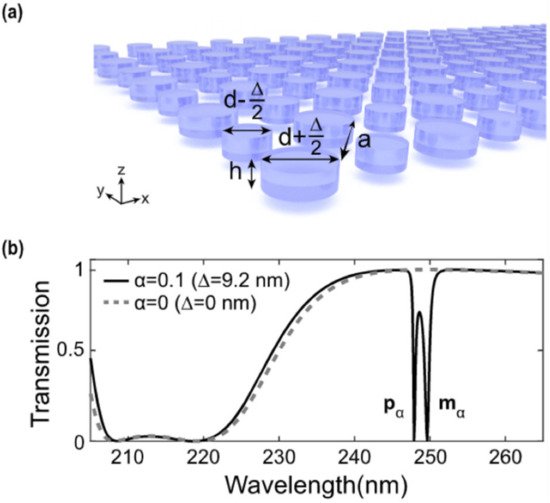
Photonics 08 00470 g002 550
Figure 1. Biperiodic meta-surfaces: (a) Sketch of a biperiodic meta-surface made of a larger element with a diameter equal to d + (Δ/2) and a smaller one of diameter d-(Δ/2). (b) Transmittance spectra belonging to two different cases. The first one, in which Δ = 0 (no biperiodicity), and the second one, in which Δ = 9.2 nm. In this latter case, two steep minima in the transmission spectrum of the structure are found, corresponding to the high-Q-factor resonances. Reproduced with permission from reference [32]. Copyright 2020, American Chemical Society.
Another remarkable example of high-Q-factor meta-surfaces are those in which the insurgence of resonances is governed by the so-called “Bound states In the Continuum” (BIC) [23][24][25][28][29][30][31][33][34][35][36][37][38]. BICs are common phenomena in many fields of physics, such as optics and acoustics. Let us consider, for example, the simple and general case of a wave propagating in the harmonic regime e−iωt. We also consider a certain generic potential which sustains a set of discrete bound states (see Figure 2). The discrete set of bound states sustained by the potential are the familiar cases of the bound states of an electron in an atom or the modes of a metal/insulator/metal cavity or those sustained by an optical fiber. Outside the “discrete” set, a set of modes exists in the “continuum” as scattered waves. In addition, locally confined waves with a complex frequency ω = ωa − iγ, ωa being the resonant frequency, can arise in the continuum coupled with propagating waves. These waves assume the shape of “leaky resonances”. Apart from these three cases, non-leaky bound states can exist in the continuum. These modes are known as “bound states in the continuum”. BICs can be considered as the ideal (γ = 0) case of a leaky resonance with no losses and an infinite quality factor. It is however true that such a wave would be characterized by a completely non-radiative nature, being by definition decoupled from a radiative leaky wave. As such, it would be impossible to excite BICs with free-space light. In practice, only low-loss BICs or “quasi-BIC” modes can be excited via free-space light illumination. The concept of a bound state in the continuum has been originally introduced in the field of quantum mechanics by Von Neumann and Wigner [39]. However, Fredrich and Wintgen generalized it in terms of a destructive interference between two resonances which would originally be decoupled, but that, as a consequence of the tuning of a particular parameter, can be brought to interact and strongly couple with each other [40].
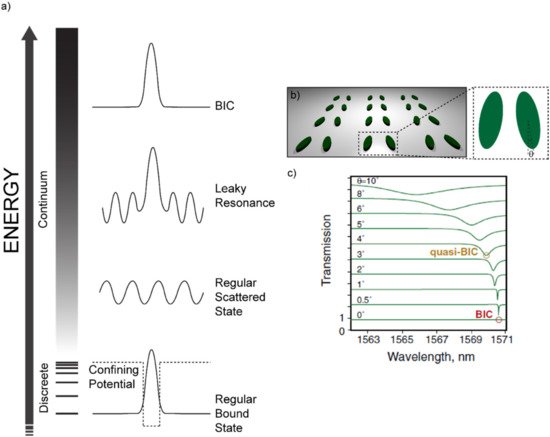
Photonics 08 00470 g003 550
Figure 2. Bound States in the Continuum: (a) Sketch of the possible states in the “discrete” and in the “continuum” sets. If a potential is structured in such a way that only a discrete set of modes is allowed, then regular bound states will appear due to the confinement action of the potential itself. If the energy is higher than the height of the potential barrier, a continuum of allowed states is accessed. The simplest and most probable state in the continuum is a regular scattered state. A so-called “leaky resonance” can occur in the continuum due to some kind of destructive interference phenomenon that suppresses some of the radiative channels and forms a bound state. Such a leaky bound state or leaky resonance is also coupled to a scattered (radiative) wave and, therefore, can be accessed by free-space light. In the end, a Bound State in the Continuum (BIC) can occur if the aforementioned mechanism for the leaky resonances suppresses all the radiative channels, thus forming an ideal bound state in the continuum. The illustration is inspired by reference [41]. (b) Sketch of the architecture re-drawn from references [42] and [30], evidencing the tilt angle θ as the tuning parameter to access the quasi-BIC visible as steep minima in the transmittance spectrum shown in (c). Reproduced from reference [30].
If the parameter that enables the coupling between these two modes intervenes on the symmetry of the system, we are in presence of a “symmetry-protected BIC”. These BICs are of special interest for the purpose of this review, since they occur in structures that can be readily replicated with a biopolymer through a soft-molding technique. Indeed, when a particular system holds a degree of symmetry (a reflection or rotational symmetry, for example), the modes with different symmetry classes are totally decoupled. However, if the symmetry is somehow broken, these modes can be brought to interact [41]. One noticeable example belonging to this family of symmetry-protected BICs consists in a lattice made of a zigzag array of tilted silicon resonators, as shown in Figure 2b [41]. The tuning parameter here is the tilt angle θ of the long axis of one of the facing elements. At θ = 0°, such a structure is found to have a symmetry-protected BIC that is impossible to excite through free-space light. However, while tilting θ, the symmetry is broken, and quasi-BIC modes become accessible. Such modes appear as steep minima in the transmission spectrum, whose Q-factor decreases while increasing θ and, as a consequence, departing from the perfect symmetry condition.
2. Biopolymers for Soft-Molding Processes
Polymers like Polydimethylsiloxane (PDMS) can be usually structured at the micro- and nano-scale via a technique called replica molding [43]. Through this process, any kind of nano-structure can be impressed over the polymer surface by simply pouring the polymeric liquid solution over a solid master, engineered with the “negative” shape [44][45][46][47][48].
Replica molding processes are usually carried out with soft elastomers like PDMS, which can be considered as a standard for these processes. Among all other properties, PDMS is also bio-compatible. Unfortunately, it is not biodegradable. Since the leitmotif of this review is to look for a reduction of the environmental footprint left by nano-technology, bio-inspired polymers are going to be targeted, keeping PDMS as a benchmark to be overcome. Natural biopolymers stand out for many aspects, including their light weight, excellent mechanical properties, biocompatibility, non-toxicity, low cost, etc. Thanks to these superior merits, natural functional biopolymers can be designed and optimized for the development of high-performance bio-photonic components [49]. Before describing in detail some of the most interesting technologically mature solutions, we list hereafter (Table 1) some of the many characteristics that make biopolymers the ideal choice as a bio-compatible scaffold with respect to classic soft elastomers [50][51][52]:
Table 1. Comparison between the proposed biopolymers with respect to PDMS.
  Polymer Silk Cellulose Hydrogel PDMS
Property  
Mechanical property Excellent Good Good Good
Optical clarity Excellent Excellent Very Good Moderate/Negative
Biocompatibility Excellent Excellent Excellent Good
Biodegradability Excellent Excellent Excellent Negative
Low absorption Excellent Excellent Moderate Negative
Tunable fluorescence     Moderate Negative
Rapid prototyping Moderate Moderate Moderate Negative

 

2.1 Silk

A special place in the family of bio-inspired polymers for optics is occupied by silk fibroin. Silk can be easily extracted from the cocoons of Bombyx mori Lepidoptera through a multistep procedure involving (i) silk cocoon degumming through a boiling process, (ii) dissolution in a salt solution and (iii) transformation in an aqueous solution via dialysis [53] (see Figure 3).
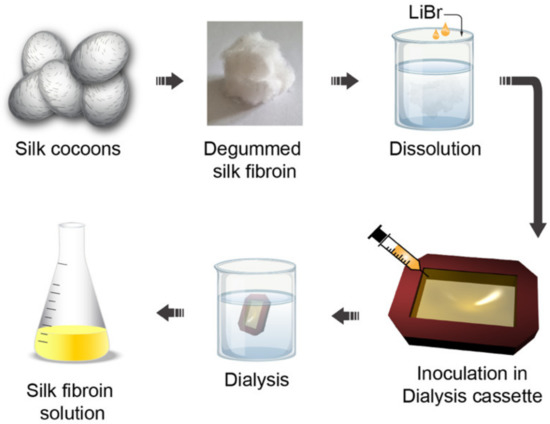
Photonics 08 00470 g004 550
Figure 3. Silk fibroin water solution fabrication: Silk cocoons are degummed through a boiling process and dissolved in a LiBr salt solution. The obtained solution is inoculated in a dialysis cassette and dialyzed for 48 h in ultrapure water. After that, the dialyzed solution is stirred to obtain the silk fibroin in aqueous solution. Inspired by references [53][54].
Once silk fibroin is obtained in an aqueous solution, it is readily available for the most variegated nano-engineering processes. Replica molding for microfluidic structures has probably been the first application on which micro-structured silk fibroin devices have been based [55][56][57].
The silk fibroin has also proved valuable as an all-water based Electron Beam (E-beam) resist, both positive and negative [58]. The two concurrent mechanisms that allow silk fibroin to behave as a positive (wash away the exposed area) or negative (wash away the non-exposed area) resist are (i) the formation of water-soluble peptides (in the case of the positive resist) and (ii) water radiolysis (for the negative case). In the former case, silk fibroin in an aqueous solution is crystallized to manifest water-insoluble properties. Under electron beam irradiation, the proteins composing such silk crystals degrade due to inelastic collisions with electrons. This process produces water-soluble peptides that can be easily washed away with water. In the latter case, water radiolysis, occurring as a consequence of high electron beam doses, induces a helicoidal folding of silk fibroin with the formation of intermolecular crosslinks that make the exposed area water-insoluble. The possibility to dope the silk fibroin’s aqueous solution with dyes like Green Fluorescent Protein (GFP), quantum dots and enzymes has been investigated with success, producing photoluminescent and bio-compatible E-beam resists.

2.2 Cellulose

An exceptional alternative to non-biodegradable polymers for replica molding applications is represented by cellulose. Cellulose consists of a chain of D-glucose units linked via a glycosidic bond, a particular kind of covalent bond that links the OH group of a sugar molecule to an atom or another molecule. In the case of cellulose, the glycosidic bond occurs between the OH group present on the C1 of the first monosaccharide and the C4 of the subsequent monosaccharide, by eliminating one water molecule to form a long polymeric chain. Hence, cellulose can be considered as the “polysaccharide” skeleton of a large part of the vegetable reign [59].
The textile industry, on its side, fostered a deep knowledge of cellulose chemistry to produce increasingly efficient filaments, like “viscose” [60]. There are mostly four pathways for the production of cellulose: (i) extraction from plants, (ii) bio-synthesis from bacteria, fungi and algae, (iii) in vitro cellulose synthesis and (iv) chemosynthesis by ring-opening polymerization. The first one is by far one of the most used. Relatively pure cellulose fibers can be extracted from cotton. However, if agro-wastes from, for example, cocoa, tomato pomace, and similar sources [61] have to be used within a circular economy framework, then purification techniques are mandatory. In these cases, a multistep procedure can be followed. As a first step, the vegetables from which cellulose must be extracted are dried in an oven overnight to remove water as well as other sugars and alcohol residuals. Then, the dried materials are dispersed in trifluoroacetic acid (TFA). The last step consists of centrifuging the solutions, so that the remaining clear solution can be easily cast over the desired substrate. In Figure 4, such a multistep procedure is illustrated together with films produced from cocoa pod husks, rice husks, parsley stem and spinach stem.
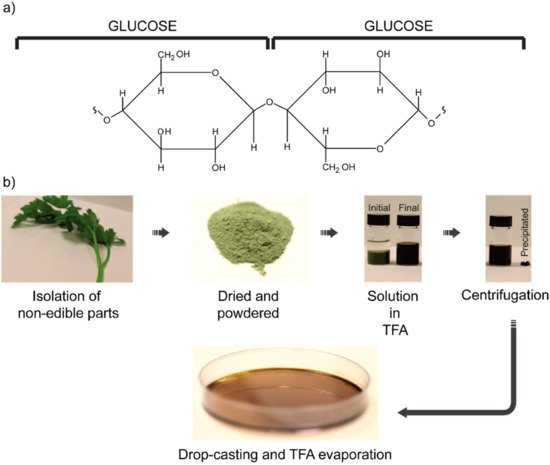
Photonics 08 00470 g006 550
Figure 4. Cellulose structure and preparation: (a) Cellulose polymeric chain formed via glycosidic bond between multiple D-glucose subunits. (b) Cellulose purification scheme for the achievement of bioplastics from non-edible agro-wastes. Powdered wastes from vegetables are dissolved in TFA, centrifuged and casted to let the solvent evaporate and obtain the film. Reproduced with permission from reference [61], Copyright 2014, American Chemical Society.
The obtained purified cellulose solution can be directly used to replicate micro- and nano-structures for high-end photonics. For example, purified cellulose has been recently used as a biodegradable and water-insoluble scaffold for the molding of photonic crystals and meta-surfaces in applications as optical diffraction gratings, structural dielectric colors, plasmonic resonators and Surface-Enhanced Raman Scattering (SERS) [62].
If additional water solubility is demanded, hydroxypropyl cellulose (HPC) can be used instead of the pure version [95]. HPC is a water-soluble substance derived from cellulose to which hydroxypropyl groups are added—a feature that, among the other chemical modifications, carries additional OH groups, which make HPC even more reactive than pure cellulose. HPC-based sub-micrometric structures have been produced via both hot embossing and replica-molding techniques, showing exceptional optical and plasmonic properties [63].

2.3 Hydrogels

Hydrogels represent an exceptional bio-inspired alternative to classic non-biodegradable polymers for soft molding lithography. Their outstanding bio-compatibility makes them the material of choice for biological applications. Moreover, their broad customizability in terms of mechanical and chemical properties makes them irreplaceable for tissue engineering, regenerative medicine and drug delivery [64][65][66][67][68][69][70][71][72][73][74][75][76][77]. Replica molding involving hydrogels is usually carried out by pouring a gel precursor over a solid-state master which is then immersed in the gelling agent [78]. However, improvements have been made to this technique by ensuring a controlled release of the gelling agent [77] (see Figure 5).
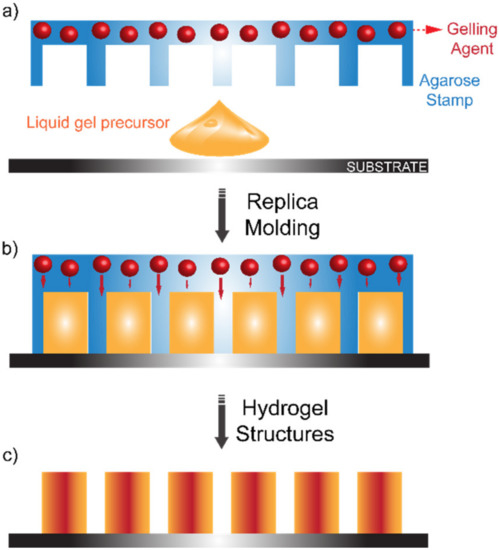
Photonics 08 00470 g008 550
Figure 5. Hydrogel Replica Molding: (a) A liquid gel precursor is poured over a substrate. (b) An agarose stamp embedding the gelling agent is then positioned over the casted liquid gel precursor to carry out a classic replica-molding procedure. The gelling agent is gradually released. (c) Once the gellification process is complete, the agarose stamp is removed and the gellified structures are produced. Reproduced with permission from reference [77], copyright 2006, American Chemical Society.
Biocompatible photonic hydrogels based on elastin-like polymers have been used as genetically engineered stimuli-responsive photonic hydrogels [79][80][81][82][83][84]. Bovine serum albumin hydrogel-based micro-optics have been fabricated via direct laser writing [85]. Stimuli-responsive hydrogels have been used to modify the shape of a liquid droplet serving as a microlens, mounted over the hydrogel itself [86].
Silk-based hydrogels have been successfully employed to produce lenses for Light-Emitting Diodes with a light extraction efficiency of over 95% [87]. A micropatterned glucose-responsive hydrogel made of a glucose-responsive material (3-(acrylamido)-phenylboronic acid), crosslinked to acrylamide and deposited over a silica optical fiber, was shown to be effective for glucose detection [87].
Among the wide zoo of hydrogels available for the replica molding process, the agarose-based ones are worth mentioning. A micro-scale replica molding with agarose over a PDMS stamp has been demonstrated in 2004 by Mayer et al. [88] Since then, optical devices such as planar waveguides or agarose-infiltrated optical fibers have been proposed [89][90][91].

This entry is adapted from the peer-reviewed paper 10.3390/photonics8110470

References

  1. Coppolaro, M.; Moccia, M.; Castaldi, G.; Alu, A.; Galdi, V. Surface-Wave Propagation on Non-Hermitian Metasurfaces with Extreme Anisotropy. IEEE Trans. Microw. Theory Tech. 2021, 69, 2060–2071. [Google Scholar] [CrossRef]
  2. Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
  3. Di Meo, V.; Moccia, M.; Sanità, G.; Crescitelli, A.; Lamberti, A.; Galdi, V.; Rendina, I.; Esposito, E. Advanced DNA Detection via Multispectral Plasmonic Metasurfaces. Front. Bioeng. Biotechnol. 2021, 9, 666121. [Google Scholar] [CrossRef]
  4. Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
  5. Shaltout, A.M.; Shalaev, V.M.; Brongersma, M.L. Spatiotemporal Light Control with Active Metasurfaces. Science 2019, 364, 298–302. [Google Scholar] [CrossRef]
  6. Krasnok, A.; Tymchenko, M.; Alù, A. Nonlinear Metasurfaces: A Paradigm Shift in Nonlinear Optics. Mater. Today 2018, 21, 8–21. [Google Scholar] [CrossRef]
  7. Wu, P.C.; Tsai, W.-Y.; Chen, W.T.; Huang, Y.-W.; Chen, T.-Y.; Chen, J.-W.; Liao, C.Y.; Chu, C.H.; Sun, G.; Tsai, D.P. Versatile Polarization Generation with an Aluminum Plasmonic Metasurface. Nano Lett. 2016, 17, 445–452. [Google Scholar] [CrossRef]
  8. Caligiuri, V.; De Sio, L.; Petti, L.; Capasso, R.; Rippa, M.; Maglione, M.G.; Tabiryan, N.; Umeton, C. Electro-/All-Optical Light Extraction in Gold Photonic Quasi-Crystals Layered with Photosensitive Liquid Crystals. Adv. Opt. Mater. 2014, 2, 950–955. [Google Scholar] [CrossRef]
  9. Kamali, S.M.; Arbabi, E.; Arbabi, A.; Faraon, A. A Review of Dielectric Optical Metasurfaces for Wavefront Control. Nanophotonics 2018, 7, 1041–1068. [Google Scholar] [CrossRef]
  10. Ding, F.; Pors, A.; Bozhevolnyi, S.I. Gradient Metasurfaces: A Review of Fundamentals and Applications. Rep. Prog. Phys. 2017, 81, 026401. [Google Scholar] [CrossRef]
  11. Kruk, S.; Kivshar, Y. Functional Meta-Optics and Nanophotonics Governed by Mie Resonances. ACS Photonics 2017, 4, 2638–2649. [Google Scholar] [CrossRef]
  12. Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F.; Paulson, J.A. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef] [PubMed]
  13. Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chu, C.H.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband Achromatic Optical Metasurface Devices. Nature Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
  14. Lininger, A.; Zhu, A.Y.; Park, J.-S.; Palermo, G.; Chatterjee, S.; Boyd, J.; Capasso, F.; Strangi, G. Optical Properties of Metasurfaces Infiltrated with Liquid Crystals. Proc. Natl. Acad. Sci. USA 2020, 117, 20390–20396. [Google Scholar] [CrossRef] [PubMed]
  15. Tuz, V.R.; Khardikov, V.V.; Kivshar, Y.S. All-Dielectric Resonant Metasurfaces with a Strong Toroidal Response. ACS Photonics 2018, 5, 1871–1876. [Google Scholar] [CrossRef]
  16. Santiago-Cruz, T.; Fedotova, A.; Sultanov, V.; Weissflog, M.A.; Arslan, D.; Younesi, M.; Pertsch, T.; Staude, I.; Setzpfandt, F.; Chekhova, M. Photon Pairs from Resonant Metasurfaces. Nano Lett. 2021, 21, 4429. [Google Scholar] [CrossRef]
  17. Zou, C.; Sautter, J.; Setzpfandt, F.; Staude, I. Resonant Dielectric Metasurfaces: Active Tuning and Nonlinear Effects. J. Phys. D Appl. Phys. 2019, 52, 373002. [Google Scholar] [CrossRef]
  18. Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically Resonant Dielectric Nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef] [PubMed]
  19. Staude, I.; Pertsch, T.; Kivshar, Y.S. All-Dielectric Resonant Meta-Optics Lightens Up. ACS Photonics 2019, 6, 802–814. [Google Scholar] [CrossRef]
  20. Pertsch, T.; Kivshar, Y. Nonlinear Optics with Resonant Metasurfaces. MRS Bull. 2020, 45, 210–220. [Google Scholar] [CrossRef]
  21. Overvig, A.; Alù, A. Wavefront-Selective Fano Resonant Metasurfaces. Adv. Photonics 2021, 3, 026002. [Google Scholar] [CrossRef]
  22. Zubyuk, V.; Carletti, L.; Shcherbakov, M.; Kruk, S. Resonant Dielectric Metasurfaces in Strong Optical Fields. APL Mater. 2021, 9, 60701. [Google Scholar] [CrossRef]
  23. Sadrieva, Z.F.; Sinev, I.S.; Koshelev, K.L.; Samusev, A.; Iorsh, I.V.; Takayama, O.; Malureanu, R.; Bogdanov, A.A.; Lavrinenko, A.V. Transition from Optical Bound States in the Continuum to Leaky Resonances: Role of Substrate and Roughness. ACS Photonics 2017, 4, 723–727. [Google Scholar] [CrossRef]
  24. Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating Photonics with Resonant Dielectric Nanostructures. Nanophotonics 2019, 8, 725–745. [Google Scholar] [CrossRef]
  25. Doeleman, H.M.; Monticone, F.; Den Hollander, W.; Alù, A.; Koenderink, A.F. Experimental Observation of a Polarization Vortex at an Optical Bound State in the Continuum. Nat. Photonics 2018, 12, 397–401. [Google Scholar] [CrossRef]
  26. Carletti, L.; Koshelev, K.; De Angelis, C.; Kivshar, Y. Giant Nonlinear Response at the Nanoscale Driven by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 033903. [Google Scholar] [CrossRef]
  27. Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive Hyperspectral Imaging and Biodetection Enabled by Dielectric Metasurfaces. Nat. Photonics 2019, 13, 390–396. [Google Scholar] [CrossRef]
  28. Ha, S.T.; Fu, Y.H.; Emani, N.K.; Pan, Z.; Bakker, R.M.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Directional Lasing in Resonant Semiconductor Nanoantenna Arrays. Nat. Nanotechnol. 2018, 13, 1042–1047. [Google Scholar] [CrossRef]
  29. Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High- Q Supercavity Modes in Subwavelength Dielectric Resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar] [CrossRef]
  30. Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric Metasurfaces with High- Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [PubMed]
  31. Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing Action from Photonic Bound States in Continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef] [PubMed]
  32. Hu, J.; Lawrence, M.; Dionne, J.A. High Quality Factor Dielectric Metasurfaces for Ultraviolet Circular Dichroism Spectroscopy. ACS Photonics 2020, 7, 36–42. [Google Scholar] [CrossRef]
  33. Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S.; et al. All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum. Adv. Mater. 2019, 31, 1901921. [Google Scholar] [CrossRef]
  34. He, Y.; Guo, G.; Feng, T.; Xu, Y.; Miroshnichenko, A.E. Toroidal Dipole Bound States in the Continuum. Phys. Rev. B 2018, 98, 161112. [Google Scholar] [CrossRef]
  35. Gomis-Bresco, J.; Artigas, D.; Torner, L. Anisotropy-Induced Photonic Bound States in the Continuum. Nature Photonics 2017, 11, 232–236. [Google Scholar] [CrossRef]
  36. Koshelev, K.; Bogdanov, A.; Kivshar, Y. Meta-Optics and Bound States in the Continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef]
  37. Azzam, S.I.; Shalaev, V.M.; Boltasseva, A.; Kildishev, A.V. Formation of Bound States in the Continuum in Hybrid Plasmonic-Photonic Systems. Phys. Rev. Lett. 2018, 121, 253901. [Google Scholar] [CrossRef]
  38. Jin, J.; Yin, X.; Ni, L.; Soljačić, M.; Zhen, B.; Peng, C. Topologically Enabled Ultrahigh- Q Guided Resonances Robust to out-of-Plane Scattering. Nature 2019, 574, 501–504. [Google Scholar] [CrossRef] [PubMed]
  39. Von Neuman, J.; Wigner, E.; von Neuman, J.; Wigner, E. Uber Merkwürdige Diskrete Eigenwerte. Uber Das Verhalten von Eigenwerten Bei Adiabatischen Prozessen. PhyZ 1929, 30, 467–470. [Google Scholar]
  40. Friedrich, H.; Wintgen, D. Interfering Resonances and Bound States in the Continuum. Phys. Rev. A 1985, 32, 3231. [Google Scholar] [CrossRef]
  41. Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound States in the Continuum. Nature Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
  42. Tittl, A.; Leitis, A.; Liu, M.; Yesilkoy, F.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging-Based Molecular Barcoding with Pixelated Dielectric Metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar] [CrossRef]
  43. Xia, Y.; Whitesides, G.M. Soft Lithography. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
  44. Qin, D.; Xia, Y.; Whitesides, G.M. Soft Lithography for Micro- and Nanoscale Patterning. Nat. Protoc. 2010, 5, 491–502. [Google Scholar] [CrossRef] [PubMed]
  45. Ahadian, S.; Civitarese, R.; Bannerman, D.; Mohammadi, M.H.; Lu, R.; Wang, E.; Davenport-Huyer, L.; Lai, B.; Zhang, B.; Zhao, Y.; et al. Organ-On-A-Chip Platforms: A Convergence of Advanced Materials, Cells, and Microscale Technologies. Adv. Healthc. Mater. 2018, 7, 1700506. [Google Scholar] [CrossRef] [PubMed]
  46. Yuk, H.; Lu, B.; Lin, S.; Qu, K.; Xu, J.; Luo, J.; Zhao, X. 3D Printing of Conducting Polymers. Nat. Commun. 2020, 11, 1604. [Google Scholar] [CrossRef]
  47. Cataldi, U.; Caputo, R.; Kurylyak, Y.; Klein, G.; Chekini, M.; Umeton, C.; Bürgi, T. Growing Gold Nanoparticles on a Flexible Substrate to Enable Simple Mechanical Control of Their Plasmonic Coupling. J. Mater. Chem. C 2014, 2, 7927–7933. [Google Scholar] [CrossRef]
  48. Wolf, M.P.; Salieb-Beugelaar, G.B.; Hunziker, P. PDMS with Designer Functionalities—Properties, Modifications Strategies, and Applications. Prog. Polym. Sci. 2018, 83, 97–134. [Google Scholar] [CrossRef]
  49. Wang, Z.; Ma, Z.; Sun, J.; Yan, Y.; Bu, M.; Huo, Y.; Li, Y.-F.; Hu, N. Recent Advances in Natural Functional Biopolymers and Their Applications of Electronic Skins and Flexible Strain Sensors. Polymers 2021, 13, 813. [Google Scholar] [CrossRef]
  50. Campbell, S.B.; Wu, Q.; Yazbeck, J.; Liu, C.; Okhovatian, S.; Radisic, M. Beyond Polydimethylsiloxane: Alternative Materials for Fabrication of Organ-on-a-Chip Devices and Microphysiological Systems. ACS Biomater. Sci. Eng. 2020, 7, 2880–2899. [Google Scholar] [CrossRef]
  51. Shan, D.; Gerhard, E.; Zhang, C.; Tierney, J.W.; Xie, D.; Liu, Z.; Yang, J. Polymeric Biomaterials for Biophotonic Applications. Bioact. Mater. 2018, 3, 434–445. [Google Scholar] [CrossRef]
  52. Omenetto, F.G.; Kaplan, D.L. A New Route for Silk. Nat. Photonics 2008, 2, 641–643. [Google Scholar] [CrossRef]
  53. Guidetti, G.; Wang, Y.; Omenetto, F.G. Active Optics with Silk. Nanophotonics 2020, 10, 137–148. [Google Scholar] [CrossRef]
  54. Rockwood, D.N.; Preda, R.C.; Yücel, T.; Wang, X.; Lovett, M.L.; Kaplan, D.L. Materials Fabrication from Bombyx Mori Silk Fibroin. Nature Protoc. 2011, 6, 1612–1631. [Google Scholar] [CrossRef]
  55. Bettinger, C.J.; Cyr, K.M.; Matsumoto, A.; Langer, R.; Borenstein, J.T.; Kaplan, D.L. Silk Fibroin Microfluidic Devices. Adv. Mater. 2007, 19, 2847–2850. [Google Scholar] [CrossRef] [PubMed]
  56. Xu, M.; Pradhan, S.; Agostinacchio, F.; Pal, R.K.; Greco, G.; Mazzolai, B.; Pugno, N.M.; Motta, A.; Yadavalli, V.K. Easy, Scalable, Robust, Micropatterned Silk Fibroin Cell Substrates. Adv. Mater. Interfaces 2019, 6, 1801822. [Google Scholar] [CrossRef]
  57. Pal, R.K.; Kurland, N.E.; Wang, C.; Kundu, S.C.; Yadavalli, V.K. Biopatterning of Silk Proteins for Soft Micro-Optics. ACS Appl. Mater. Interfaces 2015, 7, 8809–8816. [Google Scholar] [CrossRef] [PubMed]
  58. Kim, S.; Marelli, B.; Brenckle, M.A.; Mitropoulos, A.N.; Gil, E.S.; Tsioris, K.; Tao, H.; Kaplan, D.L.; Omenetto, F.G. All-Water-Based Electron-Beam Lithography Using Silk as a Resist. Nat. Nanotechnol. 2014, 9, 306–310. [Google Scholar] [CrossRef]
  59. Klemm, D.; Heublein, B.; Fink, H.P.; Bohn, A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef]
  60. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley: Hoboken, NJ, USA, 2000.
  61. Bayer, I.S.; Guzman-Puyol, S.; Heredia-Guerrero, J.A.; Ceseracciu, L.; Pignatelli, F.; Ruffilli, R.; Cingolani, R.; Athanassiou, A. Direct Transformation of Edible Vegetable Waste into Bioplastics. Macromolecules 2014, 47, 5135–5143. [Google Scholar] [CrossRef]
  62. Caligiuri, V.; Tedeschi, G.; Palei, M.; Miscuglio, M.; Martin-Garcia, B.; Guzman-Puyol, S.; Hedayati, M.K.; Kristensen, A.; Athanassiou, A.; Cingolani, R.; et al. Biodegradable and Insoluble Cellulose Photonic Crystals and Metasurfaces. ACS Nano 2020, 14, 9502–9511. [Google Scholar] [CrossRef] [PubMed]
  63. Espinha, A.; Dore, C.; Matricardi, C.; Alonso, M.I.; Goñi, A.R.; Mihi, A. Hydroxypropyl Cellulose Photonic Architectures by Soft Nanoimprinting Lithography. Nat. Photonics 2018, 12, 343–348. [Google Scholar] [CrossRef]
  64. Peppas, N.A.; Hilt, J.Z.; Khademhosseini, A.; Langer, R. Hydrogels in Biology and Medicine: From Molecular Principles to Bionanotechnology. Adv. Mater. 2006, 18, 1345–1360. [Google Scholar] [CrossRef]
  65. Slaughter, B.V.; Khurshid, S.S.; Fisher, O.Z.; Khademhosseini, A.; Peppas, N.A. Hydrogels in Regenerative Medicine. Adv. Mater. 2009, 21, 3307–3329. [Google Scholar] [CrossRef] [PubMed]
  66. Kobayashi, H.; Ikada, Y.; Moritera, T.; Ogura, Y.; Honda, Y. Collagen-Immobilized Hydrogel as a Material for Lamellar Keratoplasty. J. Appl. Biomater. Off. J. Soc. Biomater. 1991, 2, 261–267. [Google Scholar] [CrossRef] [PubMed]
  67. Freed, L.E.; Marquis, J.C.; Nohria, A.; Emmanual, J.; Mikos, A.G.; Langer, R. Neocartilage Formation in Vitro and in Vivo Using Cells Cultured on Synthetic Biodegradable Polymers. J. Biomed. Mater. Res. 1993, 27, 11–23. [Google Scholar] [CrossRef]
  68. Sui, Z.; King, W.J.; Murphy, W.L. Protein-Based Hydrogels with Tunable Dynamic Responses. Adv. Funct. Mater. 2008, 18, 1824–1831. [Google Scholar] [CrossRef]
  69. Tang, Z.; Wang, Y.; Podsiadlo, P.; Kotov, N.A. Biomedical Applications of Layer-by-Layer Assembly: From Biomimetics to Tissue Engineering. Adv. Mater. 2006, 18, 3203–3224. [Google Scholar] [CrossRef]
  70. McGuigan, A.P.; Sefton, M.V. Vascularized Organoid Engineered by Modular Assembly Enables Blood Perfusion. Proc. Natl. Acad. Sci. USA 2006, 103, 11461–11466. [Google Scholar] [CrossRef]
  71. Nerem, R.M. Cellular Engineering. Ann. Biomed. Eng. 1991, 19, 529–545. [Google Scholar] [CrossRef]
  72. Langer, R. New Methods of Drug Delivery. Science 1990, 249, 1527–1533. [Google Scholar] [CrossRef]
  73. Buschmann, M.D.; Gluzband, Y.A.; Grodzinsky, A.J.; Kimura, J.H.; Hunziker, E.B. Chondrocytes in Agarose Culture Synthesize a Mechanically Functional Extracellular Matrix. J. Orthop. Res. 1992, 10, 745–758. [Google Scholar] [CrossRef] [PubMed]
  74. Sawhney, A.S.; Hubbell, J.A. Poly(Ethylene Oxide)-Graft-Poly(L-Lysine) Copolymers to Enhance the Biocompatibility of Poly(L-Lysine)-Alginate Microcapsule Membranes. Biomaterials 1992, 13, 863–870. [Google Scholar] [CrossRef]
  75. Langer, R.; Vacanti, J.P. Tissue Engineering. Science 1993, 260, 920–926. [Google Scholar] [CrossRef]
  76. Langer, R.; Peppas, N.A. Advances in Biomaterials, Drug Delivery, and Bionanotechnology. AIChE J. 2003, 49, 2990–3006. [Google Scholar] [CrossRef]
  77. Franzesi, G.T.; Ni, B.; Ling, Y.; Khademhosseini, A. A Controlled-Release Strategy for the Generation of Cross-Linked Hydrogel Microstructures. J. Am. Chem. Soc. 2006, 128, 15064–15065. [Google Scholar] [CrossRef] [PubMed]
  78. Cabodi, M.; Choi, N.W.; Gleghorn, J.P.; Lee, C.S.D.; Bonassar, L.J.; Stroock, A.D. A Microfluidic Biomaterial. J. Am. Chem. Soc. 2005, 127, 13788–13789. [Google Scholar] [CrossRef]
  79. Balog, E.R.M.; Ghosh, K.; Park, Y.I.; Hartung, V.; Sista, P.; Rocha, R.C.; Wang, H.L.; Martinez, J.S. Stimuli-Responsive Genetically Engineered Polymer Hydrogel Demonstrates Emergent Optical Responses. ACS Biomater. Sci. Eng. 2016, 2, 1135–1142. [Google Scholar] [CrossRef]
  80. Wang, E.; Desai, M.S.; Lee, S.W. Light-Controlled Graphene-Elastin Composite Hydrogel Actuators. Nano Lett. 2013, 13, 2826–2830. [Google Scholar] [CrossRef] [PubMed]
  81. Gulrez, S.K.; Al-Assaf, S.; Phillips, G.O. Hydrogels: Methods of Preparation, Characterisation and Applications. In Progress in Molecular and Environmental Bioengineering—From Analysis and Modeling to Technology Applications; InTech: London, UK, 2011. [Google Scholar]
  82. Alonso, M.; Reboto, V.; Guiscardo, L.; San Martín, A.; Rodríguez-Cabello, J.C. Spiropyran Derivative of an Elastin-like Bioelastic Polymer: Photoresponsive Molecular Machine to Convert Sunlight into Mechanical Work. Macromolecules 2000, 33, 9480–9482. [Google Scholar] [CrossRef]
  83. Annabi, N.; Mithieux, S.M.; Weiss, A.S.; Dehghani, F. The Fabrication of Elastin-Based Hydrogels Using High Pressure CO2. Biomaterials 2009, 30, 1–7. [Google Scholar] [CrossRef]
  84. Sun, Z.; Qin, G.; Xia, X.; Cronin-Golomb, M.; Omenetto, F.G.; Kaplan, D.L. Photoresponsive Retinal-Modified Silk-Elastin Copolymer. J. Am. Chem. Soc. 2013, 135, 3675–3679. [Google Scholar] [CrossRef] [PubMed]
  85. Sun, Y.L.; Dong, W.F.; Niu, L.G.; Jiang, T.; Liu, D.X.; Zhang, L.; Wang, Y.S.; Chen, Q.D.; Kim, D.P.; Sun, H.B. Protein-Based Soft Micro-Optics Fabricated by Femtosecond Laser Direct Writing. Light Sci. Appl. 2014, 3, e129. [Google Scholar] [CrossRef]
  86. Dong, L.; Agarwal, A.K.; Beebe, D.J.; Jiang, H. Adaptive Liquid Microlenses Activated by Stimuli-Responsive Hydrogels. Nature 2006, 442, 551–554. [Google Scholar] [CrossRef] [PubMed]
  87. Melikov, R.; Press, D.A.; Kumar, B.G.; Dogru, I.B.; Sadeghi, S.; Chirea, M.; Yilgör, I.; Nizamoglu, S. Silk-Hydrogel Lenses for Light-Emitting Diodes. Sci. Rep. 2017, 7, 7258. [Google Scholar] [CrossRef]
  88. Mayer, M.; Yang, J.; Gitlin, I.; Gracias, D.H.; Whitesides, G.M. Micropatterned Agarose Gels for Stamping Arrays of Proteins and Gradients of Proteins. GM Proteom. 2004, 4, 2366. [Google Scholar] [CrossRef]
  89. Jain, A.; Yang, A.H.J.; Erickson, D. Gel-Based Optical Waveguides with Live Cell Encapsulation and Integrated Microfluidics. Opt. Lett. 2012, 37, 1472. [Google Scholar] [CrossRef]
  90. Fujiwara, E.; Cabral, T.D.; Sato, M.; Oku, H.; Cordeiro, C.M.B. Agarose-Based Structured Optical Fibre. Sci. Rep. 2020, 10, 7035. [Google Scholar] [CrossRef]
  91. Gao, R.; Jiang, Y.; Ding, W. Agarose Gel Filled Temperature-Insensitive Photonic Crystal Fibers Humidity Sensor Based on the Tunable Coupling Ratio. Sens. Actuators B Chem. 2014, 195, 313–319. [Google Scholar] [CrossRef]
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback