You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Chemical
Water activity is one of the most important factors influencing the quality and stability of food, cosmetic, and pharmaceutical products.
- water activity
- sugars
- polyols
- Norrish model
1. Introduction
Water activity is one of the most important factors influencing the quality and stability of food, cosmetic, and pharmaceutical products [1,2,3]. Most of the studies on water activity have been carried out on food products, since this quantity has a significant effect on microbial stability, shelf life, and organoleptic characteristics [4].
Formal recognition of the importance of water activity dates back to the early 1950s, when Scott conducted a pioneering study showing that microbial growth and toxin production in food products were dependent on the activity, not the content, of water [5].
Although water activity can be rigorously defined in thermodynamic terms [6], its molecular origin is still far from being understood, as evidenced by the existence of different and sometimes conflicting explanations [7]. The most popular is that of “free water”, according to which water activity reflects its availability as a solvent or reagent, which results from the interactions between water molecules [8]. Another explanation attributes its origin to the structuring or ordering of water molecules induced by a solute [9]. In particular, a solute can behave as a “structure maker” or a “structure breaker”, depending on its ability to enhance or weaken the hydrogen-bonded water network. A further interpretation is based on the concepts of solute clustering and hydration number, that is, the number of water molecules close to the solute [10].
Despite the molecular significance of water activity remaining somewhat elusive, the importance of evaluating this quantity for the systems of interest is evident. For this purpose, many empirical and semi-empirical models have been developed [8,11,12]. One of the most used is the Norrish model, which provides a good compromise between accuracy and simplicity [13]. For a single-solute system, this model contains only one parameter, known as the Norrish constant, which can be easily determined from experimental data. However, in many situations, it may be necessary to estimate water activity in the absence of experimental information.
Molecular descriptors are numeric quantities associated with some structural feature or property of a molecule [14]. The use of these descriptors for property prediction has its basis in the principle of similarity, according to which similar molecular structures have similar chemical properties, just as different molecular structures have different chemical properties. Over the years, thousands of molecular descriptors have been used to predict the properties of various substances [15]. They can be classified into the following main categories [16,17]: constitutional; topological; geometrical; and quantum–chemical descriptors. Constitutional descriptors of a compound are based on the number and types of atoms, bonds, rings, etc., in its molecule. Topological descriptors are related to the two-dimensional structure of the molecule, which is regarded as a graph, with vertices representing atoms and edges representing bonds. Geometrical descriptors are derived from the three-dimensional structure of the molecule and consider different molecular features, such as molecular volume, total surface area, and solvent-accessible surface area. Finally, quantum–chemical descriptors are obtained from quantum–mechanical calculations aimed at characterizing the electronic properties of the molecule.
2. Correlation of Water Activity Data
For a single-solute system, the Norrish model provides the following expression for the dependence of water activity (aw) on composition:
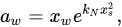
where kN is the Norrish constant, xw is the mole fraction of water, and xs is the mole fraction of the solute. Equation (1) can be derived rigorously from the Kirkwood–Buff theory of solutions, where the thermodynamic meaning of kN can also be deduced.
The correlation of water activity data by Equation (1) was performed by minimization of the following objective function:
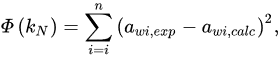
where n is the number of points of each data set, and the subscripts exp and calc indicate experimental and calculated values. Since the latter depend on the Norrish constant, it follows that Φ = f(kN). The results of the estimation procedure are summarized in Table 1, where the mean absolute error, defined as:
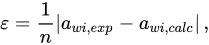
is also reported. The excellent agreement between experimental and calculated results (2.71 × 10−4 ≤ ε ≤ 1.35 × 10−3) clearly attests the suitability of the Norrish model to describe the activity of water in the investigated systems.
Table 1. Estimated Norrish constant values (∆xs: experimental range of solute mole fractions; kN: Norrish constant; Φmin: minimum value of the objective function; ε: mean absolute error).
| Solute | ∆xs | kN | Φmin | ε |
|---|---|---|---|---|
| Glucose | 0.023–0.111 | −2.920 | 1.71 × 10−5 | 1.00 × 10−3 |
| Fructose | 0.026–0.142 | −2.351 | 6.76 × 10−6 | 6.64 × 10−4 |
| Xylose | 0.020–0.059 | −2.196 | 1.30 × 10−6 | 2.71 × 10−4 |
| Sucrose | 0.018–0.098 | −6.777 | 6.87 × 10−6 | 5.85 × 10−4 |
| Sorbitol | 0.018–0.113 | −2.494 | 4.18 × 10−5 | 1.35 × 10−3 |
| Xylitol | 0.020–0.112 | −2.221 | 1.12 × 10−6 | 7.46 × 10−4 |
| Glycerol | 0.010–0.312 | −0.908 | 1.65 × 10−5 | 9.70 × 10−4 |
| Erythritol | 0.007–0.069 | −0.950 | 4.28 × 10−6 | 7.08 × 10−4 |
3. Use of Molecular Descriptors for the Prediction of the Norrish Constant
Different molecular descriptors were examined for their ability to predict the Norrish constant, with a focus on the classes of constitutional and topological indices.
Constitutional indices are zero-dimensional descriptors. They are the simplest and most used descriptors of a molecule, since they relate to easily determinable molecular features, such as the type of atoms, functional groups, bonds, or number of rings. In this study, the total information index on atomic composition (IAC) was selected to describe the constitutional properties of the solutes. IAC provides information about the type of atoms present in the molecule. This was the first theoretical information index introduced by Dancoff and Quastler in the early 1950s [21]. Since then, an increasing number of studies has revealed the importance of this and other composition-related descriptors in the development of structure–property relationships [22].
Topological indices are two-dimensional descriptors derived from the topological representation of a molecule. In recent decades, molecular topology has emerged as a powerful approach to evaluate structure–activity relationships [23], especially in the fields of pharmacology and toxicology [24,25]. According to this approach, molecular structures are described in terms of the mathematical properties of their associated graphs. For organic compounds, H-depleted graphs (i.e., graphs not including hydrogen atoms) are usually considered, due to the supposed limited contribution of these atoms to molecular connectivity. In this study, the first Zagreb index (Z1) was selected as a measure of molecular connectivity. Z1 belongs to the class of the Kier–Hall connectivity indices, and is one of the oldest and most studied topological descriptors [26]. It is related to the concept of vertex valency, and therefore characterizes the degree of atomic branching in the molecule.
With respect to the solutes examined here, it is interesting to consider that glucose and fructose, being isomers, have the same chemical formula. Accordingly, they are characterized by the same IAC value. However, their molecular connectivity shows some differences, which are reflected in the different values of Z1. In other words, contrary to the information index on atomic composition, the Zagreb index allows for discrimination between the two isomers. This is an important point to highlight since, as can be seen from the experimental activity data and the estimated Norrish constants (Table 1), the two solutes affect the activity of water differently.
To express the dependence of the Norrish constant on the selected descriptors, two empirical models were initially used: the linear model and the exponential model. They are described, respectively, by Equations (4) and (5):
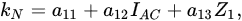

Both models contain three parameters, which were estimated by the least-squares procedure, yielding the results presented in Table 2. The quality of correlation was evaluated by calculating the following quantity:
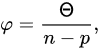
where  is the sum of squared errors between experimental and calculated Norrish constants, n is the number of data points, and p is the number of model parameters. It can be noticed that ϕ represents an estimate of the model variance, and can therefore be related to the predictive accuracy of the model.
is the sum of squared errors between experimental and calculated Norrish constants, n is the number of data points, and p is the number of model parameters. It can be noticed that ϕ represents an estimate of the model variance, and can therefore be related to the predictive accuracy of the model.
 is the sum of squared errors between experimental and calculated Norrish constants, n is the number of data points, and p is the number of model parameters. It can be noticed that ϕ represents an estimate of the model variance, and can therefore be related to the predictive accuracy of the model.
is the sum of squared errors between experimental and calculated Norrish constants, n is the number of data points, and p is the number of model parameters. It can be noticed that ϕ represents an estimate of the model variance, and can therefore be related to the predictive accuracy of the model.Table 2. Estimated parameters of the models for predicting the Norrish constant (kN) from information indices (IAC: information index on atomic composition; Z1: first Zagreb index; G: global information index; Θ: sum of squared errors; ϕ: statistical quantity defined by Equation (6)).


This entry is adapted from the peer-reviewed paper 10.3390/ijms222011044
This entry is offline, you can click here to edit this entry!
