AI-Assisted Design-on-Simulation for Life Prediction: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Computer Science, Artificial Intelligence | Materials Science, Biomaterials
Contributor:
Kuo-Ning Chiang

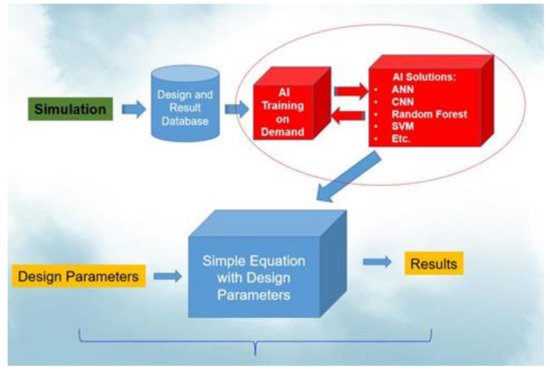
Many researchers have adopted the finite-element-based design-on-simulation (DoS) technology for the reliability assessment of electronic packaging. DoS technology can effectively shorten the design cycle, reduce costs, and effectively optimize the packaging structure. However, the simulation analysis results are highly dependent on the individual researcher and are usually inconsistent between them. Artificial intelligence (AI) can help researchers avoid the shortcomings of the human factor. 

  • FEM simulation
  • WLP
  • AI
  • machine learning
  • ANN
  • RNN
  • SVR
  • KRR
  • KNN
  • RF
  • regression model

1. Introduction

Electronics packaging plays an important role in the semiconductor industry. Currently, the mainstream electronic packaging structures include heterogeneous packaging, 3D packaging, system-in-packaging (SiP), fan-out (FO) packaging, and wafer-level packaging [1][2][3][4][5][6][7][8]. With the increasing complexity of packaging structures, manufacturing reliability test vehicles, and conducting ATCT experiments have become time-consuming and very expensive processes, the design-on-experiment (DoE) methodology for packaging design is becoming infeasible. As a result of the wide adoption of finite element analysis [9][10][11][12][13][14][15], accelerated thermal cycling tests are reduced significantly in the semiconductor industry, and package development time and cost are reduced as well. In a 3D WLP model, Liu [16] applied the Coffin–Manson life prediction empirical model to predict the reliability life of a solder joint within an accurate range. However, the results of finite element simulations are highly dependent on the mesh size, and there is no guideline to help researchers address this issue. Therefore, Chiang et al. [17] proposed the concept of “volume-weighted averaging” to determine the local strain, especially in critical areas. Tsou [18] successfully predicted packaging reliability through finite element simulation with a fixed mesh size in the critical area of the WLP structure. However, the results of simulation analysis are highly dependent on the individual researcher, and the results are usually inconsistent between simulations. In order to overcome this problem, the present work comparatively reviews an artificial intelligence (AI) approach in which electronic packaging design using a machine learning algorithm [19][20]. The use of machine learning for the analysis of electronic packaging reliability is the best way to obtain a reliable prediction result and meet the time-to-market demand.

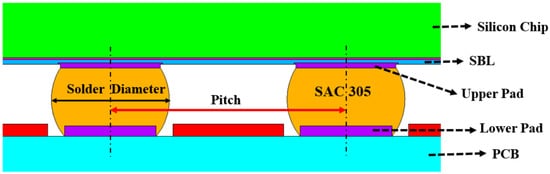
2. Finite Element Method for WLP

If the simulation consistently predicts the result of the experiment [21], then the simulation is an experiment; the experimental work can be replaced by a validated simulation procedure to create a large database for AI training and obtain a small and accurate AI model for reliability life cycles prediction. Once we obtain the final AI model for a new WLP structure, developers can simply input the WLP geometries, and then the life cycle can be obtained. Figure 1 illustrates this procedure.
Materials 14 05342 g001 550
Figure 1. AI-assisted design-on-simulation procedure.
In the simulation process, the solder material was a nonlinear plastic material. Therefore, PLANE182, which has good convergence characteristics and can deal with large deformations, was used as the solder ball element. Figure 2 shows the stress–strain curve for an Sn–Ag–Cu (SAC)305 solder joint. The stress–strain curve [22], obtained by tensile testing and the Chabochee kinematic hardening model, was used to describe the tensile curves at different temperatures. Once the model is built, boundary conditions and external thermal loading are required for the WLP simulation.
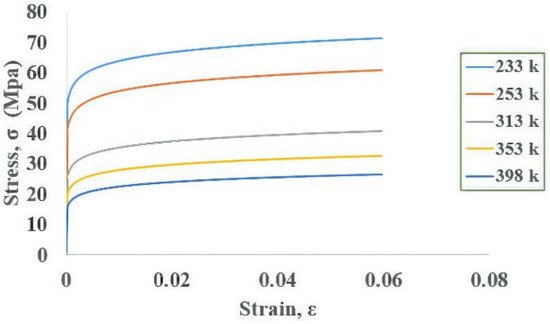
Materials 14 05342 g003 550
Figure 2. Stress–strain curve for SAC solder.
Electronics packaging geometry is usually symmetrical; therefore, in this study, half of the 2D structure was modeled along the diagonal, as shown in Figure 3. The X-direction displacement on each node was fixed to zero owing to the Y-symmetry. To prevent rigid body motion, the node at the lowest point of the neutral axis, which is at the printed circuit board (PCB), has all degrees of freedom fixed. The complete finite element model and the boundary conditions are shown in Figure 4. The thermal loading condition used in this research was JEDEC JESD22-A104D condition G [23], and the temperature range was −40 °C to 125 °C. The ramp rate was fixed at 16.5 °C/min and the dwell time was 10 min. In a qualified design, its mean-cycle-to-failure (MTTF) should pass 1000 thermal cycles. After the simulation process is completed, the incremental equivalent plastic strain in the critical zone is substituted into the strain-based Coffin–Manson model [24] for reliable life cycle prediction. For a fixed temperature ramp rate, this method is as accurate as the energy-based empirical equation [25][26] but with much less CPU time.
Materials 14 05342 g004 550
Figure 3. Symmetrical solder ball geometry.
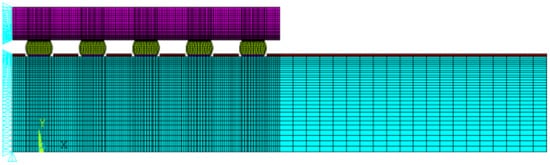
Materials 14 05342 g005 550
Figure 4. FEM model boundary condition.
The empirical formula for Coffin–Manson equivalent plastic strain model is shown in Equation (1):
Table 1 presents the predicted reliability life cycles of the WLP structure. The results show that the difference between the FEM-predicted life cycle and experiment result is within a small range. Therefore, experiments can be replaced by this validated FEM simulation to minimize the cost and time. Compared with the experiment approach, this validated FEM simulation procedure can provide large amounts of data within much less time and can be effectively used to generate a database for AI training.
Table 1. WLP finite element results for five test vehicles.
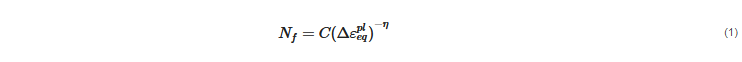
Test Vehicle Experimental
Reliability
(Cycles)		 Simulation
Reliability
(Cycles)		 Difference
TV1 318 313 −5
TV2 1013 982 −31
TV3 587 587 0
TV4 876 804 72
TV5 904 885 19

3. Machine Learning

3.1. Establishment of Dataset

The WLP structure consists of several components, including the solder mask, solder ball, I/O pad, stress buffer layer, and silicon chip, etc. (Figure 5). For illustration purposes, the four most influential parameters, namely silicon chip thickness, stress buffer layer thickness, upper pad diameters, and lower pad diameters, were selected to build the AI model and predict the reliability life cycles of new WLP structures. These four design parameters were used to generate both training and testing datasets for AI machine learning algorithms. Table 2 and Table 3 show the generated training dataset obtained through FEM simulation.
Materials 14 05342 g006 550
Figure 5. WLP geometry structure.

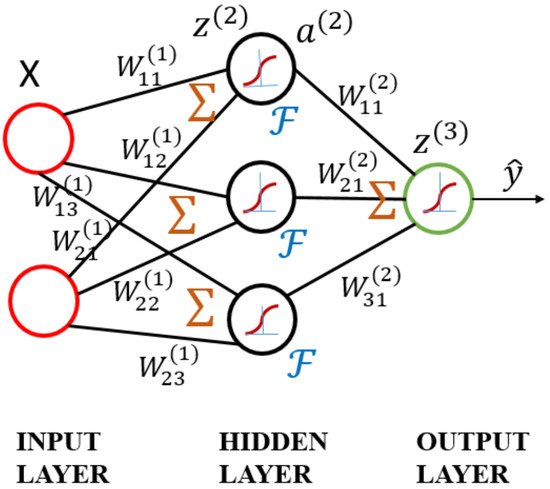
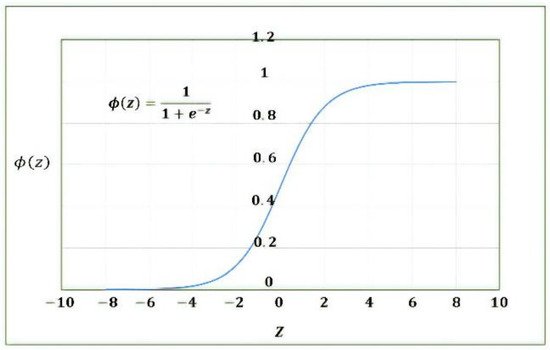
3.2. ANN Model

The ANN model is based on the concept of the brain’s self-learning ability, mimicking the human nervous system to process information. It is a multilayer neural network, as shown in Figure 6. The model consists of three layers: the input layer, where the data are provided; the hidden layer, where the input data are calculated; and the output layer, where the results are displayed [27]. As the numbers of neurons and hidden layers are increased, the ability to handle nonlinearity improves. However, these conditions may result in high computational complexity, overfitting, and poor predictive performance.
Materials 14 05342 g007 550
Figure 6. Schematic diagram of artificial neural network.
where the activation function is shown in Figure 7.
Materials 14 05342 g008 550
Figure 7. Sigmoid activation function.

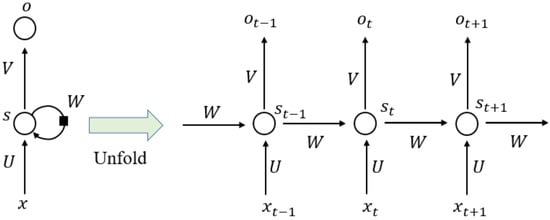
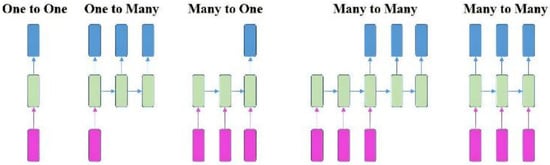
3.3. RNN Model

RNN is a type of neural network that can model “time-like”-series data, and it commonly adopts a nonlinear structure in deep learning. RNN [28][29] works on the principle that the output of a particular layer is fed back to the input layer to realize a time-dependent neural network and a dynamic model. Consequently, an ANN with nodes connected in a ring shape is obtained, as shown in the left half of Figure 8. The ring-shaped neural network is expanded along the “time” axis, as shown in the right half of Figure 8, where the “time” step t and the hidden state st can be expressed as a function of the output from the previous (st−1) “time” steps and previous layers (xt). U, V, and W denote the shared weights in RNN models during different “time” steps. Generally, the RNN series model can be divided into four types according to the number of inputs and outputs in given “time” steps; that is, one to one (O to O), one to many (O to M), many to one (M to O), and many to many (M to M). To synchronize the input features with the output results, RNN models can be subdivided into different series models, as shown in Figure 9 [30]. 
Materials 14 05342 g009 550
Figure 8. Schematic structure of recurrent neural network.
Materials 14 05342 g010 550
Figure 9. Different series model for RNN.

3.4. SVR Model

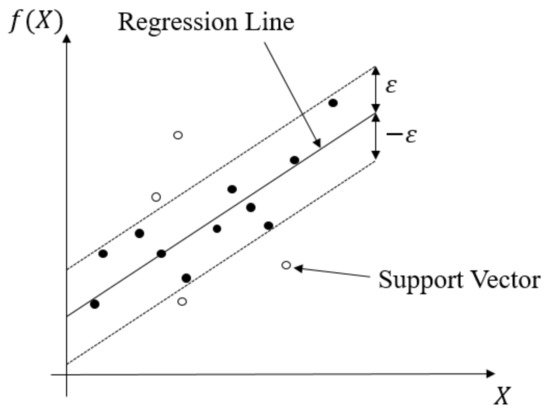
This regression method evolved from the support vector machine algorithm. It transforms data to high-dimensional feature space and adapts the ε-insensitive loss function (Equation (4)) to perform the linear regression in feature space (Equation (5)). In this regression method, the norm value of w is also minimized to avoid the overfitting problem. In other words, f(X,w), which is the function of the SVR model, will be as flat as possible. The SVR concept is illustrated in Figure 10. The data points outside the ε-insensitive zone are called support vectors, and two slack variables, ξi and ξ∗i, are used to record the loss of each support vector. Thus, the whole SVR problem can be seen as an optimization problem (Equation (6)). 

Materials 14 05342 g011 550
Figure 10. Schematic diagram of SVR.
In order to solve the optimization problem, the regression model is built as shown in Equation (7), where b is the bias of the SVR model.
In Equation (7), the term K(X,Xi) is known as the kernel function, and Xi is the training sample, with X as an input variable. This kernel function should be chosen as a dot product in the high-dimensional feature space [67]. There are numerous types of kernel functions. The commonly used kernel functions for SVR are the linear kernel, polynomial kernel, radial basis function (RBF) kernel, and sigmoid kernel.
All of the kernel functions satisfy Mercer’s condition; however, the regression results of the kernels vary. Therefore, it is essential to choose the best kernel function for the SVR algorithm to obtain optimal performance.

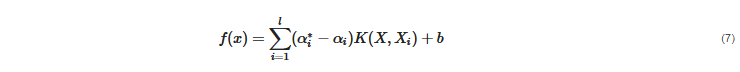
3.5. KRR Model

KRR combines ridge regression with the kernel “trick”. This model can learn a linear function in the space induced by the respective kernel and the dataset. Nonlinear functions in the original space can be used by the nonlinear kernels. The KRR algorithm also analyzes several kernels such as the RBF kernel, sigmoid kernel, and polynomial kernel to find the suitable kernel function for the WLP nonlinear dataset.

The KRR is possibly the most elementary algorithm that can be kernelized to ridge regression [31]. The classic method is used to minimize the quadratic cost, as shown in Equation (8). However, for the nonlinear dataset, the lower-dimensional feature space replaces the higher-dimensional feature space; that is, Xi→Φ(Xi). To convert lower-dimensional space to higher-dimensional space, the predictive model undergoes overfitting. Hence, to avoid overfitting, this function requires regularization. 

Hence, Equation (11) is very simple and more flexible due to introducing kernel function K, λ is the regularize factor with the identity matrix I, and y is the response variable. This model can also avoid both model complexity and computational time.

3.6. KNN Model

The KNN model is a statistical tool for estimating the value of an unknown point based on its nearest neighbors [69]. The nearest neighbors are usually calculated as the points with the shortest distance to the unknown point [70]. Several techniques are used to measure the distance between the neighbors. Two simple techniques are used in this study: the Euclidean distance function d(x,y), provided in Equation (12), and the Manhattan distance function d(x,y), provided in Equation (13).

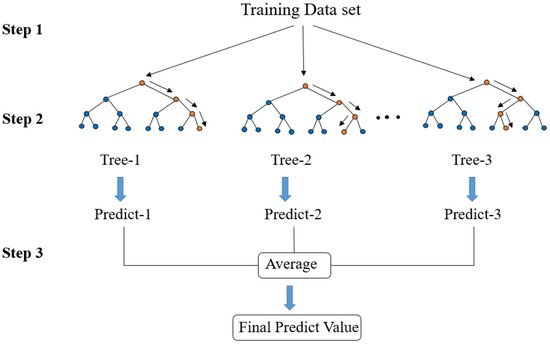
3.7. The RF Regression Model

RF is a collection of decision trees. These tree models usually consist of fully grown and unpruned CARTs.
The structure of the RF regression model is shown in Figure 10. This algorithm creates an RF by combining several decision trees built from the training dataset. The CART tree selects one feature from all of the input features as the segmentation condition according to the minimum mean square error method.
The RF algorithm procedure comprises three steps. In step 1, the bagging method is used to create a subset that accounts for approximately 2/3 of the total data volume. In step 2, if the data value is greater than the selected feature value, the data points are separated to the right from the parent node, otherwise to the left of the parent node (Figure 11). Afterward, a set of trained decision trees is created. In step 3, the RF calculates the average value of all decision tree results to obtain the final predicted value.
Materials 14 05342 g012 550
Figure 11. Schematic diagram of random forest structure.

3.8. Training Methodology

To obtain the best performance and avoid overfitting of the final trained regression model, several techniques, including data preprocessing (for standardization), cross-validation (for parameter selection), and grid search (for hyperparameter determination), were applied during training. The AI regression model was estimated using the method in the flowchart given in Figure 12.
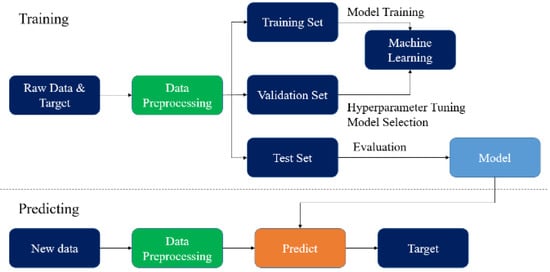
Materials 14 05342 g013 550
Figure 12. Methodology flow chart.

3.8.1. Data Preprocessing

The dataset values are not in a uniform range. Hence, before the machine learning model is developed, the data need to be preprocessed to standardize all of the input and output datasets and improve the modeling performance. Several data preprocessing methods, including min–max scaling, robust scaling, max absolute scaling, and standard scaling, were used in this study. Hence, of all preprocessing methods, we need to select the one method that provides the most accurately predicted output from the input dataset.

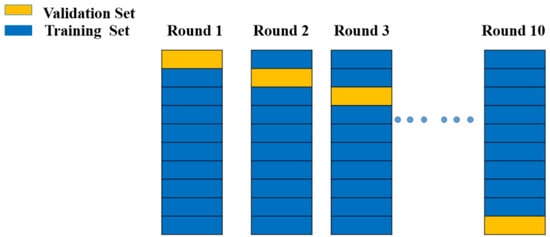
3.8.2. Cross-Validation

Cross-validation is the most frequently used parameter selection method. The basic idea of cross-validation is that not all of the dataset is used for training; a part of it (which does not participate in training) is used to test the parameters generated by the training set. The training data are trained with different model parameters and verified by the validation set to determine the most appropriate model parameters. Cross-validation methods can be divided into three categories: the hold-out method, k-fold method, and leave-one-out method. Owing to the huge calculation burdens of the hold-out method and the leave-one-out method, the k-fold method was chosen for this study (Figure 13). After the choice of data preprocessing method was confirmed, cross-validation was performed to avoid overfitting of the machine learning model, as shown in Figure 13. The dataset was divided into 10 parts, and each part acted as either a validation or training set in different training steps. The validation sets were also used to predict the training results.
Materials 14 05342 g014 550
Figure 13. Cross-validation model diagram from Round 1 to Round 10.

3.8.3. Grid Search Technique

Grid search is a large-scale method for finding the best hyperparameter to build the training model. In order to determine the best parameter, the search range value needs to be set by the model builder. Although the method is simple and easy to perform, it is time-consuming. Therefore, to reduce the computation time, this work adopted the grid search technique to find the best hyperparameter as compared to manually searching the hypermeter, and eventually, the training model was fixed with the above hyperparameters to run the best AI model.

This entry is adapted from the peer-reviewed paper 10.3390/ma14185342

References

  1. Andriani, Y.; Wang, X.; Seng, D.H.L.; Teo, S.L.; Liu, S.; Lau, B.L.; Zhang, X. Effect of Boron Nitride Nanosheets on Properties of a Commercial Epoxy Molding Compound Used in Fan-Out Wafer-Level Packaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 990–999.
  2. Cheng, H.-C.; Chung, C.-H.; Chen, W.-H. Die shift assessment of reconstituted wafer for fan-out wafer-level packaging. IEEE Trans. Device Mater. Reliab. 2020, 20, 136–145.
  3. Cheng, H.-C.; Wu, Z.-D.; Liu, Y.-C. Viscoelastic warpage modeling of fan-out wafer-level packaging during wafer-level mold cure process. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1240–1250.
  4. Dong, H.; Chen, J.; Hou, D.; Xiang, Y.; Hong, W. A low-loss fan-out wafer-level package with a novel redistribution layer pattern and its measurement methodology for millimeter-wave application. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1073–1078.
  5. Lau, J.H.; Li, M.; Li, Q.M.; Xu, I.; Chen, T.; Li, Z.; Tan, K.H.; Yong, Q.X.; Cheng, Z.; Wee, K.S. Design, materials, process, fabrication, and reliability of fan-out wafer-level packaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 991–1002.
  6. Lau, J.H.; Li, M.; Qingqian, M.L.; Chen, T.; Xu, I.; Yong, Q.X.; Cheng, Z.; Fan, N.; Kuah, E.; Li, Z. Fan-out wafer-level packaging for heterogeneous integration. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1544–1560.
  7. Lee, T.-K.; Xie, W.; Tsai, M.; Sheikh, M.D. Impact of Microstructure Evolution on the Long-Term Reliability of Wafer-Level Chip-Scale Package Sn–Ag–Cu Solder Interconnects. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1594–1603.
  8. Zhao, S.; Yu, D.; Zou, Y.; Yang, C.; Yang, X.; Xiao, Z.; Chen, P.; Qin, F. Integration of CMOS image sensor and microwell array using 3-D WLCSP technology for biodetector application. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 624–632.
  9. Chen, C.; Yu, D.; Wang, T.; Xiao, Z.; Wan, L. Warpage prediction and optimization for embedded silicon fan-out wafer-level packaging based on an extended theoretical model. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 845–853.
  10. Lau, J.H.; Ko, C.-T.; Tseng, T.-J.; Yang, K.-M.; Peng, T.C.-Y.; Xia, T.; Lin, P.B.; Lin, E.; Chang, L.; Liu, H.N. Panel-level chip-scale package with multiple diced wafers. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1110–1124.
  11. Lau, J.H.; Li, M.; Yang, L.; Li, M.; Xu, I.; Chen, T.; Chen, S.; Yong, Q.X.; Madhukumar, J.P.; Kai, W. Warpage measurements and characterizations of fan-out wafer-level packaging with large chips and multiple redistributed layers. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1729–1737.
  12. Qin, C.; Li, Y.; Mao, H. Effect of Different PBO-Based RDL Structures on Chip-Package Interaction Reliability of Wafer Level Package. IEEE Trans. Device Mater. Reliab. 2020, 20, 524–529.
  13. Qin, F.; Zhao, S.; Dai, Y.; Yang, M.; Xiang, M.; Yu, D. Study of warpage evolution and control for six-side molded WLCSP in different packaging processes. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 730–738.
  14. Wang, P.-H.; Huang, Y.-W.; Chiang, K.-N. Reliability Evaluation of Fan-Out Type 3D Packaging-On-Packaging. Micromachines 2021, 12, 295.
  15. Yang, C.; Su, Y.; Liang, S.Y.; Chiang, K. Simulation of wire bonding process using explicit FEM with ALE remeshing technology. J. Mech. 2020, 36, 47–54.
  16. Liu, C.-M.; Lee, C.-C.; Chiang, K.-N. Enhancing the reliability of wafer level packaging by using solder joints layout design. IEEE Trans. Compon. Packag. Technol. 2006, 29, 877–885.
  17. Chiang, K.-N.; Chen, W.-H.; Cheng, H.-C. Large-scale three-dimensional area array electronic packaging analysis. J. Comput. Model. Simul. Eng. 1999, 4, 4–11.
  18. Tsou, C.; Chang, T.; Wu, K.; Wu, P.; Chiang, K. Reliability assessment using modified energy based model for WLCSP solder joints. In Proceedings of the International Conference on Electronics Packaging (ICEP), Yamagata, Japan, 19–22 April 2017; pp. 7–15.
  19. Liu, S.; Panigrahy, S.; Chiang, K. Prediction of fan-out panel level warpage using neural network model with edge detection enhancement. In Proceedings of the IEEE 70th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3–30 June 2020; pp. 1626–1631.
  20. Yuan, C.C.; Lee, C.-C. Solder joint reliability modeling by sequential artificial neural network for glass wafer level chip scale package. IEEE Access 2020, 8, 143494–143501.
  21. Ramalho, L.; Belinha, J.; Campilho, R. A new crack propagation algorithm combined with the finite element method. J. Mech. 2020, 36, 405–422.
  22. Chang, J.; Wang, L.; Dirk, J.; Xie, X. Finite element modeling predicts the effects of voids on thermal shock reliability and thermal resistance of power device. Weld. J. 2006, 85, 63s–70s.
  23. JEDEC Solid State Technology Association. JEDEC Standard JESD22-A104D, Temperature Cycling. Jedec. Org 2005, 11, 2009.
  24. Coffin, L.F., Jr. A study of the effects of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–950.
  25. Ramachandran, V.; Wu, K.; Chiang, K. Overview study of solder joint reliablity due to creep deformation. J. Mech. 2018, 34, 637–643.
  26. Lee, C.-H.; Wu, K.-C.; Chiang, K.-N. A novel acceleration-factor equation for packaging-solder joint reliability assessment at different thermal cyclic loading rates. J. Mech. 2017, 33, 35–40.
  27. Chou, P.; Chiang, K.; Liang, S.Y. Reliability assessment of wafer level package using artificial neural network regression model. J. Mech. 2019, 35, 829–837.
  28. Tang, Z.; Fishwick, P.A. Feedforward neural nets as models for time series forecasting. ORSA J. Comput. 1993, 5, 374–385.
  29. Zhang, D.; Han, X.; Deng, C. Review on the research and practice of deep learning and reinforcement learning in smart grids. CSEE J. Power Energy Syst. 2018, 4, 362–370.
  30. Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471.
  31. Welling, M.; Kernel Ridge Regression. Max Welling’s Class Notes in Machine Learning. 2013. Available online: https://web2.qatar.cmu.edu/~gdicaro/10315/additional/welling-notes-on-kernel-ridge.pdf (accessed on 6 August 2021).
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Feedback