1. Introduction
Darcy’s Law [1], which was obtained through laboratory seepage column experiments by Darcy in 1856, is an important milestone in the history of hydrogeology and has led to the transition of hydrogeology from qualitative descriptions to quantitative calculations. Seven years later, Dupuit established the Dupuit stable well flow model (also known as the round island model) based on Darcy’s Law and derived the stable well flow formula known as the Dupuit formula [2]. In the Dupuit model, the aquifer is a finite volume cylinder placed in the sea, and the pumping well is located at the axis of the cylinder, which is an ideal model for high generalization. In reality, aquifers with a finite cylinder shape, constant head boundary at the side, and zero flux boundaries at the top and bottom are extremely rare, and actual aquifers are also difficult to generalize as assumed by the Dupuit model and calculated directly using the Dupuit formula. Consequently, the practical application of the Dupuit model has been largely limited since its inception. To solve this problem, Thiem [3] extended the Dupuit model to a horizontal infinite aquifer using an approximate hypothesis and thus established the Thiem model. This model has a parameter called the range of cone of depression. Thiem assumed that this parameter represents the horizontal distance from the pumping well to the point where the water level cannot actually be observed to drop; therefore, a large error will not occur in the replacement of the round island radius “R” with the parameter of the range of cone of depression [4]. Later, Todd [5] figuratively renamed the range of the cone of depression as the influence radius and argued that it was not necessarily observable, but rather an approximate empirical value [6], which is how the influence radius originated.
The influence radius may be confusing with regard to the Dupuit model and Thiem model, and it is believed that the round island radius (R) in the former is equivalent to the influence radius (R) in the latter. Additionally, it is believed that the influence radius is objective, immutable, and measurable [7], and has nothing to do with human impact, in a manner similar to some hydrogeological parameters such as the hydraulic conductivity, specific yield, and round island radius. This erroneous understanding has misled practical work and resulted to errors in the theories and methods of groundwater resource evaluation [8]. Thus, the development of groundwater resources and the prevention and control of groundwater pollution have been subject to misleading information. This is particularly the case for the division of groundwater source protection areas [6]. In recent years, the influence radius has occasionally been discussed in academia [9][10][11], but consensus has not been reached. Considering this situation in combination with the needs of theoretical research and practical application, this paper tries to use non-professional language to further discuss the issue of the influence radius through mathematical reasoning and analogy to clarify this issue.
2. Birth and Application History of Influence Radius
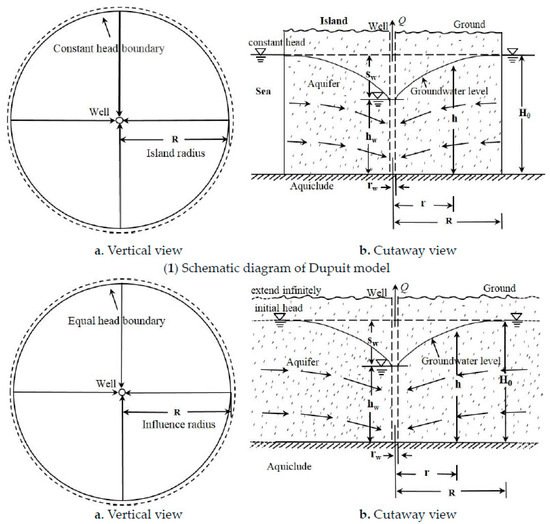
Dupuit made the following assumptions when he established the stable well flow model (round island model for short, Figure 1 (1): the unconfined aquifer is a homogeneous and isotropic circular island aquifer with a horizontal lower confining bed, the lateral boundary of the well has a constant head and there is a completely penetrating well in the center of the aquifer, the aquifer does not have vertical infiltration recharge and evaporation, and the seepage is a steady flow that conforms to the linear law.
Figure 1. Schematic diagram of Dupuit model and Thiem model. Q is the water yield of the pumping well, [L3T−1]; sw is the drawdown of the pumping well, [L]; h is the groundwater level at distance r from the pumping well, [L]; H0 is the thickness of the aquifer, [L]; hw is the water level of the pumping well, [L]; rw is the radius of the pumping well, [L]; r is the distance between the pumping well and observation well, [L]; and R is the influence radius, [L].
Although the Thiem model was established based on the Dupuit model, there are essential differences between them. First, the aquifer in the Dupuit model is cylindrical and has a well-defined boundary, which is surrounded by water. The Dupuit formula does not work without this boundary, while the aquifer in the Thiem model extends indefinitely in the horizontal direction and does not have a boundary. Thus, there are essential differences with regard to the assumed boundary conditions. Additionally, in the Dupuit model, R refers to the radius of the cylindrical aquifer and is a geometric parameter describing the volume of an object. Moreover, R has a fixed value, which means that the cylindrical aquifer has a fixed volume. In the Thiem model, R refers to the horizontal distance from the center of the pumping well to the point at which the drawdown of the groundwater level is virtually unobservable; therefore, it is not a geometric parameter. The values of R in different directions of the aquifer may also be different because of the heterogeneity of the aquifer, and the boundary of the cone of depression in an aquifer may not be a circle [4][12]. Additionally, in the Dupuit model, the exterior of the cylindrical aquifer is full of water, and the aquifer can receive a constant supply of water. After pumping in the aquifer for a certain period of time, the water yield of the aquifer is entirely supplied by recharge from the outside of the boundary and the water is inexhaustible. Thus, a steady flow can form in the aquifer. In the Thiem model, the range beyond which R is involved is still an aquifer. When water is pumped in a horizontal infinite aquifer without leakage and external recharge, all of the water yield comes from the consumption of internal storage in the aquifer. Thus, it is impossible to form a stable flow in the aquifer [13]. Additionally, if water is pumped for a certain period of time, the water level in the pumping well will drop to the lower confining bed.
Based on the Dupuit model and Thiem model, studies have successively deduced various formulas for calculating the influence radius according to their own understanding ( Table 1 ). Some of these formulas are semi-empirical [14] and do not only involve hydrogeological parameters, such as K, H 0, and μ, but also time factors. This indicates that some studies have realized that the influence radius is not a fixed hydrogeological parameter, but instead changes with time. The others are empirical formulas [14], which not only contain hydrogeological parameters but also include pumping variables such as s w and Q in the calculation of the influence radius. These formulas only consider one of the time variables and pumping condition variables, and some even consider the influence radius as a given hydrogeological parameter [14].
Table 1. Equations for calculating the influence radius.
| Equation Name |
Equation |
Application Condition |
Author, Year |
Parameter |
| Weber equation |
R=746KH0tμ−−−−−√ |
| |
Unconfined aquifer |
Schultze, 1924 |
R: influence radius, [L]; K: hydraulic conductivity, [LT−1]; H0: thickness of aquifer, [L]; t: time from beginning of pumping to formation of stable cone of depression of groundwater level, [T]; μ: specific yield; sw: drawdown of pumping well, [L]; Q: water yield of pumping well, [L3T−1]; I: hydraulic gradient of groundwater level |
| Kusakin equation |
R=2swH0K−−−−√ |
| |
Unconfined or confined aquifer |
Chertousov, 1949 |
| R=476KH0tμ−−−−−√ |
| |
Unconfined aquifer |
Aravin and Numerov, 1953 |
| Siechardt equation |
R=10swK−−√ |
| |
Preliminary stage of pumping in unconfined or confined aquifer |
Chertousov, 1962 |
| Wilbur equation |
R=3KH0tμ−−−−√ |
| |
Unconfined aquifer |
Chen, 1976 |
| Kelgay equation |
R=Q2KH0I |
| |
Completely penetrating well in unconfined aquifer |
Chen, 1976 |
To facilitate calculation, some people have introduced the influence radius into some well flow calculation formulas for the forward calculation of variables such as the water level and flow rate, or for the inversion of hydrogeological parameters such as the hydraulic conductivity and water storage coefficient ( Table 2 ).
Table 2. Analytic solution models and equations using the influence radius.
| Model/Equation Name |
Equations Group |
Application Condition |
Author, Year |
Parameter |
| Forward model/equation |
R: influence radius, [L]; K: hydraulic conductivity, [LT−1]; H0: thickness of aquifer, [L]; t: time from beginning of pumping to formation of stable cone of depression of groundwater level, [T]; μ: specific yield; sw: drawdown of pumping well, [L]; Q: water yield of pumping well, [L3T−1]; I: hydraulic gradient of groundwater level. |
| Plotnikov equation |
Q=eQ02RB |
| |
Well group pumping |
Chen et al., 1976 |
| Dupuit–Forchheimer equation |
h2=H20−QπKlnRrw |
| |
Unconfined aquifer |
Poehls and Smith, 2009 |
| sw-calculate equation |
Q=2πTswlnRrw |
| |
Confined aquifer |
China Geological Survey, 2012 |
| Inversion model/equation |
| Siechardt equation |
T=Q2πswlnRrw |
| |
Confined aquifer |
China Geological Survey, 2012 |
| Wilbur equation |
K=Qπ[H20−(H0−sw)2]lnRrw |
3. Gap between Theory and Practice
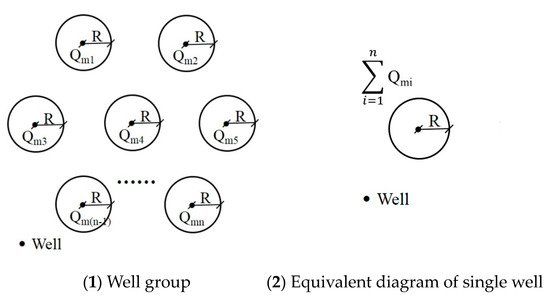
However, many studies have reported that the influence radius R is a hydrogeological parameter reflecting the natural properties of aquifers, similar to parameters such as the porosity n, specific yield μ, and hydraulic conductivity K. Therefore, the influence radius is a constant value that is not affected by the drawdown s w and water yield Q [15]. Studies have given the empirical values of R for aquifers with different particle structures ( Table 3 ) and have considered that greater aquifer permeability—that is, larger aquifer particles—results in a larger R value. When pumping water in an aquifer without external recharge, the cone of depression will expand with the increase of the water yield and the advancement of time. If the empirical influence radius value is used, such as in the case of the coarse gravel aquifers mentioned in some papers, the empirical value of the influence radius will be 1500–3000 m ( Table 3 ). In other words, regardless of how large the amount of exploitation is and how long the exploitation period is, the cone of depression of the aquifer will not continue to expand outward after extending to 1500–3000 m. Accordingly, it is assumed that, in a certain pumping well group in an aquifer, the water yield of n single pumping wells is Q m1 , Q m2 ,…, Q mn , respectively , their influence radius is R ( Figure 2 (1)), and a regional cone of depression will be formed. If the sum of the water yield of n single wells in the well group is provided by a single well, then a cone of depression with an influence radius R will be formed ( Figure 2 (2)). In this case, owing to the decrease in the number of wells, the area affected by pumping will be much smaller compared with when the well group is pumped. However, without external recharge, this phenomenon is completely impossible in an aquifer; otherwise, the aquifer will become an inexhaustible resource, which is contrary to common sense.
Table 3. Empirical relationship of K and R.
| K (m/d) |
R (m) |
| 0.5–1 |
25–50 |
| 1–5 |
50–100 |
| 5–20 |
100–300 |
| 20–50 |
300–400 |
| 50–100 |
400–500 |
| 75–150 |
500–600 |
| 100–200 |
600–1500 |
| 200–500 |
1500–3000 |
This table is taken from
[16]; K is the hydraulic conductivity, [LT
−1]; and R is the influence radius, [L].
Figure 2. Influence radius in well group pumping and single well pumping in influence radius theory. R is the influence radius, [L]; Qmi is the maximum water yield of pumping well i, [L3T−1]; and n is the number of pumping wells.
The seemingly stable phenomenon observed in practice known as the quasi-steady state [14] is essentially different from the influence radius considered in theory. The term “seemingly stable” means that, when pumping the water in an aquifer, the change of the groundwater piezometric head close to the well gradually slows down as the pumping time increases. Thus, within a certain range, it is close to a stable state and has the same shape as the falling curve of stable flow [16]. For a long time, the seemingly stable phenomenon observed in practice was associated with the theoretical influence radius, and the influence radius has even been used to represent the influence range when the aquifer is in a seemingly stable state. This confirms the rationality of the influence radius parameter, which is a misunderstanding of the seemingly stable phenomenon and influence radius concept.
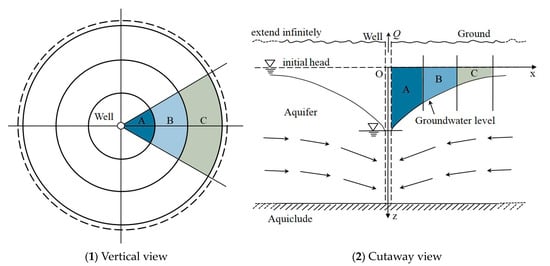
The stable or seemingly stable groundwater level observed in practice is simply a coincidence that occurs under the influence of various practical factors and a misapprehension caused by the low accuracy of the actual measurement of the groundwater level or by the recharge of the aquifer. Therefore, this phenomenon cannot be used to explain the rationality of the influence radius parameter in theoretical models. The steady state does not exist under pumping conditions without recharge in theory. According to the continuity principle of fluids, in the cone of depression generated by pumping water, the amounts of water passing through regions A, B, and C in a unit of time are equal. However, from region A to region C, the basal area gradually increases ( Figure 3 (1)); therefore, the height gradually decreases ( Figure 3 (2)). Similarly, the drawdown at infinity will be very small but not zero, because the water yield is a concept of volume and cannot be changed from three dimensions to two dimensions. The location of the pumping well is considered as the origin of the coordinates to establish the coordinate system, and the drawdown s w is considered as a function of x, namely z = s w (x). When pumping water, the drawdown of the aquifer is larger when the distance to the pumping well is shorter. As x approaches ∞, the drawdown tends towards zero ( Figure 3 ). Assuming that the radius of the pumping well is r w = 0, then the water yield of the pumping well is the volume of the rotating body obtained by rotating the curvilinear trapezoid bounded by a continuous curve z = s w (x) , z -axis, line x = +∞, and line z = 0 once around the z -axis. For convenience of description, the object of investigation was considered to be a unit width aquifer passing through the axis; then, the value of its volume is V = ∫ s w ( x ) d x ,( 0, ∞ ) . When water is pumped continuously, x tends towards ∞; therefore, V also tends towards ∞. This means that the cone of depression will expand infinitely; therefore, a stable state cannot be formed. What is commonly referred to as the seemingly stable state does not mean that the groundwater level is stable, but that the change of the water level cannot be observed, which thus gives the illusion of stability. The phenomenon whereby the change of the water level cannot be observed is caused by the means of observation and other factors (external recharge). This is similar to the detection limit in analytical chemistry, which is a relative concept. With the improvement of the observation means, the observed drawdown range of the water level will increase. Therefore, the influence radius R cannot be considered as an intrinsic parameter of the aquifer beyond which there is no drawdown of the water level.
Figure 3. Formation of cone of depression of groundwater level during pumping. Q is the water yield of the pumping well, [L3T−1].
Therefore, in theory, the influence range will continue to expand with the extension of pumping time in an infinite aquifer without external recharge. However, there are big differences between reality and theory: (1) in reality, there are no unbounded aquifers that extend indefinitely in the horizontal direction. Therefore, for an aquifer without external recharge, the boundary of the influence range is the boundary of the aquifer when the pumping time is sufficiently long. (2) In reality, there are few aquifers without external recharge. The phenomenon whereby the observed water level reaches a stable or quasi-stable state when pumping in reality is attributed to the measurement accuracy [17]. More importantly, this phenomenon is attributed to the fact that the aquifer may have obtained unknown external recharge, such as atmospheric precipitation, surface water, and agricultural irrigation water [18], as well as to the vertical leakage recharge caused by pumping [19]. This contradicts the assumption of a lack of external recharge in the theoretical model, which is often ignored and thus results in the illusion of water level stability. Coincidences that occur in practical situations have led to the false impression that the influence radius theory has been verified, which has resulted in the wide adoption of the theory and consequently to the excessive exploitation of groundwater resources. Thus, the improved Dupuit model, which introduces external recharge, is more in line with actual needs [20].
This entry is adapted from the peer-reviewed paper 10.3390/w13152050