Bus Operations Scheduling Subject to Resource Constraints Using Evolutionary Optimization: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Transportation
Contributor:
Konstantinos Gkiotsalitis

In public transport operations, vehicles tend to bunch together due to the instability of passenger demand and traffic conditions. Fluctuation of the expected waiting times of passengers at bus stops due to bus bunching is perceived as service unreliability and degrades the overall quality of service. For assessing the performance of high-frequency bus services, transportation authorities monitor the daily operations via Transit Management Systems (TMS) that collect vehicle positioning information in near real-time. This work explores the potential of using Automated Vehicle Location (AVL) data from the running vehicles for generating bus schedules that improve the service reliability and conform to various regulatory constraints. The computer-aided generation of optimal bus schedules is a tedious task due to the nonlinear and multi-variable nature of the bus scheduling problem. For this reason, this work develops a two-level approach where (i) the regulatory constraints are satisfied and (ii) the waiting times of passengers are optimized with the introduction of an evolutionary algorithm. This work also discusses the experimental results from the implementation of such an approach in a bi-directional bus line operated by a major bus operator in northern Europe.

  • bus bunching
  • evolutionary optimization
  • constrained optimization
  • service reliability

Introduction

During the scheduling phase of bus services, a set of conflicting objectives are optimized such as the operational costs and the waiting times of passengers at stops. However, due to many exogenous factors, such as road traffic and spatio-temporal passenger demand variations, the optimal schedule does not perform as anticipated, resulting in bus bunching phenomena. This unreliability leads to passenger dissatisfaction and to additional operational costs for the service provider. Therefore, several research works related to bus bunching have tried to address the service reliability problem (Gkiotsalitis and Cats [1], Chapman and Michel [2], Pilachowski [3], Gkiotsalitis and Maslekar [4]).
 
In several cities where the timetables of bus services are not strictly followed, a number of informal methods have been utilized for maintaining the service reliability. In Chile for instance, drivers are assisted by an informal group of independent information intermediaries, known as “Sapos”, who record the arrival time of buses and inform the subsequent drivers in order to help them maintain uniform headways (Johnson et al. [5]). These labor-intensive practices of maintaining reliability in bus operations become inefficient when the frequency of trips is very high. This study focuses specifically on such high frequency services with dispatching headways between consecutive bus trips of less than 15 min since several studies (Randall et al. [6], Welding [7]) have shown that the arrivals of passengers at stops are not random and are tailored to the scheduled arrival times of bus trips in the case of low frequency services.
 
The advent of new monitoring technologies such as in-vehicle telematics and automated fare collection systems has revolutionized the monitoring capabilities of the transit service operations. Nowadays, the monitoring capabilities of the passenger waiting times at stops have been increased and, given this new information, bus operators strive to improve the reliability of their daily operations.
In past years, several methodologies were developed for enhancing the reliability of transit services. Eberlein [8] explained three ways of controlling the headways: (a) Station-control strategies which consist of (i) holding a bus at a stop and (ii) stop-skipping; (b) Interstation-control strategies consisting of speed control and traffic signal priorities and (c) On-demand vehicle addition strategies that add vehicles at some specific points of the bus routes. From the above-mentioned strategies, the first strategy that includes holding and stop skipping is considered to be the most important methodology.
 
To further explain the bus holding control strategy, a bus trip can be held at specific critical stops (known as control points or time points) in an effort to maintain even headways. In several works, such as the work of Hickman [9], bus holding is proposed as a real-time strategy to avoid bus bunching. The typical objective of a bus holding strategy is to ensure that the waiting times of passengers at stops do not vary significantly from the planned ones. However, recent works, such as the work of Bartholdi and Eisenstein [10], focused on maintaining even headways between bus trips at the locations of the control point stops without adhering to the planned headway values. Although bus holding can be proved beneficial to bus operations, several works have proposed to introduce limitations on holding strategies because extensive holding of bus trips can cause inconvenience to passengers, overcrowding at stops and “schedule sliding” if the bus trips are postponed due to holding (Delgado et al. [11]).
 
Public transport authorities use the passenger waiting times at stops to evaluate the performance of the operations in the case of high frequency services. In contrast to the low frequency services where the main objective is the service punctuality because passengers try to synchronize their arrival times at stops with the scheduled arrival times of bus trips, in high frequency services the passenger arrival times at stops are random (Welding [7]) and the waiting times of passengers at stops can be directly linked to the headways between consecutive trips (they are considered equal to half the value of the headways). O’Flaherty and Mancan [12] studied the relationship between bus headways and average passenger waiting times in peak and off-peak traffic conditions. The holding problem has been examined as a multi-objective problem in other works such as Barnett [13], where a holding strategy of individual buses at control stops tries to minimize at the same time the passenger waiting times and the delay of on-board passengers. Turnquist [14] studied in more detail the effects of schedule reliability and bus frequency on the waiting times experienced by the passengers. In addition, the stochastic nature of passenger waiting times was considered in the work of Gkiotsalitis and Maslekar [15], where a stochastic search and branch hopping/merging algorithm was used for reducing the excess waiting times of passengers.
 
Apart from bus holding, a variety of other solution strategies have been proposed for improving the bus operations. Adherence to the planned timetables was proposed by Bates et al. [16] and Daganzo [17] where the latter worked on an adaptive control scheme that focused on achieving target headways by adjusting the bus cruising speed. In such a scheme, when a bus arrives at a control point its headway is compared to a pre-specified target headway value for performing the appropriate adjustment. Other works, such as Friedman [18], have focused only on the dispatching times of bus trips by developing mathematical models to optimize the departure times of buses.
 
The above-mentioned works focus on specific problems such as the (i) timetable design and the (ii) real-time control. This paper focuses on the first problem of timetable design for high frequency services with a specific target of reducing the passenger waiting time fluctuations and satisfying the resource limitations in terms of fleet size and regulatory constraints. Regulatory constraints such as bus driver meal breaks, layover times and dispatching headway bounds are interconnected and any change in the bus timetables can lead to violations of different constraints. Satisfying the regulatory constraints and minimizing the Excess Waiting Times (EWT) of passengers at control point stops turns the timetabling problem into a discrete, constrained optimization problem which does not exhibit a polynomial computational complexity. For this reason, this paper presents an evolutionary algorithm for exploring the vast solution space under a set of constraint limitations. The performance of the proposed algorithm, the improvement in the timetable design and the improvement of passengers waiting times at stops in real operations under different assumptions of travel time variations are tested in a bi-directional bus line from a major bus operator in northern Europe.

Related Work

Yan and Chen [19] developed a model for timetable design by formulating the movement of bus trips and the passenger flows in order to manage the interrelationship between passenger demand and bus trip supply. They formulated the problem as a mixed integer multiple commodity network flow problem and a Lagrangian heuristic algorithm was developed for solving it.
 
Niu and Tian [20] developed a methodology to determine the dispatching times of bus trips subject to capacity constraints with the use of heuristic algorithms. This methodology was based on the concept that a constant headway cannot satisfy effectively the time-dependent passenger demand. In contrary, an irregular schedule that allows uneven headways might be able to accommodate the dynamic demand patterns. The operational time was divided into various equal time periods to formulate the transit scheduling problem. Considering the dwell times and the trip travel times, the dispatching time of each bus trip was calculated subject to inequality constraints that belong to the specific operational time period. The objectives were the reduction of passenger waiting times and the reduction of the number of vehicles leading to a bi-objective function which is also adopted by other works such as Gkiotsalitis and Cats [21] and Ceder et al. [22]. In particular, Ceder et al. [22] followed this bi-objective optimization approach for minimizing headway deviations and passenger loads at the same time using a graphical heuristic approach.
 
Sun et al. [23] explored the idea of using a flexible timetable optimization based on hybrid vehicle sizes in order to address the travel demand fluctuations. This study compared operational strategies like total travel times and total costs of using large size or smaller size buses at different time periods such as peak and off-peak periods. Following this approach, the total in-vehicle time cost and the waiting time cost at stops were considered. In addition, an optimization model considering hybrid, large and smaller-size vehicles was solved with the use of an adaptive heuristic algorithm. From the results, it was observed that a hybrid bus schedule providing the benefits of both large and smaller size vehicles can be implemented for reducing the operational costs and managing the passenger demand more efficiently. Nevertheless, limitations in resources such as the availability of different bus types might restrict the applicability of such a method in practical problems.
 
Chen [24] defined a timetable setting problem to determine the dispatching time of bus trips based on the flow intensity of passengers. This method minimized the total waiting time of passengers at stops by determining the number of bus trips for each time period and the dispatching times of these trips using dynamic optimization. Using dynamic programming, the arrangements of bus trips were designed as a multi-stage optimization problem which was optimized by finding the global optimal solution. The dispatching times of bus trips were computed by considering the passenger flow intensity, the available resources and the operational costs for each optimization time period.
 
More recently, Gkiotsalitis and Stathopoulos [25] developed a method for modifying the dispatching times of trips in order to reduce the waiting time deviation of passengers at stops and synchronize the arrival times of buses at specific stops with the starting times of activities (i.e., major events that can be derived from social media data (Gkiotsalitis and Stathopoulos [26])). This multi-objective optimization was treated as a single-objective optimization problem with the use of weight factors for each one of the main objectives.
 
Other works related to timetable design for railway services, such as Shi et al. [27], utilized also the minimization of passenger waiting times as the main problem objective. The focus of such works was on loop-shaped lines that connect several radial lines together; thereby, enhancing the accessibility of the rail network. For enhancing the accessibility of the rail network, Shi et al. [27] formulated a bi-objective function considering the waiting times at the stops of the line together with the waiting times related to passenger transfers subject to constraints such as total trip times, departure times, headways to be maintained, arrival times and dwell times. This formulation resulted in a nonlinear programming problem which was also non-convex. Hence a genetic algorithm was applied and was effective in reducing the passenger waiting times. However, the optimization during off-peak periods was more effective than the peak periods due to the shorter headways that are exhibited during the peak periods.
 
It is also worth noting that several other works from the field of logistics (i.e., Cattaruzza et al. [28], Du et al. [29]) focus on developing daily schedules for deliveries with the objective of reducing the operational costs while satisfying all delivery requests. Nevertheless, a distinct difference between the delivery scheduling problems and the transit timetabling problems is the inclusion of multiple vehicle routing sub-problems in the scheduling phase of the former.
 
The majority of the previous timetable optimization approaches have developed methodologies to optimize passenger waiting times without an in-depth consideration of the resource limitations of the transit service providers. For instance, many times it is impractical to introduce new trips in a route in order to meet the passenger demand fluctuations given the inherent resource limitations. This paper explores this area by including resource constraints such as driver meal and resting times in the problem definition and developing a Genetic Algorithm (GA) to optimize the resulting objective function as it is presented in the next sections.
 

Results and Concluding Remarks

This study focused on the timetabling problem with the objective of reducing the excess waiting times of passengers at control point stops while satisfying the regulatory constraints. This study utilized information from telematic systems that monitor the daily operations for estimating the travel times between control point stops at different times of the day and computing timetables that can improve the service reliability.
In order to compute the timetables with the use of historical AVL data, the timetabling problem was formulated as a discrete, non-convex and multi-constrained optimization problem. For this reason, a problem-specific GA was developed that updated dynamically the exchange of genes between population members during the crossover phase in order to generate more fit offsprings. This solution method was applied in a bi-directional bus line in north Europe producing a timetable that satisfied all regulatory constraints for an excess waiting time of passengers at the level of 0.298 min as it is presented in Figure 1 and Figure 2.
 
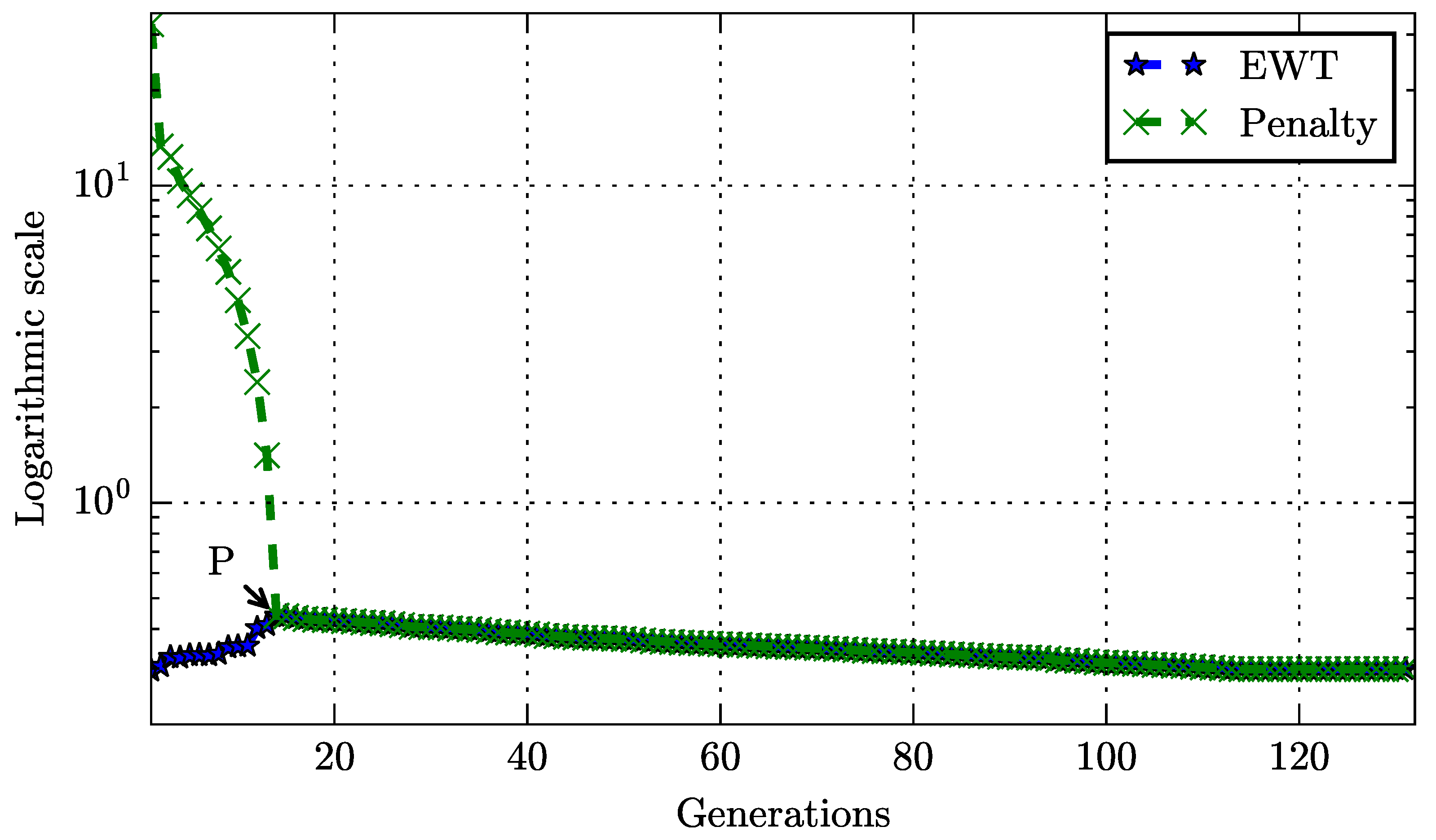
Penalty function reduction at every iteration of the GA.
Figure 1. Penalty function reduction at every iteration of the GA.
 
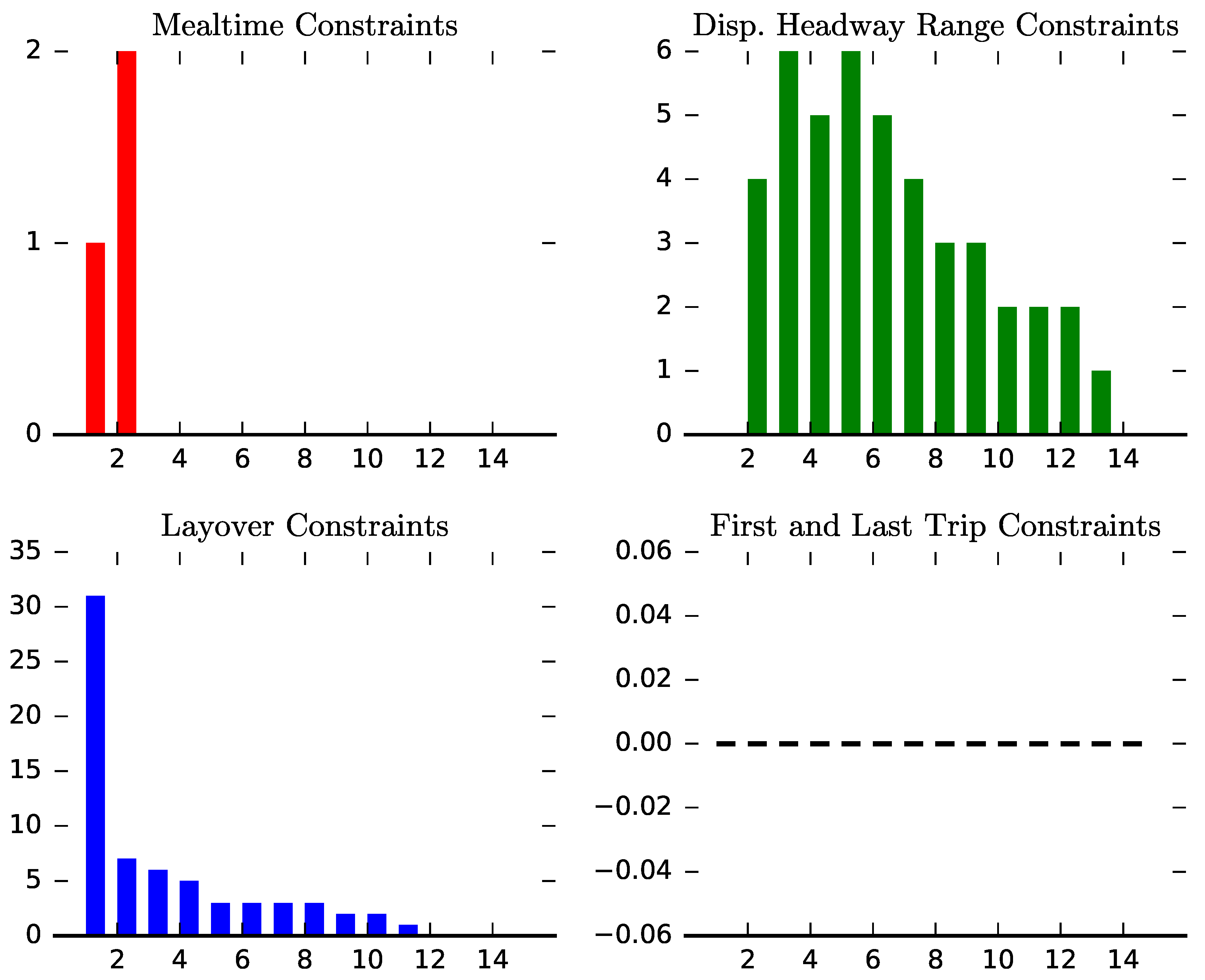
Variation of constraints with every generation.
Figure 2. Variation of constraints with every generation.
 
From the analysis, it was observed that:
  • All violated constraints were satisfied after a number of population evolutions;
  • During the satisfaction of violated constraints, the EWTs of passengers were negatively impacted and were increased by 30%;
  • After the satisfaction of constraints, the EWTs of passengers were improved leading to a 0.298-min service-wide EWT.
The EWT value of the optimized timetable will occur in practice if the actual travel times of buses are equal to the estimated ones. However, this is not the case in real-world operations. For instance, well-controlled services with planned timetables that have EWT values close to zero exhibit daily EWTs of 0.8 to 2 min (TfL [39]) in real-world operations. Due to that, this work investigated the impact of the fluctuations of the actual travel times to the EWTs of passengers. In principal, even the smallest travel time fluctuation has the ability to increase the ideal service-wide EWT of 0.298 min of our optimal timetable. For this reason, a simulation-based validation was performed where travel times were allowed to vary from their expected values for 10%, 20%, …, 80%. In this analysis, the service-wide EWT showed resilience for travel time variations of up to 50% but after that point the EWTs and constraint violations were increased in a disproportionate manner. This is a key finding that underlines the importance of addressing exogenous factors such as road traffic and/or road works for maintaining the reliability of the running services.
In future work, the timetabling optimization, which focused on satisfying the regulatory constraints, using AVL-data insights for estimating the travel times, can be expanded even further for improving the excess waiting times of passengers at transfer stops in order to increase the reliability of multi-modal trips. In addition, the stochastic nature of the travel times can be incorporated in the objective function of the timetabling optimization resulting in a stochastic optimization problem with the use of supervised learning methods or by fitting the observed travel times from the archived AVL data to probability distributions. In this way, the reliability improvement potential of stochastically optimized timetables can be further examined. Finally, it is worth examining the potential improvement of the proposed GA convergence rate during the timetabling optimization after incorporating in it advanced hybridization techniques that are described in recent works related to forecasting problems (such as the work of Lopez-Garcia et al. [40] on predicting the short-term travel times in highways).
 

Abbreviations

The following abbreviations are used in this manuscript:
AVL Automated Vehicle Location
EA Evolutionary Algorithm
EWT Excess Waiting Time
GA Genetic Algorithm
TMS Transit Management Systems
TT Travel Time

References

  1. Gkiotsalitis, K.; Cats, O. Reliable frequency determination: Incorporating information on service uncertainty when setting dispatching headways. Transp. Res. Part C Emerg. Technol. 2018, 88, 187–207. [Google Scholar] [CrossRef]
  2. Chapman, R.; Michel, J. Modelling the tendency of buses to form pairs. Transp. Sci. 1978, 12, 165–175. [Google Scholar] [CrossRef]
  3. Pilachowski, J.M. An Approach to Reducing Bus Bunching; University of California: Berkeley, CA, USA, 2009. [Google Scholar]
  4. Gkiotsalitis, K.; Maslekar, N. Dynamic Bus Operations Optimization with REFLEX. NEC Tech. J. 2016, 11, 1. [Google Scholar]
  5. Johnson, R.M.; Reiley, D.H.; Muñoz, J.C. “The War for the Fare”: How Driver Compensation Affects Bus System Performance; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2005. [Google Scholar]
  6. Randall, E.R.; Condry, B.J.; Trompet, M.; Campus, S.K. International bus system benchmarking: Performance measurement development, challenges, and lessons learned. In Proceedings of the Transportation Research Board 86th Annual Meeting, Washington, DC, USA, 21–25 January 2007. [Google Scholar]
  7. Welding, P. The instability of a close-interval service. Oper. Res. Soc. 1957, 8, 133–142. [Google Scholar] [CrossRef]
  8. Eberlein, X.J. Real-time control strategies in transit operations: Models and analysis. Transp. Res. Part A 1997, 1, 69–70. [Google Scholar]
  9. Hickman, M.D. An analytic stochastic model for the transit vehicle holding problem. Transp. Sci. 2001, 35, 215–237. [Google Scholar] [CrossRef]
  10. Bartholdi, J.J.; Eisenstein, D.D. A self-coördinating bus route to resist bus bunching. Transp. Res. Part B Methodol. 2012, 46, 481–491. [Google Scholar] [CrossRef]
  11. Delgado, F.; Munoz, J.C.; Giesen, R. How much can holding and/or limiting boarding improve transit performance? Transp. Res. Part B Methodol. 2012, 46, 1202–1217. [Google Scholar] [CrossRef]
  12. O’Flaherty, C.; Mancan, D. Bus passenger waiting times in central areas. Traffic Eng. Control 1900, 11, 419–421. [Google Scholar]
  13. Barnett, A. On controlling randomness in transit operations. Transp. Sci. 1974, 8, 102–116. [Google Scholar] [CrossRef]
  14. Turnquist, M.A. A model for investigating the effects of service frequency and reliability on bus passenger waiting times. Transp. Res. Rec. 1978, 663, 70–73. [Google Scholar]
  15. Gkiotsalitis, K.; Maslekar, N. Improving Bus Service Reliability with Stochastic Optimization. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), Las Palmas, Spain, 15–18 September 2015; pp. 2794–2799. [Google Scholar]
  16. Bates, J.; Polak, J.; Jones, P.; Cook, A. The valuation of reliability for personal travel. Transp. Res. Part E Logist. Transp. Rev. 2001, 37, 191–229. [Google Scholar] [CrossRef]
  17. Daganzo, C.F. A headway-based approach to eliminate bus bunching: Systematic analysis and comparisons. Transp. Res. Part B Methodol. 2009, 43, 913–921. [Google Scholar] [CrossRef]
  18. Friedman, M. A mathematical programming model for optimal scheduling of buses’ departures under deterministic conditions. Transp. Res. 1976, 10, 83–90. [Google Scholar] [CrossRef]
  19. Yan, S.; Chen, H.L. A scheduling model and a solution algorithm for inter-city bus carriers. Transp. Res. Part A Policy Pract. 2002, 36, 805–825. [Google Scholar] [CrossRef]
  20. Niu, H.; Tian, X. An approach to optimize the departure times of transit vehicles with strict capacity constraints. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
  21. Gkiotsalitis, K.; Cats, O. Exact Optimization of Bus Frequency Settings Considering Demand and Trip Time Variations. In Proceedings of the Transportation Research Board 96th Annual Meetings, No: 17-01871, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
  22. Ceder, A.A.; Hassold, S.; Dano, B. Approaching even-load and even-headway transit timetables using different bus sizes. Public Transp. 2013, 5, 193–217. [Google Scholar] [CrossRef]
  23. Sun, D.J.; Xu, Y.; Peng, Z.R. Timetable optimization for single bus line based on hybrid vehicle size model. J. Traffic Transp. Eng. 2015, 2, 179–186. [Google Scholar] [CrossRef]
  24. Chen, Q. Global optimization for bus line timetable setting problem. Discret. Dyn. Nat. Soc. 2014, 2014. [Google Scholar] [CrossRef]
  25. Gkiotsalitis, K.; Stathopoulos, A. Demand-responsive public transportation re-scheduling for adjusting to the joint leisure activity demand. Int. J. Transp. Sci. Technol. 2016, 5, 68–82. [Google Scholar] [CrossRef]
  26. Gkiotsalitis, K.; Stathopoulos, A. Joint leisure travel optimization with user-generated data via perceived utility maximization. Transp. Res. Part C Emerg. Technol. 2016, 68, 532–548. [Google Scholar] [CrossRef]
  27. Shi, R.J.; Mao, B.H.; Ding, Y.; Bai, Y.; Chen, Y. Timetable optimization of rail transit loop line with transfer coordination. Discret. Dyn. Nat. Soc. 2016, 2016. [Google Scholar] [CrossRef]
  28. Cattaruzza, D.; Absi, N.; Feillet, D.; González-Feliu, J. Vehicle routing problems for city logistics. EURO J. Transp. Logist. 2017, 6, 51–79. [Google Scholar] [CrossRef]
  29. Du, T.C.; Li, E.Y.; Chou, D. Dynamic vehicle routing for online B2C delivery. Omega 2005, 33, 33–45. [Google Scholar] [CrossRef]
  30. Dueker, K.J.; Kimpel, T.J.; Strathman, J.G.; Callas, S. Determinants of bus dwell time. J. Public Transp. 2004, 7, 2. [Google Scholar]
  31. TfL Transport for London: Bus Routes and Borough Reports. Available online: https://www.tfl.gov.uk/forms/14144.aspx (accessed on 1 December 2017).
  32. LTA Land Transport Authority: Bus Service Reliability Framework. Available online: http://www.lta.gov.sg/data/apps/news/press/2014/20140124BSRF(final2)-Annex.pdf (accessed on 1 December 2017).
  33. Van Oort, N. Incorporating service reliability in public transport design and performance requirements: International survey results and recommendations. Res. Transp. Econ. 2014, 48, 92–100. [Google Scholar] [CrossRef]
  34. De-rong, T.; Jing, W.; Han-bo, L.; Xing-wei, W. The optimization of bus scheduling based on genetic algorithm. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; pp. 1530–1533. [Google Scholar]
  35. Shrestha, A.; Mahmood, A. Improving Genetic Algorithm with Fine-Tuned Crossover and Scaled Architecture. J. Math. 2016, 2016. [Google Scholar] [CrossRef]
  36. Tsai, C.W.; Tseng, S.P.; Chiang, M.C.; Yang, C.S.; Hong, T.P. A high-performance genetic algorithm: Using traveling salesman problem as a case. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
  37. Dorbritz, R.; Lüthi, M.; Weidmann, U.; Nash, A. Effects of onboard ticket sales on public transport reliability. In Transportation Research Record: Journal of the Transportation Research Board; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2009; pp. 112–119. [Google Scholar]
  38. Hollander, Y.; Liu, R. Estimation of the distribution of travel times by repeated simulation. Transp. Res. Part C Emerg. Technol. 2008, 16, 212–231. [Google Scholar] [CrossRef]
  39. TfL Bus Routes & Borough Reports. Available online: https://tfl.gov.uk/forms/14144.aspx?borough=Barking+ (accessed on 1 December 2017).
  40. Lopez-Garcia, P.; Onieva, E.; Osaba, E.; Masegosa, A.D.; Perallos, A. A hybrid method for short-term traffic congestion forecasting using genetic algorithms and cross entropy. IEEE Trans. Intell. Transp. Syst. 2016, 17, 557–569. [Google Scholar] [CrossRef]
©Text is available under the terms and conditions of the Creative Commons-Attribution ShareAlike (CC BY-SA) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback