Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Demography
Migration is defined as the permanent change in an individual’s usual residence. Forecasting migration is an important requisite for population forecasts or for planning in fields that depend on the future size and structure of the population, such as economics, epidemiology, social insurance, or infrastructure. As migration is the most volatile of all demographic components, its modeling is especially difficult. International migration can be modeled and forecast very differently; users should be familiar with the flaws and strengths of these different approaches.
- demography
- forecasting
- international migration
- gross migration
- net migration
- labor market
1. Introduction
International migration is a global phenomenon with a current estimate of 281 million people globally being counted as migrants, defined as living outside one’s country of origin, with an increasing tendency [1]. Reasons for migration are diverse, and classically defined by Lee [2] into the two categories of push and pull factors, with the first being factors repelling individuals from their region of origin, such as violent conflicts, poor nutritional and health standards, lack of work, or restrictions to freedom of speech. Pull factors instead are those attracting individuals to a specific region, such as better opportunities in employment or education, or better climatic circumstances. Issues arising from international migration differ very much between countries witnessing mostly negative net migration (origin countries) in comparison to those with regular positive net migration (target countries (the notions actually address the origin and the target country associated with one specific migration. We, however, borrow them here to characterize groups of countries)). The first case is low- to middle-income regions, i.e., large parts of Latin America, Africa, Asia, and Eastern Europe. The latter case is high-income regions, i.e., Western Europe, North America, Oceania, or Western Asia [1]. Whereas migration outflows from origin countries are often characterized by the loss of young and qualified individuals (brain drain), which then hampers the development of these countries [3], high inflows to the target countries are sometimes seen as problematic if the migrants originate from less developed and less egalitarian countries, in which case the migrants are perceived as a threat to security or the social systems of the target country by critics [4]. On the backhand side, migration can be seen as a chance. Outflows from origin countries might release tensions on the labor markets there if there is an oversupply of the labor force, which may lead to higher burdens on social systems. In the target countries, inflows by young migrants can be interpreted as a potential stabilizer for the age structure of the population and supply a potential labor force [4]. These societies, in most cases, are affected by a demographic transition, marked by low fertility and decreasing mortality rates, which then leads to aging and depopulation if not averted by immigration [5].
Forecasting is a crucial element of demographic research, with research institutes, political institutions, and enterprises being dedicated to this field since at least the mid-19th century (see, for instance, the historical account in [5]). The three main drivers of national population forecasting are fertility, mortality, and international migration, with the latter being special in the sense that it is the most volatile demographic component [5] and is significantly influenced by sudden events, such as violent conflicts, which are themselves in many cases unpredictable [5][6]. Since population forecasting is an indispensable basis for planning in, for example, economics, infrastructure, health, education, or social insurance [7], sound migration forecasting approaches are of considerable importance. Therefore, users of migration projections (regarding the distinction between forecasts and projections, see, for instance, [7]) should be well aware of their respective assumptions and accompanying limitations. Our contribution aims to present and discuss different approaches for readers who are unfamiliar with the practice of migration forecasting. As an important case study for the further implementation of migration forecasts in economic planning, we show how different migration projection approaches influence population and labor market projections. Our example focuses on Germany as the most populous country of the European Union (EU) [8], which has been an important destination country for migrants since the end of World War II (see Section 3). Our conclusions apply qualitatively to other countries as well, however.
For decades, Germany’s official statistics have shown a positive migration balance (see Section 3)—with only a few exceptions. Germany has been a low-fertility country since the early 1970s, defined as having a total fertility rate below replacement level [9]. This, in turn, is associated with a process of natural negative population growth and aging [5]. The consequences of this process are becoming noticeable in the labor market, because, unlike in the past, the domestic potential labor force is no longer growing [10]. Against this backdrop, institutions such as the German Council of Economic Experts (Sachverständigenrat zur Begutachtung der gesamtwirtschaftlichen Entwicklung—SVR) (see, e.g., ref. [11]) and the Deutsche Bundesbank [12] discuss the risks to the economy and the social security systems associated with skill shortages due to changing demographics. The public debate is currently characterized by hopes of acquiring skilled labor from abroad on the one hand and by fears of security risks caused by high immigration levels on the other hand, especially since the refugee crisis of 2014–2016 [13][14][15].
The questions to be answered in this respect include how much immigration would be necessary from a labor market perspective and what level of immigration Germany can expect in the future. Concerning the first question, the scientific literature does not agree on this point. In particular, opinions differ regarding whether the domestic labor reserves and trends in digitization will be able to compensate for the decrease in the potential labor force associated with changing demographics [16][17][18][19]. Additionally, the development of the demand for labor [19] and the ability of the economy to adapt to changes in the basic conditions via the wage–price mechanism must also be taken into account (e.g., ref. [20][21]). The effect of population aging, in contrast, is consistently seen as leading to a substantial decrease in the population of working age if there is no immigration. This will create diverse problems for the labor market and the social security system [5][22][23][24]. Previous population studies on Germany or the EU in general that examined the target immigration threshold needed to stabilize certain socially relevant indicators (such as the old-age dependency ratio) concluded that an extremely high level of net immigration would be required [25][26]. For example, to maintain the so-called support ratio, the reciprocal of the old-age dependency ratio, at a steady level, the United Nations (UN) calculated that Germany would need average net immigration of 3.4 million persons per year in the period from 1995 to 2050. This could well be difficult for society to deal with, considering the public debate surrounding the immigration of refugees since 2015 [27]. If, on the other hand, the target value is defined as a level of immigration that holds the size of the working population constant, then the annual net immigration according to the UN study would be just under 460,000 migrants. More recent estimates find that net immigration of about 400,000 persons would be required for a constant potential labor force [19]. From a labor market perspective, Brücker et al. [28] see a clear need for a constant or only slowly shrinking potential labor force. This leads to the second question of what immigration level Germany can expect in the future. The present study addresses this important question, as the projections available for Germany differ considerably concerning the expected level of migration. This is, above all, due to issues of methodology, as we will demonstrate.
Next to the overall discussion of previous approaches in migration forecasting, the focus of our paper is to illustrate how different modeling approaches in international migration forecasting impact the outcome of population forecasts and, as an important case study, labor market forecasts building on these population forecasts. We will show with a simple example of Germany how approaches commonly used by most statistical offices can lead to improbable results and flawed implicit assumptions by comparison of migration flow predictions and their resulting assumptions on migration rates. Moreover, we will stress the importance of a stronger focus on emigration modeling and the connection between emigration and immigration, which are both rather underinvestiged in the literature—with the connection between emigration and immigration being typically completely ignored in migration forecasts.
In the next chapter, we therefore first examine selected approaches for projecting migration. Section 3 describes the development of migration in Germany since the 1960s. The historical context serves to explain the problems involved in such projections and the determinants of migration processes. The subsequent Section 4 illustrates the effect of different simulation models on selected indicators of population trends. Finally, we discuss the results of our study in the context of migration policy and conclude with an outlook.
2. Approaches to Migration Modeling and Forecasting—A Brief Overview
Forecasting of migration has been conducted since at least the mid-19th century, with the Census Bureau of England and Wales [29] performing a deterministic 20-year projection of net migration based on population trends observed since the 17th century. Whelpton [30] later predicted international migration and internal migration between rural and urban areas for the United States over a 50-year horizon, discriminated by age, sex, and ethnic group based on migration trends since the beginning of the 20th century. The focus of migration modeling in later years went more to explaining why persons migrate, as formulated in Lee’s [2] earlier mentioned Push–Pull model, being inspired by Ravenstein’s Laws of Migration stated in the late 19th century, first for the United Kingdom (UK) [31], later investigated for other countries with empirical data [32]. In a seminal contribution, Rogers and Castro [33] identified strong and remarkably similar age patterns in intraregional migration for a multitude of countries. The derived model to date is the standard in the age-specific analysis of migration, be it international or internal migration. Since then, the foci of research in migration modeling has been on the improvement of migration data [34], and more sophisticiated migration forecasting, especially the development of probabilistic migration forecast models (see, for instance, [4][35][36])
International migration is the demographic component associated with the greatest uncertainty in the future development of a country’s population [5]. Migration is distinguished by immigration, emigration, and their difference, net migration. This brings us to the first problem a forecaster needs to address: Should immigration or emigration be modeled separately, or should net migration be modeled? This depends on the forecaster’s statistical capabilities and the availability and reliability of the data. First, emigration and immigration exhibit a strong correlation, with emigration being highly influenced by immigration in previous periods (see Section 3 on this for the case of Germany). These correlations are easier to integrate into a net migration model. Second, forecasting net migration instead of gross migration reduces the dimensionality in the forecasting problem. Third, by nature, gross migration cannot take negative values. Trajectories of future migration, however, can indeed take negative values in a simulation. Therefore, gross migration would need to be transformed to ensure that no impossible values would be generated in the forecast. Net migration cancels the need for migration data to be transformed further. Fourth, it may, on some occasions, be inevitable to use net migration if there are no detailed data available on migration but only on migrants (i.e., no flow data but estimated stocks of migrants) [4].
Conversely, there are strong arguments in favor of forecasting gross migration. Motives for migrating from a country differ very strongly from those for migrating to a certain country. For instance, international migration to Germany is primarily for humanitarian, labor-related, or educational reasons [37]. Apart from remigration and, to a lesser extent, emigration for education purposes, emigration from Germany is often associated with better chances of a higher income or more interesting jobs, as well as a general interest in making new experiences abroad. Other reasons for leaving Germany are hopes of a more comfortable life due to a different lifestyle or a milder climate than that in Germany [38]. Therefore, the time series of emigration can vary substantially in terms of their trend and their volatility in comparison to the immigration series. Moreover, emigrants can differ considerably from immigrants regarding their demographics or education [4]. It is easier to model the trends and sensitivity of gross migration than those of net migration, which is a synthetic measure, as there is no such thing as a net migrant [39]. This leads to the second advantage of gross migration over net migration. Modeling gross migration yields a more direct interpretation, as every migrant is one individual, which makes it more intuitive to understand. Third, modeling gross migration is preferable for further analysis based on the migration forecast. If, for example, we model the labor market effects of migration, it is more accurate to address individuals leaving the domestic labor markets than individuals entering it after migrating, as migrants typically need some time to translate their human capital after migration compared to someone who has held a job for years [40].
The stratification of the groups of migrants is another critical point. The tendency to migrate may on average differ quite much between genders and by age group, with high peaks typically in the young labor age and young children’s age [33], for instance. Moreover, the possibility of cross-border migration and the tendency to leave one’s country of origin because of the earlier mentioned push factors varies geographically. Furthermore, some countries attract migrants from certain countries more than others because of historical connections, and associated with this, already existing networks in the target countries or a cultural closeness between origin and target country, e.g., expressed by language. Therefore, modeling migration by demographics, including country of origin or nationality, can cover heterogeneity in migration rates between different groups of migrants. Such an analysis can be more informative and also more detailed and accurate. Vanella and Deschermeier [4], for instance, suggest forecasting by age, sex, and nationality groups within a principal component framework to cover differences and correlations between migration flows of different demographic and geographic groups. However, such an analysis might not be always feasible, as it (ideally) requires long time series of migration data stratified by age, sex, and nationality.
As an alternative to migration flows, many researchers suggest employing migration rates instead (see, e.g., ref. [22][36]). The use of rates instead of flows has philosophical advantages, as our predicted migration flows are adjusted to the population at risk of migration. If the population at risk shows strong trends of structural change over time in terms of size or age structure, the time series of migration flows originating from that specific population are quite sensitive to these population developments. In the first case, the population at risk of migration is smaller. A different age structure of the baseline population will impact migration flows, too, as migration follows strong age patterns, with relatively high migration rates among young adults and an echo effect of elevated migration rates found in the young children accompanying their migrating parents [33], which underlines the importance of considering migration forecasting from a labor perspective. Moreover, forecasting migration flows could lead to negative estimates of population stocks if the sum of deaths and emigration exceeds immigration. This might be the case for older age groups, which are often thinned out [5]. However, forecasting migration rates entails other limitations. In the cases mentioned above, in which we lack data on migration flows, it is not possible to derive subsequent migration rates. Moreover, for some countries with less well-developed statistical reporting systems, detailed population data are unavailable or are flawed [41]. Migration rates computed from the migration flows and the population estimates would then also be highly flawed. Moreover, the computation of immigration rates is either not possible or not feasible, as an immigration rate would have to be computed by dividing the immigration flows by the population at risk in the country or region of origin [4]. In this case, it would also be necessary to decide whether to relate to the population of the country of origin—which would increase the dimensionality massively and could lead to biased results for some variables, as explained—or to the global population, which is quite error-prone due to inaccurate reporting in some global regions [42]. A compromise could be to combine immigration flows with emigration rates in the forecast model.
Another critical point when selecting a model for migration forecasting is the incorporation of uncertainty, with deterministic or stochastic approaches being the main distinction [7]. Most migration (and population) projections are deterministic [43]. They assume some future migration development derived from some mathematical or statistical model that is fed by either theoretical considerations, data, or expert judgment [36]. Uncertainty in the projection is then addressed by varying assumptions regarding the input parameters, which generates further trajectories of the future development [44]. Deterministic approaches are quite easy to construct and understand. However, they suffer from several limitations, including the missing quantification of future developments by probabilities. We do not intend to go into this in more detail; interested readers are referred to a more detailed discussion on this in [7]. Stochastic approaches are preferable, as they not only allow uncertainty to be incorporated into the forecasts but can also cover autocorrelations and cross-correlations in the different migration variables [5] (e.g., the correlation between immigration and emigration or correlations between the immigration of different age groups). For instance, a strong immigration shock for males in the 25–29 age group will be strongly correlated with the immigration figures for females in the same age groups, as partners often migrate as a couple.
Another point of discussion is the basic nature of the forecast model. Most models are time series approaches of some kind. These have the advantage of being quite simple to handle, as their mathematical structure is relatively efficient. Moreover, they permit the coverage of past trends very well and allow for the quantification of uncertainty in the forecast based on historical data [4]. Time series data are not always available with sufficient length and consistency, however. Moreover, even reliable time series data may not always be representative of the future development if, for example, extraordinary events have occurred in the past which will (almost) certainly not be repeated in the future [7]. In the European experience, for instance, there has been a significant change in the opportunities of cross-border migration over time. The European system with free movement over country borders had its origin in the European Economic Community (EEC), which was born in 1957, consisting of West Germany, France, Italy, the Netherlands, Belgium, and Luxembourg. This introduced stronger economic connections among the founding members [45] and was associated with large increases in labor migration, especially to Germany (see Section 3). The EEC was then enlarged by the UK, Ireland, and Denmark in 1973. In 1981, Greece became a new member, followed by Spain and Portugal in 1986. The fall of the Iron Curtain, marked by the reunification of Germany and the split of the Soviet Union and Yugoslavia in the following years, was a landslide event which changed migration between Eastern and Western Europe significantly. In 1993, the EU was ushered, which, among other agreements, aimed at a coordinated migration policy among the member countries (EU-12). In 1995, Austria, Finland, and Sweden entered the EU as new members (EU-15). In 2004, the EU-15 was enlarged by ten (primarily) Eastern European countries (Czechia, Latvia, Lithuania, Hungary, Malta, Poland, Slovakia, and Slovenia), forming the new EU-25. The EU enlargement then reached its peak with the inclusion of Romania and Bulgaria in 2007 and Croatia in 2013 [45].
The described historic developments of the EU borders have been associated with significantly different possibilities in geographic freedom of movement in Europe and therefore had large impacts on international migration patterns. Lately, the UK left the EU (Brexit), which might have implications for future migration, as well, which is not mirrored in the time series data yet available. The EU example illustrates the connection between political decision-making and international migration. Therefore, the connection between migration forecasting and baseline past data on migration trends has always been considered regarding the suitability of time series for a concrete forecast endeavor. An alternative to time series models could be econometric time series models, which explain migration as a result of underlying socioeconomic phenomena [46]. As migration is heavily influenced by socioeconomic or political trends, it could make sense to predict future migration flows based on our current knowledge or ideas of future development in the explanatory factors. This kind of model can be very informative but can, however, be quite difficult to operationalize in a stochastic model, as it would be necessary to cover the uncertainty in the explanatory variables correctly to predict the uncertainty in the migration forecast.
As an alternative to these pure frequentist approaches described, Bayesian models allow stochastic forecasting based on qualitative data (such as expert interviews) [36]. They can also be used to merge quantitative and qualitative information—for example, to adjust perceived limitations in available data with the aid of qualitative knowledge, making Bayesian approaches very flexible. Bayesian forecasts, however, are relatively difficult to conduct, as they are regularly based on a Markov chain Monte Carlo simulation. Moreover, they are quite complex by nature, which makes it hard, and sometimes unfeasible, to integrate uncertainty and correlations between different variables correctly. Moreover, in philosophical terms, it is questionable how trustworthy a Bayesian forecast can be, given that it is (at least partially) based on qualitative, i.e., subjective, information, which might be biased by misinformation or the opinion of the experts involved in the forecast [7]. A longer discourse on potential approaches in Bayesian forecasting of international migration would exceed the scope of this paper. The interested reader is, however, referred to the compilation by Bijak [36]. We see that even scientific projections are based on assumptions and decisions made by forecasters. Migration projections are generally subject to significant future risk, such that even statistical approaches are unable to predict the future development perfectly. The major advantage of the stochastic approach, however, is that, in contrast to deterministic models, all conceivable scenarios can be covered and are quantified with probabilities [4][5][7].
For Germany, a brief review of current stochastic projections reveals a considerable range in the resulting mean net immigration. Deschermeier [6] calculates mean net immigration of 310,000 persons per year for the period from 2016 to 2035. Fuchs et al. [22], on the other hand, estimate net immigration for the years 2015 to 2060 at only 140,000 persons per year on average, whereby this falls rapidly and remains at a level below 130,000 from about 2030 onwards. Vanella and Deschermeier [5] predict mean net immigration of more than 270,000 persons per year until 2045. Azose et al. [35] project the median net migration in Germany to be as high as over half a million persons per year by 2050. Stochastic projection models do not automatically reach the same results, either, but differ concerning the projected distributions of annual migration, in terms of both the mean and its variance. This can be explained partly by the baseline year and partly by the projection horizon. Methodological aspects are likely to play a role, too, as the studies also differ concerning the way they model migration. It is to be assumed further that this also applies for deterministic projections since the methodological differences also exist for deterministic approaches (see the overview in [47] for the UK). There, the discrepancies between the ex-ante model assumptions and the ex post observations are even more crucial, as the initial model assumptions are more restrictive and are not relativized by quantifying the risk as would be the case in stochastic approaches [4].
The extensive literature on migration deals mainly with content-related aspects and less with methodological ones. The focus is, above all, on analyses of factors that affect migration (see, e.g., ref. [48][49][50][51]). Reference is made to economic, institutional, and legal basic conditions, labor market performance (such as wages, unemployment), the presence of fellow countrymen or relatives and friends (in the context of network theory), and numerous other factors. Yet, these factors have rarely been included in projection models to date. One major reason for this is likely to be that the corresponding statistics are only available to a limited extent and are also generally obtained from surveys with relatively low case numbers. This also holds for the studies mentioned above. Moreover, it is difficult to combine the results of these studies with the data contained in the migration or population statistics. A projection model would require detailed time series data covering a long period, which could then be used for projections using structural equation models or Bayesian models (see [36]). What is even more important for projection models is that the factors mentioned would themselves have to be projected. However, the economic development or the labor market situation is likely to be even more difficult to project over a longer time horizon than the demographic trends [4]. Advantageously, the migration cycle is fairly stable over the life course [52], which makes it relatively easy to estimate the age structure of the migrants in the context of a projection study.
Our paper disregards explanatory factors of migration and instead concentrates on the above-mentioned aspects of migration modeling. Using a deterministic simulation model, we analyze the relationship between immigration, emigration, net migration, and the emigration rate. We show how these interact in a classic cohort-component model for forecasting future populations. We examine the sensitivity of emigration rates when certain inflows and outflows are assumed, as is executed, for example, in the population projections conducted by Germany’s Federal Statistical Office (Destatis) [53]. In addition, we compare the effects that a different migration modeling approach has on Germany’s predicted population structure and subsequently on the projected labor force, old-age dependency ratio, and the total dependency ratio.
3. Development of Cross-Border Migration in Germany after World War II
One possible differentiation of the migration flows for Germany is a split by nationality. On the one hand, many people of German nationality migrate to Germany from abroad. The official statistics record almost 213,000 inflows of this type for 2019. On the other hand, every year, a considerable number of Germans move abroad for a longer period (or permanently) and are consequently recorded in the migration statistics as outflows. The number of German citizens leaving the country was at a historically high level in 2019, at over 270,000. As has consistently been the case since 2005, the migration balance of German citizens was, therefore, negative [54]. However, the migration of German nationals is of little significance to the size of the population: just under 0.4% of the population of German nationality left the country in 2019 [54][55]. As a comparison: the emigration rate of the foreign population stood at approximately 8.8%, whereby the emigration rate among EU foreigners was especially high, at 13.3% [56][57]. If “pseudo-immigration rates” are calculated by relating the number of inflows to the population resident in Germany, similarly large differences are found (0.3% and 13.3%, respectively [54][55][56][57]). Finally, the migration activity of Germans underlies different conditions to that of foreigners. Ethnic German resettlers are one example of German immigration [58].
As our study focuses on methodological aspects, we concentrate on the migration of foreigners, as we have seen that their migration rates are much higher than for Germans. Figure 1 illustrates the gross and net migration of foreigners in Germany since 1954.
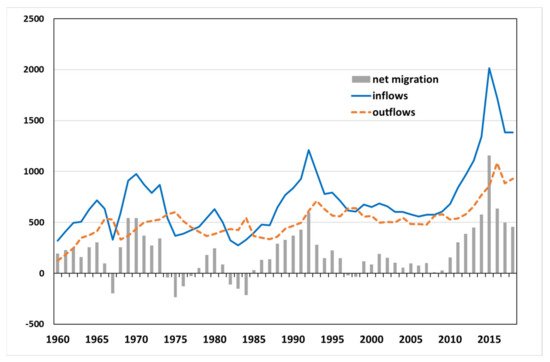
Figure 1. Gross and net migration of non-German migrants (in k), 1954–2018. (Sources: [54]; own design.) Note: Data for the period up until 1990 cover the old territory of the Federal Republic of Germany (including West Berlin); from 1991 onwards, they cover the whole country.
In most of the years covered by the study period, several hundreds of thousands of non-German citizens migrated to Germany from other countries. Between 1954 and 1989, an average of 550,000 foreigners moved to West Germany every year; in the period between reunification and 2018, the number of inflows even averaged 870,000. At the same time, many foreigners left Germany: between 1960 and 1989, an average of 410,000 persons left West Germany per year; since 1990, the figure for unified Germany has been almost 610,000 outflows per year. The peaks and troughs that can be seen in Figure 1 can partly be explained by periods of economic decline, such as the recessions of 1967/68 and 1983, and the subsequent upswings. Some of them are a result of political crises, such as the wars in Yugoslavia in the early 1990s and the refugee crisis in 2015/16 [4][59]. Figure 1 shows very distinctly that immigration peaks are mirrored by increasing emigrations in the subsequent years, i.e., the two series are closely correlated. With a lag of one year between immigration and emigration, the correlation is almost 0.9.
Net migration is reflected in the average migration balance, which stands at just over 200,000 foreigners throughout the entire period since 1960. The migration regimes are likely to have changed in the meantime, however [60]. One reason for this is from the German perspective the enlargement of the EU and the Schengen area, with the free movement of workers constituting a key factor. It has to be taken into account that migration has increased throughout the world, in particular for reasons such as flight and displacement [61], and there is talk of a new migration regime for Germany, too [50]. Indeed, in the period following reunification, i.e., from 1990 to 2018, the average migration balance of the non-German population was considerably higher than earlier values, at 264,000 foreign nationals. This average, however, was influenced by the collapse of the Soviet Union and the wars in Yugoslavia in the early 1990s as well as the conflicts in the Middle East and the Maghreb states in the past decade. Additionally, the economic and financial crisis of 2007/2008 and the eastern enlargement of the EU played a considerable role, in the latter case, especially the free movement of labor for Bulgaria and Romania since 2014 [4][5]. Migration was at lower levels between these periods.
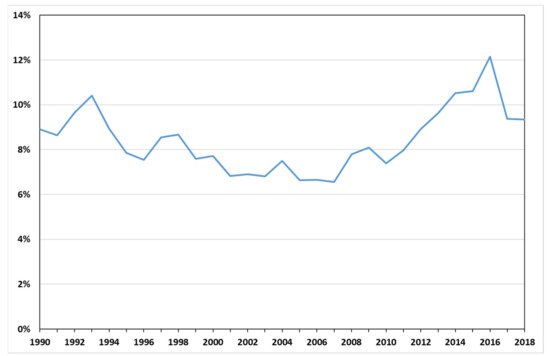
Given the strong correlation between immigration and emigration, it comes as no surprise that there are no considerable fluctuations in the emigration rate with the annual average population, as illustrated in Figure 2. However, a brief but substantial increase in the rate occurred in the wake of the two periods with high levels of forced migration (wars in Yugoslavia, civil wars in the Middle East). The high inflows in these periods were therefore quickly followed by high outflows. The average emigration rate for the period from 1990 to 2018 was 8.4%. One in twelve foreign nationals, therefore, left Germany on average each year.
4. Exemplary Simulations of Migration and the Labor Market in Germany
In the following, we present the data used in our paper and the methodology of our analysis. The basic data were provided by Destatis. A deterministic cohort-component model for population projections developed at the Institute for Employment Research is used as a simulation model. It distinguishes between Germans and foreign nationals, as well as splitting migration into inflows and outflows (for a description of the model, see [62]). This model is used below to calculate several scenarios for the period from 2019 to 2060. The starting year is 2018. To improve the accuracy of the statements, only the migration variables are varied. The assumptions refer solely to the size of the migration flows.
The inflows are based on the age structure of the year 2014, i.e., the conditions prevailing before the strong increase in refugee migration. The age structure of the outflows is also from the year 2014 or is partly an endogenous result of the modeling based on emigration rates. Both age schedules are given in Appendix A. Concerning the breakdown by gender, a 60% male share is assumed for the non-German immigrants, which roughly corresponds to the longer-term average [54]. For the sake of simplicity, the migration balance of German nationals is set to zero. This is not particularly realistic, but the migration of non-Germans is far more relevant for the present research question, as shown earlier. This simplification allows us to concentrate on the key aspect of model comparison.
To compute emigration rates, we need a baseline population, which is computed annually by a cohort-component model, which is the standard in population projections. The cohort-component method updates some population group by adjusting the corresponding population of the previous period by subtracting the deaths in that group in the current period, adding net migration in that group, and adding the children born in the current period [7]:
with
Pt,a,g={Pt−1,a−1,g+Mt,a,g−Dt,a,g for a>0Bt,g+Mt,a,g−Dt,a,g for a=0,
-
Pt−1,a−1,g being the end-of-year population estimate of the previous year in age group a−1 (which is aged a years at the end of the current year) of gender g;
-
Mt,a,g being the net migration during the current year aged a years of gender g, computed as the difference of migration inflows It,a,g and outflows Ot,a,g;
-
Dt,a,g being the deaths in said group;
-
Bt,g being the births of gender g during the current year.
For the overall population, irrespective of demographics, this association becomes:
Pt=Pt−1+Bt+It−Ot−Dt
Concerning the other components of population movement, the model scenarios are based on the following assumptions: the age-specific fertility rates are held constant using a total fertility rate of 1.457 children per German female and 2.1 children per non-German female until 2060. Mortality rates for the whole population are taken from the mortality table of 2015/17 [63], with an increase in life expectancy roughly corresponding to that in the 14th coordinated population projection published by Destatis [53]. As the same assumptions regarding fertility and mortality underlie all the simulations, the effect of the values selected is negligible for these scenarios.
Using these data, we calculate three scenarios with different approaches for modeling migration. The respective model assumptions are shown in Table 1. The first scenario, which is labeled the “level model” below, assumes It=900,000 immigrants and Ot=600,000 emigrants per year. Net migration thus stands at a constant Mt=300,000 persons per year. The age- and gender-specific emigration rates are variable in this model and are the result of the given number of outflows, including their age structure, and the population stock, which, in addition to the natural population movement, is affected by the annual inflows and outflows. The second scenario, termed the “rates model” below, also assumes 900,000 immigrants per year, but holds the age- and gender-specific emigration rates et,a,g at the level recorded in 2012. The year 2012 was chosen because it is before the high levels of immigration (and emigration) that occurred in more recent years. Furthermore, the average emigration rate for the total population in 2012 is almost equal to the long-term average. Gross emigration is the result of the specific emigration rates and the corresponding population stock. Hence, it can be computed as:
Ot,a,g=Pt−1,a,g∗et,a,g.
Table 1. Scenario descriptions.
| Model 1 (Level Model) |
Model 2 (Rates Model) |
Model 3 (Target Model) |
|
|---|---|---|---|
| Inflows | 900,000 | 900,000 | target value (1) |
| Outflows | 600,000 | variable (2) | variable (2) |
| Migration balance | 300,000 | variable (2) | target: 300,000 |
| Emigration rate | variable (2) | constant (3) | constant (3) |
Note: all figures refer to the migration of non-Germans. (1) The number of inflows is set in such a way that a certain migration balance (in this case 300,000) is obtained. (2) The number of outflows and the emigration rates stem from the calculations. (3) Age- and gender-specific emigration rates from the year 2012; the rates are held constant over the entire simulation period.
Net migration is partly endogenous and is therefore variable in this model. The third scenario, designated the “target model” below, assumes the same age- and gender-specific emigration rates as those in the rates model, but models immigration in such a way that there is a migration balance of 300,000 persons each year. In the two scenarios with variable emigration rates, the age- and gender-specific structure of migration occurs endogenously and thus diverges from that in the level model. Due to the logic of the model set, other assumptions are possible only for the level model. Tests using different parameters in the level model resulted in minor differences in the long run, but these did not lead to substantial changes in the results described below.
The simulation results are described below for the period 2019 to 2060. The time horizon is thus long enough to compare our findings with current projections. First, the effects that the modeling approach has on the migration variables are analyzed, subsequently for selected population values. Figure 3 illustrates the simulated emigration rates of the foreign-born population in Germany until 2060 in the three scenarios.
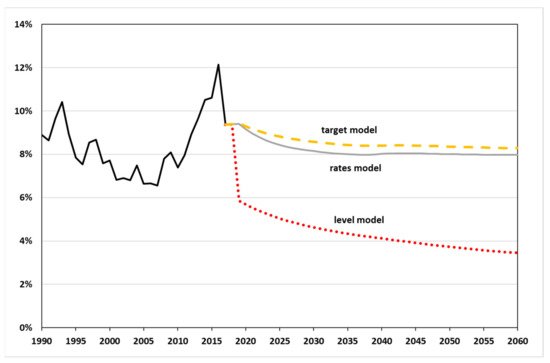
In the level model, the average emigration rate of non-Germans falls dramatically in 2019, the first year of the simulation, and continues to decline afterward. The emigration rate of 3.4%, reached at the end of the simulation period for the non-German population across all age groups and both sexes, is well below the values observed since 1990. In this respect, the level model produces a very improbable development of the emigration rate. In contrast, the simulations with the two models based on fixed emigration rates from 2012 yield an average rate that is similar to the values seen in the past.
Figure 4 shows the simulated total emigration until 2060 based on the three model assumptions. In the level model, emigration is set at 600,000 outflows per year and therefore does not change in the simulation period. This is not the case in the rates model and the target model, however, where the number of outflows depends on the age- and gender-specific rates (and the corresponding population). Although the emigration rates in the rates model and the target model are the same, the number of outflows nonetheless increases substantially in the target model as opposed to the rates model. The reason for this can be seen in the overall context modeled. The outflows are the result of the emigration rates and the population. In the rates model, the annual inflows increase the size of the population ceteris paribus (c.p.) less than for the target model, as a result of which—with constant emigration rates—the number of outflows is higher in the target model than in the rates model.
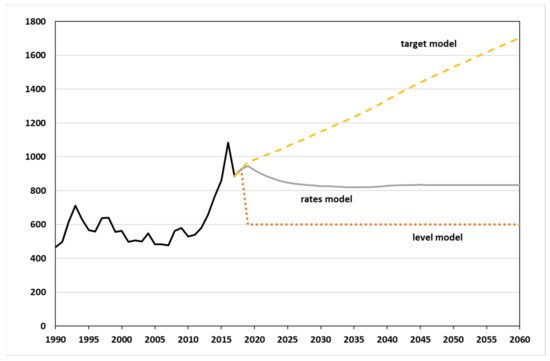
Figure 4. Emigration of the non-German population until 2060 (in k)—simulation results from 2019 onwards. (Sources: [57]; own computation and design.)
Figure 5 illustrates the results of the simulations for immigration. In both the level model and the rates model, the number of inflows remains constant at 900,000 persons during the simulation period, which is in line with the assumptions. In the target model, the amount of immigration required for the envisaged annual net migration of 300,000 persons increases from the current 1.38 million (in 2018) to 2.0 million persons in the year 2060. Under these conditions, an average of 1.63 million foreigners would have to move to Germany every year throughout the entire simulation period from 2019 to 2060; between 1990 and 2018, the corresponding average was about 870,000 inflows.
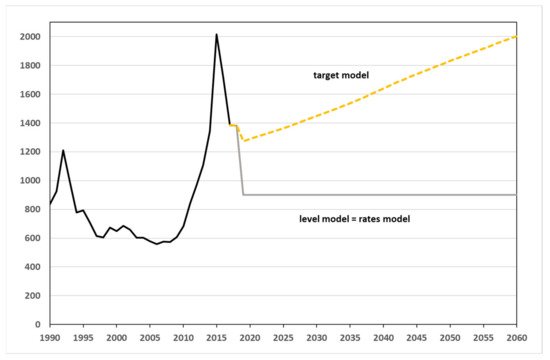
Figure 5. Immigration of the non-German population until 2060 (in k)—simulation results from 2019 onwards. (Sources: [57]; own computation and design.)
Figure 6 portrays the simulated migration balances. In contrast to the level and target models, in which the migration balance was set at 300,000 persons, the rates model estimates the migration balance endogenously. With the given modeling approach, net migration plunges dramatically in the first year of the simulation in the rates model and even becomes slightly negative. Although the migration balance subsequently increases in the rates model, it remains well below its previous values during the remaining simulation period from 2020 to 2060, at about 60,000 net inflows per year (i.e., the long-term average of about 264,000 persons per year from 1990 to 2018).
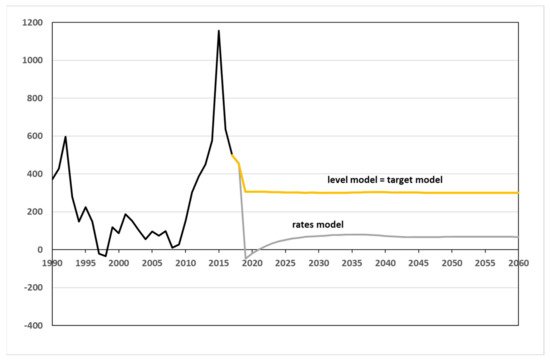
Figure 6. Migration balance of the non-German population until 2060 (in k)—simulation results from 2019 onwards. (Sources: [57]; own computation and design.)
Next, we examine the effect of the different approaches for modeling migration on a population projection. The results for the total population, the working-age population, the old-age dependency ratio, and the total dependency ratio are taken as examples since they are frequently addressed in public debate. In the sense of a sensitivity analysis, the simulations demonstrate how strongly a projection of these statistics reacts to the modeling approach of international migration.
Figure 7 illustrates the simulated development of Germany’s total population until 2060 without differentiating by nationality. The three different model assumptions result in noticeable differences in the predicted population size. In the rates model, the population stock decreases by almost 10.6 million persons (−12.5%) by the end of 2060 compared to the starting population on 31 December 2018. In the case of the level model, on the other hand, the population shrinks only slightly (by 660,000 persons or −0.5%); in the target model, the population increases by almost 3.5 million (+4.5%) by 2060 due to a high level of inflows (especially of younger migrants).
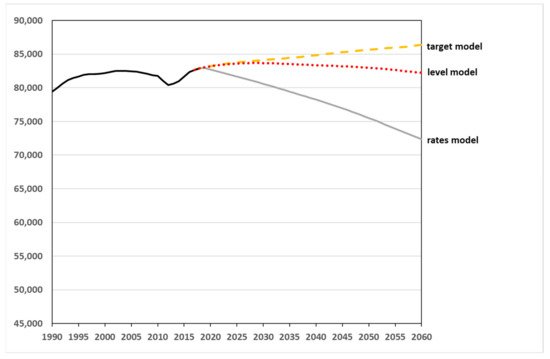
Figure 7. Development of Germany’s population size (Germans and non-Germans) until 2060 (in k)—simulation results from 2019 onwards. (Sources: [55]; own computation and design.)
Figure 8 shows the simulation of the working-age population (defined as being aged between 15 and 64) under the three defined scenarios. We observe decreases in all three cases. However, after 2030, there is a break in the trajectories. This is connected with the baby boomer generation reaching retirement age around 2030, while the relatively young migrants contribute to a rejuvenation of the population. The very high numbers of inflows in the target model even lead to a renewed increase in the size of the working-age population after 2036. As a result, the working-age population decreases by “only” 4.7% by 2060 in the target model, whereas it shrinks by 13% in the level model and by as much as 23.4% in the rates model.
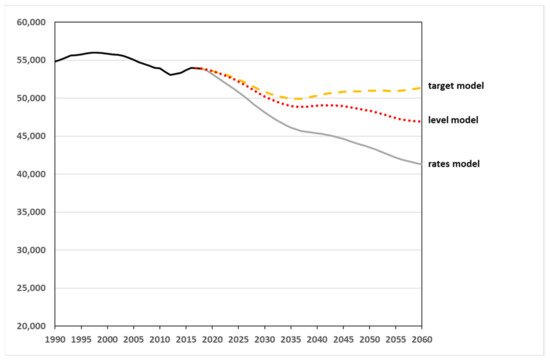
Figure 8. Development of the population aged 15–64 until 2060—simulation results from 2019 onwards. (Sources: [64]; own computation and design.)
Forecasts of the future demographic structure of the population are of similar importance to those of population size in many contexts, such as the labor market [22], pensions [24], long-term care [23], infrastructural planning in health [65], or education [66]. It is also of importance in epidemiology when forecasting the future prevalence of diseases that are more probable in old age, such as cancer [67] or neurodegenerative diseases [68]. The old-age dependency ratio (the ratio of the population over the age of 64 to the working-age population) is a frequently used measure for the stability of the social system, especially pension insurance [22]. In our simulations, the old-age dependency ratio almost doubles by the end of the 2030s in all three scenarios before stabilizing eventually, as can be seen in Figure 9. In the target model, this dependency indicator even decreases slightly from 2038 onwards. In this case, the high immigration and the favorable age structure of the immigrants have a visible impact.
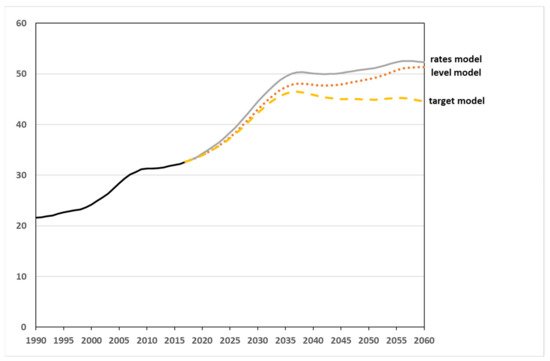
Figure 9. Development of the old-age dependency ratio (as %) until 2060—simulation results from 2019 onwards. (Sources: [64]; own computation and design.)
As a supplement to the old-age dependency ratio, Figure 10 portrays the total dependency ratio, which is an indicator of the burden placed on the working population by the younger and older generations, in other words by people who are mostly not active in the labor market. The total dependency ratio develops similarly to the old-age dependency ratio, i.e., a substantial increase until the end of the 2030s that subsequently levels off clearly. The lines for the three different simulations are closer together than is the case for the old-age dependency ratio. This was to be expected, as the total dependency ratio also includes the population under the age of 15 in the denominator. In the target model, this denominator even grows so strongly as a result of immigration that in the year 2060, the number of people under the age of 15 is 800,000 (+7.3%) higher than the starting value in 2018, at about 11.2 million.
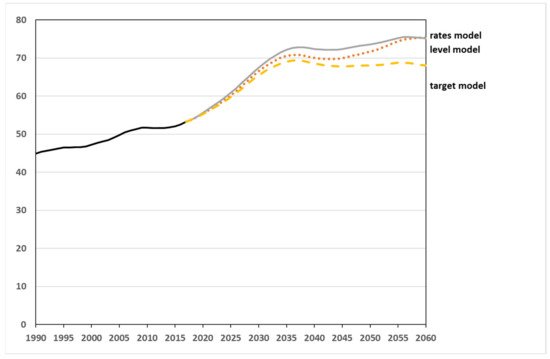
Figure 10. Development of the total dependency ratio (as %) until 2060—simulation results from 2019 onwards. (Sources: [54]; own computation and design.)
The graphs indicate that the models yield less pronounced differences for the dependency ratios in the simulations than is the case for the population stocks. This can be explained by the fact that the different developments of the stocks partly cancel each other out in the dependency ratios.
5. Conclusions and Outlook
We have provided an overview of approaches in migration forecasting, with a special emphasis on approaches conducted by the statistical offices. Therefore, readers who are not familiar with the practice of migration forecasting should gain a good first introduction on this and also understand the strong connections between migration, population, and labor market forecasts. This should make the users of projections in these fields more aware of the limitations associated with their input data. Germany, as the most populous country of the EU and an important target country for migrants, served as a convenient case study. The conclusions derived from our studies, however, hold internationally, as well. As we use a typical cohort-component model and the population data should be available for most countries, our model calculation can easily be reproduced for other countries. The simulations in this paper showed the extent to which migration predictions and therefore also population projections depend on the modeling approach selected. In doing so, no statement is made as to which approach is the “right” one. However, our simulations provide an impetus for discussing the choice of model approach more critically. Popular estimations regarding the level of migration to be expected in the future are based on approaches that are comparable in terms of methodology to the level model (e.g., ref. [53]). Yet, the considerable drop in the average emigration rate that our simulations showed for the level model is probably very unlikely. In this respect, the results of a level model should be subjected to critical scrutiny. In the rates model, with constant emigration rates, on the other hand, the level of net immigration plunged dramatically, even becoming negative at the beginning of the simulation period. Against the backdrop of the migration that occurred in the more recent past, this result initially seems somewhat implausible. However, the feedback mechanism between emigration and immigration that occurs via the rates with the population plays an important role in net migration, as the higher the immigration level is, the higher emigration is, c.p. In this respect, very low or even negative migration balances are quite conceivable, at least in the short term. As mentioned above, stochastic approaches can compensate to some extent for the shortcomings in such deterministic approaches, but these were not the focus of our paper. (See, for instance, [25][30][37] for more detailed discussions of probabilistic models of migration forecasting.)
A limitation in the explanatory value of our simulations is associated with the age- and gender-specific outflow rates, which were held constant. Conceivable improvements could entail differentiating the emigrations, for example, by taking residency permits into account or differentiating by region of origin. We already discussed earlier that migration rates vary strongly between different demographic groups. This does not only cover differences by age and sex, but also strong differences in c.p. migration rates between different nationality groups. Migrants from different countries of origin vary not only in their tendency to migrate and their target countries but also regarding their time to integrate into the labor market and if they will be successfully integrated into the labor market at all. For the example of Germany, labor force participation rates for first-generation female migrants from Turkey or the Maghreb states are much lower than those for females from Southern Europe, which is not the case for males [69]. Ideally, such distinctions should also be covered in a labor market forecast based on migration forecasts. For this, however, the migration and population statistics would have to be linked with the data of the Central Register of Foreigners. Furthermore, it would also be necessary to structure the immigrations in the same way for projections. These are both exceptionally difficult tasks for which we are seeking solutions.
We derive some recommendations from our simulations, both for migration policy and migration forecasting. First, population projections should take account of the relationship between emigration and immigration more explicitly, at least showing the emigration rate in addition. Second, this relationship should also be taken into consideration more strongly in migration policy. The question also arises as to whether or under what conditions a high level of net immigration is realistic in the longer term, as this necessitates a constantly increasing number of immigrations. We, therefore, recommend measures that reduce the emigration rate. One key approach would involve measures aimed at improving the labor market integration of foreigners living in Germany (see [70]). Overall, most projections are yet conducted based on rather naïve deterministic approaches based on gross or net migration flows, which do not cover the high uncertainty associated with future migration, and, as we have seen in the German case study, do not lead to realistic predictions in accompanying population and labor market projections. Next to these limitations, enhancing migration forecasts by more detailed socio-demographic criteria, such as nationality or education, could provide better input for emigration forecasts, as we can assume different probabilities of remigration for different groups of immigrants, and labor market forecasts, as successful labor market integration depends on these factors, as we have seen. Labor market forecasts can be conducted based on labor force participation rates [22], which differ very much by demographics, especially for migrants. We have seen that the academic literature in the past few years has given new impulses on how to improve migration forecasting, which, however, are not yet implemented in most official forecasts. We have also seen why more detailed data on migrants could be of great help for not only to gain a better understanding of the labor market impact of international migration, but also to derive more sophisticated and more accurate labor market forecasts based on these results.
References
- UN. International Migration 2020: Highlights (ST/ESA/SER.A/452); United Nations Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2020.
- Lee, E.S. A Theory of Migration. Demography 1966, 3, 47–57.
- Körner, H. The “Brain Drain” from Developing Countries—An Enduring Problem. Interecon. Rev. Eur. Econ. Policy 1998, 33, 26–29.
- Vanella, P.; Deschermeier, P. A stochastic Forecasting Model of international Migration in Germany. In Familie-Bildung-Migration. Familienforschung im Spannungsfeld zwischen Wissenschaft, Politik und Praxis. Tagungsband zum 5. Europäischen Fachkongress Familienforschung; Kapella, O., Schneider, N.F., Rost, H., Eds.; Verlag Barbara Budrich: Opladen, Germany; Berlin, Germany; Toronto, ON, Canada, 2018; pp. 261–280.
- Vanella, P.; Deschermeier, P. A Probabilistic Cohort-Component Model for Population Forecasting—The Case of Germany. J. Popul. Ageing 2020, 13, 513–545.
- Deschermeier, P. Einfluss der Zuwanderung auf die demografische Entwicklung in Deutschland. IW-Trends. Vierteljahresschr. Zur Empir. Wirtsch. 2016, 43, 21–38.
- Vanella, P.; Deschermeier, P.; Wilke, C.B. An Overview of Population Projections—Methodological Concepts, International Data Availability, and Use Cases. Forecasting 2020, 2, 346–363.
- Eurostat Database. Population on 1 January. Available online: https://ec.europa.eu/eurostat/web/main/data/database (accessed on 28 May 2021).
- Vanella, P.; Deschermeier, P. A Principal Component Simulation of Age-Specific Fertility—Impacts of Family and Social Policy on Reproductive Behavior in Germany. Popul. Rev. 2019, 58, 78–109.
- Bauer, A.; Fuchs, J.; Hummel, M.; Hutter, C.; Klinger, S.; Wanger, S.; Weber, E.; Zika, G. IAB-Prognose 2019/2020: Konjunktureller Gegenwind für den Arbeitsmarkt. IAB-Kurzber. 2019. 18/2019. Available online: http://doku.iab.de/kurzber/2019/kb1819.pdf (accessed on 2 June 2021).
- SVR. Vor Wichtigen Wirtschaftspolitischen Weichenstellungen; SVR: Wiesbaden, Germany, 2018; Volume 18/19.
- Deutsche Bundesbank. Long-term outlook for the statutory pension insurance scheme. In Monthly Report October 2019; Bundesbank, D., Ed.; Deutsche Bundesbank: Frankfurt (Main), Germany, 2019; pp. 53–81.
- Reimann, A. Terrorverdächtige Unter Flüchtlingen. Ein Risiko, Keine Lösung. Available online: https://www.spiegel.de/politik/deutschland/terrorverdaechtige-unter-fluechtlingen-wie-gross-ist-das-risiko-a-1115967.html (accessed on 25 May 2021).
- Schmieder, J. Lohn—und Beschäftigungseffekte der Zuwanderung nach Deutschland. DIW Roundup: Polit. Im Fokus 2016, 90. Available online: https://www.diw.de/documents/publikationen/73/diw_01.c.524303.de/diw_roundup_90_de.pdf (accessed on 2 June 2021).
- Walburg, C. Migration Und Kriminalität—Erfahrungen Und Neuere Entwicklungen. Available online: https://www.bpb.de/politik/innenpolitik/innere-sicherheit/301624/migration-und-kriminalitaet (accessed on 25 May 2021).
- Brenke, K. Fachkräftemangel kurzfristig noch nicht in Sicht. DIW-Wochenber 2010, 46. Available online: https://www.diw.de/documents/publikationen/73/diw_01.c.363686.de/10-46-1.pdf (accessed on 2 June 2021).
- Fuchs, J.; Weber, B. Höhere Erwerbsquoten stoppen nicht den Rückgang des Erwerbspersonenpotenzials. Soz. Fortschr. 2020, 69, 45–71.
- Klüsener, S.; Loichinger, E.; Schneider, N.F.; Sulak, H. Alterung und Arbeitsmarkt: Auswirkungen Weniger Dramatisch Als Vielfach Befürchtet. Available online: https://www.bib.bund.de/Publikation/2019/pdf/Policy-Brief-Alterung-und-Arbeitsmarkt.pdf?__blob=publicationFile&v=6 (accessed on 25 May 2021).
- Fuchs, J.; Kubis, A.; Lutz, S. Zuwanderung und Digitalisierung: Wie Viel Migration Aus Drittstaaten Benötigt Der Deutsche Arbeitsmarkt künftig? Bertelsmann Stiftung: Gütersloh, Germany, 2019.
- Brücker, H.; Christoph, B.; Dietz, M.; Fuchs, J.; Fuchs, S.; Haas, A.; Hummel, M.; Jahn, D.; Kleinert, C.; Kruppe, T.; et al. Fachkräftebedarf: Analyse und Handlungsstrategien. In IAB-Bibliothek 334: Handbuch Arbeitsmarkt 2013. Analysen, Daten, Fakten; Brücker, H.K.S., Möller, J., Walwei, U., Eds.; Bertelsmann Stiftung: Bielefeld, Germany, 2012; pp. 206–290.
- Maier, T.; Neuber-Pohl, C.; Mönnig, A.; Zika, G.; Kalinowski, M. Modelling reallocation processes in long-term labour market projections. J. Labour Mark. Res. 2017, 50, 67–90.
- Fuchs, J.; Sohnlein, D.; Weber, B.; Weber, E. Stochastic Forecasting of Labor Supply and Population: An Integrated Model. Popul. Res. Policy Rev. 2018, 37, 33–58.
- Vanella, P.; Heß, M.; Wilke, C.B. A probabilistic projection of beneficiaries of long-term care insurance in Germany by severity of disability. Qual. Quant. Int. J. Methodol. 2020, 54, 943–974.
- Vanella, P.; Rodriguez Gonzalez, M.A.; Wilke, C.B. The Impact of Population Aging on the German Statutory Pension Insurance. In Stochastic Forecasting in Demography and Social Insurance; Vanella, P., Ed.; Gottfried Wilhelm Leibniz Universität: Hannover, Germany, 2020; pp. 159–197.
- Bijak, J.; Kupiszewska, D.; Kupiszewski, M. Replacement Migration Revisited: Simulations of the Effects of Selected Population and Labor Market Strategies for the Aging Europe, 2002–2052. Popul. Res. Policy Rev. 2008, 27, 321–342.
- UN. Replacement Migration: Is It a Solution to Declining and Ageing Populations? Popilation Division, Ed.; UN Population Division: New York, NY, USA, 2000.
- Siedhoff, M. Replacement Migration: Ein Konzept mit begrenzter Reichweite. Inf. Zur. Raumentwickl. 2018, 2018, 84–95.
- Brücker, H.; Jaschke, P.; Keita, S.; Konle-Seidl, R. Fachkräfteeinwanderung aus Drittstaaten: Zum Referentenentwurf des Bundesministeriums des Innern, für Bau und Heimat. IAB-Stell. 2019. 4/2019. Available online: https://www.econstor.eu/bitstream/10419/207544/1/166810380X.pdf (accessed on 2 June 2021).
- Census Bureau of England and Wales. General Report; with Appendix of Tables 1863. Available online: https://www.visionofbritain.org.uk/census/EW1861GEN/ (accessed on 2 June 2021).
- Whelpton, P.K. Population of the United States, 1925 to 1975. Am. J. Sociol. 1928, 34, 253–270.
- Ravenstein, E.G. The Laws of Migration. J. Stat. Soc. Lond. 1885, 48, 167–235.
- Ravenstein, E.G. The Laws of Migration: Second Paper. J. R. Stat. Soc. 1889, 52, 241–305.
- Rogers, A.; Castro, L.J. RR-81–30: Model Migration Schedules; International Institute for Applied Systems Analysis: Laxenburg, Austria, 1981.
- Willekens, F. Monitoring international migration flows in Europe. Towards a statistical data base combining data from different sources. Eur. J. Popul. 1994, 10, 1–42.
- Azose, J.J.; Sevcikova, H.; Raftery, A.E. Probabilistic population projections with migration uncertainty. Proc. Natl. Acad. Sci. USA 2016, 113, 6460–6465.
- Bijak, J. Forecasting International Migration in Europe: A Bayesian View; Springer Science+Business Media: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2011; Volume 24.
- Bundesamt für Migration. Migrationsbericht der Bundesregierung 2019; Bundesministerium des Innern, für Bau und Heimat (BMI): Berlin, Germany, 2020.
- Engler, M.; Erlinghausen, M.; Ette, A.; Sauer, L.; Scheller, F.; Schneider, J.; Schultz, C. Studie Des SVR-Forschungsbereichs 2015-1; Sachverständigenrat deutscher Stiftungen für Integration und Migration (SVR), Bundesinstitut für Bevölkerungsforschung (BiB), Universität Duisburg-Essen, Eds.; Destatis: Wiesbaden, Germany, 2015.
- Rogers, A. Requiem for the Net Migrant. Geogr. Anal. 1990, 22, 283–300.
- Basilio, L.; Bauer, T.K.; Kramer, A. Transferability of Human Capital and Immigrant Assimilation: An Analysis for Germany. LABOUR: Rev. Labour Econ. Ind. Relat. 2017, 31, 245–264.
- IOM. Global Migration Indicators 2018; International Organization for Migration Berlin: Berlin, Germany, 2018.
- Pelletier, F. Census Counts, Undercounts and Population Estimates: The Importance of Data Quality Evaluation. Available online: https://www.un.org/development/desa/pd/sites/www.un.org.development.desa.pd/files/files/documents/2020/Oct/undesa_pd_tp_2020_tp_population_estimates.pdf (accessed on 31 May 2021).
- Sohst, R.; Tjaden, J.; de Valk, H.; Melde, S. The Future of Migration to Europe: A Systematic Review of the Literature on Migration Scenarios and Forecasts; International Organization for Migration: Geneva, Germany, 2020.
- UN. World Population Prospects 2019: Methodology of the United Nations Population Estimates and Projections; ST/ESA/SER.A/425; United Nations: New York, NY, USA, 2019.
- EU. The history of the European Union. Available online: https://europa.eu/european-union/about-eu/history_en (accessed on 1 July 2021).
- Kubis, A.; Schneider, L. Schätzung der Wanderungsströme von EU-Bürgerinnen nach und aus Deutschland bis 2040. In IAB-Bibliothek 372: Zur Relevanz von Bevölkerungsvorausberechnungen für Arbeitsmarkt-, Bildungs- und Regionalpolitik; Deschermeier, P., Fuchs, J., Iwanow, I., Wilke, C.B., Eds.; wbv Media: Bielefeld, Germany, 2020; Volume 372, pp. 69–92.
- Bijak, J. Migration Assumptions in the UK National Population Projections: Methodology Review; University of Southampton: Southampton, UK, 2012.
- Burkhauser, R.V.; Hahn, M.H.; Hall, M.; Watson, N. Australia Farewell: Predictors of Emigration in the 2000s. Popul. Res. Policy Rev. 2016, 35, 197–215.
- Constant, A.F.; Zimmermann, K.F. Circular and Repear Migration: Counts of Exits and Years Away from the Host Country. Popul. Res. Policy Rev. 2011, 30, 495–515.
- Ette, A.; Heß, B.; Sauer, L. Tackling Germany’s Demographic Skills Shortage: Permanent Settlement Intentions of the Recent Wave of Labour Migrants from Non-European Countries. J. Int. Migr. Integr. 2016, 17, 429–448.
- Kuhlenkasper, T.; Steinhardt, M.F. Who leaves and when? Selective outmigration of immigrants from Germany. Economic Systems 2017, 41, 610–621.
- Rogers, A.; Little, J.; Raymer, J. The Indirect Estimation of Migration: Methods for Dealing with Irregular, Inadequate, and Missing Data; Springer Science + Business Media: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2010.
- Destatis. Bevölkerung im Wandel: Annahmen und Ergebnisse Der 14. Koordinierten Bevölkerungsvorausberechnung; Destatis: Wiesbaden, Germany, 2019.
- Destatis. Wanderungen Zwischen Deutschland und dem Ausland: Deutschland, Jahre, Nationalität, Geschlecht. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 2 June 2021).
- Destatis. Bevölkerung Deutschland, Stichtag, Nationalität. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 2 June 2021).
- Destatis. Ausländer: Deutschland, Stichtag, Geschlecht, Ländergruppierungen. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 2 June 2021).
- Destatis. Wanderungen zwischen Deutschland und dem Ausland: Deutschland, Jahre, Staatsangehörigkeit. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 2 June 2021).
- Ette, A.; Sauer, L. Auswanderung Aus Deutschland: Daten und Analysen Zur Internationalen Migration Deutscher Staatsbürger; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010.
- Bade, K.J.; Oltmer, J. Normalfall Migration; Bundeszentrale für politische Bildung: Bonn, Germeny, 2004.
- Brücker, H. Neue Trends in der Zuwanderung nach Deutschland. In IAB-Bibliothek 363: Arbeitsmarkt kompakt. Analysen, Daten, Fakten; Möller, J., Walwei, U., Eds.; wbv Media: Bielefeld, Germany, 2017.
- OECD. International Migration Outlook 2019; OECD Publishing: Paris, France, 2019.
- Fuchs, J.; Söhnlein, D. Vorausschätzung der Erwerbsbevölkerung bis 2050. IAB-Forsch. 2005, 16/2005. Available online: http://doku.iab.de/forschungsbericht/2005/fb1605.pdf (accessed on 2 June 2021).
- Destatis. Sterbetafel (Periodensterbetafel): Deutschland, Jahre, Geschlecht, Vollendetes Alter. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 8 June 2021).
- Destatis. Bevölkerung Deutschland, Stichtag, Altersjahre. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 5 June 2021).
- Ehrhard, T. Personalbedarfsprognose im Gesundheits- und Pflegewesen: Eine Berufs-, Einrichtungs- und Regionalspezifische Betrachtung für Deutschland; Peter Lang Internationaler Verlag der Wissenschaften: Frankfurt, Germany, 2014.
- Bomsdorf, E.; Babel, B.; Schmidt, R. Zur Entwicklung der Bevölkerung, der Anzahl der Schüler, der Studienanfänger und der Pflegebedürftigen: Stochastische Modellrechnungen für Deutschland bis 2050. Soz. Fortschr. 2008, 57, 125–132.
- Stock, C.; Mons, U.; Brenner, H. Projection of cancer incidence rates and case numbers until 2030: A probabilistic approach applied to German cancer registry data (1999–2013). Cancer Epidemiol. 2018, 57, 110–119.
- Ziegler, U.; Doblhammer, G. Projections of the number of people with dementia in Germany 2002 through 2047. In Ageing, Care Need and Quality of Life; Doblhammer, G., Scholz, R., Eds.; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010; pp. 94–111.
- Algan, Y.; Dustmann, C.; Glitz, A.; Manning, A. The Economic Situation of First and Second-Generation Immigrants in France, Germany and the United Kingdom. Econ. J. 2010, 120, F4–F30.
- Bergseng, B.; Degler, E.; Lüthi, S. Unlocking the Potential of Migrants in Germany. OECD Reviews of Vocational Education and Training; OECD Publishing: Paris, France, 2019.
This entry is offline, you can click here to edit this entry!