1. Introduction

LST plays a key role in the energy balance of the Earth–atmosphere system as well as in ecosystems ^[1][2][3][4]. LST is widely used in various fields, including urban heat islands, drought disasters, and public health ^{[5][6][7][8][9]}, and is also an important input variable in Earth system models, such as meteorological, ecological, hydrological, and biological models ^{[10][11][12][13]}. Large-scale environmental dynamic monitoring necessitates LST datasets with high spatial resolutions and temporal frequencies ^[14]. Field measurements can provide only a limited number of point-scale LST observations and cannot effectively characterize the spatial details of thermal environments. Remote sensing provides an effective way to observe LST and has become the main method to acquire continuous LST datasets over large scales. A series of algorithms have been developed to retrieve LST from TIR remotely sensed data, including the single-channel algorithm ^[15], single-window algorithm ^[16], Wan–Dozier split-window algorithm ^[17], Jiménez–Muñoz split-window algorithm ^[18], and Rozenstein split-window algorithm ^[19]. Based on different satellite data and retrieval algorithms, several LST products have been released, such as MODIS LST ^[20], ASTER LST ^[21], and CGLS LST ^[22]. Among them, the MODIS LST product has been widely used for its advantages of free access, wide coverage, and high accuracy.

However, TIR sensors can only observe land surfaces under cloudless conditions. For cloud-covered areas, TIR sensors can only obtain the cloud-top thermal radiation, and the retrieved temperature does not represent the LST but instead denote the cloud top temperature. The data gaps caused by cloud cover obviously limit the application of remotely sensed LST datasets. It is necessary to fill these data gaps to reconstruct cloud-free LST datasets.

2. Bibliometric Analysis of the Published Literature on LST Reconstruction under Cloudy Conditions

The published papers on LST reconstruction from January 2000 to June 2021 were derived from the Web of Science Core Collection database. The papers containing “reconstruction”, “gap-fill”, and “all-weather” as keywords and “land surface temperature” in the title were retrieved. After manually removing irrelevant papers by checking their abstracts, a total of 70 papers were selected for bibliometric analysis. The Bibliometrix ^[23] package in R was used for the bibliometric analysis.

2.1. Variations in the Number of Published Papers

The search results showed that no relevant papers were published before 2010. Figure 1 shows the variations in the number of publications from 2010 to 2020 (the papers of 2021 are not included because of only covering half of a year). The number of publications grew gradually from 2010 to 2016 and grew rapidly after 2016, with a peak of 14 papers published in 2019. Figure 2 shows the variations of annual citations from 2010 to 2020. The increasing number of citations over the years indicates that LST reconstruction has attracted more attention from researchers. The increasing trends of annual publications and citations suggest that reconstructing remotely sensed LST under cloudy conditions has become a hot research topic in recent years.

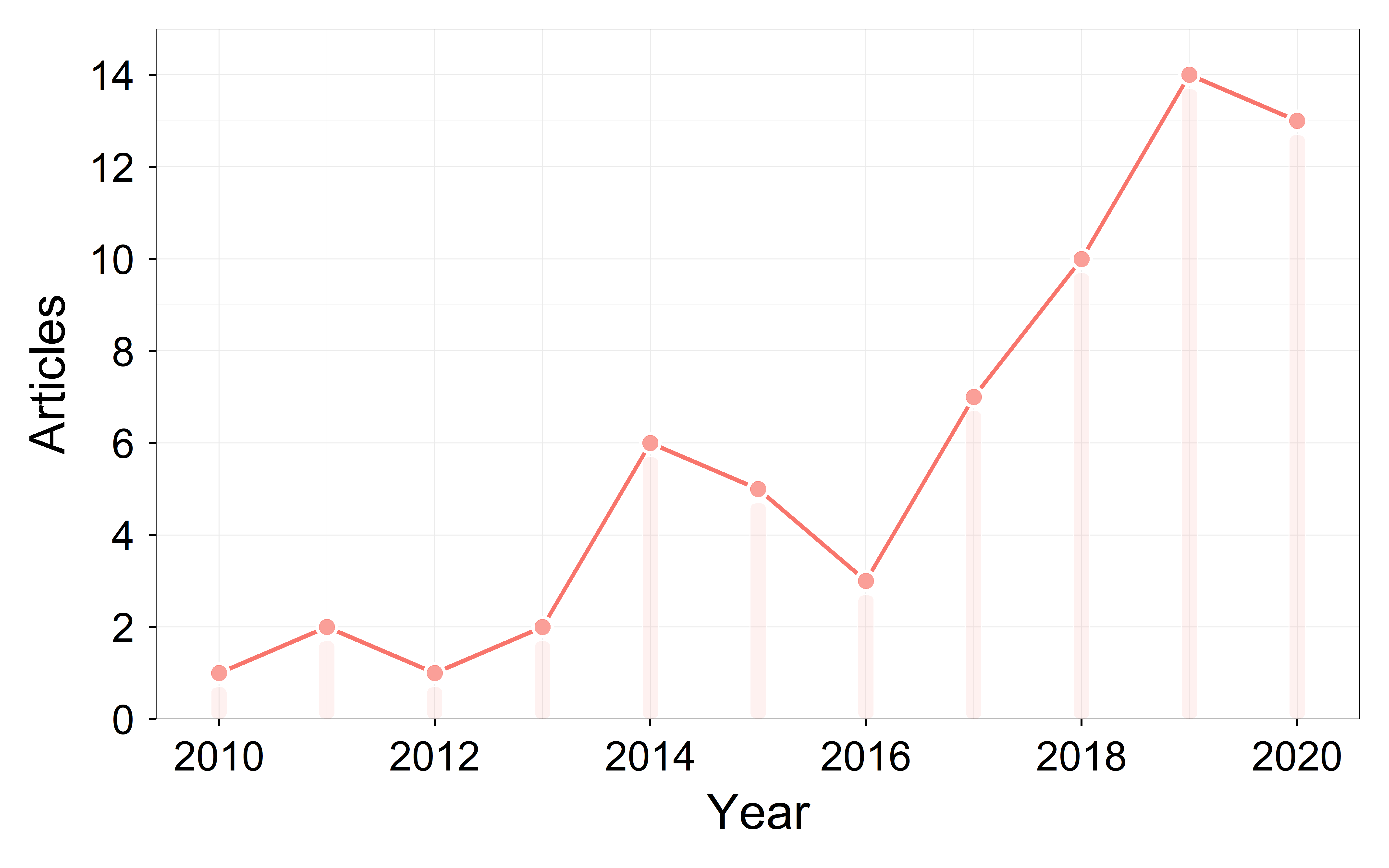
Figure 1. The variations in the number of publications from 2010 to 2020.

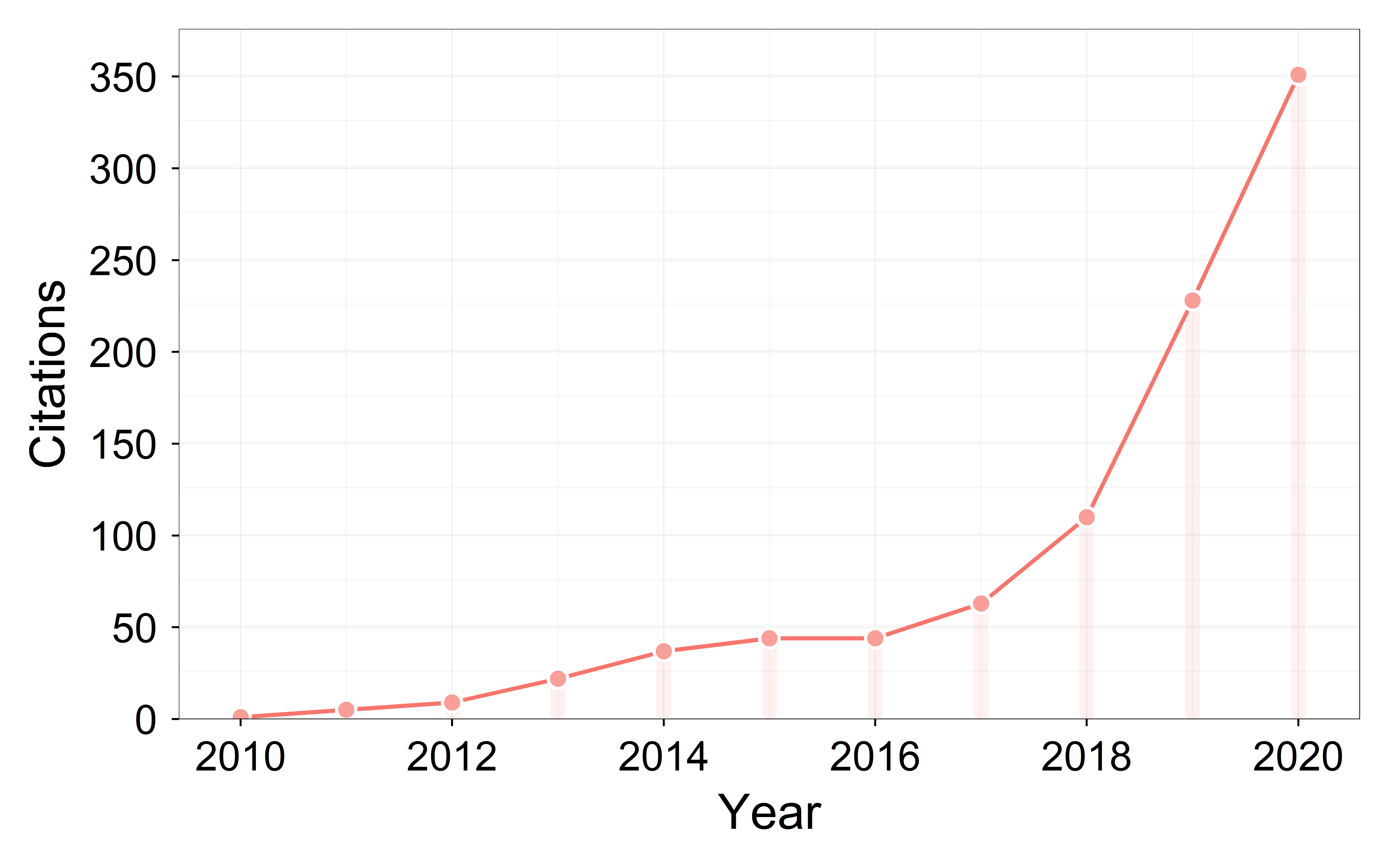
Figure 2. The variations in the number of citations from 2010 to 2020.

2.2. Most Relevant Journals

The 70 papers obtained were published in 26 journals, most of which were in the field of remote sensing. Table 1 lists the top 10 journals with the highest numbers of publications. The publications show significant concentrations in various journals, with the top 3 journals (Remote Sensing, Remote Sensing of Environment, and IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing) accounting for 48.44% of the total number of publications. Remote Sensing ranked first with 16 articles, followed by Remote Sensing of Environment (9) and IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing (6).

Table 1. Top 10 journals with the highest number of publications.

2.3. Most-Cited Papers

The total citations and annual average citations of the 70 papers were counted. Table 2 lists the 10 most cited papers and their citations. The most-cited article was by Neteler [24] and was published in Remote Sensing; this article was cited 172 times in total. The second most-cited article was by Duan [25] and was published in Remote Sensing of Environment, with 96 total citations and the highest annual number of citations, with 19.2.

Table 2. Top 10 papers with the highest number of citations.

2.4. Most-Contributed Countries

The country distribution of the first author’s affiliation of the 70 papers was analyzed. China, USA, Spain, Portugal, France, Turkey, Iran, and Romania has published more than one paper in this field (Table 3), with 63 papers in total. The remaining 7 papers came from 7 different countries. China published far more papers (36) than the other countries, followed by the United States (12). The rest of the countries that published more than one paper were European countries. In terms of the average citations per paper, the United States maintains a leading edge in this research topic, with 23.33 citations per paper, followed by China, with 14.36 citations per paper.

Table 3. Countries with more than one publication.

3. Temperature Datasets Used for LST Reconstruction

Temperature datasets from different sources were used in the reconstruction of remotely sensed LST under cloudy conditions, which include polar-orbiting satellite thermal infrared data, geostationary satellite thermal infrared data, space-borne microwave data, and reanalysis data.

3.1. LST from Polar-Orbiting Satellite Thermal Infrared Data

LST derived from polar-orbiting satellite thermal infrared data is the most common data for LST reconstruction, which has high spatial resolution and moderate temporal resolution. The available datasets include Terra/Aqua MODIS LST, NOAA AVHRR LST, NPP VIIRS LST, and FY-3 VIRR LST. Most of these data have a spatial resolution of 1 km and a temporal resolution of 1 day. To reduce cloud obscuration, multi-temporal LST is composited over 8-day, 16-day, or 1-month periods. The 8-day MODIS LST is widely used for reconstruction.

3.2. LST from Geostationary Satellite Thermal Infrared Data

LST derived from geostationary Satellite Thermal Infrared Data has relatively coarse spatial resolutions but high temporal resolutions. The available datasets include MSG SEVIRI LST, GOES ABI LST, Himawari-8 AHI LST, and FY-4A AGRI LST. The spatial resolutions of these data range from 2 km (Himawari-8 AHI and GOES ABI) to 4 km (FY-4A AGRI), and the temporal resolutions range from 10 min (GOES ABI LST and Himawari-8 AHI) to 15 min (MSG SEVIRI and FY-4A AGRI).

3.3. Subsurface Temperature from Space-Borne Microwave Data

Thermal infrared data have the advantage of high spatial resolution, but can not provide observations under cloud cover. Microwave signals are minimally influenced by atmospheric conditions ^[34], making it possible to retrieve subsurface temperature under cloudy skies. However, it should be noted that surface temperature retrieved from microwave data represents subsurface temperature whereas LST retrieved from thermal infrared data represents surface skin temperature. In addition, space-borne microwave data have some limitations, including coarse spatial resolutions and swath gaps that bring missing values. The popular products include Aqua AMSR-E with a spatial resolution of 25 km and GCOM-W1 AMSR-2 with a spatial resolution of 10 km. Both of them have a temporal resolution of 1 day.

3.4. Temperature from Reanalysis Data

Reanalysis data are produced by assimilating multi-source observations from ground stations, satellites, planes, and ships. These datasets provide air temperature, soil temperature, or skin temperature, which are characterized by high temporal resolutions but coarse spatial resolutions. The popular products include NCEP/NCAR, ERA5, and GLDAS. The spatial resolutions of these data range from 0.25° (ERA5 and GLDAS) to 2.5° (NCEP/NCAR), and the temporal resolutions range from 1 h (ERA5) to 6 h (NCEP/NCAR).

4. Methods of LST Reconstruction

4.1. Spatial Gap-Filling Methods

In spatial gap-filling methods, missing LST values in cloudy regions are spatially interpolated using spatially neighboring valid LST values. Table 4 provides a summary of spatial reconstruction methods and their validation performances.

LST is characterized by continuous spatial distributions and spatial correlations, so spatial interpolation methods can be used to fill LST data gaps under cloudy conditions. Multiple interpolation methods, such as spline curve interpolation, ordinary kriging, and inverse distance weighting, have been widely used for spatializing air temperatures observed at meteorological stations, and these methods can also be used to reconstruct LST. Wu et al. ^[35] selected patches without invalid values from FY-2G LST in China and MSG-SEVIRI LST in Europe and masked the LST with different missing data rates and different distribution characteristics to simulate various cloudy conditions. Then, the spline method was applied to fill the missing LST values. The average root mean square error (RMSE) of the FY-2G was 1.1 K, and that of the MSG-SEVIRI was 1.7 K. The above spatial interpolation method is only based on the spatial proximity between pixels and does not include any additional auxiliary factors that affect the spatial distribution of LST. The method is not suitable for large-scale areas or those with high spatial heterogeneity. Moreover, with an increase in the cloud cover amount or the concentration of cloud cover, the reconstruction accuracy obviously declines. Therefore, simple spatial interpolation is not a good choice for reconstructing LST in areas with dense or large cloud covers.

The elevation is an important factor that affects the spatial distribution of surface temperature ^[36] and is therefore often employed as a covariate in spatial regression to improve the gap-filling performance for remotely sensed LST. Neteler et al. ^[24] removed outliers in daily MODIS LST from 2000 to 2008 in the central-eastern Alps in Northern Italy according to histograms and temperature gradients and then used the volumetric splines interpolation method with LST and elevation as the input variables to reconstruct invalid LST from the actual map gradients or 16-day mean gradients under the condition of insufficient pixels. The Wilcoxon rank-sum test performed on the station-observed temperature and reconstructed LST curves indicated that they did not differ statistically (W = 63775.50, p-value = 0.62), and the differences between the station-observed and reconstructed annual temperatures were less than 0.5 K. Zhou et al. ^[37] retrieved LST from Landsat7/ETM+ data in Jiangning District, China, and masked some pixels to simulate cloudy regions. By introducing valid spatially neighboring LST and longitude, latitude, and elevation as input variables, the gradient plus inverse distance squared method was applied to estimate the LST in these simulated cloudy regions. The maximum mean absolute error (MAE) and RMSE were less than 0.9 K and 1.2 K, respectively, and the reconstructed LST had lower accuracies in areas with complicated surface or high cloud covers. Ke et al. ^[38] presented an adaptive window-based spatial interpolation algorithm with spatially neighboring valid LST and elevation as the input variables to reconstruct 8-day LST in the Tibetan Plateau by using regression equations between LST and elevation in each sliding window to estimate the LST of the cloudy pixels. Finally, the reconstructed LST of four overpasses were aggregated and compared with air temperatures from meteorological stations. The validation showed that the reconstructed LST was significantly correlated with the observed LST, with an average coefficient of a determination (R²) value of 0.96 and an MAE value of 2.02 K. These results indicated that the method performed well for unevenly distributed invalid LST pixels, but there was some residual noise in the reconstructed LST. The normalized difference vegetation index (NDVI) is a good integrated indicator of land cover, vegetation density, and productivity ^[39] and effectively influences the land surface during surface thermal processes. Ke et al. ^[39] applied the hybrid regression kriging technique to model the spatial pattern of 8-day MODIS LST over the central Qinghai-Tibet Plateau from 2003 to 2010, using latitude, longitude, elevation, and NDVI as the input variables. The original and reconstructed LST were compared with the surface temperature observed at meteorological stations, showing average MAE values of 2.22 K and 1.72 K, respectively.

The spatial gap-filling method is relatively easy to apply. After introducing auxiliary predictors such as elevation and NDVI, reconstruction accuracies can be improved in areas with complicated terrain, which are recommended methods for spatial gap-filling methods. However, under conditions with concentrated clouds or extensive clouds, these methods may fail to achieve satisfying results.

Table 4. Summary of spatial gap-filling methods.

4.2. Temporal Gap-Filling Methods

In temporal gap-filling methods, cloud-contaminated LST values are filled using valid LST of the same pixel at neighboring times. Table 5 provides a summary of temporal reconstruction methods and their validation performances.

Linear interpolation is the most straightforward temporal gap-filling method. This method uses temporal-neighboring valid LST values to calculate missing LST values under cloudy skies. Zhang et al. ^[40] filled the data gaps for the 8-day MODIS LST in northeastern China in 2010 by the temporal linear interpolation method but did not provide any validation of the reconstructed LST. Temporal variations of LST are influenced by many factors and generally show complicated and fluctuating changes. Simple temporal linear interpolations may produce unreasonable estimates with large errors, especially during periods with dramatically changing weather conditions.

Terra/MODIS and Aqua/MODIS acquire data twice daily, and the overpass times of these two satellites are close to each other (~2 h), providing multi-temporal LST observations over a short time interval. Gap-filling by temporal interpolation methods that combine Terra/MODIS and Aqua/MODIS LST can improve the integrity of LST data. Crossen et al. ^[26] calculated the mean difference between the daily Terra/MODIS and Aqua/MODIS LST of each grid over the conterminous United States and then supplemented the Aqua/MODIS LST by adding the Aqua–Terra LST differences to the Terra/MODIS LST. Compared with the original Aqua/MODIS LST, the data coverage of the reconstructed LST was increased by almost 25% during the daytime and 30% during the nighttime. Coops et al. ^[41] developed multiple regression equations for each cover type, period, and granule using Aqua/MODIS LST as the dependent variable and Terra/MODIS LST, latitude, longitude, and elevation as the independent variables. Then, the most suitable equation was applied to produce a seamless Aqua/MODIS LST dataset across Canada. The fitted Aqua/MODIS LST values were compared with the corresponding original Aqua/MODIS LST values, showing R² ranging from 0.91 to 0.97 and standard errors ranging from 3.2 K to 3.3 K. This reconstruction method is dependent on the quality of the Terra/MODIS and Aqua/MODIS LST obtained on the same day and might fail to produce completely gap-filled LST series under a persistent cloud cover.

The diurnal and annual variations in LST are mainly driven by periodic solar radiation and can theoretically be fitted with a series of harmonics. Diurnal temperature cycle (DTC) models and the annual temperature cycle (ATC) models have been developed to simulate temporal variations in temperature ^[42][43]. DTC models are constructed from multi-temporal temperatures recorded over a day; these temperatures are not applied to reconstruct LST but are used to reconstruct bright temperatures under cloudy skies ^[43][44]. ATC models are fitted from multi-temporal temperatures recorded during a year and have been used in LST reconstructions. Xu et al. ^[29] introduced the Harmonic Analysis of Time Series (HANTS) algorithm, which has been widely used for NDVI reconstructions, to reconstruct an annual 8-day MODIS LST series in the Yangtze River Delta, China. A validation, which was conducted based on artificially simulated cloudy pixels, showed an R² value of 0.97 and an MAE value of 1.51 K. The ATC models with relatively sophisticated forms generally have relatively high accuracies but low generalization abilities ^[45] due to their requirements of large numbers of parameters. On the other hand, simple ATC models, such as the ATC models with one or two harmonics, have good generalization abilities but relatively poor fitting performances. Prediction accuracy and generalization ability are often hard to balance in existing ATC models ^[46]. To overcome this limitation, Liu et al. ^[46] proposed a hybrid ATC (ATCH) model for LST estimations; in this hybrid model, multiple harmonics are combined with linear functions of LST-related factors to balance the accuracy and generalization ability of the model. This model was applied to reconstruct MODIS LST in mainland China in 2012. A validation conducted with in-situ LST observations obtained from Surface Radiation Budget Network stations showed average RMSEs value of 2.7 K and 2.1 K for daytime and nighttime, respectively, with reductions of 1.8 K and 0.7 K, respectively, compared with the original sinusoidal ATC model. The paper also masked LST using gaps of different sizes to simulate cloud cover in LST images and compare the performances of the ATCH method and the regression kriging spatial interpolation method. The results indicated that the mean RMSEs of the ATCH model ranged from 2.6 K to 5.1 K and were always lower than those of the regression kriging method (ranged from 3.2 K to 7.0 K). Compared with temporal linear interpolation methods, the harmonic methods based on ATC models usually have better reconstruction performance and work well for areas with longer and larger cloud coverage. However, harmonic curves still have difficulty in fitting sudden temporal changes of LST series, obviously impacting their gap-filling accuracies.

Machine learning, which has great advantages in producing reasonable and robust relationships in the presence of noisy or missing input, has been introduced to reconstruct time series of remotely sensed datasets ^{[47][48][49][50]}. Dictionary learning provides a way to exploit the information from multi-temporal images by removing the redundant parts and has recently been proven to be effective for signal reconstruction in the image processing domains ^[51]. Taking the temporal correlations between multitemporal data into account, Li and Shen ^[52] expanded algorithms based on K-SVD dictionary learning and Bayesian dictionary learning, respectively, to explore a better reconstruction for daily MODIS LST. The validation based on simulated cloud-cover indicated that the expanded methods performed better than HANTS and dictionary learning methods without multitemporal expanded, with MAEs of 0.214 K and 0.467 K for partially cloudy, respectively. Long short-term memory (LSTM) neural networks are a specific type of recurrent neural network in which an input gate, a forget gate, and an output gate are used to control the flow of information through the cell and the neural network. LSTM neural networks can effectively alleviate the vanishing gradient problem, making them suitable for processing complex problems with long-term dependencies. Arslan and Sekertekin ^[53] applied LSTM networks to reconstruct the daily MODIS LST from 2017 to 2019, introducing the first 82% of the data as the training data to fit the model and using the rest of the data as the testing data for validation. A validation showed RMSEs ranged from 2 K to 9 K for daytime LST and ranged from 1 K to 5 K for nighttime LST. Temporal gap-filling methods such as harmonic fitting-based and machine learning-based are well suited for LST reconstructions over large cloud cover areas. However, it is difficult to use these temporal gap-filling methods to describe sudden changes in LST series. Compared with harmonic fitting, machine learning-based methods have greater potentials because they can fitting complicated relationships, especially by introducing ancillary information.

Table 5. Summary of temporal gap-filling methods.

4.3. Spatiotemporal Gap-Filling Methods

Spatiotemporal gap-filling methods integrate the temporal and spatial information of thermal infrared remotely sensed LST, partly addressing the limitations of temporal and spatial gap-filling methods and incorporating the advantages of both. Table 6 provides a summary of spatiotemporal reconstruction methods and their validation performances.

Li et al. ^[30] developed a 3-step hybrid reconstruction method that firstly integrated four daily MODIS LST observations by the merging methods of Coops et al. ^[41] and Crosson et al. ^[26]. Then, the missing values in merged LST were estimated using the R Gapfill package ^[54] for spatiotemporal gap-filling, which constructs a quantile regression based on the LST distribution in the window of adjacent daily images to estimate missing LST values, and the remaining gaps were filled by a temporal interpolation method. This method was applied to reconstruct seamless LST in the conterminous U.S. in 2010, and compared with temporal interpolation and spatiotemporal gap-filling methods, the hybrid method achieved a higher accuracy with an RMSE of 3.35 K. Hassan et al. ^[55][56] proposed a gradient spatiotemporal method for cloud-contaminated 8-day MODIS LSTs. The missing LST is estimated by adding the average temporal deviation for LST of valid pixels to the annual mean LST of each cloud-contaminated pixel and this method was validated with simulated cloud cover in the Atlantic Maritime Ecozone in eastern Canada and achieved an R2 of 0.88. Weiss et al. ^[57] proposed a gap-filling approach for continental-scale remotely sensed LST time series and applied it to the 8-day MODIS LST reconstruction. The first step of this approach is searching the images taken on the given day during adjacent years to obtain a valid value for the corresponding pixel. Then, the pixels that are spatially close to the target pixel are identified within a maximum search radius. If the number of spatially neighboring pixels meets a given threshold, the target LST is calculated using the inverse distance weighting approach. Otherwise, the remaining data gaps are estimated by multiplying the mean ratio obtained from all available neighboring pixels by the value obtained from the mean image of the original gap pixel. This method was validated by introducing artificial cloud cover gaps in an 8-day MODIS LST series in Africa, producing R² values above 0.87. Yu et al. ^[58] proposed a reconstruction method based on approximating the same LST change trend over time between the missing pixel and its similar valid pixel. The images with high data validity are considered as reference images and interpolated by IDW, while the remaining images are gap-filled by LST transfer function of the similar pixel identified by terrain factors (DEM, slope, aspect, NDVI) and solar factors (solar radiation, LST). The method was applied to reconstruct the daily MODIS LST in the Tibetan Plateau and the validation based on ground temperature from meteorological stations produced average RMSEs of 4.27 K and 3.63 K for the daytime and nighttime. Based on the similar pixels method proposed by Yu , Tan et al. ^[59] corrected the theoretical clear-sky LST by estimating the cloud effect on LST, which is related to time, NDVI, and geography. The validation result showed that the reconstructed LST is highly consistent with in-situ measurements, with a mean RMSE of 2.91 K at night and 4.41 K in the daytime, and mean R² of 0.93 at nighttime and 0.90 in the daytime. Pede and Mountrakis ^[60] compared the performances of six gap-filling methods, including the spline, adaptive window, linear temporal, HANTS, gradient and Weiss methods, in filling LST data gaps under various cloud cover conditions based on cloud-simulated 8-day MODIS LST across 85 test sites in the conterminous United States. The comparison results revealed that the spatial methods performed best but were vulnerable to terrain effects, while the spatiotemporal methods performed better than the temporal methods and were less influenced by terrain factors than the spatial methods were. Among the studied methods, the Weiss method generally performed best under greater cloud cover conditions, with MAEs ranging from 0.3 K to 1.2 K, and the spline method performed best under low cloud cover conditions, with MAEs ranged from 0.2 K to 0.6 K; further, the spline method is relatively practical.

The accuracies of spatiotemporal gap-filling methods are dependent on the quality of LST data. Under large-extent and long-term cloud cover conditions, the reconstruction performance worsens due to the complicated and nonlinear relationships that occur across space and time between LSTs obtained from different spatiotemporal geostationary satellites ^[35]. Generally, machine learning models perform better than traditional regression models when handling complicated nonlinear relationships ^[61][62]. In recent years, several studies have introduced different machine learning models for estimating LSTs under cloudy conditions. Sarafanov et al. ^[63] simulated cloudy pixels in Sentinel-3 and MODIS LST data and used lasso regression, random forest (RF), extra trees, support vector regression, and k-nearest neighbors regression methods to gap-fill the LST. In most cases, the errors did not exceed 1 K. Zhao and Duan ^[64] applied the RF approach to reconstruct Terra/MODIS daytime LST in 2015 in southwestern Europe using the vegetation index, normalized difference water index, solar radiation, surface albedo, elevation, slope, and latitude as predictors. The solar radiation derived from the cumulative MSG/SEVIRI downwelling surface shortwave radiation flux recorded from sunrise to the satellite overpass time reflects the impact of cloud cover on the LST and characterizes the difference between the theoretical clear-sky LST and the actual cloudy LST. Therefore, a model developed using LST from clear-sky pixels can be applied to cloudy pixels to estimate actual LST values. Validations with GLDAS LST data and air temperature measurements from meteorological stations produced R² values of 0.73 and 0.75 and RMSE values of 1.66 K and 2.49 K, respectively. Given the superiority of the deep convolutional neural network (CNN) in solving highly nonlinear and dynamic problems, Wu et al. ^[35] proposed a multiscale feature connection CNN model to fill the simulated cloudy pixels in FY-2G and MSG-SEVIRI LST. The average RMSEs of the model in different seasons and different years were mostly less than 0.8 K, and the filling accuracies did not change extensively under various cloudy conditions. In contrast, the average RMSE of the spline spatial interpolation method was mainly approximately 1.1 K for FY-2G LST and 1.7 K for MSG-SEVIRI LST; these errors also increased with higher missing rates or more concentrated cloud distributions. The results of the comparison indicated the good performance of the deep learning method.

The spatiotemporal gap-filling methods are relatively complex, and the theoretical principles of different methods may be distinctly different. A comprehensive validation that applies all these methods in the same study area is needed to compare the performances of these methods.

Table 6. Summary of spatiotemporal gap-filling methods.

4.4. Multi-Source Fusion-Based Gap-Filling Methods

Except for the method by Tan et al. ^[59] and RF-based method by Zhao and Duan ^[64], all the other previously described LST reconstruction methods can only estimate the theoretical cloud-free LST rather than the actual cloudy-sky LST ^[30]. The introduction of surface temperatures from other sources (microwave remotely sensed data or meteorological reanalysis data) has provided a new way to reconstruct LST under cloudy conditions, which can address this limitation to some extent. Recently, integrating surface temperature derived from passive microwave (PMW) or reanalysis temperature datasets to fill data gaps in TIR LST products has provided a new way to reconstruct LST under cloudy conditions.

Generally, TIR-derived LST products have relatively high accuracies and spatial resolutions but are easily influenced by weather conditions ^[65]. In contrast to TIR remote sensing, PMW remote sensing, which can penetrate clouds and rain, provides all-weather observations. Many methods have been developed to retrieve LST from PMW data, including empirical methods ^{[66][67][68][69]}, semi-empirical methods ^[34][70][71], physical methods ^[72][73], and neural network methods ^{[32][74][75][76]}. However, PMW-derived temperature series have relatively poor accuracies and spatial resolutions. The different characteristics of TIR and PMW cause their temperature retrievals to be complementary ^{[66][77][78][79]}. Table 7 provides a summary of multi-source fusion-based reconstruction methods and their validation performances. Kou et al. ^[80] introduced the Bayesian maximum entropy method to merge MODIS LST and AMSR-E LST and validated the results with soil temperature measurements calibrated using an empirical equation between MODIS LST and soil temperature. The merged LST showed an R² of 0.80 but a high RMSE of 11.2 K. The high error can primarily be explained by the fact that the LST and soil temperature differ in quantity. Zhang et al. ^[81] developed a multiple regression model between 10-km AMSR2 brightness temperature and 1-km MODIS LST under clear-sky conditions to downscale AMSR2 LST to 1 km. This method was applied to produce an all-weather LST dataset in northeast China. The comparison with MODIS LST showed mean bias errors (MBEs) of 1.98 K and 1.57 K, and RMSEs of 2.55 K and 1.04 K for the daytime and nighttime, respectively. Duan et al. ^[25] proposed a framework to produce all-weather LST. First, the subsurface temperature was derived from AMSR-E brightness temperature using a physics-based PMW subsurface temperature retrieval algorithm, and then the AMSR-E subsurface temperature was converted to surface temperature and merged with MODIS LST. Finally, the orbital gaps in the AMSR-E temperature were filled by temporal linear interpolation and the inverse distance weighted method. The validation based on in-situ LST measurements at four sites in northwest China showed RMSE values of 3.5–4.4 K for the cloudy pixels. The gap-filling methods in which TIR-derived LST and PMW-derived temperature are merged also have some limitations, including the physical differences between the two temperature measurements, the orbital gaps, and the coarse spatial resolutions of PMW data ^[25]. In addition, there is still a lack of practical, accurate spatial downscaling methods for PMW LST over highly heterogeneous surfaces, especially in urban areas ^[65][82][83].

Meteorological reanalysis data is another source of spatially continuous surface temperature over large scales. Reanalysis datasets have been widely used in weather and climate research ^[84][85][86]. Fu et al. ^[87] used the random forest (RF) algorithm to fit the relationships between MODIS LST and weather research and forecasting model/urban canopy model LST obtained over clear-sky pixels in the Baltimore-Washington metropolitan region. Then, MODIS LST was estimated based on the developed model, and each fully cloud-contaminated image was interpolated using the combined weight from its temporally adjacent images. A validation, which was based on original MODIS LST, showed an RMSE of 1.8 K for partially cloudy images and 2.0 K for fully cloudy images, respectively. Long et al. ^[88] fused the MODIS LST and China Land Data Assimilation System (CLDAS) LST using the enhanced spatial and temporal adaptive reflectance fusion model (ESTARFM) ^[89] and then used a bias correction approach to minimize the differences between the fused LST and MODIS LST to improve the fusion accuracy. Compared with in-situ measurements from three flux towers, the results showed MAEs ranging from 2.20 K to 3.08 K, RMSEs ranging from 2.77 K to 3.96 K, and R² ranging from 0.93 to 0.95. Moreover, there was no significant difference between the accuracies of the fused LST of clear-sky and cloudy pixels on cloudy days. Zhang et al. ^[90] proposed an RTM method to merge daily MODIS LST and GLDAS LST in the Tibetan Plateau during 2003–2014 based on the model of decomposing LST time series. The validation based on in-situ LST showed the RMSEs ranging from 2.03 K to 3.98 K, and the comparison with the fusion method proposed by Long ^[88] indicated that RTM provided higher spatial completeness and data availability. However, the spatial resolution of reanalysis data is usually much coarser than that of TIR-derived LST, and these large spatial scale differences affect the fitting accuracy.

The quality of reanalysis data is highly dependent on the meteorological stations. For the remote areas with sparsely distributed stations and complicated terrain, the accuracy of reanalysis data is generally low, which will also affect the accuracy of reconstructed LST by the reanalysis data-fused method. Compared with reanalysis data, PMW data performs well over areas with complex terrain and sparse stations, which should be a better choice for multi-source fusion-based gap-filling methods. Considering that the multi-source fusion-based method can estimate the actual cloudy temperature, it is the best method in most cases. However, in urban heat island studies, the multi-source fusion-based method may not perform well because the downscaling models are developed at coarse spatial scales and can not effectively depict the detailed spatial difference of LST over urban and suburban areas. The spatiotemporal gap-filling method can perform better in this respect.

Table 7. Summary of multi-source fusion-based gap-filling methods.

4.5. Surface Energy Balance-Based Gap-Filling Methods

In surface energy balance (SEB)-based gap-filling methods, the differences between clear-sky and cloudy-sky pixels are calculated based on the land surface energy balance equation to estimate actual LST under cloudy conditions ^[87]. Table 8 provides a summary of SEB-based reconstruction methods and their validation performances.

Jin ^[91][92] proposed an SEB-based neighboring-pixel (NP) interpolation method to estimate LST under cloudy conditions. This SEB model was applied to calculate the LST differences between cloudy pixels and spatially neighboring cloud-free pixels; these differences were mainly caused by their different radiation inputs and redistributions and were used to interpolate the LST data gaps by spatially neighboring valid LST. The validation based on field experiments and climate community model/biosphere-atmosphere transfer scheme simulation data showed that the general accuracy ranged from 1 K to 2 K on a monthly basis. Lu et al. ^[28] developed a temporal SEB-based NP approach to calculate the LST differences between cloudy pixels and temporally neighboring cloud-free pixels and then reconstructed the diurnal cycle of MSG/SEVIRI LST. The validation based on in-situ measurements from two sites in Africa showed an RMSE of 5.55 K and a bias of –3.68 K in Kenya, and an RMSE of 5.11 K and a bias of 0.37 K in Burkina Faso. Yu et al. ^[93] developed a spatiotemporal NP interpolation to estimate LST over cloudy pixels in daily MODIS LST data in the Heihe River Basin, China. The validation based on in-situ measurements showed an RMSE of 4.12 K and a bias of 0.25 K during the daytime, and an RMSE of 2.90 K and a bias of –0.13 K during the nighttime.

None of the aforementioned SEB-based NP methods take the terrain into account, and this omission affects the accuracy of the reconstruction over mountainous regions with complex topography. Yu et al. ^[94] developed an improved spatiotemporal NP method in which satellite-derived auxiliary data are introduced to reduce the error resulting from input variables. The validation based on in-situ measurements showed an average error less than 1.00 K and an RMSE less than 3.20 K. Zeng et al. ^[31] proposed a two-step framework to reconstruct MODIS LST. In this method, pixels that are similar to each cloudy pixel are screened by referring to the vegetation index and used to estimate LST under cloudy conditions through a weighted linear regression. Then, the relationship between the clear-sky LST and actual cloudy-sky LST, derived from the SEB equation using MODIS albedo, MODIS emissivity, and Global Land Surface Satellite (GLASS) downward shortwave radiation as input variables, was applied to correct the estimated theoretical clear-sky LST to actual LST. The validation based on surface radiation budget observing network (SURFRAD) data showed R² ranging from 0.72 to 0.93 and MAEs ranging from 3.65 K to 6.70 K. Jia et al. ^[95] proposed a generic SEB-based physical method for estimating cloudy-sky LST. The first step is constructing an annual LST dynamic model by downward and upward longwave radiation from ERA5 and broadband emissivity from GLASS, to estimate the theoretical clear-sky LST. Then, the cloud effect on LST is represented by calculating the cloud net radiative forcing on cloudy days, using a multivariate adaptive regression spline model based on SEB theory. The method was applied to VIIRS LST and MODIS LST, and validated using in-situ measurements from SURFRAD sites. The validation exhibited an RMSE of 3.54 K, an R² of 0.94 for VIIRS LST, an RMSE of 3.69 K, and an R² of 0.93 for MODIS LST.

The introduction of satellite radiation products instead of ground-based measurements reduces the reconstruction errors caused by the uncertainties of the input variables, and improves the generalizability and reliability of the SEB-based methods.

Table 8. Summary of SEB-based gap-filling methods.

5. Validation of Reconstructed LST

Reasonably evaluating the accuracy of filled LST values is of great significance for LST reconstructions. However, due to the difficulty of obtaining actual LST at large scales, existing studies have used reference datasets from different sources to validate filled LST values, including artificially simulated cloud-contaminated LST datasets, station-observed LST, meteorological station-observed temperature, and from PMW or reanalysis datasets.

5.1. Validations Based on Artificially Simulated Cloud-Contaminated LST

Simulated cloud-contaminated LST is produced by artificially masking some cloud-free pixels in remotely sensed LST. Taking these masked pixels as cloudy areas, reconstruction methods are applied to estimate the LST values of the masked pixels, and the estimated LST values are compared with the original values to indicate the reconstruction performance ^{[29][35][37][60][63]}.

This validation method is simple and feasible to implement. Moreover, it can simulate different cloudy conditions by modifying the proportions and spatial patterns of the masked pixels. However, the most important limitation of this method is that the LST values of the simulated cloudy pixels are not actual LST under cloudy conditions but theoretical clear-sky LST. The direct driving force of LST is solar radiation, and solar radiation under cloudy conditions is quite different from that under clear-sky conditions. Therefore, the validations based on simulated datasets cannot accurately characterize reconstruction performances for actual cloudy regions.

5.2. Validations Based on Ground-Observed LST Data

Ground-observed LST data is generally derived from measurements recorded in flux stations or field research; these are the only sources that can provide accurate point-scale LST data for validations. Station-observed LST is employed to validate reconstructed remotely sensed LST ^{[26][31][46][88][94]}.

LST cannot be directly observed and instead is calculated from some measured radiation parameters. The measurement stations observe surface upwelling longwave radiation, atmospheric downwelling longwave radiation, and surface broadband emissivity and then calculate LST based on the Stefan–Boltzmann law:

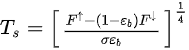
where \( T_s \) is the LST, \( F^\uparrow \) is the surface upwelling longwave radiation, \( F^\downarrow \) is the atmospheric downwelling longwave radiation, \( \sigma \) is the Stefan–Boltzmann constant (\( 5.67 \times10^{-8} \cdot W\cdot m^{-2}\cdot K^{-4} \)), and \( \varepsilon_b \) is the surface broadband emissivity.

Due to the limited number of flux stations, generally, only a few stations can be used, preventing the effective representation of various cloud conditions. In addition, point-scale validation data have poor spatial representation at the pixel scale in heterogeneous environments, especially when used in coarse-resolution LST validations.

5.3. Validations Based on Meteorological Station-Observed Temperature Data

The meteorological stations are common sources to collect temperature data; these stations provide long-term reference data for validations. Generally, meteorological stations measure air temperature and soil temperature, not LST. Air temperature and soil temperature measurements collected from meteorological stations have also been used for validations ^{[24][38][39][64][80]}. However, although there are strong relationships among air temperature, soil temperature, and LST, these three temperature measurements have different physical meanings. Therefore, air temperature and soil temperature can be used only for indirect validations, such as correlation or consistency analyses. Some studies ^[24][64] have investigated the consistency between station-observed air temperature and reconstructed remotely sensed LST to validate the LST gap-filling performance in cloudy regions. However, the relationship between LST and air temperature varies with the seasonality, elevation, and terrain roughness ^[96]. Some studies ^[38][39] used 0-cm soil temperatures from meteorological stations to validate reconstructed LST. Considering that the physical meaning of soil temperature also differs from that of LST, studies were carried out to fit empirical relationships between soil temperature and remotely sensed LST, and then adjusted soil temperature to LST for validation ^[80]. Compared with flux stations, there are many more meteorological stations, and meteorological stations can cover various climate zones and cloudy conditions. Even so, the distributions of meteorological stations are sparse and uneven in high-altitude or remote areas, making the validation of LST reconstructions highly challenging in these areas.

5.4. Validations Based on Gridded Temperature Data from Other Sources

The gridded temperature data obtained from other sources for evaluating reconstruction performance include TIR-derived LST from other sensors ^[26][41][87] and reanalysis temperature data ^[64][91][92]. When there is a lack of ground-based data, these validation methods are commonly used.

Due to the different instrument characteristics and production methods of these data, there are uncertainties when directly comparing the LST obtained from these other sources with TIR LST. Some studies have compared the consistency between these datasets, and some studies have adjusted the LST obtained from other sources to TIR LST for validation.

6. Conclusions and Perspectives

This paper outlines the progress of LST reconstruction under cloudy conditions, including four parts: analysis by bibliometrics, temperature data used for reconstruction, reconstruction methods and validations. The number of published papers on LST reconstruction shows an obvious increasing trend since 2010, indicating that this topic has become a research hotspot. Wu et al. ^[97] have published a review paper on LST reconstruction in February 2021. Compared with this paper, our paper summaries the progress of LST reconstruction from different perspectives, including different classifications of existing methods, different discussions, and different outlooks for the future. In addition, our paper also includes some latest published papers. The two papers are complementary to provide researchers with guidelines.

The existing reconstruction methods can be grouped into five categories: spatial gap-filling methods, temporal gap-filling methods, spatiotemporal gap-filling methods, multi-source fusion-based gap-filling methods, and SEB-based gap-filling methods. Spatial gap-filling methods and temporal gap-filling methods are relatively simple and easy to implement. However, spatial gap-filling methods do not perform well in regions with large cloud coverage. Temporal gap-filling methods work relatively well for areas with large cloud coverage but cannot fit sudden variations in LST. Spatiotemporal gap-filling methods combine the advantages of the above two methods by integrating temporal and spatial information; these methods require multidimensional input information. SEB-based gap-filling methods are based on the physical mechanism of the surface energy balance to estimate the actual LST but require many environmental variables and are sensitive to the quality of the input parameters, which limits the application of SEB-based methods. Most of the above methods suffer from a major limitation in that the filled LST values in cloudy pixels represent theoretical LST under cloud-free conditions. Multi-source fusion-based gap-filling methods merge TIR-derived LST with PMW-derived LST or reanalysis LST to produce actual all-weather LST; these methods can generate actual cloudy LST, which may not be superior in validation accuracy but better match to the actual surface situation. The quality of reanalysis data is highly dependent on the meteorological stations. For the remote areas with sparsely distributed stations and complicated terrain, the accuracy of reanalysis data is generally low, which will also impact the accuracy of reconstructed LST by the reanalysis data-fused method. Compared with reanalysis data, PMW data performs well over areas with complex terrain and sparse stations, which should be a better choice for multi-source fusion-based gap-filling methods. Multi-source fusion-based methods have to overcome the challenges of coarse spatial resolutions, different observation times, and differences among multisource LST datasets. Each method has its own advantages and disadvantages. Due to the differences in geography and climate conditions of different study regions, the accuracies of obtained results of different studies cannot be compared directly. However, the performances of different methods under various conditions can be discussed. Table 9 gives the applicability of each method under different weather and surface conditions.

Table 9. Applicability of each gap-filling method under different conditions.

Accurately reconstructing LST is challenging but meaningful, and all currently available methods still have limitations. In the upcoming years, machine learning techniques that have advantages in fitting complicated relationships will be more widely used in LST reconstruction, especially in multi-source fusion-based gap-filling methods. In addition to cloud mask or cloud cover fractions that are commonly used in reconstructing LST, cloud properties, including cloud type, cloud top temperature, and cloud height could be employed as auxiliary information to improve LST reconstruction accuracy. Most of the existing methods are applied to reconstruct 8-day LST or daily MODIS LST. In the future, LST from geostationary satellites should be used to produce all-weather LST datasets with higher temporal resolution. As the reconstruction needs at spatial coverage, spatial resolution, and temporal resolution, the data size and computational costs required for LST reconstruction grow rapidly. Mainstream computing platforms will gradually transfer from local computing to online cloud-based platforms that provide massive computational capabilities, such as Google Earth Engine, Google Colaboratory, and Amazon Web Services.

Due to the difficulty of obtaining LST observations, the lack of consistent and reliable LST validations data hinders validations of LST reconstruction under cloudy conditions. Artificially simulated cloud-contaminated LST, which is widely used for validations, cannot reflect the influence of cloud cover on the actual LST. Ground-observed LST is usually available from a limited number of flux stations or field research. Meteorologically observed soil and air temperatures cannot be directly compared with remotely sensed LST. Gridded temperature data obtained from other sources have limitations such as coarse spatial resolutions and uncertain differences between the gridded datasets and TIR-derived LST. Carrying out reliable validations of reconstructed LST is still a problem that needs to be further explored.

This entry is adapted from the peer-reviewed paper 10.3390/rs13142838