This review discusses molecular adducts, whose composition allows a symmetric structure. Such adducts are popular model systems, as they are useful for analyzing the effect of structure on the property selected for study since they allow one to reduce the number of parameters. The main objectives of this discussion are to evaluate the influence of the surroundings on the symmetry of these adducts, steric hindrances within the adducts, competition between different noncovalent interactions responsible for stabilizing the adducts, and experimental methods that can be used to study the symmetry at different time scales. This review considers the following central binding units: hydrogen (proton), halogen (anion), metal (cation), water (hydrogen peroxide).
1. Introduction
If something is perfectly symmetric, it can be boring, but it cannot be wrong. If something is asymmetric, it has potential to be questioned. Note, for example, the symmetry of time in physics [1,2]. Symmetry also plays an important role in chemistry. Whether it is stereochemistry [3], soft matter self-assembly [4,5], solids [6,7], or diffusion [8], the dependence of the physical and chemical properties of a molecular system on its symmetry is often a key issue. Symmetric molecular adducts are popular model systems; they are used to analyze the effect of structure on the property chosen for research since they allow one to reduce the number of parameters [9,10,11,12]. On the other hand, symmetry in chemistry is a matter of the size and time scale in question [13]. The same molecular system can be symmetric for one experimental method and asymmetric for another. It is important to understand what processes are hidden behind this discrepancy in each specific case.
The problem of the size scale already begins at the level of the model adducts composition. What structure has the simplest model adduct with which it is possible to investigate the property under consideration? The Zundel cation (H5O2+) and the Eigen cation (H9O4+) seem to be the most illustrative example [14,15]. Which of these two structures is the best for simulating a hydrated proton? It seems that neither experiment nor theory can answer this question regardless of the property being discussed [16,17,18,19,20]. The same is valid for the hydration of the hydroxide ion [21,22,23,24]. Of course, bulk water is one of the most complex solvents in this content. The time scale problem has to do with tautomerism. For some methods, its rate is slow. In this case, experimental parameters can be observed for each of the structures presented. For other methods, this rate is fast and only average experimental parameters can be observed.
2. Hydrogen (Proton) as the Binding Unit
2.1. Intramolecular H-Bonds
Figure 1 shows selected molecules with an intramolecular H-bond. The lowest energy geometry of 3-carboxypropanoate (the maleate anion,
Figure 1a) in the gas phase has an asymmetric H-bond. The OH and H···O distances are 1.33 and 1.10 Å [
33]. However, the zero-point energy is above the energy barrier for proton transfer. Consequently, due to the motion of the mobile proton in the ground vibrational state, the H-bond is symmetric [
34]. As a result, this molecule yielded a broad and featureless photoelectron spectrum [
33].
Figure 1. Potentially symmetric structures with intramolecular H-bonding. 3-carboxypropanoate (a), 2-carboxybenzoate (b), 1,8-bis(di-R-amino)-naphthalene-H+ (c), 1,8-naphthyridine-H+ (d).
The symmetry of the maleate anion in solution was studied using a primary H/D isotope effect on the NMR chemical shift,
pΔ(H/D) ≡ δ(A
DB) − δ(A
HB). The motion of the binding hydron within a H-bond should always be treated as quantum [
35]. Consequently, when the mobile proton is substituted for deuteron, the geometry of the H-bond changes. For a symmetric H-bond this substitution results in a contraction of the heavy nuclei distance, that is, the strengthening of the H-bond; for an asymmetric H-bond it causes a lengthening of this distance, that is, the weakening of the H-bond [
36]. These geometric changes lead to chemical shift changes. It is expected that
pΔ(H/D) > 0 for symmetric H-bonds and negative for asymmetric ones (note, that other authors may define the isotope effects as δ(AHB) − δ(ADB)) [
37]. For the maleate anion
pΔ(H/D) = 0.08 ppm at 150 K [
38] in an aprotic, highly polar CDF
3/CDF
2Cl mixture [
39] and 0.03 ppm at 218 K in CD
2Cl
2 [
40]. These results suggested that under these conditions this H-bond is symmetric. This conclusion was challenged by an
18O-induced isotope shift [
41]. This study claims that such H-bonds in solution are asymmetric due to the anisotropy of the local solvation environment [
42]. This claim seems to be correct [
43,
44]. Chemical shift is a tensor. The discussed experiments in solution operate with the average values of the corresponding tensors. The dependence of the tensors on the H-bond geometry can be complex [
45]. Although the positive sign of
pΔ(H/D) indicates a very strong H-bond, it does not necessarily mean that the bond is symmetric [
46,
47]. It would be interesting to see a detailed analysis of this effect for maleate anion. Moreover, this anion is present in solution together with a cation [
48]. Their interaction can only be neglected in water due to the dissociation of the ion pair. On the other hand, the solvation of the two C=O moieties of the maleate anion by water is symmetric only on average due to a rapid change in the structure of the solvation shell caused by the thermal motion of solvent molecules. In organic solvents the anion–cation interaction cannot be neglected. It is reasonable that, with the exception of very bulky cations, it is this interaction that will determine the symmetry of the H-bond. For the bulky cations, the solute–solvent interactions become critical again. The effect of such interactions on the geometry of H-bonds should not be underestimated [
49]. It is likely that at any given moment of time the H-bond in the maleate anion is asymmetric in any solvent and that its C=O moieties play an important role in this. Note that the intramolecular H-bonds of hydrogen succinate, meso-/rac-2,3-dimethylsuccinate, and (R)-(+)-methylsuccinate are asymmetric in CDF
3/CDF
2Cl [
50].
Similar results have been obtained for hydrogen phthalate,
Figure 1b. Its intramolecular H-bond is symmetric in the gas phase [
60]. In solution it becomes asymmetric due to solute–solvent and anion–cation interactions [
60,
61,
62,
63]. The symmetry of the intramolecular H-bond in 1,8-bis(dimethylamino)naphthalene-H
+ (
Figure 1c) has been recently discussed in detail [
69]. This molecule is the simplest representative of proton sponges, which are a certain type of aromatic diamines with unusually high basicity [
70,
71]. It is also the most studied molecule of this type. The distance between the nitrogen atoms of 1,8-naphthyridine (2,2′-bipyridine) is too large to form a strong intramolecular H-bond,
Figure 1d. In the gas phase [
91], on silica surfaces [
92], and in many crystals it occurs in the
trans-configuration [
93,
94]. Coordination to a metal [
95,
96] or protonation [
97] are required to stabilize the
cis-configuration shown in
Figure 1d. This
cis-configuration of 1,8-naphthyridine-H
+ has been used to study in detail the counterion effect on intramolecular H-bonds and proton transfer using
1H and
15N NMR at 150-115 K in CDF
3/CDClF
2 [
98].
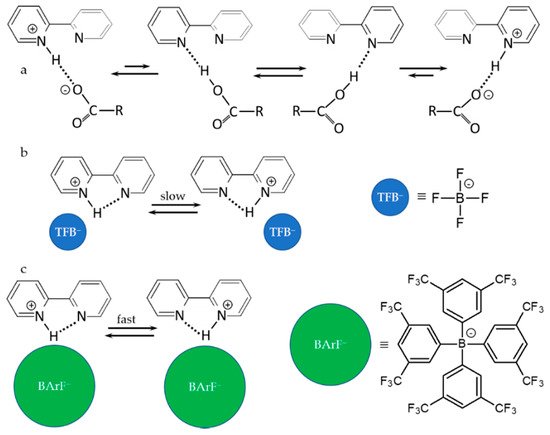
Figure 2 shows the main results of this study.
Figure 2. Anion–cation interactions, H-bonds and proton transfer in 1,8-naphthyridine-H
+ anion complexes in an aprotic polar solvent [
98]. Anions: dichloroacetate (
a), tetrafluoroborate (
b), and tetrakis[3,5-bis- (trifluoromethyl)phenyl] borate (
c).
2.2. Proton-Bound Homodimers
Proton-Bound Homodimers
The question “What factors determine whether a proton-bound homodimer has a symmetric or an asymmetric hydrogen bond?” was answered for homodimers of the [XHX]
+ type in [
99,
100]. It was shown that the symmetry of such homodimers depends on the electronegativity of the atom X. “A more electronegative X atom tends to produce a more positively charged shared proton, which in turn facilitates the closer approach of the two X atoms and the formation of a symmetric hydrogen bond” [
99]. In the gas phase, the symmetric [X···H···X]
+ homodimers are expected for X = F and, with some exceptions, O and sp-hybridized N. For X = sp
2- and sp
3-hybridized N such homodimers will be asymmetric, although proton transfer within such H-bonds can be fast. Proton-bound homodimers involving second-row atoms were studied as well [
101]. Note that the calculation result can critically depend on the level of approximation [
102]. High level calculations can show very good agreement with experimentally observed values [
103,
104,
105].
In condensed matter, various noncovalent interactions compete with each other. Very specific conditions are required to observe centrosymmetric [X···H···X]
+ complexes. For example, it can be noble-gas (Ng) matrices, X = Ng [
106,
107]. The only complex for which the presence of a centrosymmetric structure was experimentally proved in various solvents and solids is [F···H···F]
- [
108,
109,
110,
111].
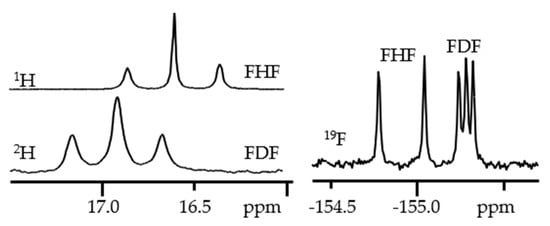
Figure 3 shows
1H,
2H, and
19F NMR spectra of a solution containing the [FHF]
- and [FDF]
- anions and the tetrabutylammonium cation in CDF
3/CDF
2Cl at 130 K [
38].
Figure 3. 1H,
2H, and
19F NMR spectra of the [FHF]
- and [FDF]
- anions and the tetrabutylammonium cation in CDF
3/CDF
2Cl at 130 K [
38].
Nitrogen-containing heterocycles are probably the most experimentally studied proton-bound homodimers of the [X···H···X]
+ type. More specifically, these are symmetrically substituted pyridine derivatives. There are several reasons for this. The basicity of such derivatives can be varied over a wide range in small steps.
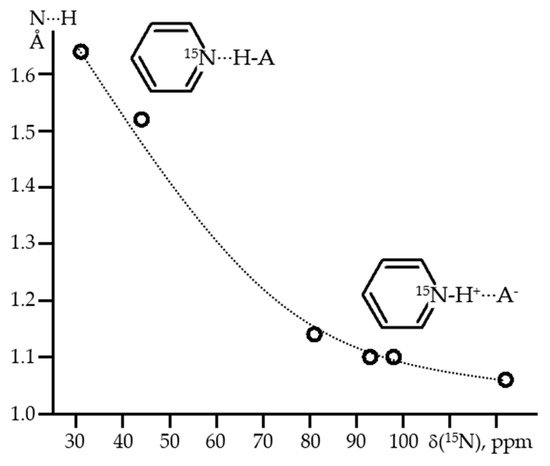
Ortho-substituents can be used to protect the mobile proton from competing interactions, that extends the lifetime of such homodimers. It is easy to switch from homo- to heterodimers to study asymmetric H-bonds. The last, but not least, reason is that H-bonded complexes of pyridines are ideally suited for their NMR study, since one is not limited to
1H NMR. The isotropic
15N NMR chemical shift, δ
iso(
15N), of such pyridine derivatives characteristically depends on the N…H distance [
124,
125,
126]. For all of them, if δ
iso(
15N) ≡ 0 in the absence of H-bonding, δ
iso(
15N) ≈ 125 ppm for the protonated base [
127]. Due to this, for H-bonds of medium strength, the δ
iso(
15N) values can be converted to N…H distances with high accuracy,
Figure 4 [
128]. This correlation has been successfully applied to measure H-bond geometries in solution [
129,
130], interfaces [
131,
132], enzyme environments [
133,
134], and solids [
135,
136].
Figure 4. The average experimental N···H distances of H-bonded pyridines as a function of δ
iso(
15N) [
128].
In the gas phase, the proton-bound homodimer of pyridine has an asymmetric [N···H-N]
+ H-bond [
99]. The N…N distance is about 2.69 Å [
137] and the bond dissociation energy is 105 [
138] or 109 kJ/mol [
139]. In solution, the N…N distance shortens to 2.62 Å [
140] and the bond dissociation energy in CD
2Cl
2 is about 15 kJ/mol [
139]. The geometry of this H-bond is temperature dependent. Cooling leads to an increase in the polarity of the solvent, which causes an increase in the H-N distance and a reduction of the N···H and N.N distances.
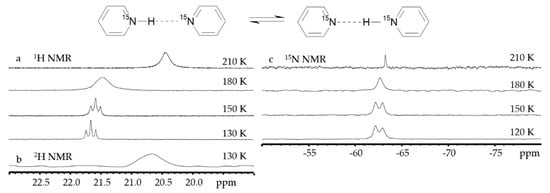
Figure 5 shows NMR spectra of the proton-bound homodimer of pyridine in solution down to 120 K [
141].
Figure 5. 1H (
a),
2H (
b), and
15N (
c) NMR spectra of [pyridine-H(D)···pyridine]
+ in CDF
3/CDF
2Cl at different temperatures. [
141].
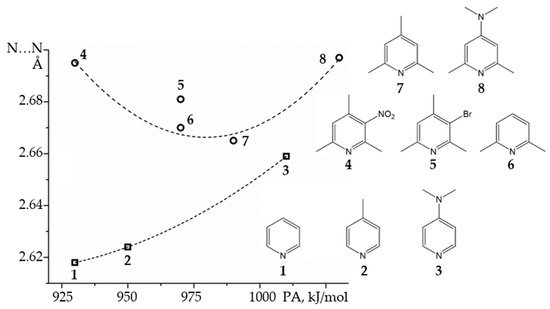
How short can be the N…N distance in the proton-bound homodimers of pyridines? The binding energy of such homodimers will reach a maximum at a certain value of the proton affinity of the involved pyridine derivative [
100].
Figure 6 shows experimental N…N distances in the proton-bound dimers of
ortho-unsubstituted and
ortho-methyl substituted pyridines in CDF
3/CDF
2 at 120K as a function of calculated gas-phase proton affinities [
137,
140]. The N…N distance clearly correlates with the gas-phase proton affinity.
Figure 6. Experimental N…N distances in the proton-bound dimers of pyridines as a function of calculated gas-phase proton affinities (PA) [
137,
140]. The dotted lines are for eye guidance only.
3. Halogen (Anion) as the Binding Unit
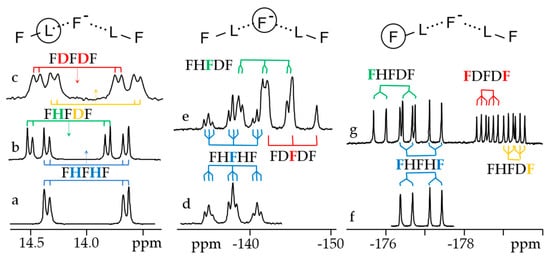
Figure 7 shows 1H, 2H and 19F NMR spectra of solutions containing FH···F-···HF, FH···F-···DF and FD···F-···DF anions in CDF3/CDF2Cl at 130 K [203]. The protons of FH···F-···HF are located at the outer fluorine atoms. The corresponding spin–spin scalar coupling 1JHF = 354 Hz. The protons also couple to the central fluorine atom across the H-bonds, hJH···F = −24 Hz. Therefore, these protons give rise to a doublet of doublet signal, Figure 7a. The outer and central fluorine atoms couple to each other, 2hJF…F = 147 Hz, and give rise to a doublet of doublet signal, Figure 7f, and a triplet of triplet signal, Figure 7d. The rate constant for proton and H-bond exchange is less than 103 s−1. This complex is not linear, the FFF angle is about 130° [191]. There is an anti-cooperative coupling of these two H-bonds. As a result, the FH···F-···DF anion is asymmetric. The 1H NMR chemical shift of the FH···F- proton is larger than the 2H NMR chemical shift of the F-···DF deuteron. The former is also larger, and the latter is less than the 1H NMR chemical shift of the protons in FH···F-···HF (see the arrows in Figure 7b,c). Consequently, the FH···F- H-bond is shorter and the F-···DF one longer than the bonds in FH···F-···HF. This conclusion is confirmed by changes of the coupling constants and 19F NMR chemical shifts. For example, in FH···F-···DF, for the FH···F- H-bond 1JHF = 348 Hz, hJH···F = −22 Hz and 2hJF…F = 151 Hz, while for the F-···DF H-bond 2hJF…F = 140 Hz.
Figure 7. Experimental NMR spectra of solutions containing the FH···F
-···HF, FH···F
-···DF and FD···F
-···DF anions in CDF
3/CDF
2Cl at 130 K [
203]. (
a,
b)
1H NMR, (
c)
2H NMR, (
d–
g)
19F NMR. Arrows indicate the
1H and
2H NMR chemical shifts.
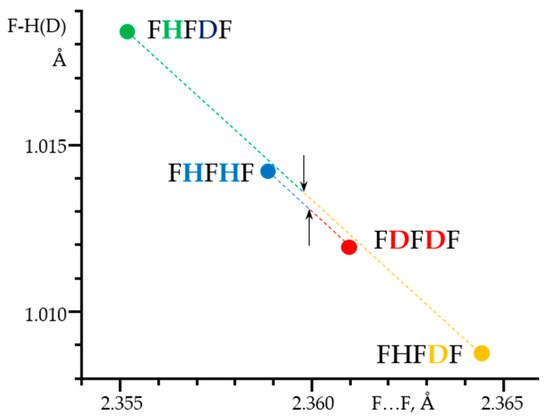
A detailed analysis of the experimentally obtained NMR parameters made it possible to measure the geometry of these H-bonds,
Figure 8. Surprisingly, the resulting effect of the double deuteration corresponds approximately to the algebraic sum of the direct and the vicinal isotope effects [
203]. These sum rules are valid for NMR parameters as well as for the F…F distances.
Figure 8. The F-H(D) distances in the F-H···F
-···H-F, F-H···F
-···D-F and F-D···F
-···D-F anions in CDF
3/CDF
2Cl at 130 K as a function of the corresponding F…F distances. [
203]. Arrows indicate the midpoints of the sums of the F
-…F distances in F-H···F
-···D-F, R
HD = (F
-…F(H) + F
-…F(D))/2, and in F-H···F
-···H-F and F-D···F
-···D-F, R
HHDD = (F
-…F(H) + F
-…F(D))/2.
4. Metal (Cation) as the Binding Unit
Symmetric transition metal organometallics are not necessarily the most effective catalysts. However, the elucidation of their structure in solution can be greatly facilitated if they are or can be symmetric. Although 1H and 13C NMR are not always sufficient to determine the structure of organometallic species, 31P NMR can be very useful when phosphorous is coordinated to the metal center. Only 1,3,5-triaza7-phosphaadamantane (PTA, Figure 9) complexes will be considered here. The rationale for this choice is explained as follows. The 31P isotope is the only stable isotope of phosphorus. It has a spin quantum number of 1/2 and a wide chemical shift range of about 400 ppm. This nucleus is a very convenient NMR probe for studying molecular complexes [99,204,205,206], organometallics [207,208,209,210], and mobility at interfaces [211,212,213]. For example, 31P NMR has been used to study the effect of temperature and hydration on the mobility of small to bulky molecules loaded onto mesoporous silica [214]. However, 31P NMR shielding can depend on the conformation of the molecule [215], the crystalline electric field [216], while various noncovalent interactions can cause similar changes [217].
Figure 9. Selected transition metal complexes of PTA (a): M(PTA)4 (M = Ni, Pd, Pt, Cu+) (b), cis-Cl2M(PTA)2 (M = Ni, Pd, Pt) (c), trans-Cl2M(PTA)2 (M = Ni, Pd, Pt) (d).
5. Water (Hydrogen Peroxide) as the Binding Unit
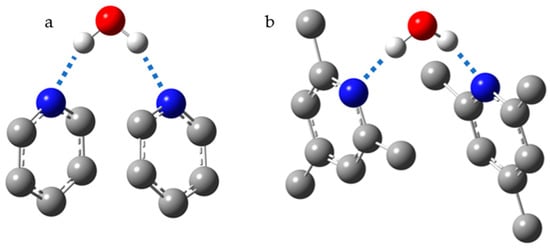
Figure 10 shows the structure of 2:1 pyridine:water and collidine:water complexes, where collidine stands for 2,4,6-trimethylpyridine. In these complexes, the experimentally measured N···H distances are 1.82 Å for pyridine and 1.92 Å for collidine [
237]. The basicity of collidine is higher than that of pyridine. Consequently, the greater distance is the result of steric interactions of the
ortho-methyl groups in the 2:1 collidine:water complex. Indeed, in 1:n base:water complexes, where n >> 1, the experimentally measured N···H distances are 1.69 Å for pyridine and 1.64 Å for collidine. The strong shortening of the distances in both cases is the result of the anticooperative interaction of H-bonds in the 2:1 base:water complex and the cooperative interaction of H-bonds in water clusters.
Figure 10. The most energetically favorable structures for 2:1 pyridine:water (a) and collidine:water (b) complexes.
6. Conclusions
The possibility of being something does not guarantee the ability to actually become that. Molecular adducts, whose composition allows a symmetric structure, can actually be symmetric, symmetric on a certain time scale, or asymmetric. Analysis of this symmetry in a given system can be used to assess its properties and interactions with the environment. Only a few types of such molecular systems are considered in this review. These examples reflect the most important aspects of symmetric molecular adducts:
- (i)
-
Steric hindrance and structural rigidity are not the only reasons why complexes can be asymmetric in the gas phase.
- (ii)
-
At any given moment of time, the solvation shell is somewhat asymmetric.
- (iii)
-
Dynamic processes in crystalline solids can be facilitated if the initial and final states are equivalent.
- (iv)
-
The motion of the proton in a H-bond should always be treated as quantum.
The reader may find it useful to refer to other recent publications on the interactions of tetrahedral pnicogen and tetrel centres with Lewis bases [
248], the coordination of triel centers [
249], tetraphosphido complexes [
250], dinuclear metal hydride complexes [
251], crystalline peroxosolvates [
252], the self-association of phosphonic acids [
253], intramolecular H-bond dynamics [
254], and a consistent description of noncovalent interactions [
255].
This entry is adapted from the peer-reviewed paper 10.3390/sym13050756