1. Introduction

Coastal structures, such as seawalls and breakwaters, provide protection from the effects of the sea and create the conditions for economic growth in coastal environments. These maritime structures also protect ports and coasts against sea dynamics, and their function will be even more important in the upcoming years due to sea level rise and coastal regression as a result of global warming ^[1]. Regarding maritime structures and nearby environments, the effects of sea level rise will include: increasing levels of sediment transport and erosion, higher impacts of wave energy on structures, the loss of stability, and increasing overtopping events ^[2]. On the other hand, increased maritime traffic and human activities along coasts make the proper study and modelling of wave–structure–seabed interactions indispensable in achieving a balance between human intervention, costs, and environmental impacts.

The design of maritime structures must satisfy the project requirements against wind-wave actions ^[3][4] during the structure service life. The uncertainty in maritime structure design increases when its environment is also considered, especially the seabed, which is the foundation of the breakwater. Some structure failure examples due to seabed failure have been reported in the literature ^[5][6]. In fact, historical studies reveal that scour is one of the main reasons behind the failure of coastal maritime structures, such as seawalls, groynes, breakwaters, revetments, and artificial reefs ^[7][8].

Sediment transport has been the subject of extensive research over recent decades, particularly wave–structure interactions and, more importantly, their effects on the seabed. It includes mechanical models ^[9][10], analytical solutions of wave–structure–seabed interactions ^[11][12][13], and their verification with numerical models and experimental tests. Physical models of laboratory experiments face very serious problems with sediment and wave scale, even when the prototype with the Froude scale in a laboratory is well achieved. Despite the problems and issues that still arise in the experimental testing of the seabed response, several studies have investigated sediment transport and the scour around maritime structures.

Numerical models appear to be a valuable tool in designing protective structures and performing parametric studies because of the prohibitive cost of field and laboratory experiments. Numerical modelling requires an integral method that incorporates the processes and effects (displacement, stresses, pressures, etc.) between the wave, seabed, and maritime structure. Few numerical models address sediment transport at scales of practical engineering interest or consider multiphase effects and coupled interaction responses. This is usually attributed to either the lack of understanding of the underlying physics or to the fact that multi-scale physics become too computationally and time expensive when dealing with problems at a practical scale.

Several review papers on sediment transport and seabed response have been published; the topics include: (i) analytical formulas for calculating the scour depth around piers ^[14][15], (ii) analytical and experimental studies of scour around coastal structures ^[16][17], and (iii) However, given the great progress made in numerical modelling in the last decade, there is a need to put the most widely used numerical approaches for modelling the wave–structure–seabed interactions into context and focus. For example, for the swash zone, situated at the landward edge of the inundated part of a coastal region, or for numerical simulations of near-shore regions (where the water depth is much smaller than the wavelength, h/L << 1), the use of depth-averaged models that are based on the Shallow Water Equations (SWE) ^[18] allow for modelling short wave events and studying the morphological evolution of the coastal zone ^[19], and the scour and deposition around structures ^[20][21]. In the seabed response and sediment transport around maritime structures, the models that are based on RANS equations give an adequate description of the wave–structure interactions, as well as the turbulent flow and bottom boundary layer.

2. Damage to Structures and Coastline: The Role of Scour

This section includes a description of the seabed response, scour, and the consequences on maritime structures and coastlines. In addition, the wave–structure interactions processes that induce sediment transport around structures are discussed.

The presence of the protection structure changes the flow patterns in its immediate vicinity, inducing wave reflection and breaking, turbulence, and liquefaction ^[22]. These processes increase the fluid shear stress at the bottom (\( \tau_{f,b} \)) and cause transport when a critical value (\( \tau_{cr,s} \)) is reached. Increased local sediment transport leads to one of the greatest problems for coastal regions and marine structures: scour ^[23][24]. Scour around coastal structures is the additional erosion that takes place due to hydrodynamic forces acting on the seabed.

Scour has significant impacts on the economic and service life of many coastal structures ^[25]. When scour undermines the structure, it cannot support the armour layer of a breakwater, which then slides and loses the fill material. Scour also impacts vertical-front caissons of breakwaters and other gravity structures. More details on scour around such structures can be found in the textbooks of Whitehouse ^[24] and Sumer and Fredsoe ^[22].

Damage to structures is not the only consequence of seabed scour. In fact, the presence of coastal structures can accelerate the erosion (and deposition), thus degrading coastlines ^[26][27][28]. These examples of structural collapse or a loss of material along the coastline result from both transformation and interaction processes between marine dynamics, especially waves, and the coastal structure.

To properly design maritime protection structures and predict the final response of the seabed, it is necessary to identify the physical processes contributing to the scour. A state-of-the-art review on scour processes has been presented in Sutherland et al. [19], Whitehouse [36], Sumer and Freds e [41], Sumer et al. [42]. The reviewed works complement and extend considerably the understanding of the governing processes for certain structures. According to these references, the processes leading to scour are (acting singularly or in combination):

(A) Wave reflection: sediment transport due to wave reflection is perhaps the most commonly cited process in structure–seabed interactions ^[33]. The presence of a maritime structure transforms the incident wave energy into reflected energy, which is returned to the sea. This process involves an increase in wave height and wave energy, in front of the structure, i.e., greater shear stresses on the seabed and, thus, sediment transport.

(B) Wave dissipation: when waves impact a coastal structure, part of its incident wave energy is dissipated by: (a) wave-breaking on the slope or wall, (b) turbulent interactions (circulation and friction) with the armour layer, and (c) wave propagation through the porous media of the structure ^[36]. Among these, wave-breaking on the wall or slope mainly affects sediment transport, which generates turbulence in front of the structure and then mobilizes sediment.

(C) Wave diffraction and refraction: when waves interact with an obstacle or coastline, part of the incident energy is concentrated or dispersed in a certain direction, which induces variations in the wave height and flow velocity, causing non-uniform erosion or sediment deposition ^[29][30]. Furthermore, waves that interact with submerged breakwaters are reduced by a number of energy dissipation mechanisms, including wave breaking and frictional dissipation ^[31][32], which can cause sediment transport around these structures.

(D) Turbulent flow around the structure: the flow contraction and velocity field generate turbulence and vortexes around and in front of the structure, which increase the bottom shear stresses (\( \tau_{f,b} \)) and sediment mobilization ^[22][33]. Some figures of Higuera et al. ^[37] show the increase of turbulence kinetic energy (\( k = \) (\( u^{2} + v^{2} + w^{2} \))/2) in front of and around a vertical wall and a porous breakwater.

(E) Liquefaction: the pressure differential in the soil may produce the liquefaction of the seabed ^[13][38][39], which leads to the loss of the seabed load-bearing capacity. The liquefaction phenomenon happens when the soil effective stresses are cancelled due to an increase of the pore water pressure.

3. Numerical Modelling of Seabed Response

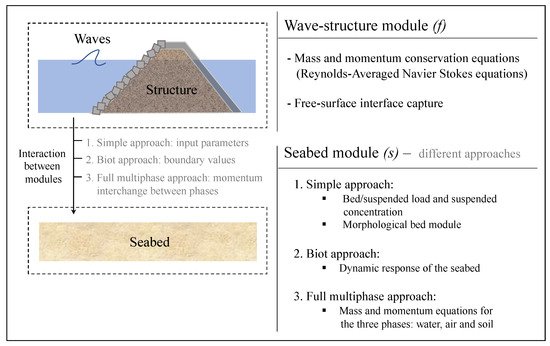
This section presents the governing equations and general methodology of three main Eulerian approaches, in this paper called (i) simple approach, (ii) Biot approach, and (iii) full multiphase approach, for modelling the sediment transport and, thus, the seabed response around maritime structures. The numerical approaches attempt to capture the processes that are involved in the interactions of waves with the structure and their consequences on the seabed foundation. Figure 1 shows a general outline of the numerical approaches described hereafter, which are based on the Reynolds-Averaged Navier–Stokes (RANS) equations (the mass and momentum conservation equations) for the wave–structure interactions and mainly differ in the way that they model the seabed behaviour. This section also shows the applicability and summarizes the performance and parameters used for each numerical methods.

4. Conclusion and Future Prospects

The main objective of this paper is to present a comprehensive review of the numerical approaches for modelling the wave–structure–seabed interactions, while focusing on the seabed response, i.e., scour. This review is intended to complement the review papers on sediment transport and seabed response around maritime structures, which are mainly based on analytical and experimental studies. For this purpose, a literature review of the main and most recent works (over the last 10 years) on numerical modelling was carried out.

In this paper, they are referred to as: (i) simple approach, (ii) Biot approach, and (ii) full multiphase approach. These three approaches are based on Reynolds-Averaged Navier–Stokes equations for the wave–structure module. The simple approach considers: (a) the bed load transport with empirical formulas; (b) the suspended concentration with the advection–diffusion equation and suspended load transport; and, (c) The studies that used Biot’s equations for the seabed module focus more on the stress field and pressures, which is, the mechanical behaviour of the seabed. The full multiphase approach is the more complex approach and is difficult to implement numerically.

The simple approach considers: (a) the bed load transport with empirical formulas; (b) the suspended concentration with the advection–diffusion equation and suspended load transport; and, (c) The wave module is mainly based on RANS or VARANS equations, depending on whether the structure is permeable or impermeable. The studies that use the simple modelling approach mainly focus on small and low weight-structures to simulate the movement and deformation of the seabed (two-coupled approach). For large structures, such as breakwaters, these studies tend to underestimate the scouring results.

The Biot approach involves the RANS or VARANS equations for the wave module and the Biot’s equations for the seabed module. Biot’s equations are used to obtain the seabed displacement and stresses. The outputs of the wave module are used as boundary conditions for the seabed module. The studies that used Biot’s equations for the seabed module focus more on the stress field and pressures, which is, the mechanical behaviour of the seabed.

The full multiphase approach is the more complex approach and is difficult to implement numerically. It solves each phase (sediment, water, and air) with the Navier–Stokes equations (mass and momentum) at the same time and space. Most of the studies are based on small-scale problems given the very high computational costs that are associated with its use.

This entry is adapted from the peer-reviewed paper 10.3390/jmse9060611