Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Food Science & Technology
|
Chemistry, Analytical
The experimental designs for mixtures are a subclass of experimental designs useful for studying the effects of ingredients/components in formulations.
- food formulation
- ingredients
- product development
- DoE
1. Introduction
Mixtures are common matter of everyday life and of many fields of science. Actually, it is quite difficult to think at situations in which mixtures are not concerned. The meaning of “mixture” could be slightly different considering the context as well as different could be the way in which mixtures are prepared. Further, according to the complexity, we can have binary mixtures (made up of two components), ternary mixtures and so on [1,2,3,4,5].
Mixtures are particularly important for the food sector in which, for instance, the formulation of a product consists in the definition of the ingredients and, most important, of their relative proportion in the mixture [6,7]. The concept of “proportions” is a key concept which makes the mixture problem so special [8]. Common situations easily found in the food sector could be the composition of gases for a modified atmosphere packaging [9], a blend of olive oils or wines [10], the composition of a liquid medium for food storage, etc. According to the final aim, food scientists and technicians might be interested in studying and optimizing their mixture for (i) technological applications (e.g., increasing products shelf-life); (ii) nutritional targets (e.g., reaching the required content of fiber to ensure the compliance with health claims); and (iii) organoleptic scopes (e.g., obtaining the desired textural and sensory properties of a baked good).
Considering their widespread diffusion, the study of mixture is of fundamental importance. There are rational approaches that can be used to study the mixtures and they are basically included in the field of the design of experiments (DoE) [8,11]. DoE generally refers to a collection of tools aimed at systematically examining different types of problems in order to obtain the best compromise between information and effort (time, money), i.e., with a relatively small number of experiments [7,12]. DoE is part of the vast area of chemometrics [13].
According to Hibbert (2016)[14], the experimental design is an “efficient procedure for planning combinations of values of factors in experiments so that the data obtained can be analyzed to yield valid and objective conclusions”. To reach such important goal (valid and objective conclusions), there are key steps that could be summarized in the following [11]: (i) define the goal of the experiments; (ii) detect all the factors that can have an effect; (iii) plan the experiments; (iv) perform the experiments; and (v) analyze the data obtained by the experiments.
It should be understood that in this process, the critical step is the planning of the experiments. Once these have been planned in a rational way (which means answering the question: which combinations of the selected factors should I test to gain the maximum information about my system?) they can be performed. Then, regression and analysis of variance (ANOVA) are the tools extensively used to find the relationship between the dependent variables (the response(s) of interest) and the independent variables (the factors) and to evaluate the significance of the factors [12]. More detailed information about the theory and use of DoE can be found elsewhere [8,11,13,15].
2. The Mixture Context
A mixture could be defined in several ways. It could be defined as a “portion of matter consisting of two or more chemical substances called constituents” [16] or, more generally, as a “substance made from a combination of different substances, or any combination of different things” [17]. Further, most important to our scope, by the chemometric point of view, it could be considered a combination of factors (i.e., ingredients) whose total is a constant value, 1% or 100%.
Mixture are represented by the so-called “simplex”, which is the simplest object in the space of a defined dimensionality (n, equal to the number of components of the mixture) having n-1 dimension(s) [7,13]. For example, for a binary mixture, the simplex is a line in one dimension; for ternary mixtures, the simplex is a triangle in two dimensions; for a quaternary mixture, the simplex is a tetrahedron in 3-dimensions. In Figure 1, the simplex for a three components mixture is reported. In the simplex, the vertices correspond to the pure components (i.e., 100% of X1, X2, X3—points A, B and C respectively). The edges of the simplex correspond to all the binary mixtures made up of the components at the vertices of the edge under consideration while the component at the opposite vertex is absent (e.g., point D). Finally, any point inside the simplex represents a ternary mixture (e.g., point E). In Figure 1, the proportion of each component in all the possible binary or ternary mixtures is simply obtained by drawing lines parallel to the edge opposite to the vertex of interest. For example, considering the binary mixture in D, the proportion of X1 can be found on the line parallel to the edge X2–X3 (which is opposite to the vertex X1), which passes through D. In this case, D being a binary mixture between X1 and X2, it is easy to conclude that the relative amount of X1 is 50% (or 0.5).
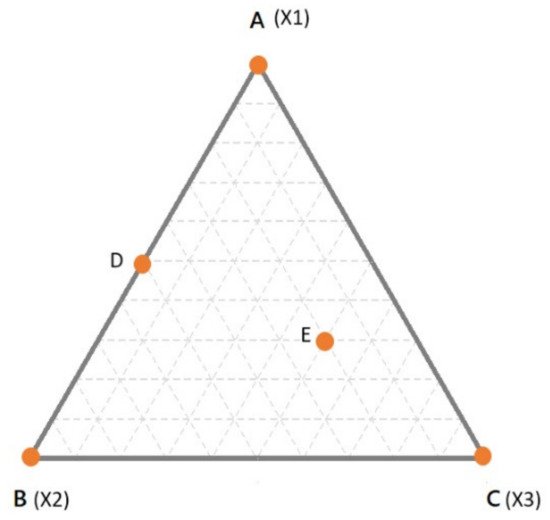
Figure 1. A simplex for a ternary mixture. Dashed lines indicate intervals of 10% of the components.
However, in case of doubts, it may help to simply remind that the vertex represents 100% of that component. Thus, it is obvious that the closer a point is to a specific vertex, the higher is the relative amount. To make it clearer, let us consider the point E. As always, the proportions of the components are found moving in lines parallel to the edge opposite to the corresponding vertex. The line passing through E, which is parallel to X2–X3 edge, tells us the proportion of X1. However, one may be confused if X1 is 0.3 or 0.7. Considering that the line is quite far from the X1 vertex and next to the X2–X3 edge (which is 0% of X1) it is clear that the relative amount should be 0.3. The same goes for the other components and it comes out that the mixture in E is made up of 30% of X1, 20% of X2 and 50% of X3. The sum, of course, is 100%. The interpretation becomes more complicated when the dimensions are higher than 3.
Having in mind the simplex in Figure 1, some peculiarities of the mixture designs (MD) could be highlighted. First of all, it could be easily verified that for each point in the simplex, the implicit constraint (total sum equals to 100%) is fulfilled. Given this implicit dependence, the natural consequence is that the factors of a mixture are no longer independent [11,15]. For independence we intend the possibility to vary the level of a factor independently from the other factor(s) [11,18]. In the mixture context, increasing the amount of X1 will necessarily cause modification in the other component(s). Due to this dependence, the designs employed in other contexts (such as factorial designs), for which the independence of the factors is a fundamental requirement, cannot be applied.
A second important consideration is that mixture designs are thought to study the effect of variation in the proportions of ingredients instead of variation in their absolute values [6,8,11]. In other words, if we are studying the effect of a mixture of N2, CO2 and O2 on the shelf-life of a packaged food or the effect of different flours on dough properties, it does not matter if the package headspace is 10 mL or 100 mL, or the final dough weight is 100 g or 10 kg. What we are looking for is, for instance, the effect of changing the amount of CO2 from 20% to 40% (and obviously reduce the relative amount of the other components).
3. Designs for Mixtures
A mathematical model is associated to each experimental design (not only for mixtures) [7]. Actually, the design is only the tool to calculate the model which is the real information we are looking for. The model should be a priori defined by the investigator according to her/his aims and it defines the postulated relationship between the factors and the response(s). The models for MD are generally presented in the so-called canonical form [8] and the most common ones are the linear, the quadratic and the special cubic.
This entry is adapted from the peer-reviewed paper 10.3390/foods10051128
This entry is offline, you can click here to edit this entry!
