Optimal Configuration of Solar Panel: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Energy & Fuels
Contributor:
Maryon Matius
,
Wan Khairul Muzammil

In solar photovoltaic (PV) energy generation system, the term “photovoltaic” refers to a semiconductor-based device used to convert solar energy (sunlight) into electrical DC energy. To generate electricity, the solar PV generation system has become a mainstream option, especially for the communities who live in rural areas. Its market has vastly expanded in a short period, where according to Parikh, 70% of solar PV module manufacturing is accounted for by China.

  • solar energy
  • solar radiation
  • photovoltaic system
  • insolation
  • isotropic models

1. Introduction

The solar PV system can only be installed in areas where there is enough direct supply of solar energy so that the financial investment becomes worthy [1]. Fortunately, Malaysia is located within the second largest solar radiation region globally, between 1 degree and 7 degrees in north latitude and 100 degrees and 120 degrees in east longitude [2]. Malaysia’s potential for solar power generation is estimated at four times the world fossil fuel resources, since there is an average of 4 to 8 h of sunshine every day [3][4][5]. Authors in [6] remarked that the abundance of solar radiation averaging from 4.8 to 6.1 kWh/m2/day indicates a high potential for solar energy throughout this country. Furthermore, as seen in Figure 1, the photovoltaic power potential in several places in Malaysia exceeded daily totals of 4.0 kWh/kWp [7]. In another study [8], the authors have stated that there is a massive potential of solar energy system resources in electricity generation. Hence, they concluded that the installation of a solar energy system is highly feasible in Malaysia.
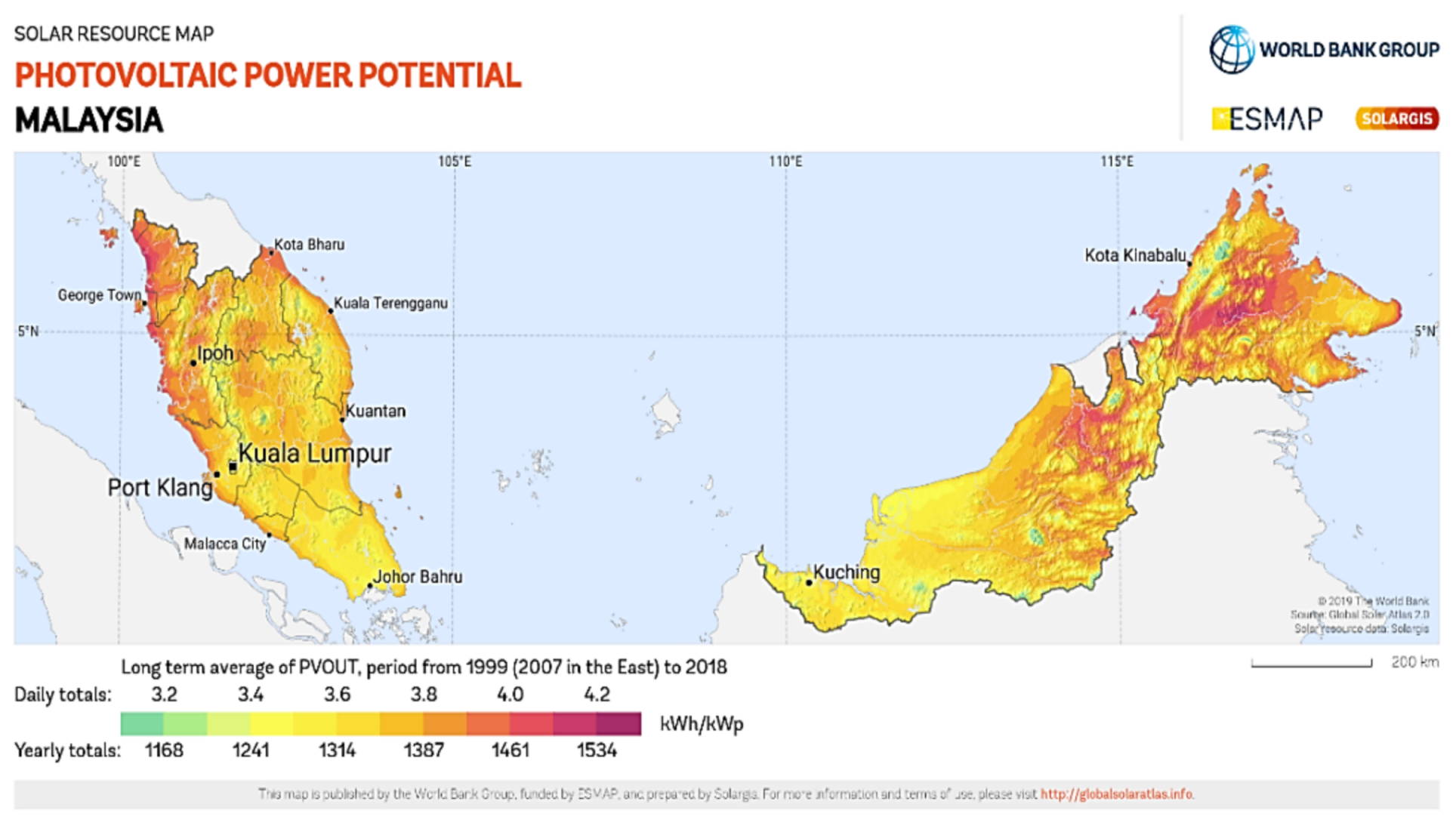Figure 1. Malaysia’s photovoltaic power potential map obtained from the Global Solar Atlas 2.0, a free, web-based application that is developed and operated by the company Solargis s.r.o. on behalf of the World Bank Group, utilising Solargis data, with funding provided by the Energy Sector Management Assistance Program (ESMAP). For additional information: https://globalsolaratlas.info (accessed on 20 November 2020) [9].
On the other hand, a complete working solar PV system is still considered expensive at present [10][11]; however, the average cost of energy (COE) is experiencing a downward trend and is currently cheaper than fossil fuel power plants. Therefore, it is crucial for the maximum amount of sunlight to be captured by the solar PV module. Indirectly, this also helps avoid oversizing the solar PV system and ensuring that it operates efficiently [12]. Hence, to have maximum PV power output, two essential factors, namely, optimum tilt angle and solar PV modules orientation, are crucial for designing and installing solar PV panels. In a study conducted by [13], the authors stated that adjusting the PV module’s tilt angle in different seasons causes more energy to be captured. The sunlight intensity is different according to the season and location, that is, the latitude and longitude, season, local landscape, and local weather [14]. This statement further indicated that the optimum tilt angle and orientation would be different at different times and locations [15]. Hence, this indirectly led to diverse methods being established and developed to determine the maximum solar radiation factors.

2. Solar Models

The method of obtaining the total solar irradiation is done by initially estimating the ratio of diffuse components on a tilted surface to a horizontal surface, which can be classified into two general models known as isotropic and anisotropic models. According to Shukla [16], there are three components of the diffused fraction of radiation on tilted surfaces, comprised of isotropic, circumsolar, and horizon brightening factors. For the isotropic-type models, the intensity of diffuse sky radiation is assumed as uniform over the skydome. Some examples of isotropic models are the Liu and Jordan model, the Koronakis model, the Badescu model, the Tian model, and the Jimenez and Castro model. In comparison, the anisotropic-type model assumes the anisotropy of the diffuse sky radiation in the circumsolar region, as well as the isotropically distributed diffuse component from the rest of the skydome, which is the horizon brightening fraction. Models such as the Temps–Coulson model, Steven and Unsworth model, Hay model, Klucher model, and Gueymard model are examples of anisotropic-type models [16][17][18].
Several past research projects have been conducted to obtain a solar collector’s optimum tilt angle using both the isotropic and anisotropic models and other models. Hailu [17] conducted a study to identify the optimum tilt angle and orientation of a solar module that maximises solar irradiation. The study applied eight empirical models (four isotropic and four anisotropic models) in Canada. As a result, it was found that the anisotropic models were more consistent as compared to isotropic models with varying optimum tilt angles in the range of 46° to 47° and 37° to 44°, respectively. The results also suggest that the collector’s tilt angle should be changed four times over a year to receive more solar radiation. The solar module orientation should be installed with a flatter tilt angle facing west or east due south.
Apart from that, Shukla [16] conducted a study to compare different empirical models’ accuracy by using six empirical models (three isotropic and three anisotropic models) at Bhopal, India. This was done by comparing the empirical models’ results with the ground-measured data from one sample statistical test. The tilt angle was fixed to Bhopal's latitude, 23.26°, and the orientation was also fixed facing due south. The results indicate that among all models, an isotropic model known as the Badescu model possessed minor statistical errors. This model was more suitable for the estimation of solar radiation incident on a tilted surface. Authors in [19] conducted a study to determine the optimum tilt angle and orientation of the PV module by applying the harmony search (HS) meta-heuristic algorithm method in six different places in China. The result has shown that the optimum tilt angle will differ at all the different places; hence, it should be changed once a month, and the PV module is best oriented to face due south. Besides, in a study done by Abdallah [10], a mathematical model was used to estimate the solar radiation on south-facing surfaces with different tilt angles in Palestinian cities. This model has been verified by the Photovoltaic Geographical Information System (PVGIS) and Photovoltaic Software (PVWatts) developed by the NREL. The results show that most Palestinian cities’ annual optimum tilt angle is around 29 degrees, showing a 10% energy gain compared to a solar panel mounted on a horizontal surface.
Meanwhile, Hertzog [20] conducted a study to find the optimum tilt angle of a fixed PV module that was mounted in South Africa by running an experiment. In this study, an experimental design incorporating a two-year longitudinal study was used. The outcome shows that in 2016 and 2017, a PV module with a tilt angle of latitude +10° and a PV module with a tilt angle of latitude −10° yielded the highest output power for winter months and summer months, respectively. However, it is recommended to install the collector at a tilt angle equal to the latitude, as it will cause the highest overall average output power to be yielded. In another study conducted by [21], a mathematical model was used to estimate solar radiation and determine the optimum tilt angle and orientation on a tilted surface. This was done in the high latitudes zone in the Southern Hemisphere, where the method was applied for a specific period and on a daily basis. By positioning the collector monthly at an optimum tilt angle, this achieves a yearly gain in solar radiation up to 1.8 times compared to the case of a horizontal surface.
For research that has been conducted explicitly in Malaysia: authors in [22] conducted a study to optimise the tilt angle of the photovoltaic module installed in five sites, namely, Kuala Lumpur, Ipoh, Alor Setar, Johor Bharu, and Kuching, by using the Liu and Jordan model. The results indicate that for states that are in Peninsular Malaysia, an optimum seasonal tilt is recommended. For states in East Malaysia, a monthly change of tilt angle will help the PV modules capture the maximum amount of solar radiation. Apart from that, the authors in [23] conducted a study to assess the solar radiation on variously oriented surfaces and optimum tilts for a solar collector in Bangi, of latitude 3 degrees north. Seven years’ worth of monthly average daily solar radiation on the horizontal plane was used as an input for the KT solar radiation model and simulated using MATLAB to provide solar irradiation data at various orientations for the whole year. The result shows that the monthly optimum tilt angle changed throughout the year, ranging from −24° (facing due south) to +22° (facing due North). Meanwhile, the annual optimum tilt angle is close to Bangi’s latitude, which is 1.4° facing due south, while the optimum angles for seasonal south- and north-facing surfaces were found to be 14.4° ± 5° and 14.8° ± 5°, respectively. Lastly, a study conducted by [24] intended to evaluate the fixed optimum tilt angle of PV panels at three rural villages, namely Kampung Opar (Sarawak, Malaysia), Kampung Labi (Beaufort, Sabah, Malaysia), and Kampung Orang Asli Kemendol (Selangor, Malaysia). The Liu and Jordan model is applied in this study, and the result has shown that the optimal tilt angle in these three locations is under 5°. A summary of other past research is tabulated in Table 1.
Table 1. Previous research regarding the optimum tilt angle in Malaysia.
Papers Case Study Monthly Optimum Angle Optimum Fixed Tilt Angle Applied Tool Method Orientation of PV
Khatib, Mohamed, Mahmoud, Sopian [22] Kuala Lumpur, Ipoh, Alor Setar, Johor Bharu, and Kuching Provided latitude of the location Excel Liu and Jordan South
Khai, Nor Mariah, Othman, Mohd Zainal [23] Bangi Provided 14.4° ± 5° and 14.8° ± 5°—latitude of the location MATLAB KT solar radiation model Facing south and north
Muhida [25] Kuala Lumpur - 1° to 15° Solar Pro - No difference
Sunderan [26] Ipoh, Perak Provided 0° or tilt angle—latitude of the location - Collares—Pereira and Rabi Facing south and north
Elhassan [27] Kuala Lumpur - 15° to 30° PVSYS-50, Excel, MATLAB - East, north
Daut [28] Perlis Provided - - - -
Khatib [29] Kuala Terengganu Provided 0° to 23° MATLAB Liu and Jordan -
Omidreza [30] Kuala Lumpur - 10° Excel Cooper’s equation -
These previous studies have shown different methods that can demonstrate reliable results. Based on the literature review, the estimation process of the optimal tilt angle and the optimal orientation of solar PV modules are needed as part of the solar PV energy system’s design process. Without an optimal tilt angle and orientation, this will be considered a loss, as the solar PV system’s efficiency is not brought up to the maximum. Furthermore, if this process is skipped, it will cause an over-sizing of the whole complete solar PV system design. Consequently, money will be wasted, and investors will experience losses using this system compared to any other alternatives. Therefore, it will be better to include the design process and obtain the optimum tilt and orientation for a more economical and effective design.

This entry is adapted from the peer-reviewed paper 10.3390/su13105730

References

  1. Burke, M.J.; Stephens, J.C. Political power and renewable energy futures: A critical review. Energy Res. Soc. Sci. 2018, 35, 78–93.
  2. Samsudin, M.S.N.; Rahman, M.M.; Wahid, M.A. Power generation sources in malaysia: Status and prospects for sustainable development. Adv. Rev. Sci. Res. 2016, 25, 18.
  3. Jayaraman, K.; Paramasivan, L.; Kiumarsi, S. Reasons for low penetration on the purchase of photovoltaic (PV) panel system among Malaysian landed property owners. Renew. Sustain. Energy Rev. 2017, 80, 562–571.
  4. Ho, S.; Abraham, L.; Edmund, C.O.; Urrego, L.R. Investigation of solar energy: The case study in Malaysia, Indonesia, Colombia and Nigeria. Int. J. Renew. Energy Res. 2019, 9, 10.
  5. Markos, F.M.; Sentian, J. Potential of solar energy in Kota Kinabalu, Sabah: An estimate using a photovoltaic system model. J. Phys. 2016, 710, 11.
  6. Halabi, L.M.; Mekhilef, S.; Olatomiwa, L.; Hazelton, J. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia. Energy Convers. Manag. 2017, 144, 18.
  7. World Bank Group. Global Solar Atlas Report Kota Belud. 2019. Available online: (accessed on 11 October 2020).
  8. Izadyar, N.; Ong, H.C.; Chong, W.T.; Mojumder, J.C.; Leong, K.Y. Investigation of potential hybrid renewable energy at various rural areas in Malaysia. J. Clean. Prod. 2016, 139, 13.
  9. Global Solar Atlas. Map and Data Downloads. Available online: (accessed on 20 November 2020).
  10. Abdallah, R.; Juaidi, A.; Salameh, A.F.; Agugliaro, F.M. Estimating the optimum tilt angles for south-facing surfaces in Palestine. Energies 2020, 13, 623.
  11. Awasthi, A.; Shukla, A.K.; Murali Manohar, S.R.; Dondariya, C.; Shukla, K.N.; Porwal, D.; Richhariya, G. Review on sun tracking technology in solar PV system. Energy Rep. 2020, 6, 392–405.
  12. Khatib, T.; Muhsen, D.H. Optimal sizing of standalone photovoltaic system using improved performance model and optimisation algorithm. Sustainability 2020, 12, 2233.
  13. Kasirajan, S.; Tan, K.T.; Leong, W.Y. Investigation on tilt angle calculation and irradiation on solar panels. Int. J. Eng. Technol. 2019, 8, 75–78.
  14. Office of Energy Efficiency and Renewable Energy. Solar Radiation Basics. 2020. Available online: (accessed on 5 May 2021).
  15. Li, D.; Lam, T. Determining the optimum tilt angle and orientation for solar energy collection based on measured solar radiance data. Int. J. Photoenergy 2007, 8, 85402.
  16. Shukla, K.N.; Rangnekarb, S.; Sudhakar, K. Comparative study of isotropic and anisotropic sky models to estimate solar radiation incident on tilted surface: A case study for Bhopal, India. Energy Rep. 2015, 1, 96–103.
  17. Hailu, G.; Fung, A.S. Optimum tilt angle and orientation of photovoltaic thermal system for application in greater Toronto area, Canada. Sustainability 2019, 11, 6443.
  18. Kamali, G.A.; Moradi, I.; Khalili, A. Estimating solar radiation on tilted surfaces with various orientations: A study case in Karaj (Iran). Theor. Appl. Climatol. 2006, 84, 235–241.
  19. Mian, G.; Haixiang, Z.; Shengyu, G.; Tingji, C.; Jing, X.; Lexiang, C.; Zhinong, W.; Guoqiang, S. Optimal tilt angle and orientation of photovoltaic modules using HS algorithm in different climates of China. Appl. Sci. 2017, 7, 1028.
  20. Hertzog, P.E.; Swart, A.J. Optimum tilt angles for PV modules in a semi arid region of the Southern hemisphere. Int. J. Eng. Technol. 2018, 7, 290–297.
  21. Soulayman, S.; Mohammad, M.; Salah, N. Solar receivers optimum tilt angle at southern hemisphere. Open Access Lib. J. 2016, 3, 1.
  22. Khatib, T.; Mohamed, A.; Mahmoud, M.; Sopian, K. Optimisation of the tilt angle of solar panels for Malaysia. Energy Sour. 2015, 37, 606–613.
  23. Khai, M.N.; Nor Mariah, A.; Othman, I.; Mohd Zainal Abidin, A.K. Assessment of solar radiation on diversely oriented surfaces and optimum tilts for solar absorbers in Malaysian tropical latitude. Int. J. Energy Environ. Eng. 2014, 5, 1–13.
  24. Fadaeenejad, M.; Mohd Amran, M.R.; Fadaeenejad, M.; Mahdi, Z.; Zohreh, G. Optimisation and comparison analysis for application of PV panels in three villages. Energy Sci. Eng. 2014, 3, 145–152.
  25. Muhida, R.M.A.; Kassim, J.P.S.; Eusuf, M.A.; Sutjipto, A.G.; Afzeri, A. A simulation method to find the optimal design of photovoltaic home system in Malaysia, case study: A building integrated photovoltaic in Putra Jaya. World Acad. Sci. Eng. Technol. 2009, 53, 694–698.
  26. Sunderan, P.; Adibah, M.I.; Singh, B.; Norani, M.M. Optimum tilt angle and orientation of stand-alone photovoltaic electricity generation systems for rural electrification. Appl. Sci. 2011, 11, 1219–1224.
  27. Elhassan, Z.A.M.; Zain, M.F.M.; Sopian, K.; Awadalla, A. Output energy of photovoltaic module directed at optimum slope angle in Kuala Lumpur, Malaysia. Appl. Sci. 2011, 6, 104–109.
  28. Daut, M.I.I.; Irwan, Y.M.; Gomesh, N.; Rosnazri, N.S. Clear sky global solar irradiance on tilt angles of photovoltaic module in Perlis, Northern Malaysia. In Proceedings of the International Conference on Electrical, Control and Computer Engineering, Kuantan, Malaysia, 21–22 June 2011.
  29. Khatib, T.; Mohamed, A.; Sopian, K. Optimisation of a PV/wind micro-grid for rural housing electrification using a hybrid iterative/genetic algorithm: Case study of Kuala Terengganu, Malaysia. Energy Build. 2012, 47, 321–331.
  30. Omidreza, S.K.S.; Elhab, B.; Ruslan, M.H.; Asim, N. Optimal solar panels’ tilt angles and orientations in Kuala Lumpur, Malaysia. In Proceedings of the 1st WSEAS International Conference on Energy and Environment Technologies and Equipment (EEETE’ 12), Zlin, Czech Republic, 20–22 September 2012.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback