Hydrogen bonds (HBs) play a crucial role in many physicochemical and biological processes. Theoretical methods can reliably estimate the intermolecular HB energies. Quantifying an intramolecular hydrogen bond (IHB) strength is not as straightforward as the intermolecular one. The main difficulty lies in isolating the X–H···Y interaction present within a molecule than in a dimer or a complex. However, the procedure discussed (viz. molecular tailoring approach) in this article, allows the generation of fragments so that the atoms/functional groups involved in the HB formation are parts of two different fragments. The energies of these fragments are added or substracted, using the inclusion exclusion principle in set theory, to obtained the energy of HB bond.
- hydrogen bond (HB)
- intramolecular hydrogen bond (IHB)
- molecular tailoring approach (MTA)
- fragmentation methods
- bond energy estimation
1. Introduction
The hydrogen bond (HB) is a dominant noncovalent interaction found in chemical and biological systems [1,2,3,4]. The term “hydrogen bond” seems to have emerged around 1930, from the works of Pauling [1] and Huggins [5,6]. However, the mention of weak, yet specific interactions involving the hydrogen atom is much older. The dimeric association of molecules with hydroxyl groups was suggested by Nernst in 1892 [7]. The term “Nebenvalenz” by Werner [8] and “weak union” by Moore and Winmill [9] are other early stipulations of this noncovalent interaction. In 1920, Latimer and Rodebush [10] suggested that the hydrogen nucleus in an aqueous solution of amines is held jointly by two octets, constituting a weak bond. Barnes, while studying the structure of ice [11], suggested that the hydrogen atoms were midway between the two oxygen atoms, though he did not explicitly mention the hydrogen bond. Huggins [12] claimed that he was the first to propose the term “H-bond” in 1919. His later usage of the term “hydrogen-bridge” may have led to the German word “Wasserstoffbrücke.” The concept of HB gained popularity after Pauling published his classic book, The Nature of the Chemical Bond in 1939 [1]. Pimentel and McClellan [13] suggested that an HB exists when (i) there is evidence of a bond and (ii) there is evidence that this bond involves a hydrogen atom already bonded to another atom. The recent definition of HB by IUPAC [14] is similar in spirit to that in Ref. [13]. The former [14] states that “the hydrogen bond is an attractive interaction between a hydrogen atom from a molecule or a molecular fragment X–H in which X is more electronegative than H, and an atom or a group of atoms in the same or a different molecule, in which there is evidence of bond formation.”
An HB may be generally represented as X–H···Y, where X–H is the proton donor and Y is a proton acceptor. The X–H···Y interactions such as O–H···O, N–H···O, N–H···N, S–H···O, etc., in neutral molecular systems, exhibit interaction energies lying between ~1 to 20 kcal/mol. Typical H···Y distances suggested in the literature fall in the range of ~1.2–3.0 Å and X–H···Y angles lie between 100 and 180° [2,3,4]. The HB’s in liquid water are central to water’s life-providing properties [1,15]. It is stipulated in the literature [16] that if HBs in water were 7% stronger or 29% weaker, water would not be a liquid at room temperature. HBs provide a significant driving force for the native structures and functions of biomolecules [17,18]. Hence, it is of great importance to reliably estimate these X−H···Y HB strengths for shedding light on several physicochemical phenomena and life processes.
The theoretical estimation of intermolecular X–H···Y HB strength in a complex A···B is routinely performed using a supermolecular approach, in which the HB energy (EHB) is estimated as EHB = EA···B − (EA + EB). Several methods for estimating the intermolecular interaction energies are reported in the literature (see, e.g., Refs. [19,20,21,22]). On the other hand, quantifying an intramolecular hydrogen bond (IHB) strength is not as straightforward as the intermolecular one. The main difficulty lies in isolating the X–H···Y interaction present within a molecule than in a dimer or a complex. Many studies for gauging the strength of the IHB in the literature are based on spectroscopic- [23,24,25,26] and electron density topological approaches [27,28,29,30]. Nevertheless, some empirical, semiempirical, and ab initio procedures [31,32,33,34,35,36,37,38,39] have also been reported in the literature for estimating the IHB energy. These have been nicely summarized by Jablonski [40] in his article in this Special Issue, and we shall discuss only the aspects of these methods (e.g., their merits and demerits) that are not explicitly covered in Ref. [40].
One of the early approaches is the conformational analysis (CA), in which two different conformers of the reference molecule are considered. These conformers are chosen such that the HB is kept intact in one of the conformers and is broken in another. The energy difference between these two conformers is then taken as the measure of IHB energy [32,40,41]. A significant disadvantage of this method is that the estimated IHB energy is erroneous due to the incorporation of attractive (syn-anti) or repulsive (anti-anti) additional interaction in one of the conformers [42]. In another similar procedure, viz., the ortho-para method [43], the IHB energy of the X-H···Y bond formed by two substituents, which are ortho to each other, is taken as the energy difference between the ortho and para forms of the reference molecule. However, this method applies only to aromatic systems in which an HB is present in two substituents, which are ortho to each other. The main drawback of this method is that it assumes that the electronic effects caused by the substituent at different positions are similar between the ortho- and para-conformers [44,45,46].
Yet, another indirect approach is the isodesmic/homodesmic reactions. In the former, the IHB making/breaking reaction is written so that the number and type of bonds on either side of the reaction are equal, except the HB, which is retained in one of the reactants [33,47,48]. A further assumption is that the atomic hybridization is conserved on both sides of the reaction. In that case, the method is called homodesmic reaction, which is supposed to give more reliable energy estimates than the isodesmic reaction [49,50,51]. The main drawback of the isodesmic/homodesmic reaction approach is that it does not give HB energy but includes strain energy due to the formation of a ring structure [52]. Another major disadvantage of these indirect methods is that they are applicable only to the evaluation of energy of a single HB present in the system and cannot be employed in a system containing multiple HBs.
Another popular but indirect method is based on the quantum theory of atoms in molecules (QTAIM) [53]. In this method, the presence of a (3, −1) bond critical point (BCP) of the molecular electron density (MED) between H···Y, is considered as the signature of an HB. The large/small value of the MED at the BCP is seen to correlate with strong/weak X–H···Y interaction [54,55,56,57,58]. Espinosa et al. [59] proposed an empirical relation, EHB = 0.5 V(rcp), where V(rcp) is the potential energy density at BCP. Interacting quantum atoms (IQA) [60] framework, leading to QTAIM-compatible energy partition, is another indirect approach wherein the HB energy is calculated as the sum of the classical Coulombic interaction between groups involved in the HB and the exchange-correlation energy. It has been pointed out that there is no check on the reliability of HB energy provided by both of these methods [61,62]. Further, these empirical equations are applicable only when a (3, −1) BCP is present. For instance, a (3, −1) BCP at O–H···O bond is conspicuous by its absence in all the polyols having an O–H···O interactions between the vicinal -OH groups.
2. Intramolecular Hydrogen Bond Energy Estimation by Molecular Tailoring Approach
With the above brief introduction to MTA, we now discuss its application for estimating the IHB energy. As discussed in the introduction section, intermolecular X–H···Y HB energy in a complex A···B is estimated as EHB = EA···B − (EA + EB). This estimation is possible because the energies of the two monomers A and B can be separately calculated. In the case of intramolecular X–H···Y interaction, such a separation is, in general, difficult. However, the MTA procedure allows the generation of fragments so that the atoms/functional groups involved in the HB formation are parts of two different fragments.
The fragmentation procedure is illustrated in Scheme 2 for the test molecule of 1,2,4-butanetriol. In Scheme 2, the parent test molecule, denoted as M, is shown at the center. The geometry of 1,2,4-butanetriol was optimized at the MP2/6-31+G(d,p) (default option: frozen core) level of theory using the Gaussian package [83]. The energy of the optimized structure is −383.01926 a.u. at MP2/6-31+G(d,p) level. The three oxygen atoms are shown as O1, O2, and O3 (see Scheme 2), with the two HB’s, viz., HB1 (O2-H···O1) and HB2 (O3-H···O2) whose energy is to be estimated. For this purpose, the parent molecule is cut into three primary fragments F1, F2, and F3, obtained by replacing −O1H, −O2H, and −O3H groups, respectively, with an H atom each. Dotted circles show these cut regions on the original molecule. The H-atoms are added along the respective C–O bonds (which are cut to form these primary fragments) so that the C–H distance is 1 Å. Hydrogen is the simplest monovalent atom that can be used for satisfying the valencies of cut regions. It is emphasized here that H-atoms placed at slightly different distances (say at 0.9 or 1.1 Å) from the C-atom do not change the results appreciably. This is because of the cancellation of errors in estimating the molecular energy using these fragments. Fragments F4, F5, and F6 are obtained by taking the binary intersection of these primary fragments, i.e., (F1∩F2), (F2∩F3), and (F1∩F3), respectively. Here, intersection means the common structural parts between two primary fragments apart from added H-atoms. For instance, in fragment F4, C1(H2)–C2(H2)–C3(H2)–C4(H2)O3(H) is the common structural part that is also present in fragments F1 and F2. Similarly, fragment F7 is the common intersection of three primary fragments F1, F2, and F3, i.e., (F1∩F2∩F3). A single point energy evaluation, at MP2/6-31+G(d,p) level of theory, is carried out on all seven fragments obtained by the above fragmentation procedure. The fragment geometries are not optimized to avoid the conformational changes in them so that they lead to reliable estimates of IHB energies. It is necessary first to provide a check on MTA application to the parent molecule, M. As discussed above, the actual energy of the original molecule (M) is EM = −383.01926 a.u. at the MP2 level of theory. Using the MP2 single point energies of these fragments, the estimated molecular energy of M is: EM = {EF1 + EF2 + EF3} − {EF4 + EF5 + EF6} + EF7 = {−307.97304 + (−307.9642) + (−307.97765)} − {−232.92410 + (−232.92514) + (−232.93273)} + (−157.88552) = −383.01844 a.u. The error, ΔE = |MTA energy - actual energy| in molecular energy indeed turns out to be very small, viz., 0.00082 a.u. This excellent agreement between the MTA-estimated and actual energy suggests that the present fragmentation scheme is reliable for evaluating HB energies.
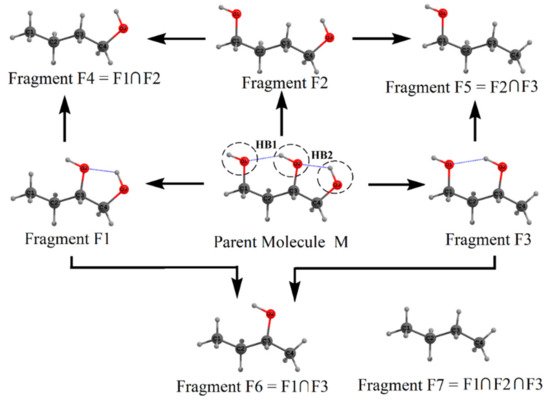
Scheme 2. Fragmentation procedure for estimating the energies of the H-bonds, HB1, and HB2 in 1,2,4-butanetriol (Parent M) molecule. See text for details.
Now we estimate the energy of two hydrogen bonds HB1 and HB2, in the parent 1,2,4-butanetriol. Recall that the hydroxyl groups involved in the formation of hydrogen bond HB1 are O1–H and O2–H. These hydroxyl groups were replaced in fragments F1 and F2, respectively, by H-atoms. Putting the geometry of fragment F1 over F2, we regenerate the parent molecule except following two things: (i) the O–H···O H-bond, i.e., the HB1 interaction between O1–H and O2–H present in the parent molecule is missed out and (ii) there is double counting of common structural part between F1 and F2 (viz., the secondary fragment, F4). Upon addition of single-point energies of fragments F1 and F2, followed by subtraction of the energy of fragment F4 would give the energy of the parent molecule except that the energy of the HB, viz., HB1 is missed out. If the energy of the parent 1,2,4-butanetriol EM is subtracted from (EF1 + EF2 – EF4), the HB energy EHB1 is obtained as EHB1 = (EF1 + EF2 − EF4) − EM = 3.84 kcal/mol. In a similar fashion, EHB2 is obtained as EHB2 = (EF2 + EF3 − EF5) − EM = 1.60 kcal/mol. It should be noted here that these estimated HB energies are in the gas phase. However, the MTA-based method in principle can provide HB energies in the solvent phase, wherein the energies of the fragments in solvent (using continuum solvation model) could be employed.
We note that the two HBs, HB1 and HB2, are interconnected, forming an H-bond network. Such networking of H-bonds leads to a phenomenon called cooperativity [67]. In general, it is anticipated that the strengths of HB1 and HB2 are enhanced because of this networking effect. To estimate the contribution of cooperativity toward each of these two H-bonds, we reestimated the HB energy of these two HBs by isolating them from each other. The difference between the HB energy estimated earlier (in the presence of network) and the one when they are isolated (in the absence of a network) is the cooperativity contribution toward this HB. For example, consider fragment F3 in which only HB1 is present and fragment F1 in which HB2 is present. To estimate the energy of HB1 in the absence of the networking effect of HB2, we consider fragment F3 as our parent molecule. In the present case, fragments F5 and F6 are the two primary fragments that, when placed over each other, would give us the parent fragment F3 except HB1, and fragment F7 is the binary overlap of F5 and F6. Therefore, utilizing these fragments’ energies, the energy of HB1 is obtained as EHB1 = (EF5 + EF6 − EF7) − EF3 = 3.32 kcal/mol. Similarly, the energy of HB2 in the absence of the networking effect of HB1 is obtained as EHB2 = (EF4 + EF6 − EF7) − EF1 = 1.09 kcal/mol. These reestimated HB energies are indeed smaller than those estimated in the presence of the networking effect. The difference in the energy is cooperativity contribution. The cooperativity contribution to HB1 is ![]() = 3.84 − 3.32 = 0.52 kcal/mol and that for HB2 is
= 3.84 − 3.32 = 0.52 kcal/mol and that for HB2 is ![]() = 1.60 − 1.09 = 0.51 kcal/mol. In the present test case, the estimated cooperativity contributions are not large because only two HBs are present. The later sections will show that cooperativity values in some molecules can indeed be as large as a typical HB energy.
= 1.60 − 1.09 = 0.51 kcal/mol. In the present test case, the estimated cooperativity contributions are not large because only two HBs are present. The later sections will show that cooperativity values in some molecules can indeed be as large as a typical HB energy.
The HB energies obtained by applying the above procedure to some alkanetriol molecules are shown in Table 1 [66]. The estimated HB energies fall in a range between 1.50 and 4.97 kcal/mol (see Table 1). This is the expected energy range from chemical intuition. Further, these HB energies are in a qualitative agreement with those expected from the corresponding HB distances. For instance, the strongest HB in 1,2,5-pentanetriol has an energy of 4.97 kcal/mol, with the corresponding HB distance being the shortest (1.80 Å) among all the alkanetriols reported in Table 1. One of the noteworthy results in Table 1 is that the error in estimating molecular energies of all the alkanetriols is quite small, viz., between 0.40 to 0.65 kcal/mol. By considering this accuracy, we estimate the maximum error associated with our calculated HB energies to be 0.3 kcal/mol. The present method is thus capable of calculating accurately the IHB energies and cooperativity values of multiply H-bonded systems.
Table 1. The H-bond (HB) distances (in Å), HB energies (in kcal/mol), and the error in the molecular energy estimation for alkanetriols using similar fragments, ΔE=|EM − Ee|. The corresponding O–H stretching frequencies (cm−1) and the molecular electron density (MED) value at the (3, −1) bond critical point (BCP) (a.u.) are also shown. The calculations are performed at MP2 (full)/6-311++G(2d,2p) level theory.
| Molecule | HB Label |
HB Distances a (in Å) |
HB Energy (kcal/mol) |
ΔE (kcal/mol) |
O–H Stretch Frequency (cm−1) |
MED at (3, −1) BCP (a.u.) |
|---|---|---|---|---|---|---|
| 1,2,3-propanetriol b | HB1 HB2 HB3 |
2.16 2.08 2.58 |
1.90 2.47 1.63 |
0.50 | 3784 3765 3845 |
0.0201 |
| 1,2,3-butanetriol b | HB1 HB2 HB3 |
2.13 2.05 2.58 |
2.13 2.72 1.60 |
0.50 | 3768 3745 3844 |
0.0211 |
| 1,2,4-butanetriol | HB1 HB2 |
1.98 2.22 |
2.90 1.75 |
0.40 | 3789 3828 3875 |
0.0219 |
| 1,2,5-pentanetriol | HB1 HB2 |
1.80 2.25 |
4.97 1.78 |
0.55 | 3669 3825 3865 |
0.0334 |
| 1,3,5-pentanetriol | HB1 HB2 |
1.94 1.96 |
2.91 2.90 |
0.58 | 3763 3792 3875 |
0.0225 0.0239 |
| 2,3,4-pentanetriol b | HB1 HB2 HB3 |
2.12 2.02 2.56 |
2.18 2.94 1.50 |
0.52 | 3759 3731 3820 |
0.0223 |
| 2,4,6-heptanetriol | HB1 HB2 |
1.92 1.93 |
3.02 2.94 |
0.65 | 3753 3773 3857 |
0.0250 0.0242 |
a The MP2 (FC)/6-311++G(2d,2p) optimized geometries were employed. Table 1 is partially reproduced from our earlier study reported in Ref. [66]; Copyright (2006) The American Chemical Society. b The triols wherein three OH groups are present on the successive C-atoms show three H-bonds. See text for details.
This entry is adapted from the peer-reviewed paper 10.3390/molecules26102928
