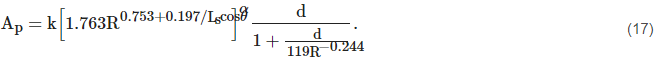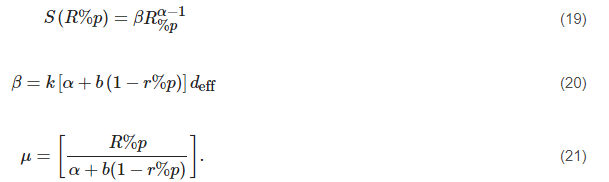Terrestrial Links Rain Attenuation Models

Terrestrial Links Rain Attenuation Models: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Others

Contributor:

Rain is a natural process that attenuates the propagating signal at microwave and millimeter-wave frequencies. Therefore, it is necessary to mitigate rain attenuation to ensure the quality of microwave and millimeter-wave links. To this end, dynamic attenuation mitigation methods are implemented alongside attenuation prediction models that can predict the projected attenuation of the links. Studies on rain attenuation are used in geographically distributed locations to analyze and develop a rain attenuation model applicable over a wide frequency range, particularly radio frequencies over approximately 30 GHz for 5G and beyond network applications.

ITU-R model
rain attenuation
millimeter-wave
rain attenuation time series

1. Preliminaries

1.1. Rain Attenuation Factors

It is crucial to find a justification and insightful analysis to determine the variables that influence rain attenuation. Although rain is a crucial factor influencing rain attenuation, the link distance, frequency, and polarization play a significant role in the determination of rain attenuation. A brief review of more parameters for rain attenuation is presented here. In the literature, various researchers have found different rain attenuation factors for either terrestrial or slant links. In this regard, we compiled 17 parameters that can impact rain attenuation for microwave links using artificial or ML-based techniques ^[1].

1.2. Rainfall Rate Data Collection Procedures

The rain rate is an essential parameter for determining rain attenuation. In this section, different data collection techniques for rain attenuation are discussed.

1.2.1. Available Databases

A newly devised model should check the efficiency for its validity the confirmation. In most cases, the model developer uses the ITU-R DBSG3 rain attenuation database. In some cases, weather databases European Center for Medium-Range Weather Forecasts (ECMWF) or ECMWF re-analysis-15 (ERA-15) were also used as secondary sources of determining the rainfall rate. These secondary databases lack rain attenuation information on terrestrial and earth-space links for tropical regions. Consequently, most of the models developed in tropical countries are needed to create facilities to prepare the rain attenuation databases.

1.2.2. Experimental Setup

A simple method of determining the rain rate is to set up an experiment to deploy measuring equipment such as the use of a disdrometer, weather station, and rain gauges that measure the rain rate at lower integration times (⩽1 min intervals), which can be saved in a personal computer with the help of a dedicated data logger ^[2]^[3]^[4]^[5]. In some cases, the radar information of the rain cell was used to measure the rain rate. The problem with radar-based techniques is that massive investments are required to collect rain rate information if radar systems have not been deployed for other purposes ^[6]^[7].

1.2.3. Rain Rate Data Generation: Synthetic Technique and Logged Data

The rain rate time series in a specific area is essential because it is used to calculate the attenuation in a fixed radio transceiver infrastructure ^[8]. The general procedure for collecting the rain rate time series is to collect the data by employing an experimental setup. Thus, the general approach is time-consuming because a minimum of one year of data should be collected over a particular area. Cost is also associated with this process. In addition to this experimental technique, a synthetic method can be used to calculate the time series using a mathematical approach. Table 1, summarizes the various types of synthetic time series assessment techniques.

1.2.4. Rain Rate Prediction from Spatial Interpolation Techniques

To accurately determine the rain attenuation, it is necessary to consider the spatial distribution of the rainfall intensity. The rain rate cannot be measured everywhere using the rain rate collector, which significantly reduces the accuracy of the experimental setup. However, an intense spatial resolution rain rate is required for accurate estimation. There exist some synthetic techniques by which the undetermined rain rate can be estimated to solve the problem at a particular location.The inverse distance weighting (IDW) technique as per Equation (1) can be used to determine the rainfall rate at ungauged locations ^[9]^[10]:

where N is the number of rain gauges. The rain value $w_{i}$ depends on the location of $d_{i}$ in the estimated position p is given by Equation (1), and $w_{i}$ is given by Equation (2):

The average rainfall rate was then determined from these estimated values, along with the rain gauge readings used in this analysis. Using Equation (1) the rain rate can be predicted up to 10–30 km. Unfortunately, the rainfall data available in the weather database ERA-40 provided by the ECMWF suffer from a low spatial resolution ${1.125}^{\circ} \times {1.125}^{\circ}$ latitude per longitude grid.

The spatial-temporal rainfall distribution mechanisms based on the top-to-bottom data analysis approaches are surveyed in ^[11]. This survey compared most techniques that predict high-resolution space-time rainfall using remote sensing, conventional spatial interpolation, atmospheric re-analysis of rainfall, and multi-source blending techniques, and discussed issues in integrating various merging algorithms. In the article, it was shown that the maximum spatial resolution is available by the Global Satellite Mapping of Precipitation Near Real-Time (GSMaP-NRT) dataset with a resolution of up to $0 . 01^{\circ}$ with an update of once per hour, which is clearly higher than the ECMWF database. Table 2 presents an analysis of different high-resolution spatial rainfall estimation techniques.

Another technique for generating the rain rate is applying the local rain data to the MultiEXCELL model ^[12]. This model was used in ^[13] to generate synthetic rain rates. Transmitting and detecting specific differential phase-shifted signals through a dual-band radar system has been experimented with in ^[14]. As a result of this experiment, the authors noticed the scattering effects in the detected signals that arise due to the radar signals’ differential reflection. A corrector factor should be used for the reflected and differently reflected signals in order to eliminate the scattering effects. The statistical uncertainties of rainfall are then calculated by considering the propagation of the power-law relations.

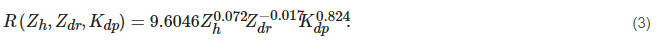
Table 1. Estimation techniques of rain attenuation time series.

Ref.	Estimation Techniques
^[15]	The proposed technique generates rain attenuation time series using storm speeds from 1 to 12 m/s in a two-layered rain structure model. Also, temperature, altitude, and height are used as per the geographic location.
^[16]	$A (t) = \frac{a_{0} \cdot e^{\sqrt{2 d_{A G} / β_{a}} \cdot W (t) + d_{A G} \cdot v_{a} / β_{a} \cdot t}}{1 + d_{A G} \cdot a_{0} \int_{0}^{t} e^{\sqrt{2 d_{A G} / β_{a}} \cdot W (s) + d_{A G} \cdot v_{a} / β_{a} \cdot s} d s}$ where $a_{0}$ :0–0.5 dB, $W (t)$ : Wiener process, $β_{a}$ , $v_{a}$ : gamma distribution parameters, $d_{A G}$ : Dynamic parameter $β$ of the Maseng-Bakken model.
^[17]	It proposed an enhanced technique to generate rain attenuation time series where precise rain rates are not available at global scale using ITU-R model. The technique uses mean and standard deviation of rain rate either from NOAA ^[18] and ITU-R model ^[19] and the output of Gaussian noise through a low-pass filter (LPF: $k / p + β$ , cut-off frequency f_c: 0.2 MHz) into a non-linear memoryless device, where $A_{offset}$ is the calibration factor, $A_{offset} : e x p (m + σ Q^{- 1} (P_{0} / 100))$ and Q: zero-mean, unit variance Gaussian probability density function.
^[20]	$A (x_{0}) = k_{A} \int_{0}^{L_{A}} R^{α_{A}} (x_{0} + Δ x_{0}, ξ) d ξ + k_{B} \int_{L_{A}}^{L_{B}} R^{α_{B}} (x_{0}, ξ) d ξ$ where $L_{A}$ and $L_{B}$ are the radio path lengths, $Δ x_{0}$ is the shift due to the presence of layer B, $x_{0} = v \cdot t$ , and v is the average storm speed (typically 10 m/s).
^[21]	$A (t_{0}) = \frac{1}{cos θ} [\int_{d_{0}}^{d_{0} + S_{A}} k_{A} R {(l)}^{α_{A}} d l + \int_{d_{0} + S_{A}}^{d_{0} + S_{A} + S_{B}} k_{B} 3 . 134^{α_{B}} R {(l)}^{α_{B}} d l]$ , where $θ$ :link elevation angle, ( $α_{A}$ , $k_{A}$ ), ( $α_{B}$ , $k_{B}$ ): power-law coefficients that converts the rain rate into specific attenuation for layers A and B, respectively, and R: rain rate along the link.
^[22]	A copula is a multivariate distribution function expressed by marginally uniform random unit interval variables and it can avoid dependence index like in log-normal distribution. The procedure is: $ρ = sin (\frac{π τ}{2}) \to$ zero mean Gaussian random variables correlated matrix→normal CDF→desired random variable→inverse CDF of the desired distribution.
^[23]	The procedure is: $R_{G} = e^{- β \cdot \| τ \|} \to [β_{E M B}, β_{g a m m a}] \to H (z) = \frac{\sqrt{1 - e^{- 2 β T_{s}}}}{1 - z^{- 1} e^{- β T_{s}}}$ , where $T_{s}$ : sampling time, and $β_{E M B}$ and $β_{g a m m a}$ are $12.3 d^{- 0.95} \times 10^{- 4}$ and $6.9 d^{- 0.6} \times 10^{- 4}$ , respectively.
^[24]	The procedure is: $a_{k} = \frac{1}{N} \sum_{j = 0}^{N - 1} M_{j} e^{- \frac{i 2 π}{N} k j} = ℑ (M_{j}) \to a_{k} = \sqrt{h_{k} ℑ (c_{G})} \times e_{k} \to M_{j} = ℑ^{- 1} (a_{k}), [h_{k} = 0.5]$ , where $M (t)$ : Gaussian process, ℑ and $ℑ^{- 1}$ are direct and inverse Fourier transforms, respectively.
^[25]	Compute the stochastic differential equation: $d A (t) = \frac{μ}{4} d_{a} (\frac{μ^{2}}{λ} A (t) - A^{2} (t) + μ^{2}) . d t + \sqrt{d_{a} \frac{μ^{3}}{λ}} A (t) d W (t)$ , where $d_{a} = 2 β_{a} S_{a}^{2} \frac{λ}{μ^{3}}$ , where $μ$ and $γ$ are found by fitting to experimental first order statistics of rain attenuation, $β_{a}$ and $S_{a}$ are the parameters of the diffusion coefficient of the M-B model.
^[26]	Compute: $P (t_{i}) = 1 - P_{0, i} \to z_{i} = T_{z} (r_{i}) \to find M_{z} (d) \to Gaussian PDF \to ρ_{j} (τ) \to H_{i} (z)$ , where $P_{0, i}$ is the possibility of rain in the ith station, $r_{i}$ represents a nonlinear transformation $T_{z}$ , and $ρ_{j}$ is the temporal autocorrelation function of rain attenuation for ith link.

Table 2. Highly spatial resolution rainfall estimation models.

Ref.	Technique or Resolution
^[3]	Analyzed millimeter-wave and showed that the ITU-R predicted rainfall rate of region P is up to 0.01% of time (agrees → 99.99% of time and disagrees → 0.01% of time).
^[11]	This multi-source blending technique to estimate high-resolution space-time rainfall scales to develop and merge remote sensing, conventional spatial interpolation, atmospheric re-analysis of rainfall, and multi-source blending techniques.
^[27]	It presented gauged-based data re-analysis at a resolution of $0.5^{\circ} \times 0.5^{\circ}$ .
^[28]	In GSMaP-NRT, it analyzed the satellite, microwave-infrared, and near real time weather dataset to compare better predictability presented resolution about $0.01^{\circ} \times 0.01^{\circ}$ .
^[29]	ECMWF: $1.125^{\circ} \times 1.125^{\circ}$
^[30]	It proposed the spatial and the temporal correlation functions to determine rainfall rate.

Table 3. Techniques to calculate effective path length (EPL) or path length coefficient factor (PCF).

Ref.	EPL or PCF	Parameter Settings	Remarks
^[2]	$r = 1 / \{1 + 0.03 {(100 P)}^{β l^{m}}\}$ $^{⧫}$	Method: Practical measurement; Frequency band: 7–38 GHz; Path length: 58 km; and rain rates were collected over 1-min time interval.	The correction factor depends on $β$ ; link length; and $p %$ of rain
^[31]	$r_{r a d} (t) = {A_{r a d,}}_{d} (t) / γ_{R} d$	Method: Simulation Frequency: 22 and 38 GHz Path lengths: 2, 5, 10 and 20 km	The correction factor only depends on the $A r a d, d (t)$ , and $γ R (t)$ .
^[32]	$r = \frac{1}{1 + \frac{L}{\frac{2636}{R (P) - 6.2}}}$	Method: Practical measurement Rain rate: 5-min point at 11 GHz frequency; 42.5 km long radio link with $R > 10 mm / h$	The correction factor depends on the radio link length and rain rate.
^[33]	$r = 1.08 L^{- 0.5108}$ (7 GHz for 0.01% of the time)	Method: Practical virtual link; Link length: 1–10 km; Time exceedance: 0.01%; Frequency 7 GHz	The reduction function depends only on the total path length. Estimation: Exponential curve fitting
^[34]	$d_{e f f} = \frac{1}{1 + d / d_{0}} \cdot d$	Method: Practical setup; Site: S. Paulo, Brazil; Season: Dry season; Frequency: 15 GHz (4 links) and 18 GHz (2 links) with vertical and horizontal polarizations; Path lengths: 7.5–43 km; Duration: 1–2 year	The correction factor depends only on the rain rate exceedance of $p %$ of the time. Estimation: exponential curve fitting
^[35]	$r (R_{0.01}, L) = L \times (\frac{- R_{0.01}}{1 + ζ (L) \times R_{0.01}})$ $^{▴}$	ITU-R database; Site: 8 countries; Path lengths: 1.3–58 km; Frequency: 11.5–39 GHz; Rain rates (0.1%): 18–105mm/h	The PCF depends on rain rate exceedance $% p$ of time and link length. Estimation: curve fitting
^[36]	$r = 3.6435 {R_{p}}^{- 0.377}$	Method: Practical setup; Link length: 2.29 km; Rain Gauge: Tipping rain bucket (0.254 mm accuracy); Frequency: 28.75 GHz	The correction factor depends only on the rain rate exceedance of the $% p$ of the time. Estimation: curve fitting.
^[37]	$r (R_{0.01}, d) = d / [1 + \{d / 2.6379 {R_{0.01}}^{0.21}\}]$	Practical setup; Link length: unavailable; Rain Gauge: Tipping, Frequency: 15 GHz, Availability: 99.95%; Duration: 4 years; Rain rate: R (0.1 to 0.001)	The correction factor depends only on the rain rate exceedance of the $% p$ of the time and LOS link length. Estimation: exponential curve fitting
^[38]	$r = 1.303 \frac{ς}{1 + \frac{L}{D}}$ $^{♣}$	Model: empirical model, based on the point of inflexion (POI)	The correction factor depends only on the slant path length and the rain cell diameter.
^[39]	$r = A / (k R_{T X}^{α} L_{s l a n t})$	Method: MultiEXCELL rain simulation. Calculation: rain attenuation is calculated via the numerical approach. Rain field size: 1 km × 1 km to 250 km × 250 km	The correction factor depends on calculated attenuation, specific attenuation conversion coefficients, ‘measured’ rain rate at the transmitter end, and the LOS link length.
^[40]	$r = \frac{1}{[0.477 L^{0.633} R_{0.01 %}^{0.073 α} f^{0.123} - 10.579 (1 - e^{- 0.024 L})]}$	(1) Can be used worldwide; (2) frequency band: 5–100 GHz; (3) Maximum path length is 60 km	The correction factor depends on the frequency (GHz), specific attenuation coefficient ( $α$ ), and link length (L).
^[41]	$r = \{\begin{matrix} \frac{N_{e}}{cos θ} (\frac{h_{R} - h_{S}}{tan θ}) & R < R_{0} \\ \frac{N_{e}}{cos θ} (\frac{1}{0.056 + 0.012 R}) & R \geq R_{0} \end{matrix}$	The number of effective cells $(N_{e})$ is calculated after analyzing ITU-R DBSG3 database.	To define the rain cell, it needs to know the cell $(R_{0})$ boundary rain rate.
^[42]	$r = \{\begin{matrix} [\frac{1}{1.77 d^{0.77} R_{0.01}^{- 0.05}}] & f \leq 40 GHz \\ {[\frac{1}{0.477 d^{0.633} R_{0.01}^{0.073} f^{0.123}}]}^{2} & f > 40 GHz \end{matrix}$	It was based on the measured attenuation of smaller than 1 km terrestrial link and frequency 26/38 GHz.	It concluded that the distance factor is inconsistent for a link length smaller than 1 km.

$⧫ m (F, l) = 1 + Ψ (F) \ln l$ and $Ψ (F) = 1.4 \times 10^{- 4} F^{1.76}$ the value of depends on path length and the considered rain percentage exceedance, $^{▴} ζ (L) = - 100$ when $L \leq 7 km$ and $ζ (L) = {⌈ (\frac{44.2}{L}) ⌉}^{0.78}$ when $L > 7 km$ , $^{♣} ζ_{0.01} = ζ_{1}$ ; $R_{0.01} \geq 110$ mm/h, otherwise $ζ_{0.01} = S_{2}$ or $ζ_{2} S_{3}$

Table 4. Error estimation techniques for rain rate prediction

Ref.	Technique or Resolution	Remarks
^[43]	$E = \frac{1}{n C o u n t r y} \sum_{i = 1}^{415} W_{i} \|log (\frac{{R_{i}}^{D B S G 3}}{{R_{i}}^{S - B}})\|$	This test was used to re-analysis based rain rate and the rain rate provided by the ITU-R DBSG3 database.
^[44]	$E_{R 0.01} = \sqrt{E_{ψ}^{2} + E_{ϕ}^{2} + {Δ R_{0.01}}^{2}}$ where $E_{ψ}^{2} = {(\frac{\partial R_{0.01}}{\partial ψ})}^{2} σ_{ψ}^{2}$ and $E_{ϕ}^{2} = {(\frac{\partial R_{0.01}}{\partial ϕ})}^{2} σ_{ϕ}^{2}$ .	The model was developed and verified using DBGS3 along with CHIRPS rainfall ( $ψ$ ), and TPW ( $ϕ$ ) in the ERA-Interim Reanalysis database. Authors have not compared with measured data and the precise calculation of rain rate $R_{0.01}$ showed lower accuracy (uncertainty is about 14%).

The wet-antenna effect has relation with the bias value of the signal in the receiver section. However, an appropriate bias compensation technique has not yet been developed.

A rain-rate-retrieval algorithm was designed using radar reflectivity derived from the rain rate in ^[45]. Based on the Doppler velocity, the derived radar reflectivity was classified as low-and high-rain cases. This model paved the way for blending reflectivity and attenuation to predict the rain rate. However, beyond reflectivity and attenuation, other factors, such as seasonal variation and rain type, were not considered.

The minimum observed attenuation and the maximum observed attenuation were calculated through a commercial microwave link (CML) within a fixed interval ^[46]. Using these minima and maxima, the observed attenuation value averaged rain-intensity can be calculated as

where B (in dB) is the induced bias value because of to the mixture of the transformation of the min/max with the quantizer, the negative values of (

A_{i}^{r_max} - B

) are counted as zeroes when they exist,

\tilde{a} = a \cdot {[ln (K) + 0.57722]}^{b}

, and the a and b parameters refer to the power-law relationship of specific coefficients and K is the number of instantaneous samples per interval from which the maximum attenuation is extracted.

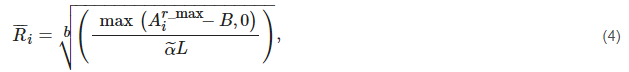
Since 2000, numerical weather prediction (NWP) has become popular in predicting rainfall and has drawn interest from the meteorological forecasting industries, researchers, and other stakeholders. However, owing to decreased portability and implementation coverage in remote locations, NWP-based techniques are not a potential technique for remote area application. Therefore, the prediction of learning supported rain diminution is standard because the problem of the NWP technique can be solved. In ^[47]^[48]^[49]^[50]^[51]^[52]^[53] ML-based rainfall prediction techniques were presented. Table 4 lists some of the error estimation techniques for rain rate prediction.

1.3. Distance Correction

The rain attenuation (A) was calculated by multiplying the specific attenuation and the distance between the transmitting and receiving antennas.

Assuming the effective path length $L_{e}$ to be 1 km, in Equation (5) the specific attenuation and the link attenuation are equal. Equation (5) is true if the rain and cloud are uniformly distributed over the entire path between the transmitting and receiving antennas. However, if the distance between the transmitting and receiving antennas is not 1 km:

Owing to the non-uniform distribution of rain, the values of the specific and link attenuation (for 1 km length) are different, which defines a term called the effective path length. This implies that the effectual and actual distance varies for non-uniform rain distributions and links. The effectual distance is usually calculated based on the rainfall distribution ^[2]. Many models calculate the effective path length using a correction factor, referred to as the path adjustment factor. In terrestrial links, all the link lengths remain within a single rain cell for a short link or many cells for a long link. A brief discussion on the parameters that affect either the effective path length or path length adjustment factor is presented in the next section. In most cases, the accuracy of the model discussed above was calculated using the measured rain attenuation data, which was then compared to the attenuation derived through the attenuation formula. In some cases, the root means square (RMS) and standard deviation (STD) values were calculated to validate the model. Table 3 contains all of the most critical effective path length or distance correction factors proposed in the literature.

1.4. Frequency and Polarization

The specific attenuation can be determined from the rainfall rate, frequency and polarization using the following power-law relation^[19]^[54]^[55] .

where $R_{0.01}$ is the rain rate, and x and y are regression coefficients that depend on several factors such as: polarization, carrier frequency, temperature, and rain drop size distribution^[54] . The values of x and y can be determined experimentally as empirical values. ITU-R P. 838-3^[19], provides the prediction values for x and y for 1–100 GHz frequency bands at horizontal and vertical polarizations.In this section, various parameters of rain attenuation, rain rate data collection procedure, available public domain databases, time-series generation techniques, percentage of time exceedance of rain (Equation (7)), specific attenuation coefficient determination procedure, and the procedure of distance correction factor have been discussed. All the data collected or modified through these techniques can be used by the rain attenuation models, which will be discussed in the next section.

2. Rain Attenuation Models: Terrestrial Links

Existing terrestrial models can be classified into five categories based on the formulation of the rain attenuation model. These include the empirical, physical, statistical, fade slope, and optimization-based models.

Empiricalmodel: The model is based on experimental data observations rather than input-output relationships that can be mathematically described. The model is then classified as an empirical category.
Physical model: The physical model is based on some of the similarities between the rain attenuation model’s formulation and the physical structure of rain events.
Statistical model: This approach is based on statistical weather and infrastructural data analysis, and the final model is built as a result of regression analysis in most cases.
Fade slope model: In the fade slope model, the slope of attenuation from the rain attenuation versus time data was developed with a particular experimental setup. Later, these data were used to predict rain attenuation.
Optimization-based model: In this type of model, the input parameters of some of the other factors that affect the rain attenuation are developed through optimization (e.g., minimum error value) process.

Figure 1, represents a taxonomy of the well-known and recently developed rain attenuation models used in this study.

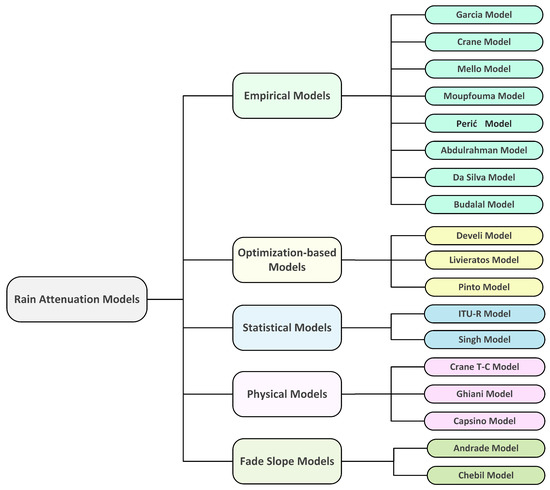
Figure 1. Taxonomy of terrestrial rain attenuation models.

2.1. Empirical Models

2.1.1. Moupfouma Model

This model ^[35] uses the rain rate exceeded by 0.01 percent of the time and the calculation of the proportion of time-correlated with the excess of any given interest attenuation.

where $L_{e q}$ is the equivalent path length for which the rain propagation is assumed to be uniform.

2.1.2. Budalal Model

In this model ^[42] according to the 300 m link’s attenuation analysis with frequencies of 26 and 38 GHz, the authors found attenuation inconsistency provided by the latest ITU-R model. They then investigate the specific attenuation ( $γ_{t h}$ ) as per ITU-R P.838-3 ^[19] and found an inconsistency between the effective specific attenuation ( $γ_{e f f}$ ) can be defined as Equations (10) and (11):

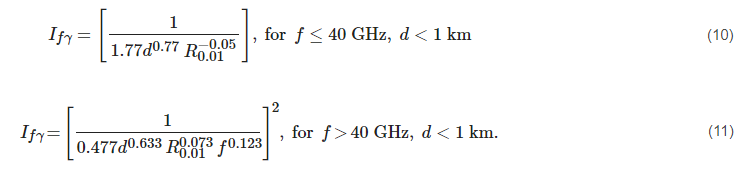
It is inferred that the model can be used for short-range outdoor links with frequencies higher than 25 GHz in 5G networks.

2.1.3. Perić Model

This model is also referred to as a dynamic model ^[56]. It depends on the cumulative distribution function of the rain intensity of the area of interest, the number of rain events in which the rain intensity threshold is exceeded, the rain advection vector intensity, and the rain advection vector azimuth. The model considers the spatial distribution within a 10 km radius around an antenna and is suitable for small geographical areas, up to 10 km × 10 km. Furthermore, it has not been tested in a real-world network environment.

2.1.4. Garcia Model

It is one of the modified version ^[57] of Lin model ^[32], assuming that the path length reduction coefficient changes with the path length and rainfall rate. The developed model was tested with in Paris, Stockholm, Dijon (France), and Kjeller (Norway), with variations in frequency and path length. The model is best suited for temperate European regions.

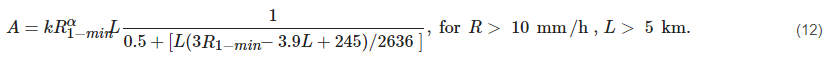
This model improves the limitation of the 5-min rain rate requirement of the original Lin’s model. This model’s drawback is that it was only tested at 11 GHz and not at higher frequencies. Furthermore, the model did not consider spatial rain distribution variations. Another limitation of this model is that it only applies to terrestrial links.

2.1.5. Da Silva/Unified Model

This model ^[58] uses the full rainfall rate distribution with multiple nonlinear regressions from the rain attenuation database. It is primarily developed for terrestrial links and can be later extended to slant links. For a terrestrial link,

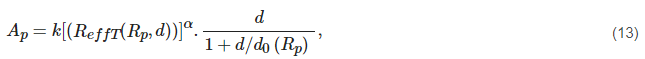
where $R_{e f f T}$ is the approximate effective rain rate for terrestrial links and the and the cell diameter $d_{0}$ is given by Equations (14) and (15) respectively.

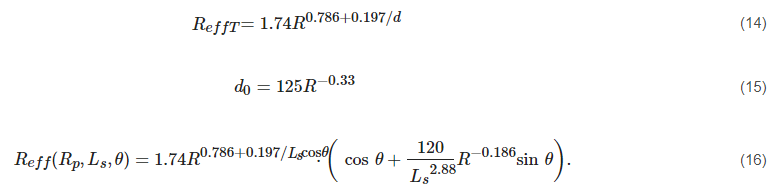
For the terrestrial case $L_{s} = d$ , the second term in the brackets vanishes as $θ = 0^{\circ}$ , and the expression is reduced to the terrestrial case prediction method. With the correct consistency for terrestrial and slant paths, the model exhibits good performance; however, the error has not been compared with real attenuation data.

2.1.6. Mello Model

According to this model^[59] the cumulative probability distribution of rain attenuation for terrestrial link can be determined by the Equation (17):

2.1.7. Abdulrahman Model

According to this model^[60]

the rain attenuation is given by the Equation (18):

where

2.1.8. Crane Model

This model ^[61] establishes rain distribution from a global perspective and the USA’s precise rain distribution maps. From these maps, the rain rate distribution can be calculated.

If the path length $D > 22.5 km$ , then the rain rate should be modified:

where $D_{0} = 22.5 km$

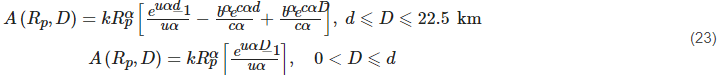
where the constants are given by Equation (24)

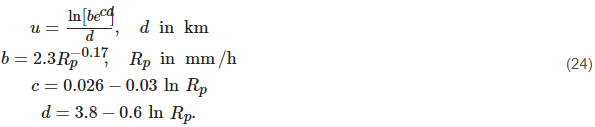
2.2. Physical Models

2.2.1. Crane Two-Component (T-C) Model

This model ^[62] is based on different integration techniques for heavy and light rainfall regions. The author proposed two versions of the T-C models: the first is a simple T-C model and was published in 1982. The model consisted of several steps. (1) Determining the propagation path for the global climate. (2) Finding a mathematical relation between the projected path length in the rain cell and debris region. (3) Fixing the expected amount of attenuation. (4) Deriving the required rain rate to produce rain attenuation and calculating the probability that the specified attenuation is fixed in step (3).

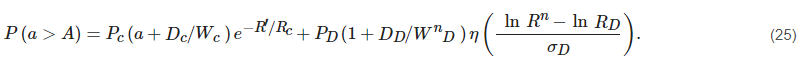
The model was primarily developed for Western Europe and the USA, and has difficulty in determining rainfall parameters, such as the probabilities of occurrence and mean rainfall, for weak and strong rain cells. Sometimes these weak and strong rain cells are referred to as debris and cell, respectively. The model was verified for both the satellite and terrestrial links.

2.2.2. Ghiani Model

This model ^[63] is based on a PCF-correction-based model for terrestrial links. It can be modeled by simulation with Equation (26) and analyzed with Equation (27):

(1) Calculate

(2) Calculating the PCF: $P C F = A / k {R_{T X}}^{α} L$ for the number of rain maps generated by the MultiEXCELL model. This results in the following expression:

where the symbols a, b, and c are taken from the regression coefficients. These three coefficients depend on the values of frequency and path length.

(3) Because the effect of the frequency is negligible

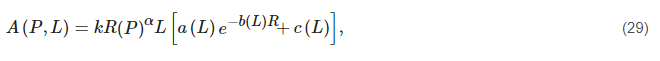
where the constants are given by the set of equations in (30),

This model’s drawback is that the RMS of the prediction error against the ITU-R database did not exhibit better performance compared to the ITU-R and Brazilian models. Thus, a better terrestrial link rain database from DBSG3 or Comité Consultatif International des Radiocommunications (CCIR) was required for examination before its final application.

2.2.3. Excell/Capsoni Model

The parameters of this statistical model ^[64] of the horizontal rain structure can be determined based on the local statistical distribution of the point rainfall intensity. The model was validated using the COST 205, 1985 database. This model consists of several rain cell structures, collectively refereed to as kernels. In such a rain cell, the rainfall rate at a distance l from the center is given by:

Probability of attenuation equation:

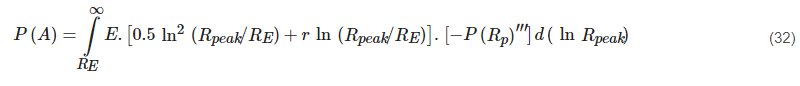
where $r = 1 / 4 π {\bar{l}}_{0}$ .

Rain distribution can be calculated as:

Here, $P (R) = 0$ indicates that the probability of rain is zero, which will be true at the rain cell boundary. A simplified version of the model with the point rain intensity at point (x,y) can be defined as:

along a cell radius:

In the sense of the rain attenuation model, this model does not provide attenuation. However, it facilitates the generation of a synthetic rain rate from which attenuation can be predicted using a suitable prediction model. There are critics that the exponential rain peak is not present ^[65] in nature, and the model does not differentiate between stratiform and convective rain.

2.3. Statistical Models

2.3.1. ITU-R Model

This model ^[40] is primarily based on a distance factor that relies on the rain rate $R_{0.01}$ , frequency, link length, and power-law relationship coefficients of the specific attenuation $α$ (furthermore, it is a function of frequency and polarization). The attenuation and the distance factors can be calculated as:

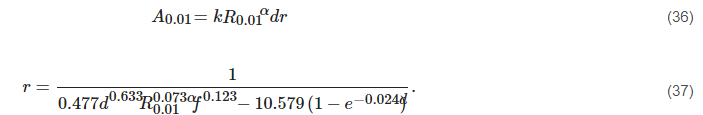
The attenuation, $A_{p}$ , which exceeded for a percentage of time p other than 0.01%, was determined by the simplification of the attenuation $A_{0.01}$ . This model, validated in Malaysia, showed good agreement with the measured attenuation ^[66].

2.3.2. Singh Model

This model ^[67] provides an easy calculation mechanism compared to the ITU-R model. The specific attenuation follows the ITU-R model for the frequency band of 1–100 GHz. After calculating the specific attenuation, the curve fitting technique using the MATLAB software cubic polynomial Equation (38) is approximated for the specific attenuation.

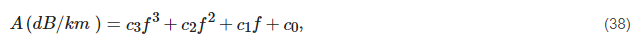
where the coefficients $c_{3}$ , $c_{2}$ , $c_{1}$ , $c_{0}$ of Equation (38) for the horizontal polarization are given by:

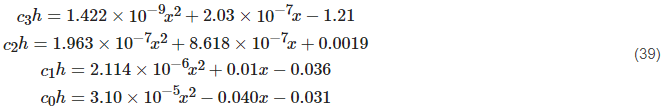
and for the vertical polarization:

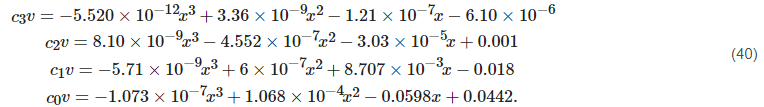
A similar approach-based technique was proposed in^[68] . However, it was considered the original power-law relationship rather than the simplified polynomial form in that proposal. The second difference is that the constants k, $α$ referring to the Equation (42) depends only on frequency and either vertical or horizontal polarization.

2.4. Fade Slope Models

2.4.1. Andrade Model

In the Andrade model ^[69] the variance of the fade slope is proportional to the attenuation as per Equation (43):

The predictor can estimate the next attenuation level $A (t_{i} + t_{p})$ from the current attenuation value $A (t_{i})$ and fade slope:

where $t_{p}$ is the prediction time, it can be considered that $t_{p} = 10$ , which corresponds to the minimum prediction time, that is, the sampling time of the experimental data.

2.4.2. Chebil Model

In the Chebil model^[5] the variance of the fade slope is proportional to the attenuation as per Equation (45):

where the $σ_{ξ}$ is given by Equation (46)

2.5. Optimization-Based Models

2.5.1. Develi Model

This model ^[70] is based on the Differential evolution approach (DEA) optimization technique and experimentally tested at 97 GHz on terrestrial link in the United Kingdom (UK). The steps of the DEA attenuation model are as follows:

(1) The rate of rainfall and percentage of the time exceedance is related to the rain attenuation by equation:

where $a_{k}, b_{n}$ ( $k = 0, 1, \dots, K$ , $n = 1, 2, \dots, N$ ) are the model parameters. $K + N$ is the total number of input variables in the model.

(2) The mean absolute error is:

which can be alternatively represented as:

The mean absolute error given by this equation is treated as the cost function and used to obtain the optimized error by applying the DEA algorithm.

(3) Mutation:

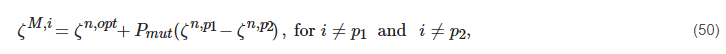
where n is the generation index, $P m u t$ is the mutation variable, $p_{1}, p_{2}$ and i are three arbitrarily chosen individual indexes, and the M and $o p t$ refer to the gene pool and the optimal entity in the population, respectively.

2.5.2. Livieratos Model

This model ^[71] was developed using a DBSG3 database-based on a supervised machine-learning (SML) technique. In this rain attenuation model, the SML technique was blended with a Gaussian process (GP). A rain attenuation algorithm must be trained in a particular area of interest to measure the different interdependencies of the parameters for detecting rain attenuation in a specific region, weather, or carrier frequency.

2.5.3. Pinto Model

This model ^[72] is based on the actual distance correction mechanism through the distance correction factor (r) along with the effective rainfall rate distribution ( $R_{eff}$ ). It uses the quasi-Newton method in addition to particle swarm optimization (PSO); minimizing the root mean square error (RMSE) is the objective function in both cases.

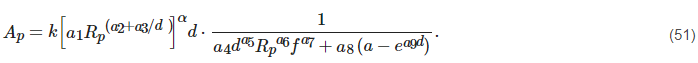
The $a_{i} (i = 1, 2, \dots, 9)$ coefficients can be calculated using quasi-Newton multiple nonlinear regression (QNMRN) and the Gaussian RMSE (GRMSE) algorithm. These coefficients were further fine-tuned using the PSO technique. The model performance has not been compared with the recently developed model, except for ITU-R P.530-17 ^[40]. Thus, there is a need for further verification before application, except for the temperate climate and Malaysia rainfall database areas.

This entry is adapted from the peer-reviewed paper 10.3390/s21041207

References

Samad, M.A.; Choi, D.Y. Learning-Assisted Rain Attenuation Prediction Models. Appl. Sci. 2020, 10, 6017.
Shayea, I.; Rahman, T.A.; Azmi, M.H.; Islam, M.R. Real measurement study for rain rate and rain attenuation conducted over 26 GHz microwave 5G link system in Malaysia. IEEE Access 2018, 6, 19044–19064.
Al-Saman, A.M.; Cheffena, M.; Mohamed, M.; Azmi, M.H.; Ai, Y. Statistical Analysis of Rain at Millimeter Waves in Tropical Area. IEEE Access 2020, 8, 51044–51061.
Choi, D.Y. A study on the rain attenuation prediction model for ubiquitous computing environments in korea. In Proceedings of the International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Bournemouth, UK, 9–11 October 2006; Springer: Bournemouth, UK; pp. 1242–1249.
Chebil, J.; Islam, M.R.; Zyoud, A.H.; Habaebi, M.H.; Dao, H. Rain fade slope model for terrestrial microwave links. Int. J. Microw. Wirel. Technol. 2020, 12, 372–379.
Capsoni, C.; Fedi, F.; Magistroni, C.; Paraboni, A.; Pawlina, A. Data and theory for a new model of the horizontal structure of rain cells for propagation applications. Radio Sci. 1987, 22, 395–404.
Leitao, M.J.; Watson, P.A. Method for prediction of attenuation on earth-space links based on radar measurements of the physical structure of rainfall. IEE Proc. F Commun. Radar Signal Process. 1986, 133, 429–440.
Diba, F.D.; Afullo, T.J.; Alonge, A.A. Time series rainfall spike modelling from Markov chains and queueing theory approach for rainfall attenuation over terrestrial and earth-space radio wave propagation in Jimma, Ethiopia. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; pp. 4991–4995.
Al-Samman, A.M.; Mohamed, M.; Ai, Y.; Cheffena, M.; Azmi, M.H.; Rahman, T.A. Rain Attenuation Measurements and Analysis at 73 GHz E-Band Link in Tropical Region. IEEE Commun. Lett. 2020, 24, 1368–1372.
Diba, F.; Afullo, T.; Alonge, A. Rainfall rate and attenuation performance analysis at microwave and millimeter bands for the design of terrestrial line-of-sight radio links in Ethiopia. SAIEE Afr. Res. J. 2016, 107, 177–186.
Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579.
Luini, L.; Capsoni, C. MultiEXCELL: A new rain field model for propagation applications. IEEE Trans. Antennas Propag. 2011, 59, 4286–4300.
Korai, U.A.; Luini, L.; Nebuloni, R. Model for the prediction of rain attenuation affecting free space optical links. Electronics 2018, 7, 407.
Wen, G.; Fox, N.I.; Market, P.S. The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty. Remote Sens. 2020, 12, 1072.
Das, D.; Maitra, A. Time series prediction of rain attenuation from rain rate measurement using synthetic storm technique for a tropical location. AEU-Int. J. Electron. Commun. 2014, 68, 33–36.
Kanellopoulos, S.A.; Panagopoulos, A.D.; Kourogiorgas, C.I.; Kanellopoulos, J.D. Satellite and terrestrial links rain attenuation time series generator for heavy rain climatic regions. IEEE Trans. Antennas Propag. 2013, 61, 3396–3399.
Liu, J.; Matolak, D.W. Worst Month Tropospheric Attenuation Variability Analysis: ITU Model vs. Rain Gauge Data for Air-Satellite Links. In Proceedings of the 2018 11th Global Symposium on Millimeter Waves (GSMM), Boulder, CO, USA, 22–24 May 2018; IEEE: Boulder, CO, USA, USA, 2018; pp. 1–5.
National Oceanic and Atmospheric Administration (NOAA). National Climatic Data Center; HeinOnline: Buffalo, NY, USA, 2014.
ITU-R Recommendations. Specific Attenuation Model for Rain for Use in Prediction Methods; Recommendation ITU-R P. 838-3; ITU-R Recommendations: Geneva, Switzerland, 2005.
Nandi, D.D.; Pérez-Fontán, F.; Pastoriza-Santos, V.; Machado, F. Application of synthetic storm technique for rain attenuation prediction at Ka and Q band for a temperate Location, Vigo, Spain. Adv. Space Res. 2020, 66, 800–809.
Luini, L.; Panzeri, A.; Riva, C. Enhancement of the Synthetic Storm Technique for the Prediction of Rain Attenuation Time Series at EHF. IEEE Trans. Antennas Propag. 2020.
Kourogiorgas, C.; Kelmendi, A.; Panagopoulos, A.D.; Livieratos, S.N.; Vilhar, A.; Chatzarakis, G.E. Rain attenuation time series synthesizer based on copula functions. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–4.
Andrade, F.J.; da Silva Mello, L.A. Rain attenuation time series synthesizer based on the gamma distribution. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1381–1384.
Boulanger, X.; Feral, L.; Castanet, L.; Jeannin, N.; Carrie, G.; Lacoste, F. A rain attenuation time-series synthesizer based on a dirac and lognormal distribution. IEEE Trans. Antennas Propag. 2013, 61, 1396–1406.
Kourogiorgas, C.; Panagopoulos, A.; Livieratos, S.; Chatzarakis, G. Rain attenuation time series synthesizer based on inverse Gaussian distribution. Electron. Lett. 2015, 51, 2162–2164.
Nebuloni, R.; Capsoni, C.; Luccini, M. Advanced time series synthesizer for simulation of joint rain attenuation conditions. Radio Sci. 2014, 49, 699–708.
Xie, P.; Chen, M.; Yang, S.; Yatagai, A.; Hayasaka, T.; Fukushima, Y.; Liu, C. A gauge-based analysis of daily precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607–626.
Shi, J.; Yuan, F.; Shi, C.; Zhao, C.; Zhang, L.; Ren, L.; Zhu, Y.; Jiang, S.; Liu, Y. Statistical Evaluation of the Latest GPM-Era IMERG and GSMaP Satellite Precipitation Products in the Yellow River Source Region. Water 2020, 12, 1006.
Jing, W.; Song, J.; Zhao, X. Validation of ECMWF Multi-Layer Reanalysis Soil Moisture Based on the OzNet Hydrology Network. Water 2018, 10, 1123.
Yang, G.; Ndzi, D.L.; Gremont, B.C.; Paulson, K.; Filip, M.; Al-Hassani, A.H. The impact of spatial–temporal averaging on the dynamic-statistical properties of rain fields. IEEE Trans. Antennas Propag. 2019, 67, 7505–7517.
Goddard, J.; Thurai, M. Radar-derived path reduction factors for terrestrial systems. In Proceedings of the Tenth International Conference on Antennas and Propagation (Conf. Publ. No. 436), Edinburgh, UK, 14–17 April 1997; IET: Edinburgh, UK, 1997; Volume 2, pp. 218–221.
Lin, S. 11-GHz radio: Nationwide long-term rain rate statistics and empirical calculation of 11-GHz microwave rain attenuation. Bell Syst. Tech. J. 1977, 56, 1581–1604.
Khamis, N.H.H.; Din, J.; Rahman, T.A. Derivation of path reduction factor from the Malaysian meteorological radar data. In Proceedings of the 2005 1st International Conference on Computers, Communications & Signal Processing with Special Track on Biomedical Engineering, Kuala Lumpur, Malaysia, 14–16 November 2005; pp. 207–210.
Mello, L.D.S.; Pontes, M.; De Souza, R.; Garcia, N.P. Prediction of rain attenuation in terrestrial links using full rainfall rate distribution. Electron. Lett. 2007, 43, 1442–1443.
Moupfouma, F. Electromagnetic waves attenuation due to rain: A prediction model for terrestrial or LOS SHF and EHF radio communication links. J. Infrared Millim. Terahertz Waves 2009, 30, 622–632.
Sharma, P.; Hudiara, I.; Singh, M. Measurement of rain induced attenuation over a line of sight link operating at 28.75 GHz at Amritsar (INDIA). J. Infrared Millim. Terahertz Waves 2009, 30, 908–914.
Abdulrahman, A.; Rahman, T.; Rahim, S.; Islam, M.U. Empirically derived path reduction factor for terrestrial microwave links operating at 15 GHz in Peninsula Malaysia. J. Electromagn. Waves Appl. 2011, 25, 23–37.
Akuon, P.O.; Afullo, T. Path reduction factor modeling for terrestrial links based on rain cell growth. In Proceedings of the IEEE Africon’11, Livingstone, Zambia, 13–15 September 2011; pp. 1–6.
Ghiani, R.; Luini, L.; Fanti, A. Investigation of the path reduction factor on terrestrial links for the development of a physically-based rain attenuation model. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–2.
ITU-R Recommendations. Prediction Methods Required for the Design of Terrestrial Line-of-Sight Systems, Document ITU-R P. 530-17; International Telecommunication Union Radiocommunication Recommendations; ITU-R Recommendations: Geneva, Switzerland, 2017.
Kang, W.G.; Kim, T.H.; Park, S.W.; Lee, I.Y.; Pack, J.K. Modeling of Effective Path-Length Based on Rain Cell Statistics for Total Attenuation Prediction in Satellite Link. IEEE Commun. Lett. 2018, 22, 2483–2486.
Budalal, A.A.H.; Islam, R.M.; Abdullah, K.; Rahman, T.A. Modification of Distance Factor in Rain Attenuation Prediction for Short Range Millimetre-wave Links. IEEE Antennas Wirel. Propag. Lett. 2020.
Paulson, K.S.; Ranatunga, C.; Bellerby, T. A method to estimate trends in distributions of 1 min rain rates from numerical weather prediction data. Radio Sci. 2015, 50, 931–940.
Singh, R.; Acharya, R. Development of a new global model for estimating one-minute rainfall rate. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6462–6468.
Oh, S.B.; Kollias, P.; Lee, J.S.; Lee, S.W.; Lee, Y.H.; Jeong, J.H. Rain-rate estimation algorithm using signal attenuation of Ka-band cloud radar. Meteorol. Appl. 2020, 27, e1825.
Ostrometzky, J.; Eshel, A. Empirical study of the quantization induced bias in commercial microwave links’ min/max attenuation measurements for rain monitoring. Environments 2018, 5, 80.
Hewage, P.; Trovati, M.; Pereira, E.; Behera, A. Deep learning-based effective fine-grained weather forecasting model. Pattern Anal. Appl. 2020, 24, 343–366.
Kashiwao, T.; Nakayama, K.; Ando, S.; Ikeda, K.; Lee, M.; Bahadori, A. A neural network-based local rainfall prediction system using meteorological data on the Internet: A case study using data from the Japan Meteorological Agency. Appl. Soft Comput. 2017, 56, 317–330.
Cramer, S.; Kampouridis, M.; Freitas, A.A.; Alexandridis, A.K. An extensive evaluation of seven machine learning methods for rainfall prediction in weather derivatives. Expert Syst. Appl. 2017, 85, 169–181.
Tran Anh, D.; Duc Dang, T.; Pham Van, S. Improved rainfall prediction using combined pre-processing methods and feed-forward neural networks. J. Multidisciplinary Sci. J. 2019, 2, 65–83.
Giro, R.A.; Luini, L.; Riva, C.G. Rainfall Estimation from Tropospheric Attenuation Affecting Satellite Links. Information 2020, 11, 11.
Xian, M.; Liu, X.; Yin, M.; Song, K.; Zhao, S.; Gao, T. Rainfall Monitoring Based on Machine Learning by Earth-Space Link in the Ku Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3656–3668.
Han, C.; Huo, J.; Gao, Q.; Su, G.; Wang, H. Rainfall Monitoring Based on Next-Generation Millimeter-Wave Backhaul Technologies in a Dense Urban Environment. Remote Sens. 2020, 12, 1045.
Olsen, R.; Rogers, D.V.; Hodge, D. The aRb relation in the calculation of rain attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329.
de Bettencourt, J. Statistics of terrestrial millimeter-wave rainfall attenuation. In IUCRM Colloquium on the Fine Scale Structure of Precipitation and EM Propagation; AGU: Washington, DC, USA, 1973.
Perić, M.V.; Perić, D.B.; Todorović, B.M.; Popović, M.V. Dynamic rain attenuation model for millimeter wave network analysis. IEEE Trans. Wirel. Commun. 2016, 16, 441–450.
Garcia-Lopez, J.; Casares-Giner, V. Modified Lin’s empirical formula for calculating rain attenuation on a terrestrial path. Electron. Lett. 1981, 17, 34–36.
Da Silva Mello, L.A.; Pontes, M.S. Improved unified method for the prediction of rain attenuation in terrestrial and earth space links. In Proceedings of the 2009 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Belem, Brazil, 3–6 November 2009; pp. 569–573.
Mello, L.; Pontes, M.S. Unified method for the prediction of rain attenuation in satellite and terrestrial links. J. Microw. Optoelectron. Electromagn. Appl. 2012, 11, 1–14.
Abdulrahman, A.; Rahman, T.A.; Rahim, S.K.A.; Islam, M.R.; Abdulrahman, M. Rain attenuation predictions on terrestrial radio links: Differential equations approach. Trans. Emerg. Telecommun. Technol. 2012, 23, 293–301.
Crane, R.K. Prediction of attenuation by rain. IEEE Trans. Commun. 1980, 28, 1717–1733.
Crane, R.K. A two-component rain model for the prediction of attenuation statistics. Radio Sci. 1982, 17, 1371–1387.
Ghiani, R.; Luini, L.; Fanti, A. A physically based rain attenuation model for terrestrial links. Radio Sci. 2017, 52, 972–980.
Capsoni, C.; Fedi, F.; Paraboni, A. A comprehensive meteorologically oriented methodology for the prediction of wave propagation parameters in telecommunication applications beyond 10 GHz. Radio Sci. 1987, 22, 387–393.
Féral, L.; Sauvageot, H.; Castanet, L.; Lemorton, J. HYCELL—A new hybrid model of the rain horizontal distribution for propagation studies: 1. Modeling of the rain cell. Radio Sci. 2003, 38.
Ghanim, M.; Alhilali, M.; Din, J.; Lam, H.Y. Rain attenuation statistics over 5G millimetre wave links in Malaysia. Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 1012–1017.
Singh, H.; Kumar, V.; Saxena, K.; Boncho, B.; Prasad, R. Proposed Model for Radio Wave Attenuation due to Rain (RWAR). Wirel. Pers. Commun. 2020, 115, 791–807.
Kestwal, M.C.; Joshi, S.; Garia, L.S. Prediction of Rain Attenuation and Impact of Rain in Wave Propagation at Microwave Frequency for Tropical Region (Uttarakhand, India). Int. J. Microw. Sci. Technol. 2014, 2014, 1–6.
Andrade, F.J.; de Medeiros, Á.A.; da Silva Mello, L.A. Short-term rain attenuation predictor for terrestrial links in tropical area. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 1325–1328.
Develi, I. Differential evolution based prediction of rain attenuation over a LOS terrestrial link situated in the southern United Kingdom. Radio Sci. 2007, 42, 1–6.
Livieratos, S.N.; Cottis, P.G. Rain Attenuation Along Terrestrial Millimeter Wave Links: A New Prediction Method Based on Supervised Machine Learning. IEEE Access 2019, 7, 138745–138756.
Pinto-Mangones, A.D.; Torres-Tovio, J.M.; Pérez-García, N.A.; da Silva Mello, L.A.; Ruiz-Garcés, A.F.; León-Acurio, J. Improved ITU Model for Rainfall Attenuation Prediction of in Terrestrial Links. In Proceedings of the International Conference on Advances in Emerging Trends and Technologies, Guayaquil, Ecuador, 27–29 March 2019; Springer: Guayaquil, Ecuador, 2019; pp. 531–541.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.