2.1. Molecular Dynamics Simulations

Molecular dynamics (MD) simulation is a well-established technique used for the study of various chemical substances and mixtures in any state of matter and almost at any temperature and pressure conditions ^{[2][3][4][5][6]}. MD is sometimes described as “computational molecular microscope”, while in fact, MD is more than just an in silico microscope as it can be used to determine not only structural but also energetic and thermodynamic properties ^[7], as well as to improve the accuracy of NMR parameters calculations, which is discussed in the next section.

Molecular dynamics methods, regardless of the objects being modeled and the method being used, are, in their basic assumptions, similar. The simulation starts with an initial configuration of the system and energy minimization through the optimization of the positions of all atoms ^[8]. Subsequently, the forces acting on each atom are then calculated and used in equations of motion to update the configuration. This process is repeated to generate a trajectory—a contiguous set of configurations obtained during the time evolution of a studied system.

One of the most challenging aspects of MD simulations is the calculation of the interatomic forces. In classical molecular mechanics-based simulations, they are computed from empirical potential functions, which have been previously parameterized to reproduce experimental or accurate ab initio data of small model systems ^[9]. Even though these empirical potentials have been created with great effort to be as accurate as possible, usually the transferability to systems or regions of the phase diagram different from the ones to which they have been fitted is restricted and may lead to significant inaccuracy ^[10]. Moreover, some of the most important and interesting phenomena of modern physics and chemistry are intrinsically nonclassical but quantum ^[11]. Therefore, a first-principles-based approach, such as aiMD, where the forces are calculated on-the-fly from accurate electronics structure calculations, is very attractive as many of these limitations can be removed. However, the increased accuracy and predictive power of such simulations comes at a significant computational cost that was, for a long time, not affordable for most researchers. For this reason, density functional theory (DFT) is so far the most commonly employed electronic structure theory in the context of aiMD. However, it is important to note that aiMD is a general concept that can be used in conjunction with any electronic structure method ^[12].

2.2. Ab Initio Molecular Dynamics (aiMD)

In almost every method of molecular modeling, in order to reduce the computational complexity and in consequence the time of calculations and hardware requirements, some approximations must be applied, while maintaining the predictive accuracy. In the field of aiMD, there are two most commonly used approximations. The first one, called the adiabatic approximation, assumes that the electronic wave functions adapt quasi-instantaneously to a variation of the nuclear configuration. The second one, named the Born–Oppenheimer approximation, assumes that the electronic and the nuclear motions are separable due to the significant difference between nuclear and electronic masses ^[13].

Two of the most commonly used methods of aiMD simulations in the studies combined with NMR parameters calculations are the Born–Oppenheimer (BO) MD ^[14] simulations—in which the forces at each timestep are calculated quantum mechanically and the classical Newtonian equations of motion are being solved—and the ab initio Car–Parrinello (CP) MD ^[15] simulations, where quantum mechanical calculations are performed at each step of the simulation to solve the Car–Parrinello equations of motion. However, in the literature, the examples of successful applications of more computationally demanding Path integral MD (PIMD) ^[16] simulations can be found, as well.

In BOMD, it is assumed that the adiabatic and the Born–Oppenheimer approximations are valid and that the nuclei follow a semi-classical Newton equation whose potential is determined by the Ehrenfest theorem. It is further postulated that the electronic wave function is in its ground state, implying the lowest energy. In Born-Oppenheimer MD (BOMD), the potential energy is minimized at every MD step. Nevertheless, due to the inclusion of the BO approximation, the electronic and nuclear subsystems are fully decoupled from each other. Due to the adiabatic separation, there are no additional restrictions on the maximum permissible integration time step, which hence can be chosen up to the nuclear resonance limit.

In CPMD, a coupled electron-ion dynamics is performed, wherein the electronic degrees of freedom are added to the Lagrangian as classical ones. At variance to BOMD, the computational cost to compute the nuclear forces in each aiMD step is now much reduced since no SCF (Self-Consistent Field) cycle is required to ensure that they are consistent with the instantaneous energy, and to force the electrons to adiabatically follow the nuclei. However, in the CPMD, the required time step is usually significantly shorter than in BOMD, which increases the computational time of CPMD simulation. An analysis of previously reported studies shows that it is very hard to unambiguously determine if either BOMD or CPMD is to favor. The differences between the results obtained using those two methods are often rather subtle and depend largely on the particular application (Figure 1).

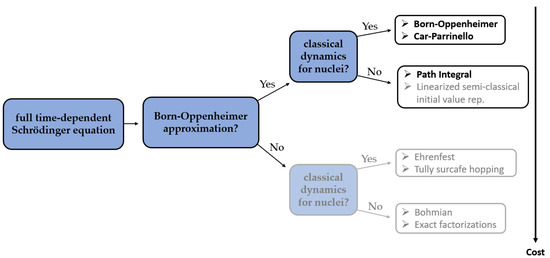
Figure 1. The major differences between the methods of aiMD simulations ^[17]. Bolded methods have already found their application in combination with NMR parameters calculations.

The ab initio path integral technique is based on the formulation of quantum statistical mechanics in terms of Feynman path integrals. Contrarily to the previous approaches, the path integral molecular dynamics (PIMD) allows for a quantum formulation which includes, in addition to the electronic degrees of freedom, their nuclear counterpart. Such an approach is therefore recognized to be more accurate than BOMD or CPMD, especially for systems containing light nuclei. Unfortunately, conventional PIMD simulations require a considerable computational cost, which is the reason why they are not so popular in combination with NMR parameters calculations yet.

Integrating equations of motion allows the exploration of the constant-energy surface of a system. However, most natural phenomena occur under conditions where the system is exposed to external pressure or exchanges heat with the environment. Under these conditions, the total energy of the system is no longer conserved and extended forms of molecular dynamics are required ^[18][19].

Depending on which state variables (the energy E, number of particles N, pressure P, temperature T, and volume V) are kept fixed, different statistical ensembles can be generated. Microcanonical (NVE) ensemble in which the energy is conserved is the natural ensemble to simulate molecular dynamics. Canonical (NVT) ensemble requires the system to be in contact with a heat bath so that the states of the system will differ in total energy. Isothermic-Isobaric (NPT) ensemble is particularly interesting because most experiments are usually done at constant temperature and pressure, which enables more accurate modeling of conformational changes. Several methods are available for controlling temperature and pressure by means of thermostat and barostat algorithms ^[20][21].

2.3. Combining the aiMD and NMR Parameters Calculations

NMR spectroscopy is currently one of the basic tools for the structural analysis of various systems and is widely used in the studies of liquid, solid, and gas phases. In the experimental approach, the basic NMR parameter is the chemical shift (δ) characterizing the position of the resonance line in the NMR spectrum. From the physical description point of view, it is directly related to the shielding parameter (σ), described by a second order tensor. The position of the line in the NMR spectrum can be directly related to the isotropic value as determined by the trace of the tensor, but the individual components influence the shape of the lines. While in solution, due to the short correlation times, the screening parameters are averaged to the isotropic value; in the case of solid-state NMR measurements, the full tensor can be usually determined, which allows a deeper analysis of the molecular structure and interactions. The QM calculations methods allow to determine the full tensor and analyze not only the isotropic parameter, but also the individual components of the anisotropy tensor.

Another NMR parameter that can be obtained from NMR spectrum is the indirect spin-spin J coupling, which is highly dependent from molecular geometry and widely used in conformational analysis. For quadrupole nuclei (with spin I > ½), the additional quadrupole coupling has a strong influence on the position and shape of the signal line in the experimental NMR spectrum. All these parameters allow for a deep insight into the structure of molecular systems. The use of QM computational methods allows for the calculation of these parameters, which not only simplifies the analysis of NMR spectra, but also allows to translate the experimental parameters into structural aspects of the analyzed molecular system.

NMR shielding tensors may be computed using multiple methods, such as the Continuous Set of Gauge Transformations (CSGT) ^[22], Gauge-Independent Atomic Orbital (GIAO) ^[23], Individual Gauges for Atoms In Molecules (IGAIM, a slight variation on the CSGT method) ^[24], Single Origin (SO), or Gauge Including Projector Augmented Wave (GIPAW) ^[25]. The similarities and differences of these approaches are not discussed in this review so as not to stray from the main topic. Such quantum chemical calculations are typically performed using static, optimized structures at 0 K, and thus neglecting zero-point motion and not accounting for the thermal dynamics, which can lead to significant discrepancies between computed and experimental data. This is particularly visible in solutions, where the configurations of neighboring molecules change dynamically, resulting in the dynamic changes of the intermolecular contributions to shielding. Therefore, dynamic averaging should be taken into account, even when there are no significant strong intermolecular interactions.

In order to somehow correct the computational results to include the effects of dynamics, various scaling methods have been proposed. For example, chemical shift anisotropies have often been found to be overestimated by DFT calculations, and several scaling factors ranging from 0.76 to 0.95 ^[26][27] and depending on the studied structures have been proposed. Such an approach may be quick and easy to implement, but if the discrepancies between calculated and experimental data result at least partially from the neglect of the dynamics in the calculations, then applying such scaling factors removes potential information about dynamics. Therefore, understanding how vibrational motions affect NMR tensor parameters may lead not only to a better agreement with experiment, but also to a proper description of the dynamics in the studied systems. It is not surprising, then, that the number of successful and non-routine studies combining aiMD and NMR parameters calculations is increasing constantly; to prove this statement, some of them are discussed in more detail in the next section.